阅读量:4
二分查找是一种在有序数组中查找特定元素的搜索算法。搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且同样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。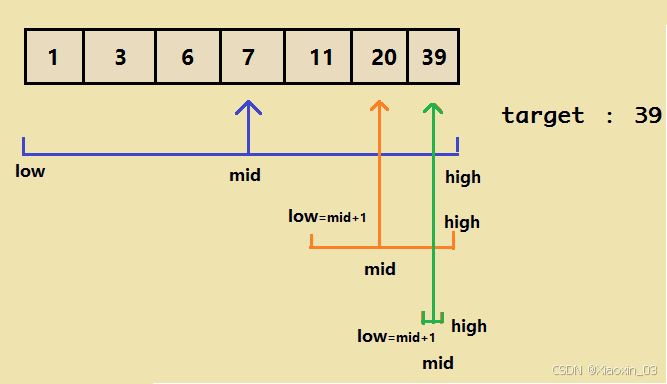
引言
在计算机科学中，二分查找（Binary Search）是一种高效的查找算法，尤其适用于已排序的数组。相比于线性查找，二分查找的时间复杂度要低得多，为O(log n)，这使得它在大数据集中的应用非常广泛。本文将详细介绍二分查找的基本原理，并提供多种编程语言的实现示例。
参考文献
"A Comparison of Sorting Algorithms for the Alpha 21164" - 这篇论文虽然主要关注排序算法，但也讨论了二分查找算法在搜索已排序数据集中的效率。
"The Art of Computer Programming, Volume 3: Sorting and Searching" - 唐纳德·克努特的著作，详细介绍了二分查找和其他搜索算法。"Data Structures and Algorithm Analysis in C++" by Mark Allen Weiss - 这本书涵盖了包括二分查找在内的多种数据结构和算法。
二分查找算法详解
假设我们有一个升序排列的数组arr和一个目标值target，我们的目标是在arr中找到target的位置。算法步骤如下：
缺点
与其他算法的比较
与线性搜索相比，二分查找在有序数据集上的性能显著更优，但线性搜索无需数据排序，适用于无序或动态数据。与哈希查找相比，虽然哈希查找在理想情况下可以达到O(1)的查找效率，但它需要额外的存储空间来构建哈希表，并且不能保证无冲突。
应用案例
二分查找在多个领域都有广泛的应用：
- 初始化两个指针
left和right，分别指向数组的第一个元素和最后一个元素。 - 当
left <= right时，执行循环：- 计算中间位置
mid = (left + right) // 2。 - 如果
![arr[mid] == target](/zb_users/upload/2024/csdn/eq.png)
mid。 - 如果
left设置为mid + 1。 - 如果
right设置为mid - 1。
- 计算中间位置
- 如果没有找到目标值，返回
-1表示未找到。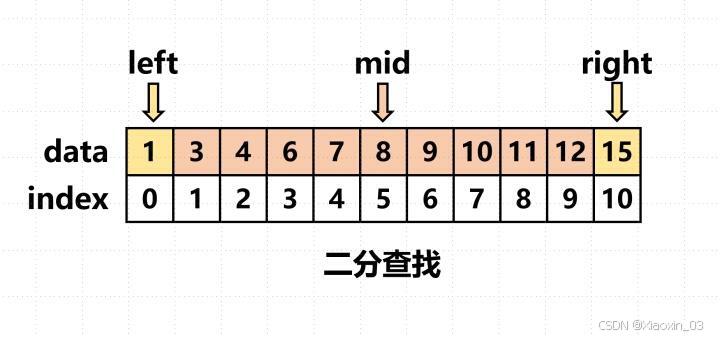
实现代码
下面我们将用Python和JavaScript两种语言来实现二分查找算法。
Python 实现
def binary_search(arr, target): left, right = 0, len(arr) - 1 while left <= right: mid = (left + right) // 2 if arr[mid] == target: return mid elif arr[mid] < target: left = mid + 1 else: right = mid - 1 return -1 # 测试代码 arr = [1, 3, 5, 7, 9, 11] target = 7 print(binary_search(arr, target)) # 输出: 3JavaScript 实现
function binarySearch(arr, target) { let left = 0; let right = arr.length - 1; while (left <= right) { const mid = Math.floor((left + right) / 2); if (arr[mid] === target) { return mid; } else if (arr[mid] < target) { left = mid + 1; } else { right = mid - 1; } } return -1; } // 测试代码 const arr = [1, 3, 5, 7, 9, 11]; const target = 7; console.log(binarySearch(arr, target)); // 输出: 3扩展 二分查找的变体与高级应用
旋转数组的二分查找
在标准的二分查找中，数组是单调递增的。但在一些场景下，数组可能是经过旋转的，即数组的一部分被移动到了数组的另一端。例如，[3, 4, 5, 1, 2] 就是一个经过旋转的有序数组。在这种情况下，我们如何进行有效的二分查找呢？
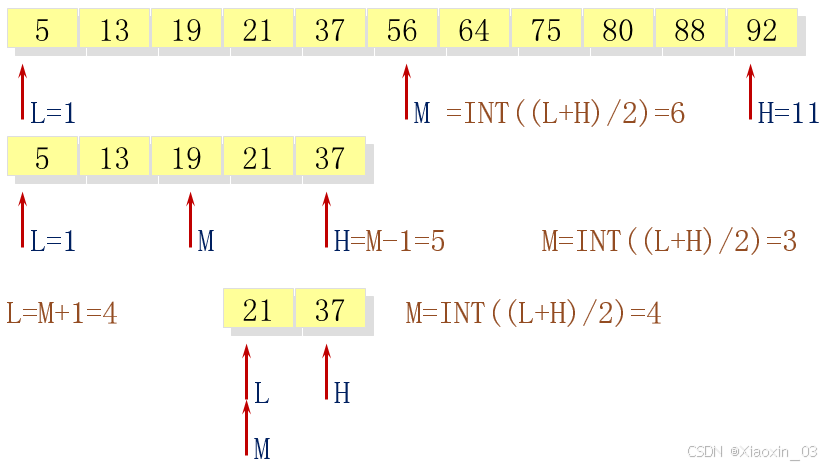
Python 实现
def rotated_binary_search(arr, target): left, right = 0, len(arr) - 1 while left <= right: mid = (left + right) // 2 if arr[mid] == target: return mid # 判断哪一边是有序的 if arr[left] <= arr[mid]: # 左边是有序的 if arr[left] <= target < arr[mid]: right = mid - 1 else: left = mid + 1 else: # 右边是有序的 if arr[mid] < target <= arr[right]: left = mid + 1 else: right = mid - 1 return -1 # 测试代码 arr = [4, 5, 6, 7, 0, 1, 2] target = 0 print(rotated_binary_search(arr, target)) # 输出: 42. 寻找最接近的元素
有时我们可能需要在数组中找到最接近给定目标值的元素。这可以通过稍微修改二分查找算法来实现。
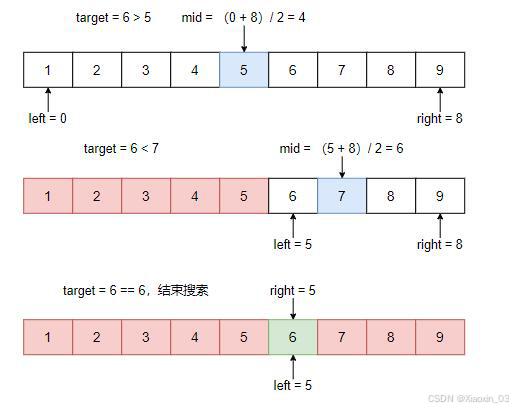
Python 实现
def find_closest(arr, target): left, right = 0, len(arr) - 1 closest = None while left <= right: mid = (left + right) // 2 if arr[mid] == target: return arr[mid] if closest is None or abs(target - arr[mid]) < abs(target - closest): closest = arr[mid] if arr[mid] < target: left = mid + 1 else: right = mid - 1 return closest # 测试代码 arr = [1, 2, 3, 4, 5] target = 3.5 print(find_closest(arr, target)) # 输出: 3 或 4，取决于具体实现3. 多次出现的元素查找
当数组中有重复的元素时，我们可能需要找到第一个或最后一个出现的指定元素。
Python 实现
def find_first_occurrence(arr, target): left, right = 0, len(arr) - 1 result = -1 while left <= right: mid = (left + right) // 2 if arr[mid] == target: result = mid right = mid - 1 # 继续向左查找 elif arr[mid] < target: left = mid + 1 else: right = mid - 1 return result # 测试代码 arr = [1, 2, 2, 2, 3, 4, 5] target = 2 print(find_first_occurrence(arr, target)) # 输出: 1优势与缺点
优势
高效性：二分查找的时间复杂度为O(log n)，这意味着即使在非常大的数据集中，算法也能迅速定位目标元素。相比之下，线性搜索的时间复杂度为O(n)，在数据量庞大时效率低下。
低比较次数：二分查找每次迭代都将搜索空间减半，因此所需的比较次数远低于线性搜索。
稳定性能：在平均和最坏情况下，二分查找都表现出色，不会像某些其他算法那样在特定输入下性能显著下降。
有序性要求：二分查找依赖于数据的有序性。如果数据无序，需要先进行排序，这会增加额外的时间成本。
插入与删除困难：在有序数组中进行插入或删除操作时，可能需要移动大量元素，影响效率。
空间限制：二分查找最适合静态数据结构，如数组。在链表等动态数据结构上，由于随机访问的限制，其效率会大打折扣。
数据库索引：数据库系统利用类似于二分查找的策略在索引上快速定位记录，极大提高了查询速度。
编译器：在编译过程中，二分查找用于在符号表中快速查找变量和函数。
游戏开发：在游戏引擎中，二分查找用于快速查找碰撞检测、地图数据检索等。
数据挖掘与机器学习：在特征选择和模型训练中，二分查找可用于优化参数寻优。
