队列(Queue)是一种特殊的线性数据结构,它遵循FIFO(First In First Out,先入先出)的原则。队列只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作。队列中没有元素时,称为空队列。
队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队,从队列中删除一个队列元素称为出队。因为队列只允许在一端插入,在另一端删除,所以又称为先进先出(FIFO—first in first out)线性表,简称队列。
在程序中,队列常常被用来处理需要按一定顺序处理的任务,例如打印任务队列、线程任务调度等。此外,队列也在许多算法中发挥着重要作用,如广度优先搜索(BFS)等。
队列的实现方式有多种,包括基于数组的静态队列、基于链表的动态队列等。在实际应用中,可以根据具体需求选择合适的队列实现方式。
队列的主要特点包括:
先进先出:队列中的元素按照进入队列的先后顺序依次出队。
操作受限:队列只允许在队尾插入元素(入队),在队头删除元素(出队),其他位置的元素无法直接访问或修改。
有序性:由于遵循FIFO原则,队列中的元素始终保持一定的顺序。
队列的链式存储结构为:
typedef int QDataType; // 链式结构:表示队列 typedef struct QListNode { struct QListNode* next; QDataType data; }QNode; // 队列的结构 typedef struct Queue { QNode* front; QNode* rear; int size; }Queue; 队列的顺序存储结构为:
#define MAXQSIZE 100 //队列可能达到的最大长度 typedef struct { QElemType* base; //存储空间的基地址 int front; //头指针 int rear; //尾指针 }SqQueue; 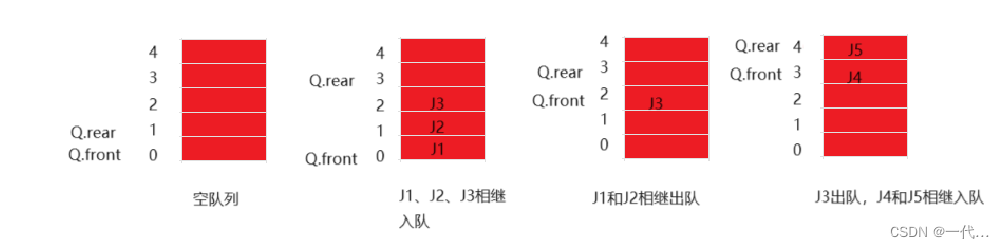
假设当前队列分配的空间最大为6,则当队列处于上图的最后一个状态时,就不可以在继续插入新的队尾元素,否则会出现溢出的情况,即因数组越界而导致程序的非法操作错误。但是队列的实际空间并未占满,这种现象就被称为假溢出。
那么怎么解决这个问题呢?
我们就可以运用一个较为巧妙的方法:循环队列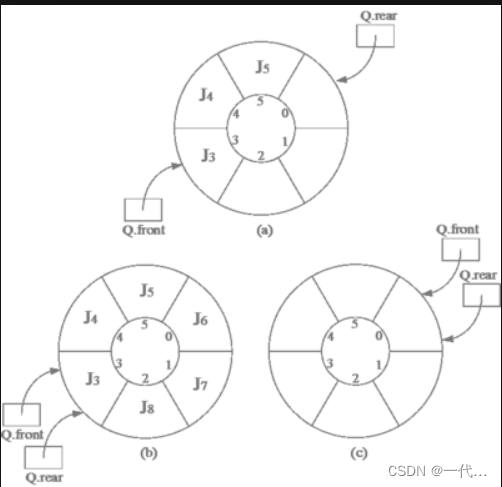
但这里我们面临一个问题,就是front==rear的时候时队空还是队满
可以发现并不好来判断
下面我们就有两种方法来解决下列问题
| 多开辟用一个空间(即少用一个元素空间),假设队列的空间为k+1,但当有m个元素的时候就认为时队满 | |
|---|---|
| 即(Q.rear + 1)%(k+1) == Q.front即为队满,Q.rear == Q.front时为队空 | |
| 用一个标志位来Size判断队列是空还是队满 | |
| 即当Size == k时为队满,Size == 0时为队空 | – |
下面我们就用一种方法来实现循环队列
结构体定义:
typedef int QDataType; typedef struct { QDataType* a; int front;//指向头 int rear;//指向尾的下一位 int k;//队列的长度 } MyCircularQueue; 创建队列
MyCircularQueue* myCircularQueueCreate(int k) { MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue)); //开辟一个大小为(k+1)的数组空间,多开一个空间以便判断队列为空还是满的 //防止假溢出现象 obj->a = (QDataType*)malloc((k + 1) * sizeof(QDataType)); obj->k = k; obj->front = obj->rear = 0; return obj; } 判断队空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) { return obj->rear == obj->front; } 判断队满
bool myCircularQueueIsFull(MyCircularQueue* obj) { return (obj->rear + 1) % (obj->k + 1) == obj->front; } 入队
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) { if (myCircularQueueIsFull(obj)) { return false; } obj->a[obj->rear] = value; obj->rear++; obj->rear %= obj->k + 1; return true; } 出队
bool myCircularQueueDeQueue(MyCircularQueue* obj) { if (myCircularQueueIsEmpty(obj)) { return false; } obj->front++; obj->front %= obj->k + 1; return true; } 取出队头元素
int myCircularQueueFront(MyCircularQueue* obj) { if (myCircularQueueIsEmpty(obj)) return -1; else return obj->a[obj->front]; } 取出队尾元素
int myCircularQueueRear(MyCircularQueue* obj) { if (myCircularQueueIsEmpty(obj)) return -1; else return obj->a[(obj->rear - 1 + obj->k + 1) % (obj->k + 1)]; } 销毁队列
void myCircularQueueFree(MyCircularQueue* obj) { free(obj->a); free(obj); } 