꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页:xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客系列专栏:机器学习系列专栏
"探索未来,掌握人工智能"🚀 点击加入我们的AI学习之旅,让技术变得有趣又易懂,点击跳转
我的目标:"团团等我💪( ◡̀_◡́ ҂)"( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝+关注(互三必回)!
目录
二深度Q网络(Deep Q-Networks, DQN)解决序列决策问题

一.AI序列决策问题
AI序列决策问题是指在人工智能领域中,智能体需要在一个序列的环境中做出一系列决策,以达到某个目标或最大化某种累积奖励的问题。这类问题通常涉及到强化学习,其中智能体通过与环境的交互来学习最优的行为策略。
1.序列决策问题的特点:
时间维度:决策不是一次性的,而是需要在一系列时间步骤中进行。每个决策都会影响后续的状态和可能的决策。
状态变化:智能体的每个决策都会使环境从一个状态转移到另一个状态。状态可以是环境的描述,如游戏的当前分数、机器人的位置等。
奖励反馈:智能体在每个时间步骤做出决策后,环境会提供一个奖励(或惩罚),这是对智能体决策好坏的反馈。
长期目标:智能体的目标通常是长期的,比如最大化累积奖励、达到最终的胜利状态或完成任务。
不确定性:智能体在做出决策时可能无法完全了解环境的全部特性,因此需要在不确定性中做出最优的选择。
2.解决序列决策问题的AI方法:
强化学习:通过智能体与环境的交互来学习最优策略。智能体通过尝试不同的行动并接收环境的奖励或惩罚来学习。
动态规划:一种基于模型的优化方法,通过预测未来的状态和奖励来计算当前行动的价值。
蒙特卡洛方法:通过随机模拟来估计行动的价值,适用于难以精确建模的环境。
时序差分学习:结合了动态规划和蒙特卡洛方法的特点,通过学习状态和行动之间的差异来更新价值估计。
深度学习:使用深度神经网络来近似复杂的价值函数或策略函数,尤其在状态空间高维且连续时表现出色。
3.序列决策问题的应用场景:
- 游戏AI:如棋类游戏、电子游戏等,智能体需要通过一系列行动来赢得比赛。
- 机器人控制:机器人需要根据环境的变化做出连续的移动和操作决策。
- 自动驾驶汽车:汽车需要根据路况和交通规则做出连续的驾驶决策。
- 资源管理:如电网管理、网络带宽分配等,需要根据实时数据做出一系列调度决策。
AI序列决策问题是人工智能中一个非常重要且活跃的研究领域,它不仅挑战着智能体在复杂环境中的学习能力,也推动了AI技术在多个领域的应用和发展。
二深度Q网络(Deep Q-Networks, DQN)解决序列决策问题

1.什么是DQN
DQN属于DRL(深度强化学习)的一种,它是深度学习与Q学习的结合体。使用 Q-learning 因为采用S-A表格的局限性,当状态和行为的组合不可穷尽时,就无法通过查表的方式选取最优的Action了。这时候就该想到深度学习了,想通过深度学习找到最优解在很多情况下确实不太靠谱,但是找到一个无限逼近最优解的次优解,倒是没有问题的。因此DQN实际上,总体思路还是用的Q学习的思路,不过对于给定状态选取哪个动作所能得到的Q值,却是由一个深度神经网络来计算的了,其流程图如下:
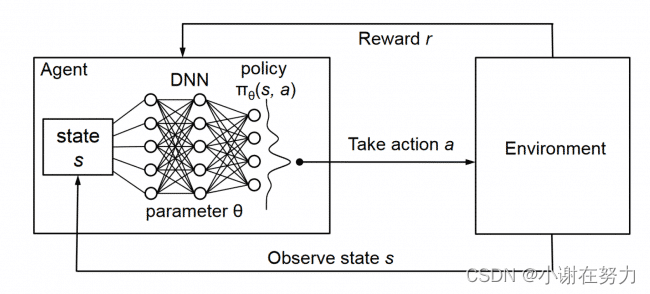
2.DNN如何训练
现在我们的选择哪个动作,是由DNN来做决定的,因此我们需要训练DNN以使其能达到令人满意的表现。这显然是一个监督学习的问题,那么训练集是什么,标签是什么,损失函数又是什么?
首先,我们DNN的输出值,自然是在给定状态的情况下,执行各action后能得到的Q值。然而事实上我们在很多情况下并不知道最优的Q值是什么,比如自动驾驶、围棋等情况,所以似乎我们没法给出标签。但是什么是不变的呢?Reward!
对状态s,执行动作a,那么得到的reward是一定的,而且是不变的!因此需要考虑从reward下手,让预测Q值和真实Q值的比较问题转换成让模型实质上在拟合reward的问题。
如果不能很好的理解,请看下面公式,下面公式中target是什么我们会在后面说到,这里先忽略它,那个红色的 θi- 我们也暂且将它当成 θi来看这个公式描述的就是模型的损失函数,大括号外面就是求一个均方差,我们主要看括号里面。前面被target标出来的地方是这一步得到的reward+下一状态所能得到的最大Q值,它们减去这一步的Q值,那么实际上它们的差就是实际reward减去现有模型认为在s下采取a时能得到的reward值。
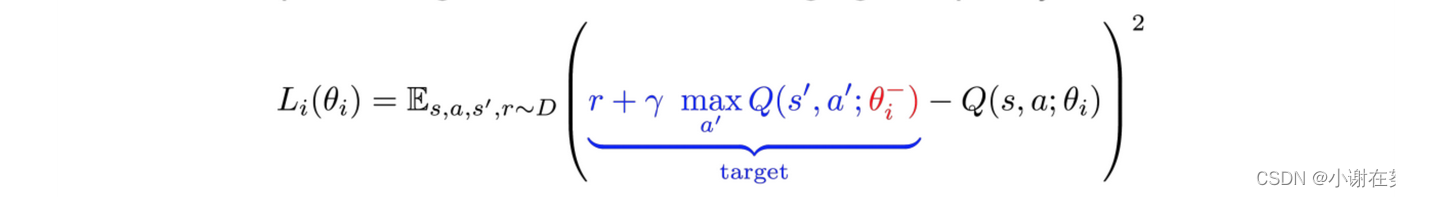
现在的问题就已经转换为需要一组训练集,它能够提供一批四元组(s, a, r, s’),其中s’为s执行a后的下一个状态。如果能有这样一个四元组,就能够用来训练DNN了,这就是我们要介绍的Experience reply。
Experience Reply
前面提到我们需要一批四元组(s, a, r, s’)来进行训练,因此我们需要缓存一批这样的四元组到经验池中以供训练之用。由于每次执行一个动作后都能转移到下一个状态,并获得一个reward,因此我们每执行一次动作后都可以获得一个这样的四元组,也可以将这个四元组直接放入经验池中。
我们知道这种四元组之间是存在关联性的,因为状态的转移是连续的,如果直接按顺序取一批四元组作为训练集,那么是容易过拟合的,因为训练样本间不是独立的!为解决这个问题,我们可以简单地从经验池中随机抽取少量四元组作为一个batch,这样既保证了训练样本是独立同分布的,也使得每个batch样本量不大,能加快训练速度。 训练的伪代码为:

Target Network
上面的代码似乎已经能够正常运行了,为什么又冒出一个target network呢?回想下前面那个公式,这里重新搬到下面来,是不是之前说target和θi-都先忽略,现在就解释一下为什么
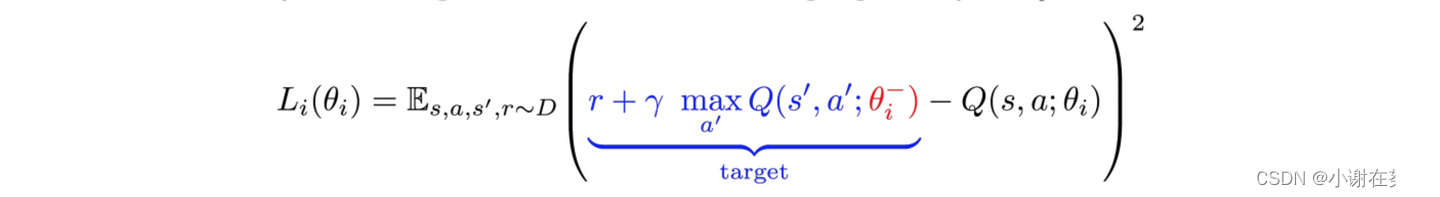
这个公式里θi-和θi肯定是有区别的,不然也不会使用两个符号了。事实上,我们需要设计两个DNN,它们结构完全一样,但是参数不一样,即神经网络中各层的权重、偏置等,一个的参数是θi-,而另一个是θi。我们每次迭代中,更新的是θi而不更新θi-,且规定每运行C步后让θi- = θi。而其θi-所在的网络就被称为target network。
为什么要弄这么奇怪的东西?
这也是为了防止过拟合。试想如果只有一个神经网络,那么它就在会不停地更新,那么它所追求的目标是在一直改变的,即在θ改变的时候,不止Q(s, a)变了,max Q(s’, a’)也变了。这样的好处是使得上面公式中target所标注的部分是暂时固定的,我们不断更新θ追逐的是一个固定的目标,而不是一直改变的目标。
如果做了这种考虑,那么伪代码就要做一点点修改了,修改后如下,大家可以对比着看:

三.Python实现DQN算法训练过程
在DQN中,Q值表中表示的是当前已学习到的经验。而根据公式计算出的 Q 值是agent通过与环境交互及自身的经验总结得到的一个分数(即:目标 Q 值)。最后使用目标 Q 值(target_q)去更新原来旧的 Q 值(q)。而目标 Q 值与旧的 Q 值的对应关系,正好是监督学习神经网络中结果值与输出值的对应关系。
所以,loss = (target_q - q)^2
即:整个训练过程其实就是 Q 值(q)向目标 Q 值(target_q)逼近的过程。

用TensorFlow实现的Deep Q-Network(DQN)的例子
import tensorflow as tf import numpy as np from collections import deque import random class DeepQNetwork: r = np.array([[-1, -1, -1, -1, 0, -1], [-1, -1, -1, 0, -1, 100.0], [-1, -1, -1, 0, -1, -1], [-1, 0, 0, -1, 0, -1], [0, -1, -1, 1, -1, 100], [-1, 0, -1, -1, 0, 100], ]) # 执行步数。 step_index = 0 # 状态数。 state_num = 6 # 动作数。 action_num = 6 # 训练之前观察多少步。 OBSERVE = 1000. # 选取的小批量训练样本数。 BATCH = 20 # epsilon 的最小值,当 epsilon 小于该值时,将不在随机选择行为。 FINAL_EPSILON = 0.0001 # epsilon 的初始值,epsilon 逐渐减小。 INITIAL_EPSILON = 0.1 # epsilon 衰减的总步数。 EXPLORE = 3000000. # 探索模式计数。 epsilon = 0 # 训练步数统计。 learn_step_counter = 0 # 学习率。 learning_rate = 0.001 # γ经验折损率。 gamma = 0.9 # 记忆上限。 memory_size = 5000 # 当前记忆数。 memory_counter = 0 # 保存观察到的执行过的行动的存储器,即:曾经经历过的记忆。 replay_memory_store = deque() # 生成一个状态矩阵(6 X 6),每一行代表一个状态。 state_list = None # 生成一个动作矩阵。 action_list = None # q_eval 网络。 q_eval_input = None action_input = None q_target = None q_eval = None predict = None loss = None train_op = None cost_his = None reward_action = None # tensorflow 会话。 session = None def __init__(self, learning_rate=0.001, gamma=0.9, memory_size=5000): self.learning_rate = learning_rate self.gamma = gamma self.memory_size = memory_size # 初始化成一个 6 X 6 的状态矩阵。 self.state_list = np.identity(self.state_num) # 初始化成一个 6 X 6 的动作矩阵。 self.action_list = np.identity(self.action_num) # 创建神经网络。 self.create_network() # 初始化 tensorflow 会话。 self.session = tf.InteractiveSession() # 初始化 tensorflow 参数。 self.session.run(tf.initialize_all_variables()) # 记录所有 loss 变化。 self.cost_his = [] def create_network(self): """ 创建神经网络。 :return: """ self.q_eval_input = tf.placeholder(shape=[None, self.state_num], dtype=tf.float32) self.action_input = tf.placeholder(shape=[None, self.action_num], dtype=tf.float32) self.q_target = tf.placeholder(shape=[None], dtype=tf.float32) neuro_layer_1 = 3 w1 = tf.Variable(tf.random_normal([self.state_num, neuro_layer_1])) b1 = tf.Variable(tf.zeros([1, neuro_layer_1]) + 0.1) l1 = tf.nn.relu(tf.matmul(self.q_eval_input, w1) + b1) w2 = tf.Variable(tf.random_normal([neuro_layer_1, self.action_num])) b2 = tf.Variable(tf.zeros([1, self.action_num]) + 0.1) self.q_eval = tf.matmul(l1, w2) + b2 # 取出当前动作的得分。 self.reward_action = tf.reduce_sum(tf.multiply(self.q_eval, self.action_input), reduction_indices=1) self.loss = tf.reduce_mean(tf.square((self.q_target - self.reward_action))) self.train_op = tf.train.GradientDescentOptimizer(self.learning_rate).minimize(self.loss) self.predict = tf.argmax(self.q_eval, 1) def select_action(self, state_index): """ 根据策略选择动作。 :param state_index: 当前状态。 :return: """ current_state = self.state_list[state_index:state_index + 1] if np.random.uniform() < self.epsilon: current_action_index = np.random.randint(0, self.action_num) else: actions_value = self.session.run(self.q_eval, feed_dict={self.q_eval_input: current_state}) action = np.argmax(actions_value) current_action_index = action # 开始训练后,在 epsilon 小于一定的值之前,将逐步减小 epsilon。 if self.step_index > self.OBSERVE and self.epsilon > self.FINAL_EPSILON: self.epsilon -= (self.INITIAL_EPSILON - self.FINAL_EPSILON) / self.EXPLORE return current_action_index def save_store(self, current_state_index, current_action_index, current_reward, next_state_index, done): """ 保存记忆。 :param current_state_index: 当前状态 index。 :param current_action_index: 动作 index。 :param current_reward: 奖励。 :param next_state_index: 下一个状态 index。 :param done: 是否结束。 :return: """ current_state = self.state_list[current_state_index:current_state_index + 1] current_action = self.action_list[current_action_index:current_action_index + 1] next_state = self.state_list[next_state_index:next_state_index + 1] # 记忆动作(当前状态, 当前执行的动作, 当前动作的得分,下一个状态)。 self.replay_memory_store.append(( current_state, current_action, current_reward, next_state, done)) # 如果超过记忆的容量,则将最久远的记忆移除。 if len(self.replay_memory_store) > self.memory_size: self.replay_memory_store.popleft() self.memory_counter += 1 def step(self, state, action): """ 执行动作。 :param state: 当前状态。 :param action: 执行的动作。 :return: """ reward = self.r[state][action] next_state = action done = False if action == 5: done = True return next_state, reward, done def experience_replay(self): """ 记忆回放。 :return: """ # 随机选择一小批记忆样本。 batch = self.BATCH if self.memory_counter > self.BATCH else self.memory_counter minibatch = random.sample(self.replay_memory_store, batch) batch_state = None batch_action = None batch_reward = None batch_next_state = None batch_done = None for index in range(len(minibatch)): if batch_state is None: batch_state = minibatch[index][0] elif batch_state is not None: batch_state = np.vstack((batch_state, minibatch[index][0])) if batch_action is None: batch_action = minibatch[index][1] elif batch_action is not None: batch_action = np.vstack((batch_action, minibatch[index][1])) if batch_reward is None: batch_reward = minibatch[index][2] elif batch_reward is not None: batch_reward = np.vstack((batch_reward, minibatch[index][2])) if batch_next_state is None: batch_next_state = minibatch[index][3] elif batch_next_state is not None: batch_next_state = np.vstack((batch_next_state, minibatch[index][3])) if batch_done is None: batch_done = minibatch[index][4] elif batch_done is not None: batch_done = np.vstack((batch_done, minibatch[index][4])) # q_next:下一个状态的 Q 值。 q_next = self.session.run([self.q_eval], feed_dict={self.q_eval_input: batch_next_state}) q_target = [] for i in range(len(minibatch)): # 当前即时得分。 current_reward = batch_reward[i][0] # # 游戏是否结束。 # current_done = batch_done[i][0] # 更新 Q 值。 q_value = current_reward + self.gamma * np.max(q_next[0][i]) # 当得分小于 0 时,表示走了不可走的位置。 if current_reward < 0: q_target.append(current_reward) else: q_target.append(q_value) _, cost, reward = self.session.run([self.train_op, self.loss, self.reward_action], feed_dict={self.q_eval_input: batch_state, self.action_input: batch_action, self.q_target: q_target}) self.cost_his.append(cost) # if self.step_index % 1000 == 0: # print("loss:", cost) self.learn_step_counter += 1 def train(self): """ 训练。 :return: """ # 初始化当前状态。 current_state = np.random.randint(0, self.action_num - 1) self.epsilon = self.INITIAL_EPSILON while True: # 选择动作。 action = self.select_action(current_state) # 执行动作,得到:下一个状态,执行动作的得分,是否结束。 next_state, reward, done = self.step(current_state, action) # 保存记忆。 self.save_store(current_state, action, reward, next_state, done) # 先观察一段时间累积足够的记忆在进行训练。 if self.step_index > self.OBSERVE: self.experience_replay() if self.step_index > 10000: break if done: current_state = np.random.randint(0, self.action_num - 1) else: current_state = next_state self.step_index += 1 def pay(self): """ 运行并测试。 :return: """ self.train() # 显示 R 矩阵。 print(self.r) for index in range(5): start_room = index print("#############################", "Agent 在", start_room, "开始行动", "#############################") current_state = start_room step = 0 target_state = 5 while current_state != target_state: out_result = self.session.run(self.q_eval, feed_dict={ self.q_eval_input: self.state_list[current_state:current_state + 1]}) next_state = np.argmax(out_result[0]) print("Agent 由", current_state, "号房间移动到了", next_state, "号房间") current_state = next_state step += 1 print("Agent 在", start_room, "号房间开始移动了", step, "步到达了目标房间 5") print("#############################", "Agent 在", 5, "结束行动", "#############################") if __name__ == "__main__": q_network = DeepQNetwork() q_network.pay()这个DQN实现是一个简化的版本,简单介绍一下。在实际应用中,可能需要对网络结构、训练过程和超参数进行调整和优化。此外,代码中的 r 矩阵定义了状态转移和奖励,这是一个特定于问题的矩阵,需要根据具体问题进行设计
以上就算关于DQN的简单介绍.感谢你的阅读.
