因子分析（SPSS和Python）

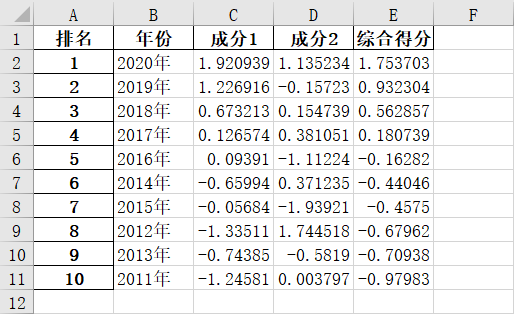
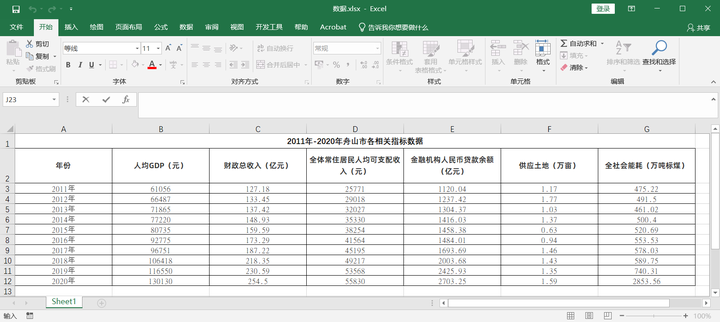
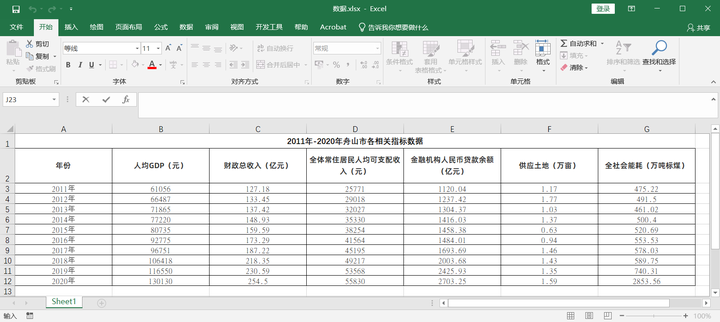
一、源数据

二、SPSS因子分析

2.1.导入数据

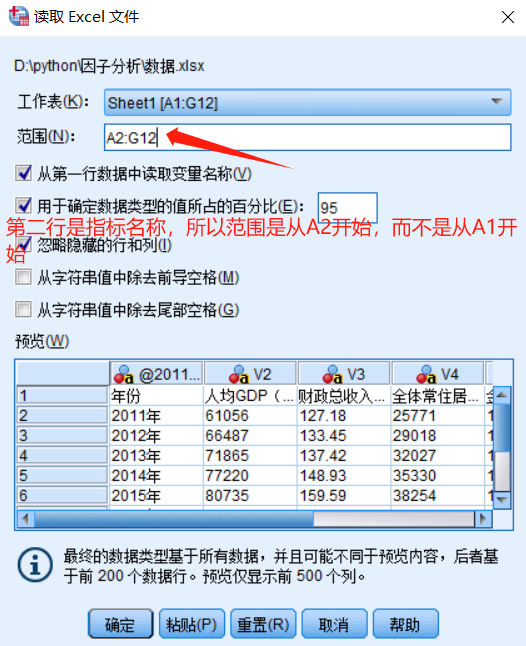
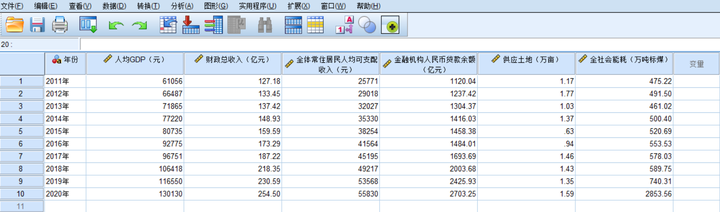
2.2.标准化处理

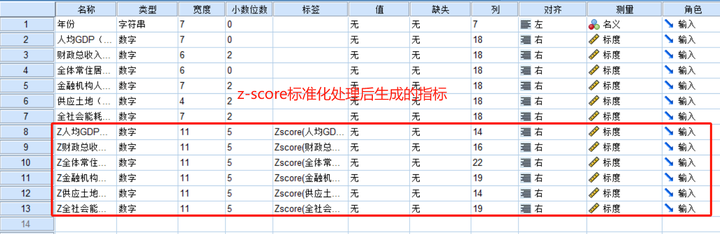
由于指标的量纲不同（单位不一致），因此，需要对数据进行标准化处理

2.3.因子分析

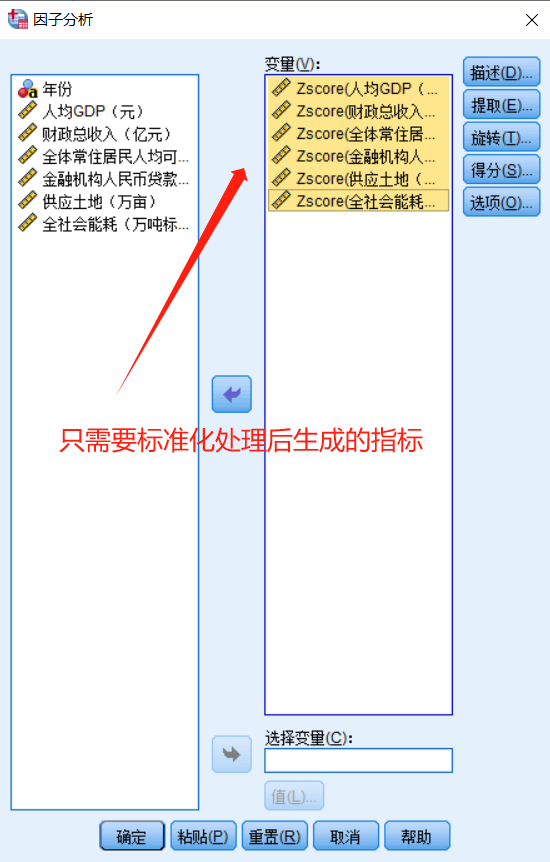
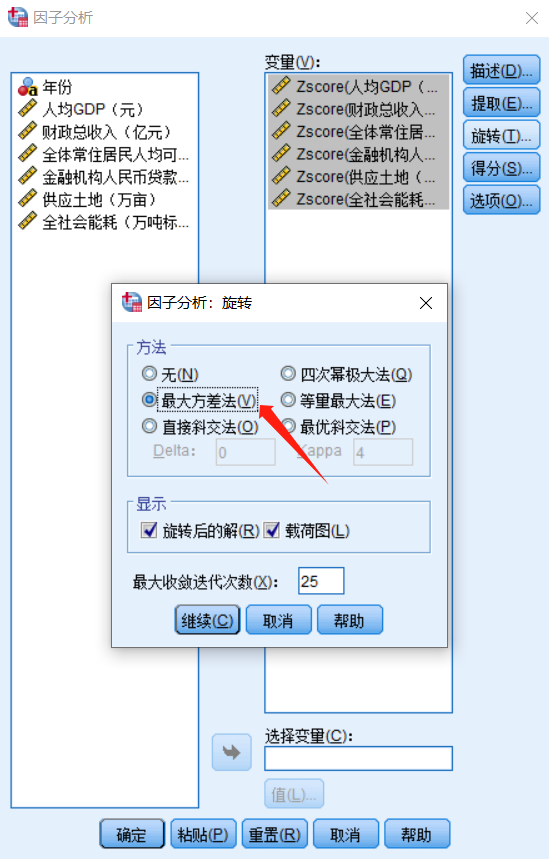
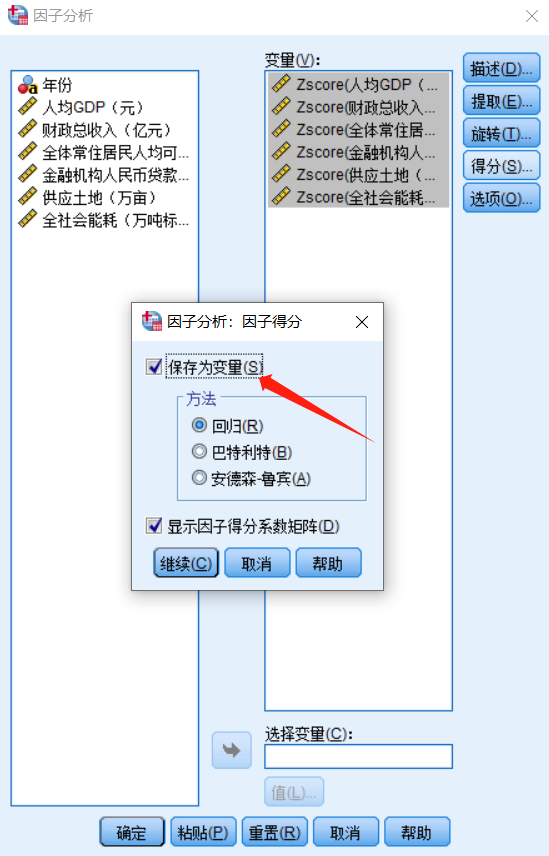
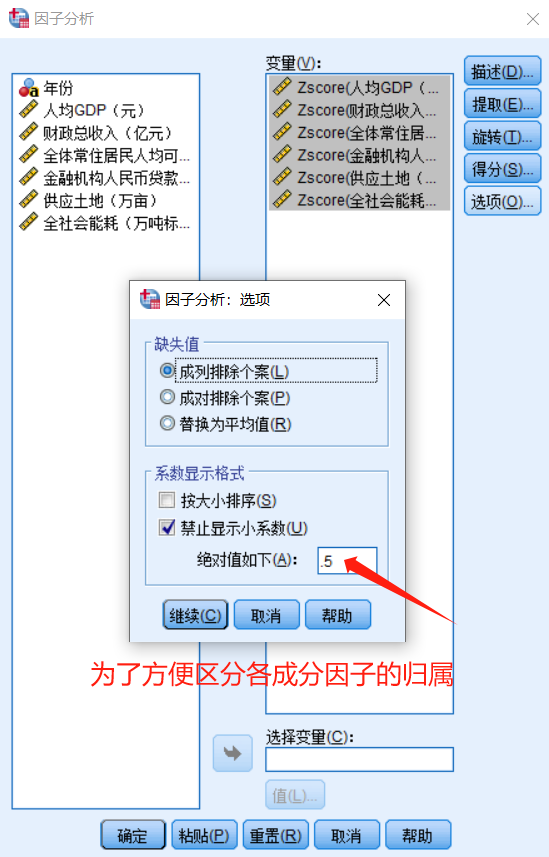
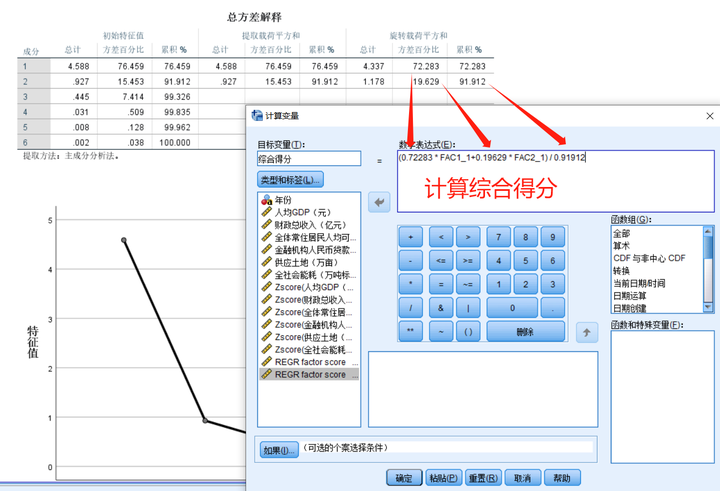
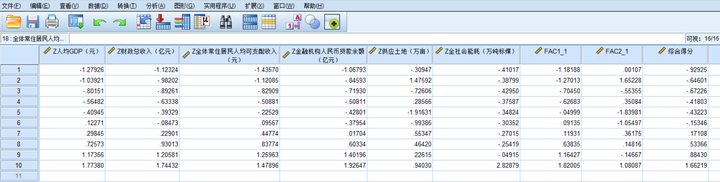
点击“确定”后，再回到“总方差解释”表格，以“旋转载荷平方和”中的各成分因子贡献率为权重，对因子得分做加权平均处理，可计算出综合得分

即：综合得分=(0.72283 * FAC1_1+0.19629 * FAC2_1) / 0.91912

其中，FAC1_1是成分1因子得分，FAC2_1是成分2因子得分，0.72283是成分1方差百分比（成分1因子贡献率），0.19629是成分2方差百分比（成分2因子贡献率），0.91912是累积方差百分比（累计因子贡献率）

2.4.输出结果

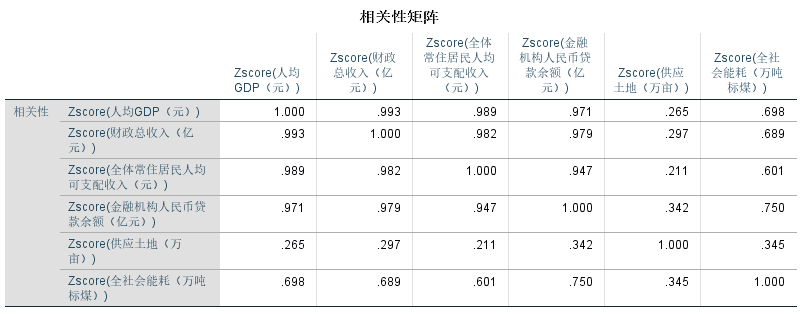
皮尔逊相关性矩阵：

通过计算指标之间的线性相关性，了解指标之间的相关性强弱，有助于确定因子个数和处理可能存在的共线性问题，如果相关性矩阵中大部分相关系数小于0.3且未通过充分性检验，则不适用于因子分析

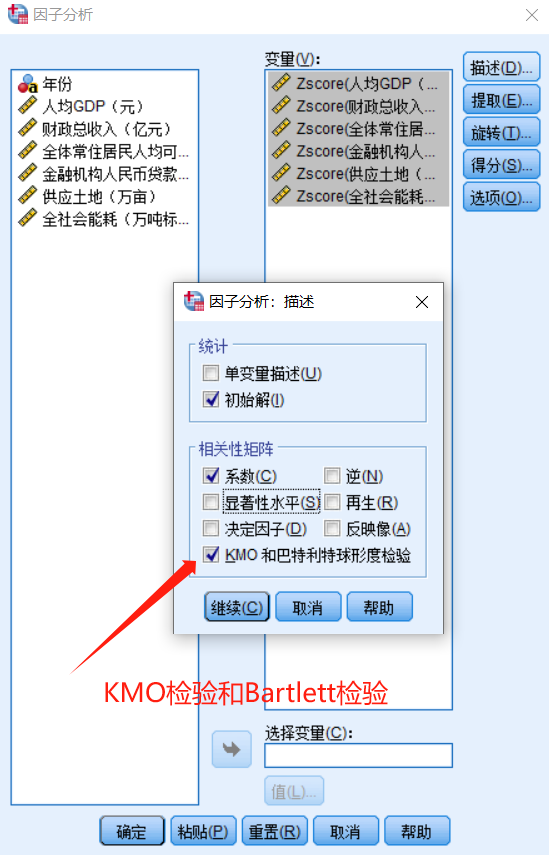
充分性检验（KMO和Bartlett检验）：

KMO检验：KMO值介于0和1之间，如果全部变量间相关系数平方和远大于偏相关系数平方和则KMO值接近1，KMO值越接近1越适合作因子分析。一般情况下，当KMO值大于0.6（严格一点就以0.7为阈值进行判断）时，表示指标之间的相关性较强，偏相关性较弱，适合做因子分析

Bartlett检验：原假设相关系数矩阵为单位阵，若得到的概率值小于规定的显著性水平（一般取0.05，严格一点就以0.01为阈值进行判断）则拒绝原假设，认为数据适合做因子分析，通俗来讲，即显著性水平越趋近于0则越适合做因子分析，反之则不能拒绝原假设，即数据不适合做因子分析

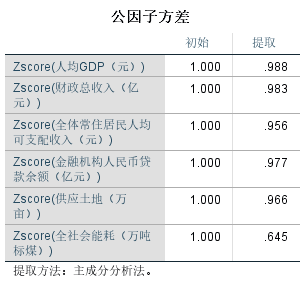
公因子方差：

从公因子方差可以看出各原始指标变量间的共同度，即各原始指标变量能被提取出的程度，由图可知，所有指标变量的共同度都在0.6以上，大部分指标变量的共同度在0.95以上，说明因子能解释指标变量中的大部分信息，适合进行因子分析

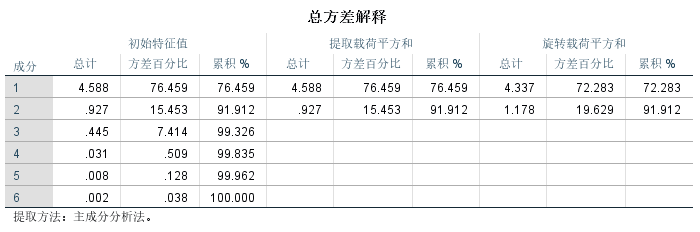
总方差解释：

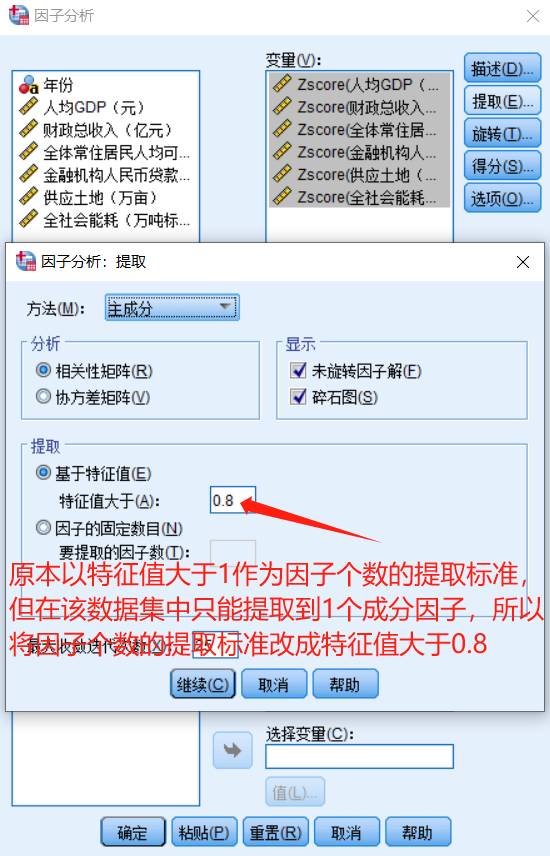
在总方差解释表中，可以看出提取2个成分因子时，其累计贡献率即可达到91.912%，说明选取2个成分因子就足以代替原来6个指标变量，能够解释原来6个指标变量所涵盖的大部分信息

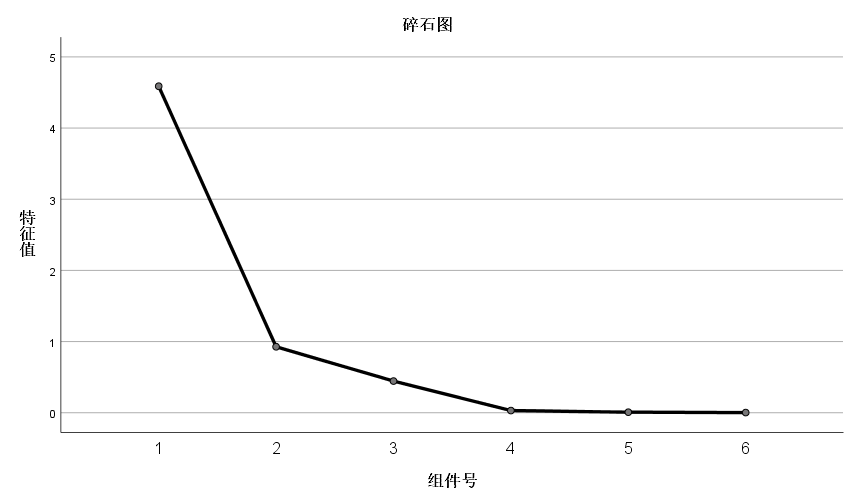
碎石图：

在碎石图中，可以看出第一个因子的特征值最高，方差贡献最大，第二个因子其次，第三个因子之后的特征值都较低了，对原来6个指标变量的解释程度也就较低，可以忽略，因此，提取2个成分因子是比较合适的

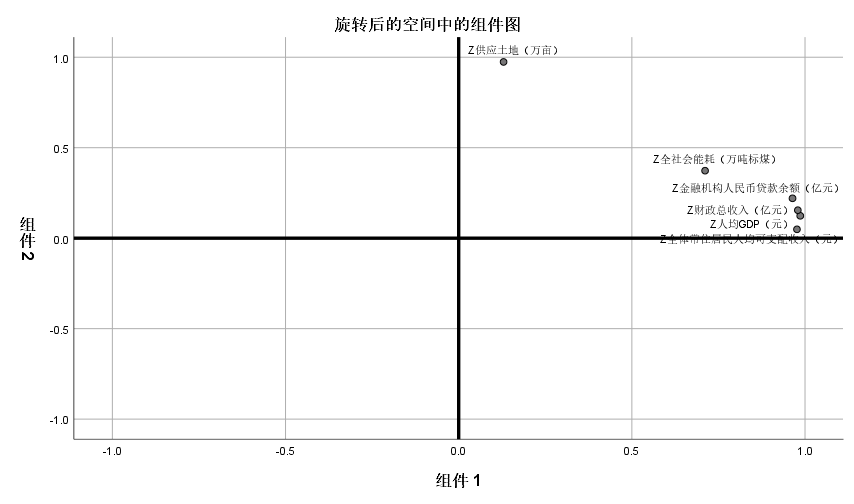
成分矩阵：

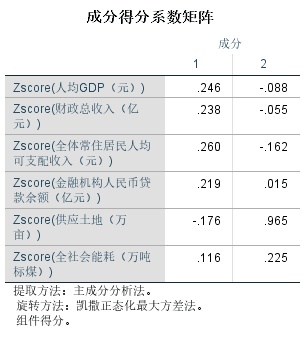
由成分矩阵可知，成分因子1主要解释人均GDP、财政总收入、全体常住居民人均可支配收入、金融机构人民币贷款余额、全社会能耗等5个指标变量的信息，可定义为综合发展因子F1，成分因子2主要解释供应土地这一个指标变量的信息，可定义为资源因子F2

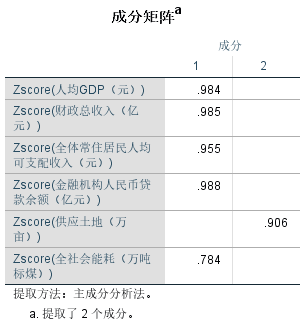
旋转后的成分矩阵：

在旋转之前，原始因子的载荷矩阵通常会产生一些问题，即一些变量与多个因子之间的载荷值都很高，而其他变量则没有明显的载荷值，在这种情况下，因子以及它们的载荷解释可能会变得模糊不清，难以解释或者解释力度不够，旋转后的成分矩阵则是能够更清晰地解释变量与因子之间的关系，从而提高了因子模型的可解释性

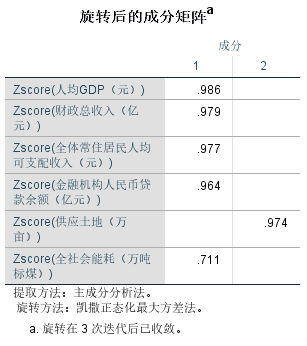
成分转换矩阵：

用来说明旋转前后成分因子间的系数对应关系

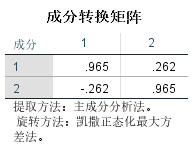
旋转后的空间中的组件图：

由图可知，人均GDP、财政总收入、全体常住居民人均可支配收入、金融机构人民币贷款余额、全社会能耗等5个指标变量基本是在同一个维度上的（横轴），这与综合发展因子F1是对应的，而供应土地这一个指标变量则是在另一个维度（纵轴），这则是与资源因子F2是对应的，说明提取2个因子是合理的，具有一定的可解释性

成分得分系数矩阵：

综合发展因子F1得分：

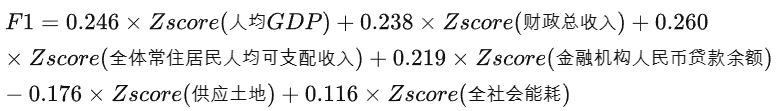
资源因子F2得分：

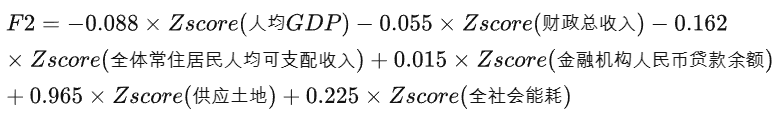
成分得分协方差矩阵：

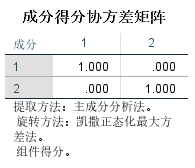
因子得分：

FAC1_1是成分1因子得分，即综合发展因子F1得分，FAC2_1是成分2因子得分，即资源因子F2得分，具体计算公式在“成分得分系数矩阵”已作说明

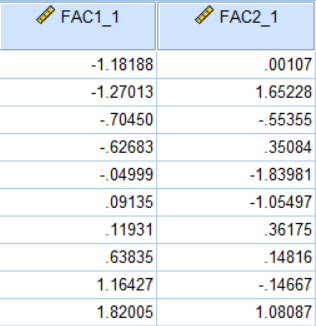
综合得分：

综合得分=(0.72283 * 综合发展因子F1得分+0.19629 * 资源因子F2得分) / 0.91912

三、Python因子分析

3.1.导入第三方库

# 导入第三方库 import pandas as pd import numpy as np from sklearn.preprocessing import StandardScaler from factor_analyzer import FactorAnalyzer,calculate_kmo,calculate_bartlett_sphericity import matplotlib.pyplot as plt import seaborn as sns  # 忽略警告 import warnings warnings.filterwarnings("ignore")  # 绘图时正常显示中文 plt.rcParams['font.sans-serif']=['SimHei'] plt.rcParams['axes.unicode_minus']=False

3.2.读取数据

# 读取数据 data=pd.read_excel('数据.xlsx',sheet_name='Sheet1',header=1) print(data)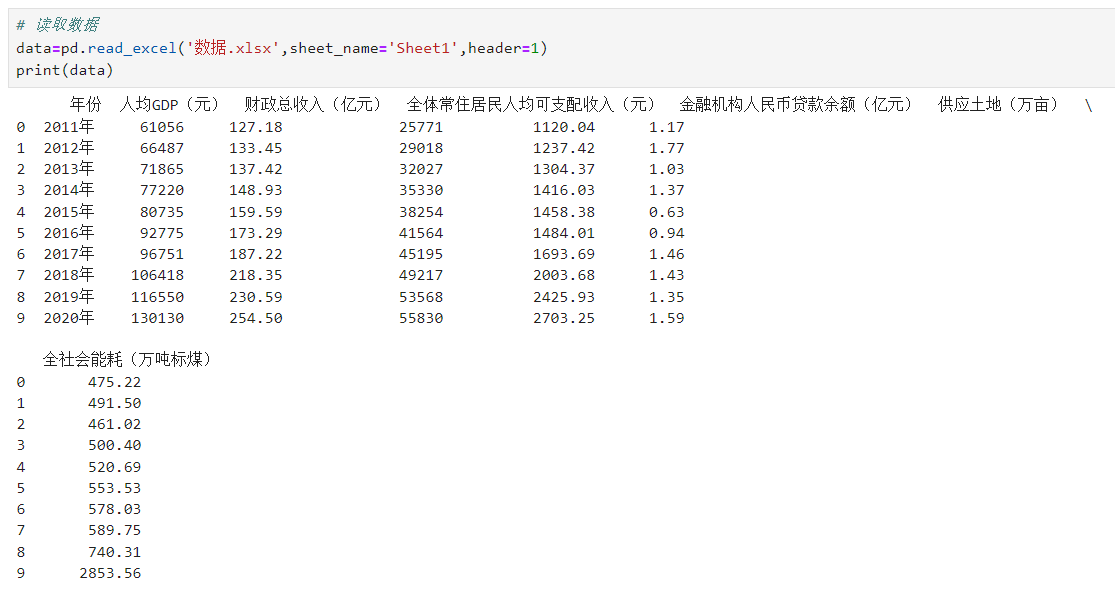

3.3.标准化处理

# 数据标准化处理 data_std=pd.DataFrame(StandardScaler().fit_transform(data.iloc[:,1:]),columns=data.columns[1:]) print(data_std)

3.4.皮尔逊相关性检验

# 皮尔逊相关性矩阵 data_corr=data_std.corr(method='pearson') print(data_corr)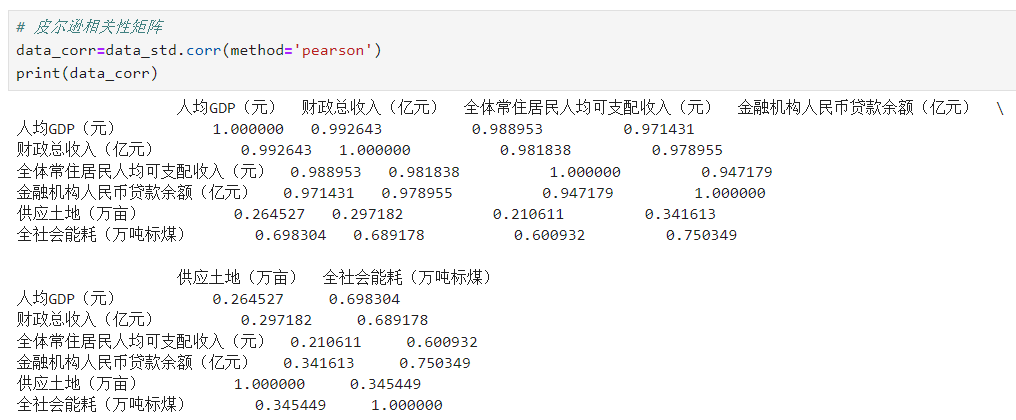

# 皮尔逊相关性热力图 plt.figure(figsize=(8,6)) sns.heatmap(data_corr,cmap='PuBu',annot=True,annot_kws={'fontsize':8}) plt.xticks(fontsize=8) plt.yticks(fontsize=8) plt.tight_layout()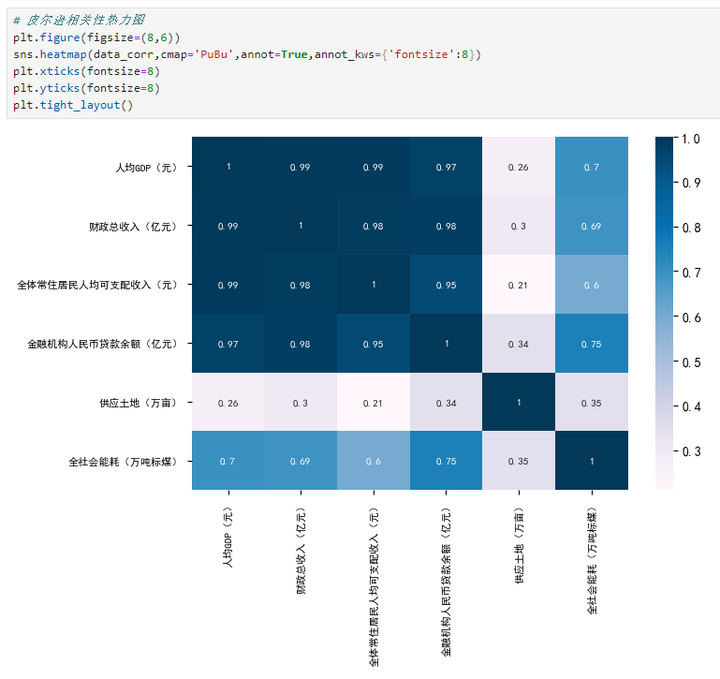

3.5.充分性检验（KMO检验和Bartlett检验）

# KMO检验和Bartlett检验 kmo=calculate_kmo(data_std) # KMO>0.6，则通过KMO检验 bartlett=calculate_bartlett_sphericity(data_std) # Bartlett<0.05，则通过Bartlett检验 print('\nKMO检验：',kmo[1],'\nBartlett检验：',bartlett[1],'\n')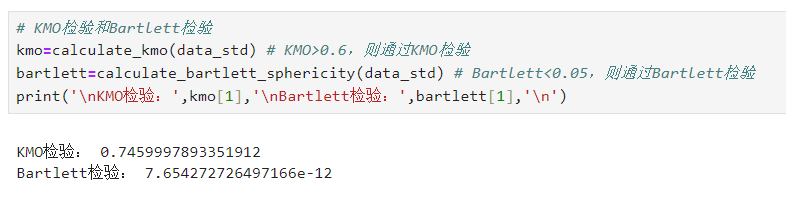

3.6.旋转前载荷矩阵

# 旋转前载荷矩阵 matrix=FactorAnalyzer(rotation=None,n_factors=8,method='principal') matrix.fit(data_std) f_contribution_var =matrix.get_factor_variance() matrices_var = pd.DataFrame() matrices_var["旋转前特征根"] = f_contribution_var[0] matrices_var["旋转前方差贡献率"] = f_contribution_var[1] matrices_var["旋转前方差累计贡献率"] = f_contribution_var[2] print('旋转前载荷矩阵的贡献率：\n',matrices_var,'\n')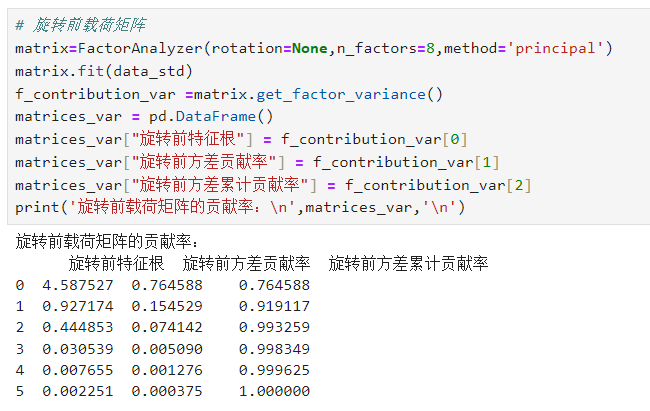

3.7.旋转后载荷矩阵

# 旋转后载荷矩阵 matrix_rotated=FactorAnalyzer(rotation='varimax',n_factors=2,method='principal') matrix_rotated.fit(data_std) f_contribution_var_rotated = matrix_rotated.get_factor_variance() matrices_var_rotated = pd.DataFrame() matrices_var_rotated["旋转后特征根"] = f_contribution_var_rotated[0] matrices_var_rotated["旋转后方差贡献率"] = f_contribution_var_rotated[1] matrices_var_rotated["旋转后方差累计贡献率"] = f_contribution_var_rotated[2] print('旋转后载荷矩阵的贡献率：\n',matrices_var_rotated,'\n')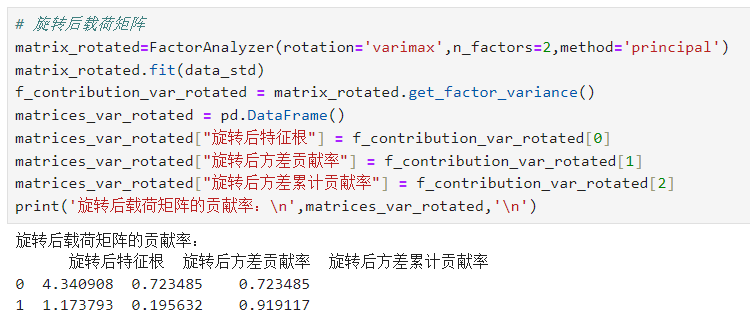

3.8.公因子方差表

# 公因子方差表 communalities=pd.DataFrame(matrix_rotated.get_communalities(),index=data_std.columns) print('公因子方差表：\n',communalities)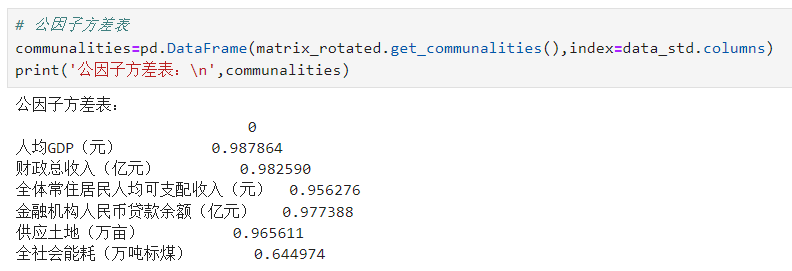

3.9.绘制碎石图

# 绘制碎石图 ev,v=matrix_rotated.get_eigenvalues() plt.figure(figsize=(6,6)) plt.scatter(range(1,data_std.shape[1]+1),ev) plt.plot(range(1,data_std.shape[1]+1),ev) plt.title('碎石图') plt.xlabel('因子个数') plt.ylabel('特征根')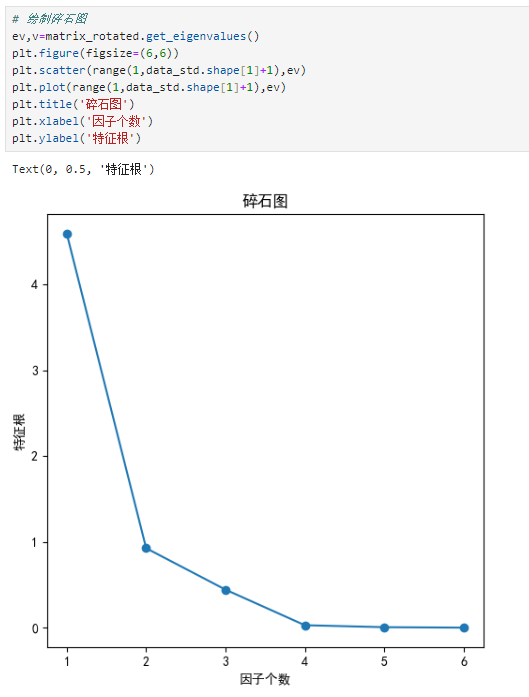

3.10.绘制成分矩阵热力图

# 绘制成分矩阵热力图 component_matrix=pd.DataFrame(np.abs(matrix_rotated.loadings_),index=data_std.columns,columns=['成分因子1','成分因子2']) plt.figure(figsize=(6,6)) sns.heatmap(component_matrix,annot=True,cmap='Blues') plt.tight_layout()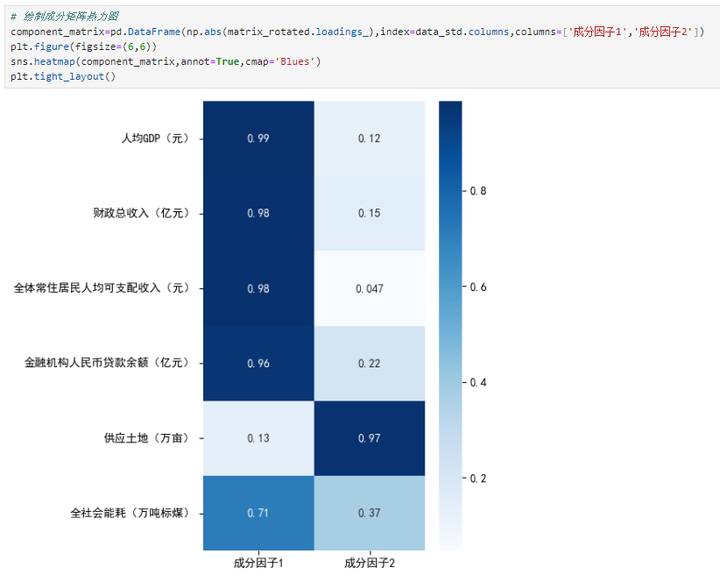

3.11.绘制成分矩阵二维空间组件图

# 绘制成分矩阵二维空间组件图 plt.figure(figsize=(6,6)) x=component_matrix.iloc[:,0] y=component_matrix.iloc[:,1] plt.scatter(x,y) for i in range(len(component_matrix)):     plt.annotate(component_matrix.index[i],(x[i],y[i]),textcoords='offset points',xytext=(-10,-10),ha='center',fontsize=8) plt.xlabel(component_matrix.columns[0]) plt.ylabel(component_matrix.columns[1]) plt.title('二维空间组件图') plt.grid(True)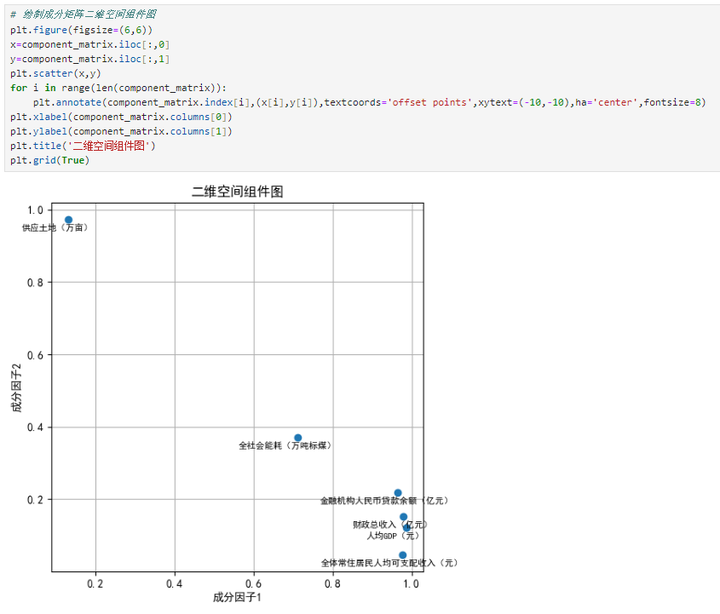

3.12.计算因子得分

# 计算因子得分 factor_score=pd.DataFrame(matrix_rotated.transform(data_std),columns=['成分1','成分2']) print(factor_score)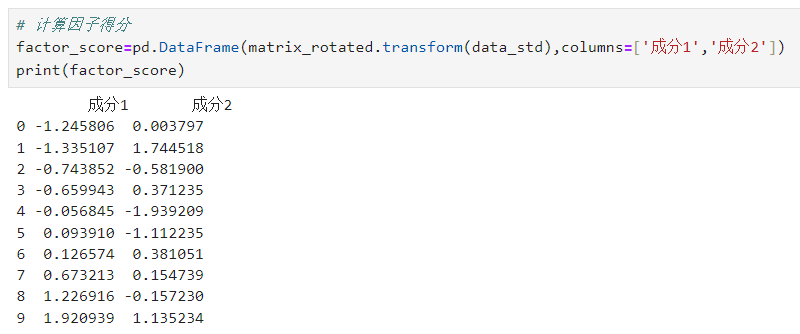

3.13.计算综合得分

# 计算综合得分 weight=matrices_var_rotated["旋转后方差贡献率"]/np.sum(matrices_var_rotated["旋转后方差贡献率"]) factor_score["综合得分"]=np.dot(factor_score,weight) factor_score=pd.concat([data.iloc[:,0],factor_score],axis=1) print('原顺序：\n',factor_score)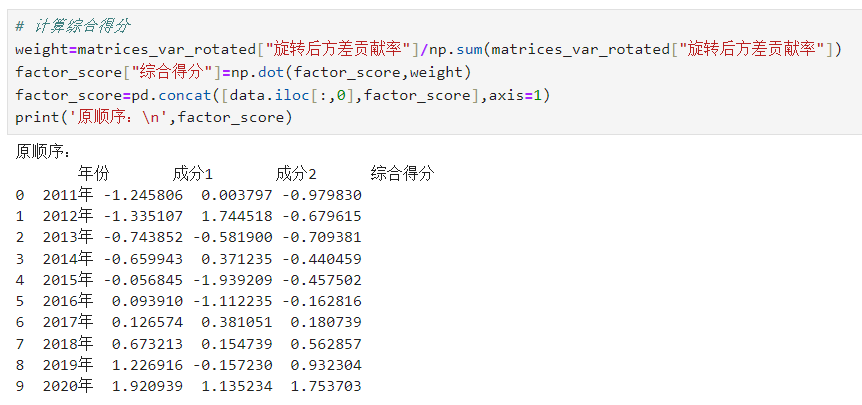

# 按综合得分从高到低排序 factor_score=factor_score.sort_values(by='综合得分',ascending=False) factor_score=factor_score.reset_index(drop=True) factor_score.index=factor_score.index+1 print('按综合得分从高到低排序：\n：',factor_score)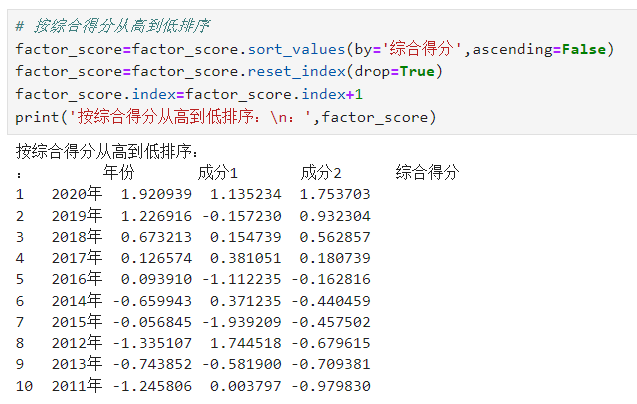

3.14.保存综合得分到excel

# 保存综合得分到新的excel factor_score.to_excel('综合得分.xlsx',index_label='排名')