1.引言
在文中,我们将深入探讨流行的激活函数,并分析它们在神经网络优化特性中的作用。激活函数在深度学习模型中扮演着至关重要的角色,因为它们为网络引入了非线性特性。尽管文献中描述了众多的激活函数,但它们并非一视同仁,各有优势。本文旨在阐明恰当选择激活函数的重要性,展示正确选择激活函数的方法,并讨论若不这样做可能引发的问题。
在我们深入讨论之前,首先导入标准库并构建基础功能。
# 导入os库,用于与操作系统交互,如文件路径操作 import os # 导入json库,用于处理JSON数据格式 import json # 导入math库,提供了数学函数的实现 import math # 导入numpy库,一个强大的数学库,支持大量的维度数组与矩阵运算 import numpy as np # 导入matplotlib.pyplot用于绘图 import matplotlib.pyplot as plt # 设置matplotlib为内联显示模式,主要用于Jupyter Notebook中 %matplotlib inline # 设置matplotlib的输出格式为svg和pdf,以便于高质量地导出图表 from IPython.display import set_matplotlib_formats set_matplotlib_formats('svg', 'pdf') # 导入seaborn库,一个基于matplotlib的高级绘图库,提供美观的统计图形 import seaborn as sns # 设置seaborn的默认样式 sns.set() # 从tqdm.notebook导入tqdm,用于在Jupyter Notebook中显示进度条 from tqdm.notebook import tqdm # 导入PyTorch库,一个流行的深度学习框架 import torch # 导入torch.nn模块,提供了构建神经网络所需的所有组件 import torch.nn as nn # 导入torch.nn.functional模块,提供了神经网络中常用的激活函数等 import torch.nn.functional as F # 导入torch.utils.data模块,提供了加载数据的工具,如Dataset和DataLoader import torch.utils.data as data # 导入torch.optim模块,提供了各种优化算法,如SGD、Adam等 import torch.optim as optim 在本文中,我们将创建一个函数,用于为我们在本教程中可能用到的所有库(这里是NumPy和PyTorch)设置随机种子。这样做的目的是确保我们的训练过程是可复现的。不过,需要指出的是,与在CPU上操作不同,即使设置了相同的随机种子,在不同的GPU架构上可能会得到不同的训练结果。本文中讨论的所有模型都是在NVIDIA GTX1080Ti GPU上进行训练的。
此外,接下来的代码单元定义了两个关键路径变量:DATASET_PATH和CHECKPOINT_PATH。DATASET_PATH是用于存储我们在教程中使用的下载数据集的目录。为了避免重复下载,建议将所有PyTorch数据集存储在一个统一的目录中。CHECKPOINT_PATH则是用于保存训练好的模型权重和其它相关文件的地方。所需的文件将会自动下载到指定位置。
# 定义数据集存放路径,下载的数据集(例如MNIST)将被保存在此文件夹 DATASET_PATH = "../data" # 定义预训练模型存放路径,训练好的模型将被保存在此文件夹 CHECKPOINT_PATH = "../saved_models/tutorial3" # 设置随机种子的函数,确保实验的可重复性 def set_seed(seed): # 为numpy设置随机种子 np.random.seed(seed) # 为PyTorch设置随机种子 torch.manual_seed(seed) # 如果GPU可用,则为GPU操作设置单独的种子 if torch.cuda.is_available(): torch.cuda.manual_seed(seed) torch.cuda.manual_seed_all(seed) # 调用函数设置随机种子为42 set_seed(42) # 由于GPU上一些操作为提高效率而采用随机实现, # 我们需要确保如果使用GPU,则所有操作都是确定性的,以保证结果的复现性 torch.backends.cudnn.deterministic = True torch.backends.cudnn.benchmark = False # 获取将在本教程中使用的设备,如果GPU可用则使用GPU,否则使用CPU device = torch.device("cpu") if not torch.cuda.is_available() else torch.device("cuda:0") # 打印出所使用的设备 print("Using device", device) 在本文中,我们将使用一系列预训练的模型。为了减小存储库的大小,特别是为了方便在ReadTheDocs上构建文档,这些模型文件被存储在了一个单独的仓库中。现在,下面的单元格将会尝试下载这些预训练模型。
import urllib.request # 导入urllib.request模块,用于请求网络资源 from urllib.error import HTTPError # 导入HTTPError,用于捕获HTTP请求过程中的错误 # 定义教程中预训练模型的存储Github URL基础路径 base_url = "https://raw.githubusercontent.com/phlippe/saved_models/main/tutorial3/" # 定义需要下载的预训练模型文件列表 pretrained_files = [ "FashionMNIST_elu.config", "FashionMNIST_elu.tar", "FashionMNIST_leakyrelu.config", "FashionMNIST_leakyrelu.tar", "FashionMNIST_relu.config", "FashionMNIST_relu.tar", "FashionMNIST_sigmoid.config", "FashionMNIST_sigmoid.tar", "FashionMNIST_swish.config", "FashionMNIST_swish.tar", "FashionMNIST_tanh.config", "FashionMNIST_tanh.tar" ] # 如果检查点路径不存在,则创建它 os.makedirs(CHECKPOINT_PATH, exist_ok=True) # 遍历每个文件名,检查文件是否已经存在;如果不存在,尝试下载 for file_name in pretrained_files: file_path = os.path.join(CHECKPOINT_PATH, file_name) # 完整的文件路径 if not os.path.isfile(file_path): # 如果文件不存在 file_url = base_url + file_name # 完整的文件URL print(f"Downloading {file_url}...") # 打印下载信息 try: urllib.request.urlretrieve(file_url, file_path) # 尝试下载文件 except HTTPError as e: # 如果下载过程中出现HTTP错误 print("下载过程中出现问题。请尝试从其他途径下载文件,或者联系作者,并附上完整的错误输出,包括以下错误信息:\n", e) 2.常见激活函数深度解析
在本文中,我们将探索几种常见的激活函数,并亲手实现它们。尽管这些函数大多可以在PyTorch的torch.nn模块中找到,但我们自己实现这些函数,可以更深入地理解其原理和应用。
为了便于后续比较不同激活函数的特性,我们首先定义一个基类ActivationFunction,后续的激活函数类都将继承自此基类。
class ActivationFunction(nn.Module): def __init__(self): super().__init__() self.name = self.__class__.__name__ self.config = {"name": self.name} 2.1.激活函数实现
我们将实现几个至今仍被广泛使用的“古老”激活函数:Sigmoid和Tanh。这两种激活函数在PyTorch中已有内置的函数和模块形式,但我们仍将手动实现它们,以加强理解。
class Sigmoid(ActivationFunction): def forward(self, x): return 1 / (1 + torch.exp(-x)) class Tanh(ActivationFunction): def forward(self, x): x_exp, neg_x_exp = torch.exp(x), torch.exp(-x) return (x_exp - neg_x_exp) / (x_exp + neg_x_exp) 2.2.ReLU及其变体
近年来,随着深度学习网络的发展,ReLU(修正线性单元)激活函数因其在大范围值内提供稳定梯度的强大优势而广受欢迎。我们将实现几种ReLU的变体:LeakyReLU、ELU和Swish。
- LeakyReLU在负值部分用较小的斜率替代了零,允许梯度在输入的这部分流动。
- ELU用指数衰减替换了负值部分。
- Swish是最近提出的激活函数,它平滑且非单调,有助于解决深层网络中的“死神经元”问题。
下面是这些激活函数的具体实现:
class ReLU(ActivationFunction): def forward(self, x): return x * (x > 0).float() class LeakyReLU(ActivationFunction): def __init__(self, alpha=0.1): super().__init__() self.config["alpha"] = alpha def forward(self, x): return torch.where(x > 0, x, self.config["alpha"] * x) class ELU(ActivationFunction): def forward(self, x): return torch.where(x > 0, x, torch.exp(x)-1) class Swish(ActivationFunction): def forward(self, x): return x * torch.sigmoid(x) 2.3.激活函数字典
为了方便以后使用,我们将实现的激活函数汇总到一个字典中,以名称映射到类对象。如果您实现了新的激活函数,也可以将其添加到此字典中,以便在未来的比较中使用。
act_fn_by_name = { "sigmoid": Sigmoid, "tanh": Tanh, "relu": ReLU, "leakyrelu": LeakyReLU, "elu": ELU, "swish": Swish } 以上就是对常见激活函数的深度解析和实现。通过这些示例,您可以更深入地理解每个激活函数的特性,并根据需要选择适合您模型的激活函数。
2.4.激活函数的可视化
为了直观了解每种激活函数的实质作用,我们将在下文中对它们进行可视化。除了实际的激活值外,函数的梯度也是一个重要方面,因为它对神经网络的优化至关重要。PyTorch允许我们通过简单地调用backward函数来计算梯度:
def get_grads(act_fn, x): """ 计算指定位置的激活函数的梯度。 输入: act_fn - 具有实现前向传播的"ActivationFunction"类的对象。 x - 1D输入张量。 输出: 一个与x大小相同的张量,包含在x处的act_fn的梯度。 """ x = x.clone().requires_grad_() # 将输入标记为需要存储梯度的张量 out = act_fn(x) out.sum().backward() # 求和导致梯度在x的每个元素中均匀流动 return x.grad # 通过"x.grad"访问x的梯度 现在我们可以可视化我们所有的激活函数,包括它们的梯度:
def vis_act_fn(act_fn, ax, x): # 运行激活函数 y = act_fn(x) y_grads = get_grads(act_fn, x) # 将x,y和梯度推回cpu以进行绘图 x, y, y_grads = x.cpu().numpy(), y.cpu().numpy(), y_grads.cpu().numpy() # 绘图 ax.plot(x, y, linewidth=2, label="ActFn") ax.plot(x, y_grads, linewidth=2, label="Gradient") ax.set_title(act_fn.name) ax.legend() ax.set_ylim(-1.5, x.max()) # 如果需要添加激活函数 act_fns = [act_fn() for act_fn in act_fn_by_name.values()] x = torch.linspace(-5, 5, 1000) # 我们想要可视化激活函数的范围 # 绘图 rows = math.ceil(len(act_fns)/2.0) fig, ax = plt.subplots(rows, 2, figsize=(8, rows*4)) for i, act_fn in enumerate(act_fns): vis_act_fn(act_fn, ax[divmod(i,2)], x) fig.subplots_adjust(hspace=0.3) plt.show() 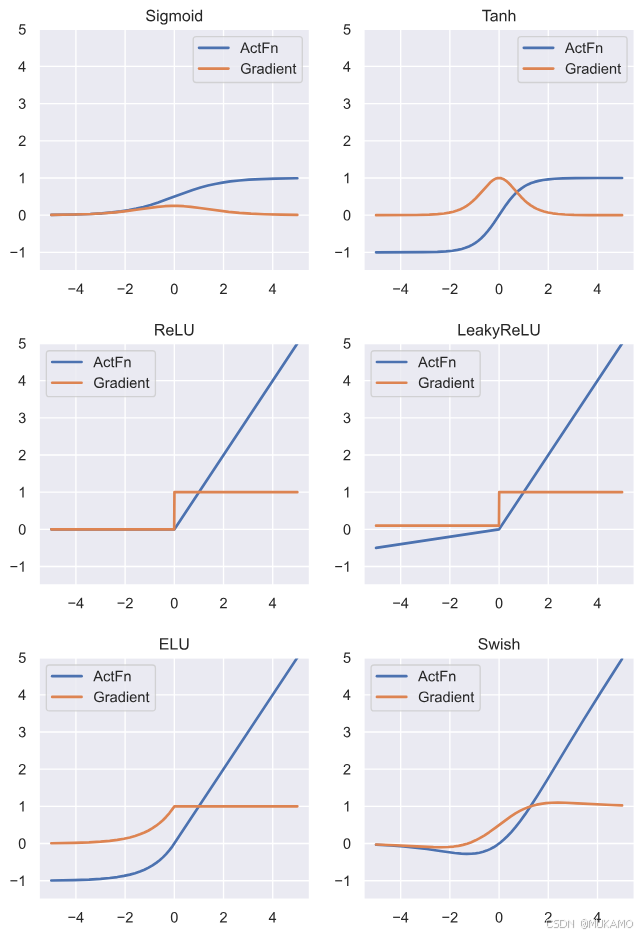
3.分析激活函数的效果
在实现和可视化激活函数之后,我们的目标是深入了解它们的效果。我们通过使用一个简单的神经网络,在FashionMNIST上进行训练,并检查模型的各个方面,包括性能和梯度流动。
3.1.配置
首先,让我们配置神经网络。所选网络将图像视为1D张量,并通过一系列线性层和指定的激活函数进行处理。请随时尝试其他网络架构。
class BaseNetwork(nn.Module): def __init__(self, act_fn, input_size=784, num_classes=10, hidden_sizes=[512, 256, 256, 128]): """ 输入: act_fn - 应在网络中用作非线性的激活函数对象。 input_size - 输入图像的像素大小 num_classes - 我们想要预测的类别数量 hidden_sizes - 指定神经网络中隐藏层大小的整数列表 """ super().__init__() # 根据指定的隐藏尺寸创建网络 layers = [] layer_sizes = [input_size] + hidden_sizes for layer_index in range(1, len(layer_sizes)): layers += [nn.Linear(layer_sizes[layer_index-1], layer_sizes[layer_index]), act_fn] layers += [nn.Linear(layer_sizes[-1], num_classes)] self.layers = nn.Sequential(*layers) # nn.Sequential将一系列模块总结为一个单独的模块,依次应用它们 # 我们将所有超参数存储在字典中,以保存和加载模型 self.config = {"act_fn": act_fn.config, "input_size": input_size, "num_classes": num_classes, "hidden_sizes": hidden_sizes} def forward(self, x): x = x.view(x.size(0), -1) # 将图像重塑为平向量 out = self.layers(x) return out 我们还添加了加载和保存模型的函数。超参数存储在配置文件中(简单的json文件):
def _get_config_file(model_path, model_name): # 存储超参数详细信息的文件名 return os.path.join(model_path, model_name + ".config") def _get_model_file(model_path, model_name): # 存储网络参数的文件名 return os.path.join(model_path, model_name + ".tar") def load_model(model_path, model_name, net=None): """ 从磁盘加载保存的模型。 输入: model_path - 检查点目录的路径 model_name - 模型的名称(str) net - (可选)如果提供,状态字典将加载到此模型中。否则,将创建一个新模型。 """ config_file, model_file = _get_config_file(model_path, model_name), _get_model_file(model_path, model_name) assert os.path.isfile(config_file), f"找不到配置文件\"{config_file}\"。确定这是正确的路径,并且您的模型配置存储在这里吗?" assert os.path.isfile(model_file), f"找不到模型文件\"{model_file}\"。确定这是正确的路径,并且您的模型存储在这里吗?" with open(config_file, "r") as f: config_dict = json.load(f) if net is None: act_fn_name = config_dict["act_fn"].pop("name").lower() act_fn = act_fn_by_name[act_fn_name](**config_dict.pop("act_fn")) net = BaseNetwork(act_fn=act_fn, **config_dict) net.load_state_dict(torch.load(model_file, map_location=device)) return net def save_model(model, model_path, model_name): """ 给定一个模型,我们保存state_dict和超参数。 输入: model - 要保存参数的网络对象 model_path - 检查点目录的路径 model_name - 模型的名称(str) """ config_dict = model.config os.makedirs(model_path, exist_ok=True) config_file, model_file = _get_config_file(model_path, model_name), _get_model_file(model_path, model_name) with open(config_file, "w") as f: json.dump(config_dict, f) torch.save(model.state_dict(), model_file) 我们还设置了要训练的数据集,即FashionMNIST。FashionMNIST是MNIST的一个更复杂的版本,包含衣服的黑白图像,而不是数字。10个类别包括裤子、外套、鞋子、包包等。为了加载这个数据集,我们将使用另一个PyTorch包,即torchvision(文档)。torchvision包包括流行的数据集、模型架构和计算机视觉的常见图像转换。我们将在本课程的许多笔记本中使用该包,以简化我们的数据集处理。
让我们在下面加载数据集,并可视化一些图像,以获得对数据的印象。
import torchvision from torchvision.datasets import FashionMNIST from torchvision import transforms # 应用于每个图像的转换 => 首先使它们成为张量,然后将其标准化到-1到1的范围内 transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))]) # 加载训练数据集。我们需要将其分为训练和验证部分 train_dataset = FashionMNIST(root=DATASET_PATH, train=True, transform=transform, download=True) train_set, val_set = torch.utils.data.random_split(train_dataset, [50000, 10000]) # 加载测试集 test_set = FashionMNIST(root=DATASET_PATH, train=False, transform=transform, download=True) # 我们定义一组数据加载器,我们以后可以用于各种目的。 # 注意,对于实际训练模型,我们将使用不同的数据加载器 # 具有较小的批量大小。 train_loader = data.DataLoader(train_set, batch_size=1024, shuffle=True, drop_last=False) val_loader = data.DataLoader(val_set, batch_size=1024, shuffle=False, drop_last=False) test_loader = data.DataLoader(test_set, batch_size=1024, shuffle=False, drop_last=False) exmp_imgs = [train_set[i][0] for i in range(16)] # 将图像组织成一个网格,以便更美观地可视化 img_grid = torchvision.utils.make_grid(torch.stack(exmp_imgs, dim=0), nrow=4, normalize=True, pad_value=0.5) img_grid = img_grid.permute(1, 2, 0) plt.figure(figsize=(8,8)) plt.title("FashionMNIST示例") plt.imshow(img_grid ) plt.axis('off') plt.show() plt.close() 
3.2.可视化初始化后的梯度流动
如前所述,激活函数的一个重要方面是它们如何通过网络传播梯度。设想我们有一个超过50层的非常深的神经网络。输入层即第一层的梯度,已经通过了超过50次激活函数,但我们仍希望它们保持合理的大小。如果激活函数的梯度(预期)明显小于1,我们的梯度将在到达输入层之前消失。如果激活函数的梯度大于1,梯度将指数增长并可能爆炸。
为了感受每个激活函数如何影响梯度,我们可以观察一个新初始化的网络,并为256张图像批量测量每个参数的梯度:
def visualize_gradients(net, color="C0"): """ 输入: net - BaseNetwork类的对象 color - 我们希望以何种颜色可视化直方图(便于激活函数的区分) """ net.eval() small_loader = data.DataLoader(train_set, batch_size=256, shuffle=False) imgs, labels = next(iter(small_loader)) imgs, labels = imgs.to(device), labels.to(device) # 将一批数据通过网络传递,并为权重计算梯度 net.zero_grad() preds = net(imgs) loss = F.cross_entropy(preds, labels) loss.backward() # 我们将可视化限制在权重参数上,并排除偏差以减少图表数量 grads = {name: params.grad.data.view(-1).cpu().clone().numpy() for name, params in net.named_parameters() if "weight" in name} net.zero_grad() # 绘图 columns = len(grads) fig, ax = plt.subplots(1, columns, figsize=(columns*3.5, 2.5)) fig_index = 0 for key in grads: key_ax = ax[fig_index%columns] sns.histplot(data=grads[key], bins=30, ax=key_ax, color=color, kde=True) key_ax.set_title(str(key)) key_ax.set_xlabel("梯度大小") fig_index += 1 fig.suptitle(f"激活函数{net.config['act_fn']['name']}的梯度大小分布", fontsize=14, y=1.05) fig.subplots_adjust(wspace=0.45) plt.show() plt.close() Seaborn在直方图包含小值时会打印警告。我们现在可以忽略它们。
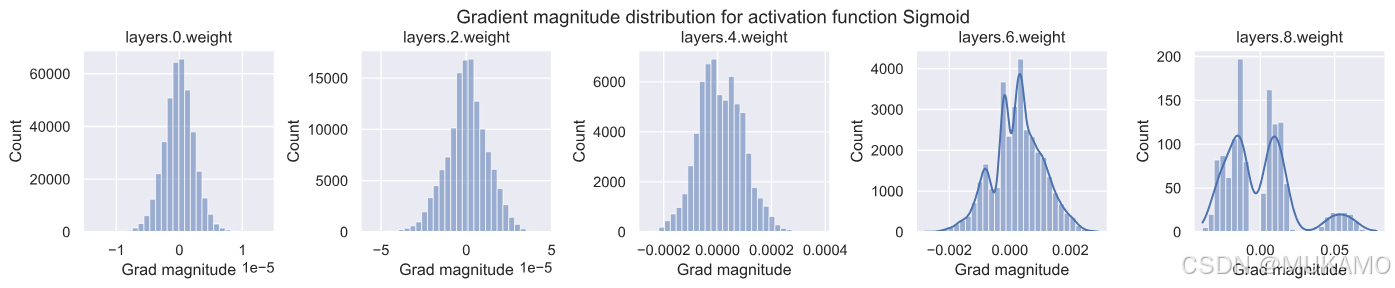
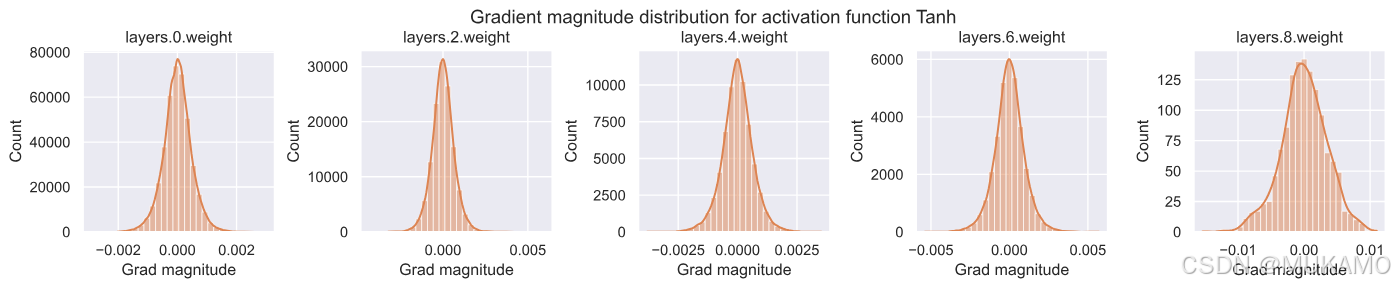
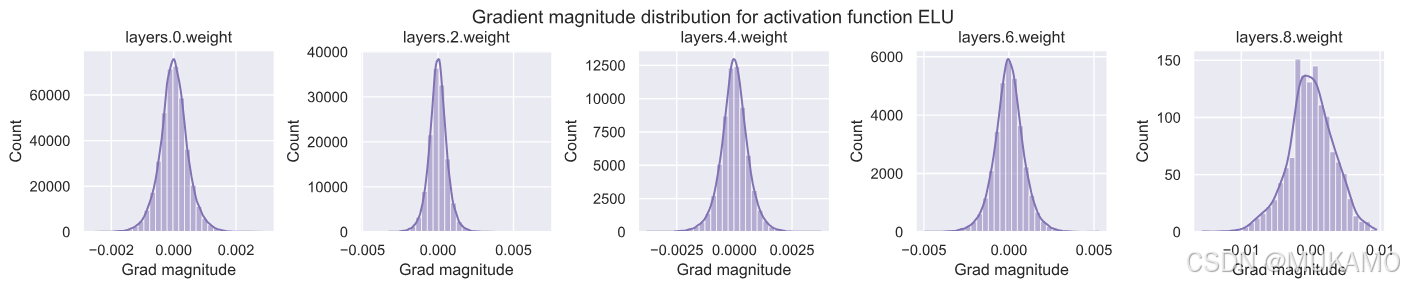
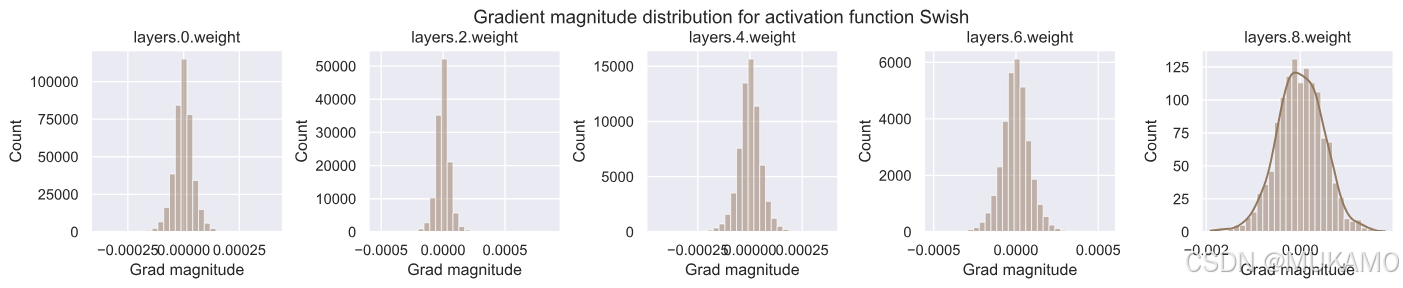
import warnings warnings.filterwarnings('ignore') # 为每种激活函数创建一个图表 for i, act_fn_name in enumerate(act_fn_by_name): set_seed(42) # 设置种子确保每种激活函数的权重初始化相同 act_fn = act_fn_by_name[act_fn_name]() net_actfn = BaseNetwork(act_fn=act_fn).to(device) visualize_gradients(net_actfn, color=f"C{i}") sigmoid激活函数表现出明显不良的行为。虽然输出层的梯度非常大,高达0.1,但输入层在所有激活函数中梯度范数最低,仅为1e-5。这是由于其最大梯度为1/4,在此设置中找不到适合所有层的学习率。
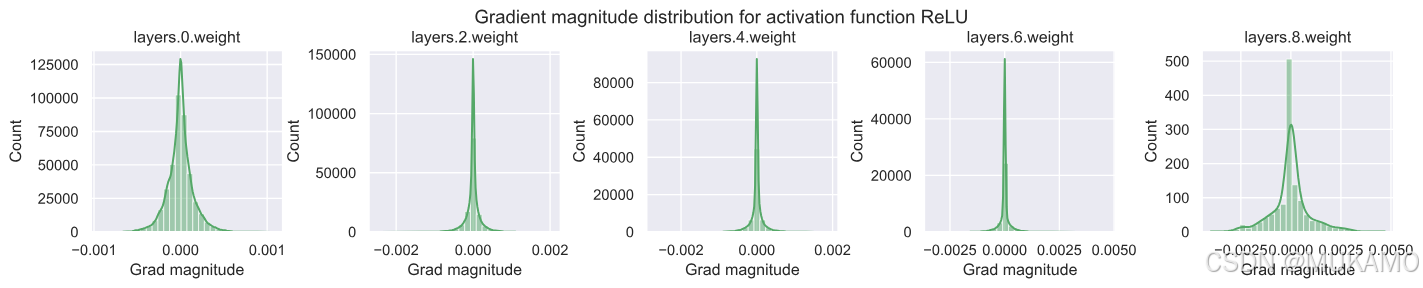
所有其他激活函数在所有层中显示出相似的梯度范数。有趣的是,ReLU激活函数在0附近有一个峰值,这是由其左侧的零部分和死神经元(我们将稍后仔细研究)造成的。
请注意,除了激活函数外,权重参数的初始化可能至关重要。默认情况下,PyTorch对线性层使用针对ReLU激活优化的Kaiming初始化。在第4个教程中,我们将更仔细地研究初始化,但目前假设Kaiming初始化对所有激活函数都相当有效。

3.3.模型训练
接下来,我们希望在FashionMNIST数据集上用不同的激活函数训练我们的模型,并比较所获得的性能。总的来说,我们的最终目标是在我们选择的数据集上实现最佳可能的性能。因此,我们在下一个单元格中编写了一个训练循环,包括每个epoch之后的验证,以及对最佳模型的最终测试:
def train_model(net, model_name, max_epochs=50, patience=7, batch_size=256, overwrite=False): """ 在FashionMNIST训练集上训练模型 输入: net - BaseNetwork类型的对象 model_name - (str) 模型名称,用于创建检查点名称 max_epochs - 我们想要(最大)训练的epoch数量 patience - 如果验证集上的性能在#patience个epoch内没有改善,我们将提前停止训练 batch_size - 训练中使用的批量大小 overwrite - 确定如何处理已经存在检查点的情况。如果为True,将被覆盖。否则,我们将跳过训练。 """ file_exists = os.path.isfile(_get_model_file(CHECKPOINT_PATH, model_name)) if file_exists and not overwrite: print("模型文件已存在。跳过训练...") else: if file_exists: print("模型文件存在,但将被覆盖...") # 定义优化器、损失和数据加载器 optimizer = optim.SGD(net.parameters(), lr=1e-2, momentum=0.9) # 默认参数,可自由更改 loss_module = nn.CrossEntropyLoss() train_loader_local = data.DataLoader(train_set, batch_size=batch_size, shuffle=True, drop_last=True, pin_memory=True) val_scores = [] best_val_epoch = -1 for epoch in range(max_epochs): ############# # 训练 # ############# net.train() true_preds, count = 0., 0 for imgs, labels in tqdm(train_loader_local, desc=f"Epoch {epoch+1}", leave=False): imgs, labels = imgs.to(device), labels.to(device) # 到GPU optimizer.zero_grad() # 在"loss.backward()"之前任何地方清零梯度 preds = net(imgs) loss = loss_module(preds, labels) loss.backward() optimizer.step() # 记录训练期间的统计数据 true_preds += (preds.argmax(dim=-1) == labels).sum() count += labels.shape[0] train_acc = true_preds / count ########## # 验证 # ########## val_acc = test_model(net, val_loader) val_scores.append(val_acc) print(f"[Epoch {epoch+1:2d}] 训练准确率: {train_acc*100.0:05.2f}%, 验证准确率: {val_acc*100.0:05.2f}%") if len(val_scores) == 1 or val_acc > val_scores[best_val_epoch]: print("\t (新的最佳性能,正在保存模型...)") save_model(net, CHECKPOINT_PATH, model_name) best_val_epoch = epoch elif best_val_epoch <= epoch - patience: print(f"由于最近{patience}个epochs没有改善,提前停止") break # 绘制验证准确率的曲线 plt.plot([i for i in range(1,len(val_scores)+1)], val_scores) plt.xlabel("Epochs") plt.ylabel("验证准确率") plt.title(f"{model_name}的验证性能") plt.show() plt.close() load_model(CHECKPOINT_PATH, model_name, net=net) test_acc = test_model(net, test_loader) print((f" 测试准确率: {test_acc*100.0:4.2f}% ").center(50, "=")+"\n") return test_acc 我们将为每种激活函数训练一个模型。如果您在CPU上运行这个笔记本,我们建议使用预训练模型以节省时间。
for act_fn_name in act_fn_by_name: print(f"正在训练使用{act_fn_name}激活的BaseNetwork...") set_seed(42) act_fn = act_fn_by_name[act_fn_name]() net_actfn = BaseNetwork(act_fn=act_fn).to(device) train_model(net_actfn, f"FashionMNIST_{act_fn_name}", overwrite=False) 毫不奇怪,使用sigmoid激活函数的模型显示出失败,并没有比随机性能更好(10个类别 => 随机概率为1/10)。
所有其他激活函数获得类似的性能。为了得出更准确的结论,我们必须使用多个种子训练模型并查看平均值。然而,“最佳”激活函数还取决于许多其他因素(隐藏大小、层数、层类型、任务、数据集、优化器、学习率等),因此在我们的案例中进行彻底的网格搜索是没有用的。在文献中,已经证明与深度网络一起工作的激活函数都是我们在这里实验的所有类型的ReLU函数,在特定网络中特定激活函数有小幅增益。
接下来,我们将训练我们的模型,使用不同的激活函数在FashionMNIST上,并比较所获得的性能。总之,我们的最终目标是在所选数据集上实现最佳可能的性能。因此,我们在下一个单元格中编写了一个训练循环,包括每个epoch之后的验证和对最佳模型的最终测试:
我们训练了一个针对每种激活函数的模型。如果您在CPU上运行这个笔记本,我们建议使用预训练模型以节省时间。
使用sigmoid激活函数的模型不出所料地失败了,并没有比随机性能更好(10个类别意味着随机概率为1/10)。
所有其他激活函数都获得了类似的性能。为了得出更准确的结论,我们需要使用多个不同的种子训练模型,并查看它们的平均性能。然而,“最佳”激活函数还取决于许多其他因素,如隐藏层大小、层数、层类型、任务、数据集、优化器、学习率等,因此在我们的情况下进行全面的网格搜索是没有用的。在文献中,已经表明与深度网络一起工作良好的激活函数都是我们在这里实验的ReLU函数类型,特定激活函数在特定网络中有小幅增益。
def test_model(net, data_loader): """ 在指定的数据集上测试模型。 输入: net - 已训练的BaseNetwork类型的模型 data_loader - 要测试的数据集的DataLoader对象(验证或测试) """ net.eval() true_preds, count = 0., 0 for imgs, labels in data_loader: imgs, labels = imgs.to(device), labels.to(device) with torch.no_grad(): preds = net(imgs).argmax(dim=-1) true_preds += (preds == labels).sum().item() count += labels.shape[0] test_acc = true_preds / count return test_acc 3.4.可视化激活分布
在模型训练完成后,我们可以观察模型内部实际的激活值。例如,ReLU中有多少神经元被设置为零?Tanh中的大部分值在哪里?为了回答这些问题,我们可以编写一个简单函数,该函数采用一个训练好的模型,将其应用于一批图像,并绘制网络内部激活的直方图:
def visualize_activations(net, color="C0"): activations = {} net.eval() small_loader = data.DataLoader(train_set, batch_size=1024) imgs, labels = next(iter(small_loader)) with torch.no_grad(): layer_index = 0 imgs = imgs.to(device) imgs = imgs.view(imgs.size(0), -1) # 我们需要手动遍历层以保存所有激活 for layer_index, layer in enumerate(net.layers[:-1]): imgs = layer(imgs) activations[layer_index] = imgs.view(-1).cpu().numpy() # 绘图 columns = 4 rows = math.ceil(len(activations)/columns) fig, ax = plt.subplots(rows, columns, figsize=(columns*2.7, rows*2.5)) fig_index = 0 for key in activations: key_ax = ax[fig_index//columns][fig_index%columns] sns.histplot(data=activations[key], bins=50, ax=key_ax, color=color, kde=True, stat="density") key_ax.set_title(f"Layer {key} - {net.layers[key].__class__.__name__}") fig_index += 1 fig.suptitle(f"Activation distribution for activation function {net.config['act_fn']['name']}", fontsize=14) fig.subplots_adjust(hspace=0.4, wspace=0.4) plt.show() plt.close() 为每种激活函数创建一个图表:
for i, act_fn_name in enumerate(act_fn_by_name): net_actfn = load_model(model_path=CHECKPOINT_PATH, model_name=f"FashionMNIST_{act_fn_name}").to(device) visualize_activations(net_actfn, color=f"C{i}") 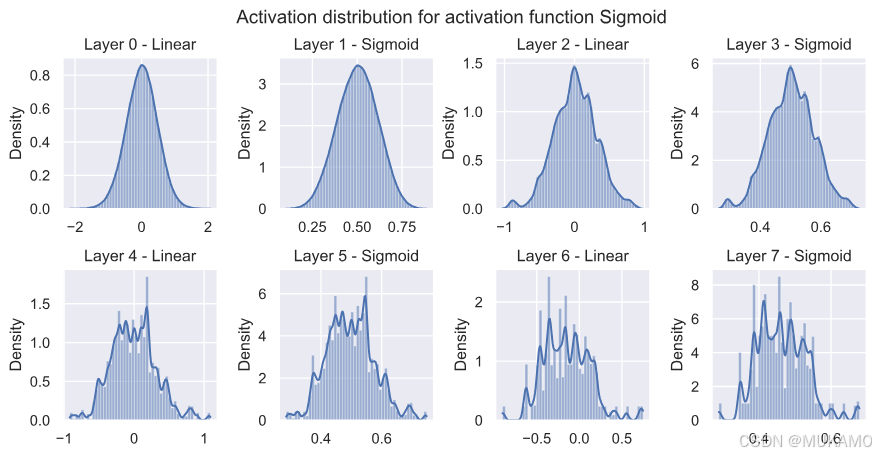
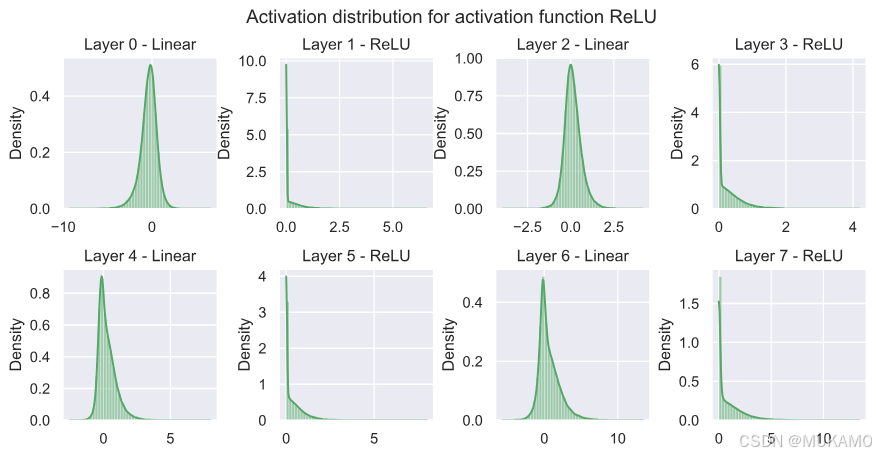
由于sigmoid激活的模型未能正确训练,激活值也不太有信息量,都集中在0.5(输入0时的激活)附近。
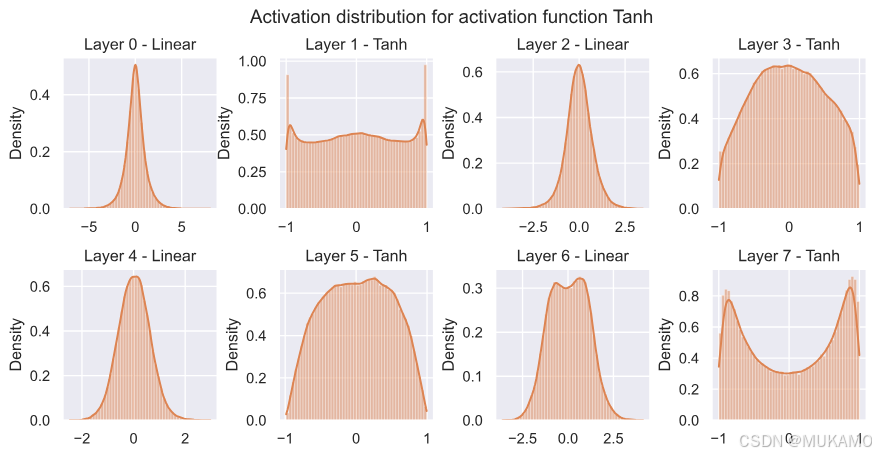
tanh显示出更多样化的行为。虽然输入层有更多神经元接近-1和1,梯度接近零,但连续两层的激活值更接近零。这可能是因为输入层在输入图像中寻找特定特征,而连续层将这些特征结合起来。最后一层的激活值再次更倾向于极端点,因为分类层可以看作是这些值的加权平均值(梯度将激活推向这些极端)。
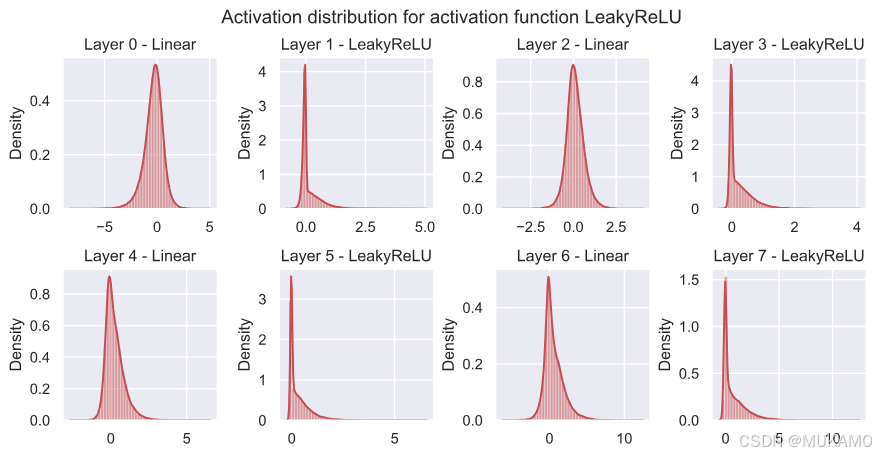
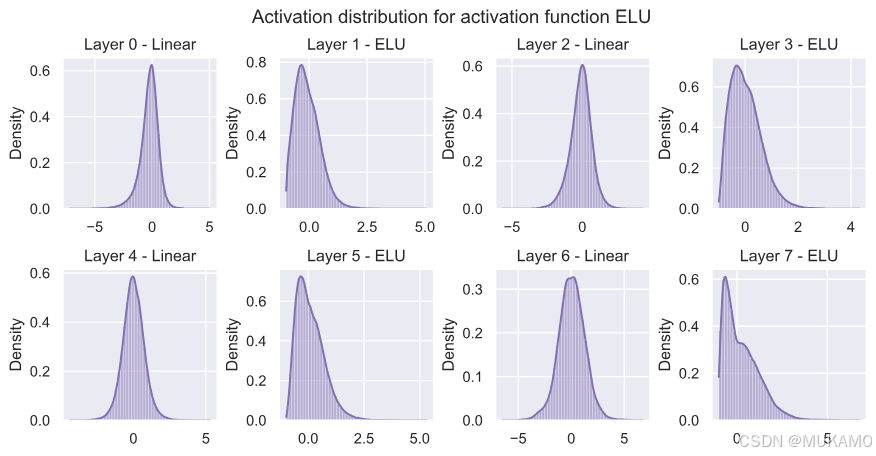
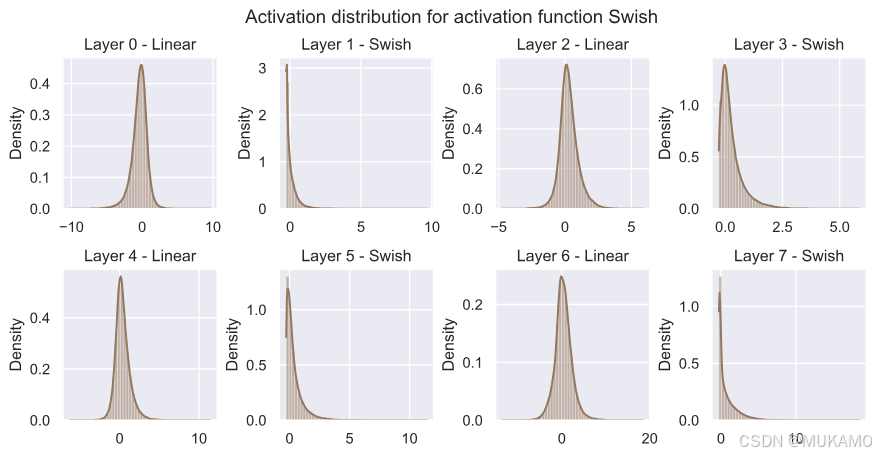
ReLU在0处有一个强烈的峰值,正如我们最初所预期的。由于负值没有梯度,网络在线性层之后的分布不是类似高斯的分布,而是对正值有更长的尾部。LeakyReLU表现出非常类似的行为,而ELU再次呈现出更类似高斯的分布。Swish激活似乎介于两者之间,尽管值得注意的是,Swish使用的值比其他激活函数显著更高(高达20)。
由于所有激活函数虽然表现出略有不同的行为,但在我们的简单网络中获得了类似的性能,显然“最佳”激活函数的选择实际上取决于许多因素,并且并不适用于所有可能的网络。
3.5.在ReLU网络中寻找死神经元
ReLU激活的一个已知缺点是“死神经元”的出现,即对任何训练输入都没有梯度的神经元。死神经元的问题在于,由于该层没有提供梯度,我们无法训练前一层的参数以获得除零以外的输出值。要使死神经元发生,ReLU前线性层的特定神经元的输出值必须对所有输入图像都是负的。考虑到神经网络中神经元的数量,这种情况的发生并不是不可能的。
为了更好地了解这是一个多么严重的问题,以及我们需要小心的时候,我们将测量不同网络中有多少死神经元。为此,我们实现了一个函数,该函数在整个训练集上运行网络,并记录是否有神经元对所有数据点都是0:
def measure_number_dead_neurons(net): # 对于每个神经元,我们最初设置一个布尔变量为1。如果它在任何时候的激活不等于0, # 我们将这个变量设置为0。在运行完整个训练集后,只有死神经元将保持为1。 neurons_dead = [ torch.ones(layer.weight.shape[0], device=device, dtype=torch.bool) for layer in net.layers[:-1] if isinstance(layer, nn.Linear) ] # 与BaseNetwork中的隐藏大小相同 net.eval() with torch.no_grad(): for imgs, labels in tqdm(train_loader, leave=False): # 运行整个训练集 layer_index = 0 imgs = imgs.to(device) imgs = imgs.view(imgs.size(0), -1) for layer in net.layers[:-1]: imgs = layer(imgs) if isinstance(layer, ActivationFunction): # 如果批量中的所有激活都是0,并且我们没有在最后几批中记录相反的情况? neurons_dead[layer_index] = torch.logical_and(neurons_dead[layer_index], (imgs == 0).all(dim=0)) layer_index += 1 number_neurons_dead = [t.sum().item() for t in neurons_dead] print("Number of dead neurons:", number_neurons_dead) print("In percentage:", ", ".join([f"{(100.0 * num_dead / tens.shape[0]):4.2f}%" for tens, num_dead in zip(neurons_dead, number_neurons_dead)])) 首先,我们可以为一个未训练的网络测量死神经元的数量:
set_seed(42) net_relu = BaseNetwork(act_fn=ReLU()).to(device) measure_number_dead_neurons(net_relu) 我们看到只有少数神经元是死的,但它们随着层的深度而增加。然而,由于前层权重的更新改变了后层的输入,我们拥有的少量死神经元并不是问题。因此,后层中的死神经元可能再次变为“活跃”。
对于训练过的网络(使用相同的初始化)情况如何?
net_relu = load_model(model_path=CHECKPOINT_PATH, model_name="FashionMNIST_relu").to(device) measure_number_dead_neurons(net_relu) 确实,在后层中死神经元的数量减少了。然而,应该注意的是,死神经元在输入层中尤为成问题。由于输入在epochs中不改变(训练集保持不变),训练网络无法使这些神经元重新活跃。尽管如此,输入数据通常具有足够高的标凊差,以降低死神经元的风险。
最后,我们检查死神经元数量如何随着层深度的增加而变化。例如,让我们看看以下10层神经网络:
set_seed(42) net_relu = BaseNetwork(act_fn=ReLU(), hidden_sizes=[256, 256, 256, 256, 256, 128, 128, 128, 128, 128]).to(device) measure_number_dead_neurons(net_relu) 死神经元的数量明显高于以前,这在第一次迭代中尤其损害了梯度流动。例如,倒数第二层中超过56%的神经元是死的,这造成了相当大的瓶颈。因此,对于非常深的网络,建议使用其他非线性激活,如Swish。
4.结论
在本文中,我们回顾了一系列六种激活函数(sigmoid、tanh、ReLU、LeakyReLU、ELU和Swish)在神经网络中的作用,并讨论了它们如何影响各层之间的梯度分布。Sigmoid倾向于在深层神经网络中失败,因为它所提供的最高梯度是0.25,导致早期层中的梯度消失。所有基于ReLU的激活函数都表现出良好的性能,并且除了原始的ReLU之外,它们没有死神经元的问题。在实现自己的神经网络时,建议从基于ReLU的网络开始,并根据网络的特性选择特定的激活函数。
参考文献
[1] Ramachandran, Prajit, Barret Zoph, 和 Quoc V. Le. “Searching for activation functions.” arXiv 预印本 arXiv:1710.05941 (2017). 论文链接
