阅读量:2
leetcode144、二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1: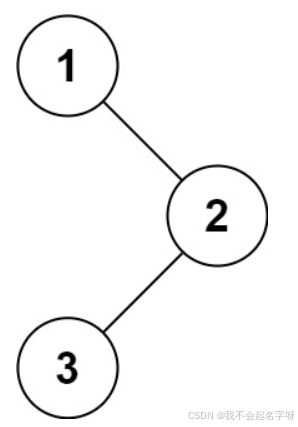
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4: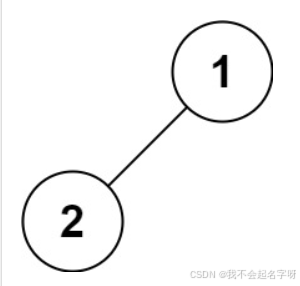
输入:root = [1,2]
输出:[1,2]
示例 5: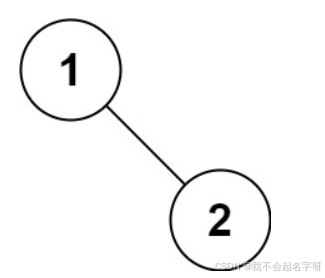
输入:root = [1,null,2]
输出:[1,2]
递归法
void preOrder(struct TreeNode* root,int* ret,int* returnSize){ if(root==NULL)return; ret[(*returnSize)++]=root->val; preOrder(root->left,ret,returnSize); preOrder(root->right,ret,returnSize); } int* preorderTraversal(struct TreeNode* root, int* returnSize) { int* ret=(int*)malloc(sizeof(int)*100); *returnSize=0; preOrder(root,ret,returnSize); return ret; } 迭代法
先将根节点加入数组,然后将根节点的右孩子入栈,再将左孩子入栈。出栈时左孩子先出栈,数组输出顺序为根左右。
int* preorderTraversal(struct TreeNode* root, int* returnSize) { struct TreeNode** stack=malloc(sizeof(struct TreeNode*)*1000); int stackSize=0; int *res=(int*)malloc(sizeof(int)*1000); int resSize=0; if(root==NULL){ *returnSize=0; return res; } stack[stackSize++]=root; while(stackSize>0){ struct TreeNode* node=stack[--stackSize]; res[resSize++]=node->val; if(node->right!=NULL) stack[stackSize++]=node->right; if(node->left!=NULL) stack[stackSize++]=node->left; } *returnSize=resSize; return res; } leetcode145、二叉树的后序遍历
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1: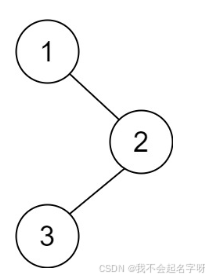
输入:root = [1,null,2,3]
输出:[3,2,1]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
递归法
void postorder(struct TreeNode* root,int* ret,int* returnSize){ if(root==NULL) return; postorder(root->left,ret,returnSize); postorder(root->right,ret,returnSize); ret[(*returnSize)++]=root->val; } int* postorderTraversal(struct TreeNode* root, int* returnSize) { int* ret=(int*)malloc(sizeof(int)*100); *returnSize=0; postorder(root,ret,returnSize); return ret; } 迭代法
前序遍历顺序调换:根右左->根左右
先将根节点加入数组,然后将根节点的左孩子入栈,再将右孩子入栈。出栈时右孩子先出栈,加入数组顺序为根右左。
将数组逆序输出:左右根
int* postorderTraversal(struct TreeNode* root, int* returnSize) { struct TreeNode** stack=malloc(sizeof(struct TreeNode*)*1000); int stackSize=0; int *res=(int*)malloc(sizeof(int)*1000); int resSize=0; if(root==NULL){ *returnSize=0; return res; } stack[stackSize++]=root; while(stackSize>0){ struct TreeNode* node=stack[--stackSize]; res[resSize++]=node->val; if(node->left!=NULL) stack[stackSize++]=node->left; if(node->right!=NULL) stack[stackSize++]=node->right; } //将数组逆序 for(int i=0,j=resSize-1;i<=j;i++,j--){ int tmp=res[i]; res[i]=res[j]; res[j]=tmp; } *returnSize=resSize; return res; } leetcode94、二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1: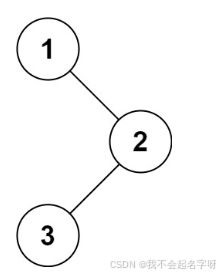
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
递归法
void inorder(struct TreeNode* root,int* ret,int* returnSize){ if(root==NULL) return; inorder(root->left,ret,returnSize); ret[(*returnSize)++]=root->val; inorder(root->right,ret,returnSize); } int* inorderTraversal(struct TreeNode* root, int* returnSize) { int* ret=(int*)malloc(sizeof(int)*100); *returnSize=0; inorder(root,ret,returnSize); return ret; } 迭代法
用一个指针来记录当前访问节点,先访问左子树,直到遍历到左子树的最左叶节点,输出该节点。输出该叶节点的父节点。然后访问该父节点的右子树,访问完右子树后输入该右节点。
int* inorderTraversal(struct TreeNode* root, int* returnSize) { struct TreeNode** stack = malloc(sizeof(struct TreeNode*) * 1024); // 假设栈的最大大小为 1024 int stackSize = 0; int* result = malloc(sizeof(int) * 1024); // 假设结果数组的最大大小为 1024 int resultSize = 0; struct TreeNode* cur = root;//借用指针的遍历来帮助访问节点 while(cur!=NULL||stackSize>0){ if(cur!=NULL){ stack[stackSize++]=cur; cur=cur->left; } else{ cur=stack[--stackSize]; result[resultSize++]=cur->val; cur=cur->right; } } *returnSize = resultSize; return result; } 