大家如果对几种最短路算法有一个基本的了解,大概会有一种模糊的感受,dijkstra是一个“加点”的过程,floyd是一个“选线”的过程。
Dijkstra
dijkstra很多教程都讲分成两个集合,但事实上写代码的时候并不需要,那为什么还要提这个呢,就是为了强化大家“从T集选点加入S集”这个观念。S集的特性是,里面所有的点都已经确定了它的最短距离了。待到所有的点都加入S集,那么问题就解决了
但是这个过程并不直观,为什么说现在优先队列里最短的那条边的另一个端点就是下一个要加入S的点呢?很多教程的例图都画的像PERT图一样,从左到右,边的设计也是非常不符合三角形两边之和大于第三边,我不是说不存在这样的情况,主要是会导致在纸上画不出来,长为10的边比长为3的边还短,很难直观,不适合人类去理解。我换种形式,大家就懂了
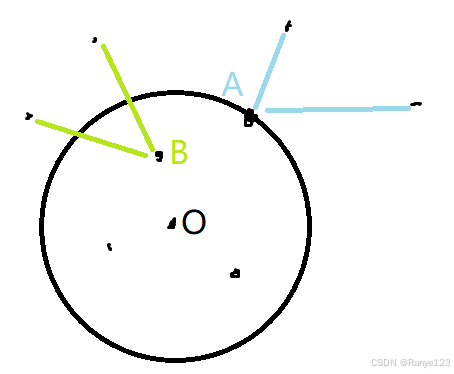
圈内的所有点的集合就是S集,刚入圈的新成员是A点。圈内所有点离O的距离都是<=OA的
假如我们现在想扩圈,找到一个新点加进来,那当然是既要考虑与A相连的点们(蓝线),又要考虑与圈内其他点相连的点们,比如和B相连的点(绿线)。而具体选哪一个,就要看这几个点谁离O最短了,对于A的朋友们X是OA+AX,对于B的朋友们是OB+BY。这也是为什么我们要将A相邻的所有边加入优先队列中。B的朋友们已经在了,就不用加了。
这个过程什么时候结束呢,就是当优先队列所有的线都被处理完了。这个圈子是被慢慢扩大的,只要圈外还有点,肯定是要继续向外伸线,不会漏掉哪个点;所有线处理完了,所有的点也处理完了,这个时候可以break这个while了
一些细节:
- G也是A相连的点,但是没必要考虑把G放进优先队列中,即OG<OA+AG时无需处理
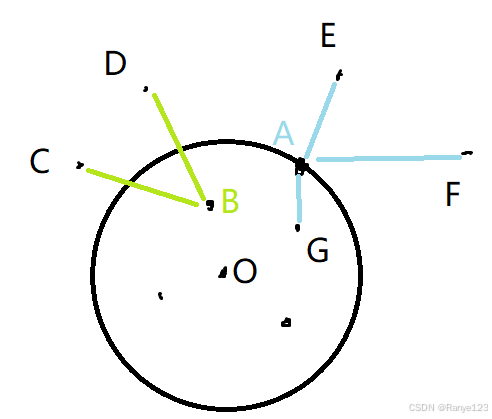
- 在处理各个边的过程中不免遇到点重复的情况,比如明明B已经进圈了,但是它和另一个点的连线还在优先队列中,在某时刻B又成了候选点,这时候再做以B为起点扩张的操作就没必要了。用一个vis数组存每个点是否进圈,如果vis[B]==true,及时continue
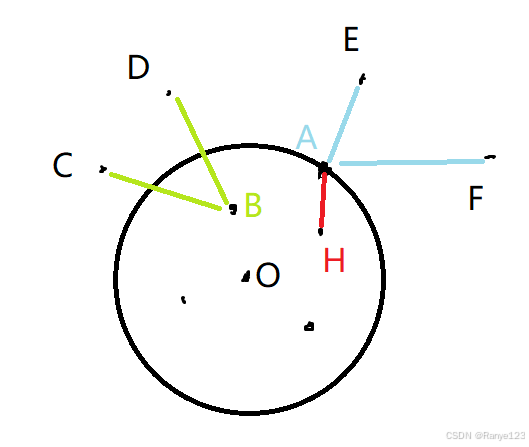
- dijkstra有一个很重要的特性是要求所有边都不能为负边。这是为什么呢?假如和A相连的有一个点H,AH<0,那么H自然是应当在圈内的,但是我们没找到A,就找不到H,所以H竟然在A之后进圈,我们的圈也就无法代表与O距离<=OA的点了,这样整条逻辑链就断掉了
Floyd
接下来讲讲Floyd,Floyd是一个好背但是不好理解的算法,但是如果没有理解,背起来ijk绝对会弄混
for(let k=0;k<n;k++) for(let i=0;i<n;i++) for(let j=0;j<n;j++) dis[i][j]=Math.min(dis[i][j], dis[i][k]+dis[k][j]); 首先要注意k在最外面。遍历时k为一个维度,ij为一个维度
它的含义是,每次引入k来判断是否能通过k这个点让ij距离最小
光这样就行了吗?是的!
假如说这个k,还没有找到i到k的最短路径,甚至于还没有找到i和k相连的路,dis[i][k]==INF,那这次比较不就失灵了吗?本来是要通过k进行线的变化的,但是这次却错过了,这样肯定不对吧
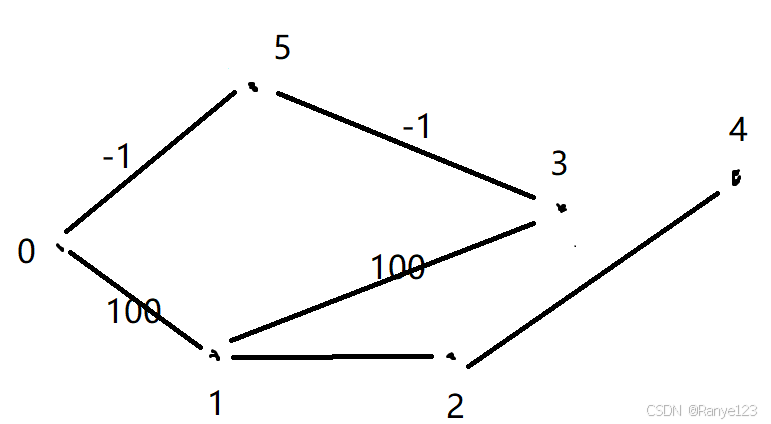
这个问题画一张图就清晰了,比如k=3,i=0,j=1。我们肉眼能看到,0到1是应该通过3比较近的(0-5-3-1),但由于0到3要经过5,k还没到5,dis[i][k]的值还是一个很大的值200,此时dis[i][j]保持原来的值100
但是这次错过不代表之后会错过,到了k=5的时候,dis[i][k](dis[0][5])已经是准的了,dis[k][j](dis[5][1])也是准的,这个时候是通过dis[0][5]+dis[5][1]更新的dis[0][1],而dis[5][1]就是dis[1][5],这个值同样是准的,所以“经过3”这个元素包含在dis[5][1]内了,虽然没有在k=3时发挥作用,但是会在k=5时发挥作用。这也是floyd能够一起算出任意两个点最短距离的妙处所在
就像我们当初学动态规划的时候,算最长公共子序列,看到两串字符串是acdefgabcdefg和abcdefg,也会想,万一我们光匹配前面的acdefg,匹配了这么长了,任何收场呢。但是最终来看,从全局的角度,是没有问题的
大家只要牢牢抓住一点,k从0到n的这个过程中,每一步,dis[i][j][k]都能切实的为i到k通过0~k的最小距离,且k++的时候,转移方程dis[i][j]=Math.min(dis[i][j], dis[i][k]+dis[k][j])也绝对不会出错,就可以了
