R语言实现对模型的参数优化与评价KS曲线、ROC曲线、深度学习模型训练、交叉验证、网格搜索

目录

一、模型性能评估

1、数据预测评估

2、概率预测评估

二、模型参数优化

1、训练集、验证集、测试集的引入

2、k折线交叉验证

2、网格搜索

---

一、模型性能评估

1、数据预测评估

### 数据预测评估 ###  # 加载包，不存在就进行在线下载后加载  if(!require(mlbench)) install.packages("mlbench")  library(mlbench)  data("BostonHousing")  # 数据分区  library(caret)  library(ggplot2)  library(lattice)  index <- createDataPartition(BostonHousing$medv,p = 0.75,list = FALSE)  train <- BostonHousing[index,]  test <- BostonHousing[-index,]  # 利用训练集构建模型,并对测试集进行预测  set.seed(1234)  fit <- lm(medv ~ .,data = train)  pred <- predict(fit,newdata = test)  # 自定义函数计算数值预测模型的评估指标  numericIndex <- function(obs,pred){    # 计算平均绝对误差MAE    MAE <- mean(abs(obs-pred))    # 计算均方误差MSE    MSE <- mean((obs-pred)^2)    # 计算均方根误差RMSE    RMSE <- sqrt(mean((obs-pred)^2))    # 计算归一化均方误差    NMSE <- sum((obs-pred)^2)/(sum((obs-mean(obs))^2))    # 计算判定系数Rsquared    Rsqured <- cor(pred,obs)^2    # 返回向量形式    return(c('MAE' = MAE,'MSE' = MSE,'RMSE' = RMSE,'NMSE' = NMSE,'Rsqured' = Rsqured))  }  # 计算各指标度量值  numericIndex(test$medv,pred)

# 利用caret包  library(caret)  postResample(pred,test$medv)

2、概率预测评估

### 混淆矩阵 ###  # install.packages("DAAG")  library(DAAG)  data(anesthetic)  anes1=glm(factor(nomove)~conc,family=binomial(link='logit'),data=anesthetic)  # 对模型做出预测结果  pre=predict(anes1,type='response') # 得到的是样本为1类别时的预测概率值  # 以0.5作为分界点  result <- ifelse(pre>0.5,1,0)  # 构建混淆矩阵  confusion<-table(actual=anesthetic$nomove,predict=result)  confusion  # 计算各指标（1为正样本，0为负样本）  (TP <- confusion[4])  (TN <- confusion[1])  (FP <- confusion[3])  (FN <- confusion[2])  (Accuracy <- (sum(TN) + sum(TP))/sum(confusion)) #准确率  (Accuracy <- (TN + TP)/sum(confusion)) #准确率  (Precision <- TP/(TP+FP)) # 精度  (Recall <- TP/(TP+FN)) # 灵敏性/召回率  (F1 <- 2*TP/(2*TP+FP+FN)) # F1-score  (FPR <- FP/(TN+FP)) #假正率

# 使用confusionMatrix函数  library(caret)  confusionMatrix(data = factor(result), # 预测结果                  reference = factor(anesthetic$nomove), # 实际结果                  positive = '1', # 指定类别1为正样本                  mode = "prec_recall") # 设置为精度和查全率模式

### ROC曲线  ###  # 构建结果数据集  result <- data.frame(pre_prob = pre,true_label = anesthetic$nomove)  result <- result[order(result$pre_prob,decreasing = T),] # 按照预测概率值进行降序排序  result$cumsum <-  cumsum(rep(1,nrow(result))) # 统计累计样本数量  result$poscumsum <- cumsum(result$true_label) # 统计累计正样本数量  result$tpr <- round(result$poscumsum/sum(result$true_label==1),3) # 计算真正率  result$fpr <- round((result$cumsum-result$poscumsum)/sum(result$true_label==0),3) # 计算假正率  result$lift <- round((result$poscumsum/result$cumsum)/(sum(result$true_label==1)/nrow(result)),2) # 计算提升度  head(result)  tail(result)  # 画出roc曲线  library(ggplot2)  if(!require(ROCR)) install.packages("ROCR")  library(ROCR)  ggplot(result) +    geom_line(aes(x = result$fpr, y = result$tpr),color = "red1",size = 1.2) +    geom_segment(aes(x = 0, y = 0, xend = 1, yend = 1), color = "grey", lty = 2,size = 1.2) +    annotate("text", x = 0.5, y = 1.05,             label=paste('AUC:',round(ROCR::performance(prediction(result$pre_prob, result$true_label),'auc')@y.values[[1]],3)),             size=6, alpha=0.8) +    scale_x_continuous(breaks=seq(0,1,.2))+    scale_y_continuous(breaks=seq(0,1,.2))+    xlab("False Postive Rate")+    ylab("True Postive Rate")+    ggtitle(label="ROC - Chart")+    theme_bw()+    theme(      plot.title=element_text(colour="gray24",size=12,face="bold"),      plot.background = element_rect(fill = "gray90"),      axis.title=element_text(size=10),      axis.text=element_text(colour="gray35"))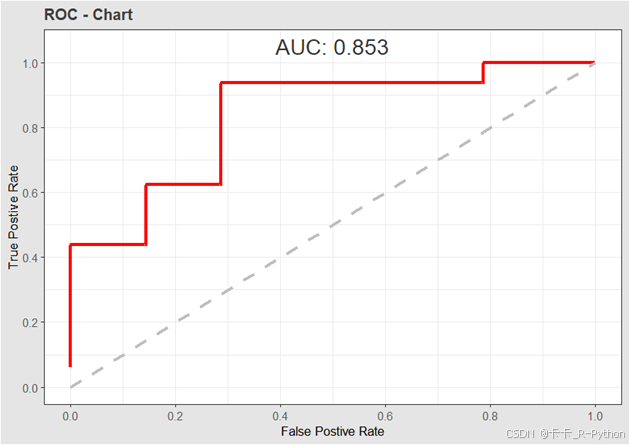

# 利用ROCR包绘制roc曲线  library(ROCR)  pred1 <- prediction(pre,anesthetic$nomove)  # 设置参数，横轴为假正率fpr，纵轴为真正率tpr  perf <- performance(pred1,'tpr','fpr')  # 绘制ROC曲线  plot(perf,main = "利用ROCR包绘制ROC曲线")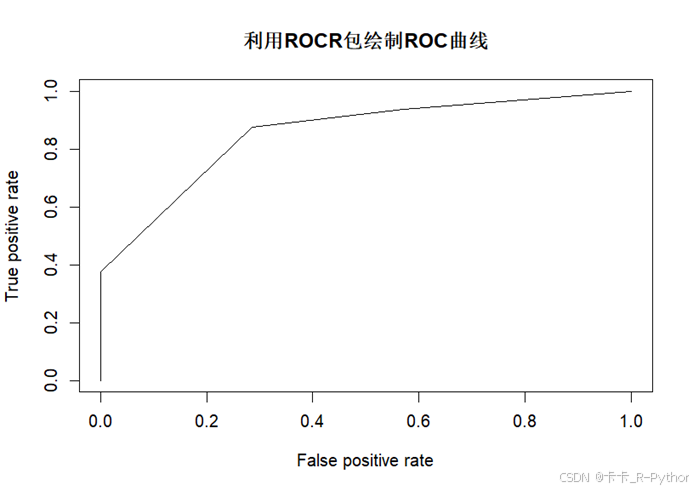

# 计算AUC值  auc.adj <- performance(pred1,'auc')  auc <- auc.adj@y.values[[1]]  auc  # 画出KS曲线  ggplot(result) +    geom_line(aes((1:nrow(result))/nrow(result),result$tpr),colour = "red2",size = 1.2) +    geom_line(aes((1:nrow(result))/nrow(result),result$fpr),colour = "blue3",size = 1.2) +    annotate("text", x = 0.5, y = 1.05, label=paste("KS=", round(which.max(result$tpr-result$fpr)/nrow(result), 4),                                                    "at Pop=", round(max(result$tpr-result$fpr), 4)), size=6, alpha=0.8)+    scale_x_continuous(breaks=seq(0,1,.2))+    scale_y_continuous(breaks=seq(0,1,.2))+    xlab("Total Population Rate")+    ylab("TP/FP Rate")+    ggtitle(label="KS - Chart")+    theme_bw()+    theme(      plot.title=element_text(colour="gray24",size=12,face="bold"),      plot.background = element_rect(fill = "gray90"),      axis.title=element_text(size=10),      axis.text=element_text(colour="gray35"))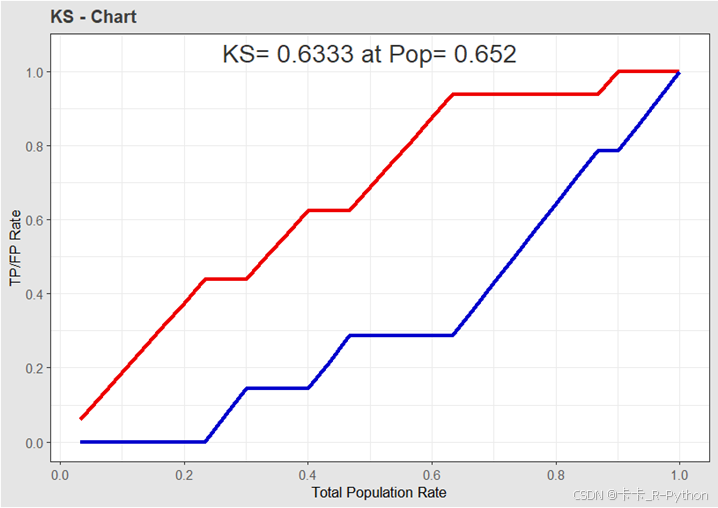

# 画累积提升图  ggplot(result) +    geom_line(aes(x = (1:nrow(result))/nrow(result), y = result$lift),color = "red3",size = 1.2) +    scale_x_continuous(breaks=seq(0,1,.2))+    xlab("Total Population Rate")+    ylab("Lift value")+    ggtitle(label="LIFT - Chart")+    theme_bw()+    theme(      plot.title=element_text(colour="gray24",size=12,face="bold"),      plot.background = element_rect(fill = "gray90"),      axis.title=element_text(size=10),      axis.text=element_text(colour="gray35"))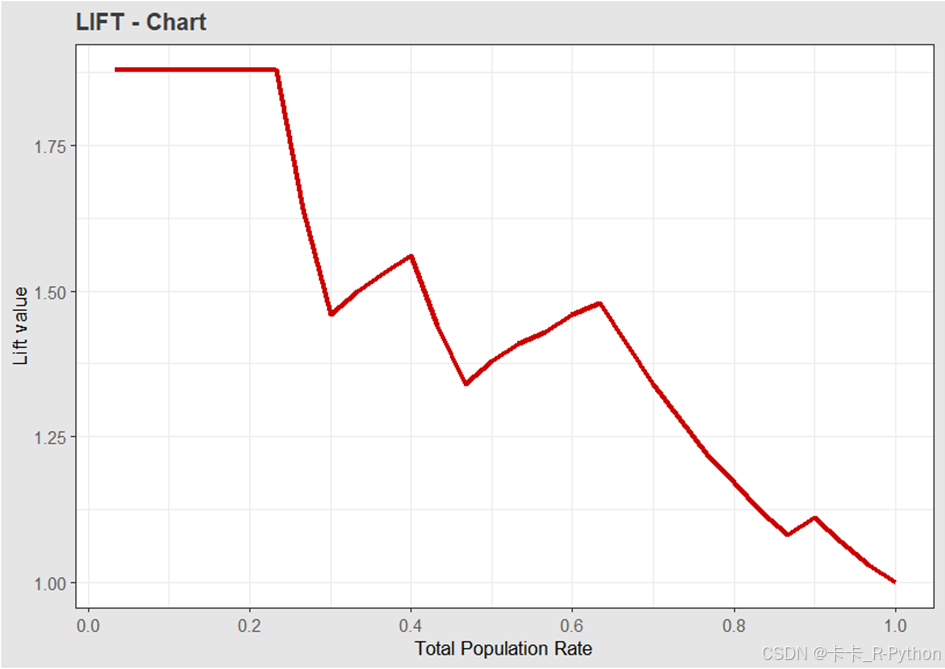

# 读入封装好的R代码  source('自定义绘制各种曲线函数.R')  # 加载ROCR.simple数据集  library(ROCR)  data(ROCR.simple)  # 绘制各种曲线  pc <- plotCurve(pre_prob=ROCR.simple$predictions,                  true_label=ROCR.simple$labels)  # 查看各种曲线  library(gridExtra)  grid.arrange(pc$roc_curve,pc$ks_curve,pc$lift_curve,ncol = 3)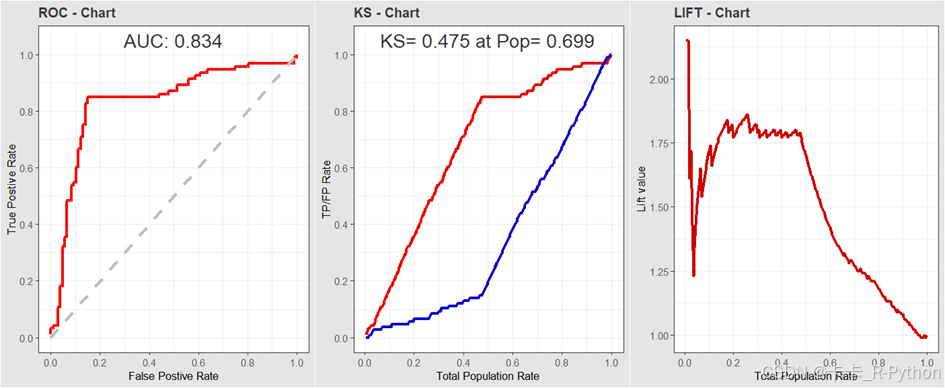

二、模型参数优化

1、训练集、验证集、测试集的引入

 ###   训练集、验证集、测试集的引入  ###  #注意：以下代码需要安装tensorflow和keras包才能运行  devtools::install_github("rstudio/tensorflow")  library(tensorflow)  install_tensorflow()  library(keras)  # 导入数据集  library(keras)  c(c(x_train,y_train),c(x_test,y_test )) %<-% dataset_mnist()  # 查看数据集的维度  cat('x_train shape:',dim(x_train))  cat('y_train shape:',dim(y_train))  cat('x_test shape:',dim(x_test))  cat('y_test shape:',dim(y_test))  # 对数字图像进行可视化  par(mfrow=c(3,3))  for(i in 1:9){    plot(as.raster(x_train[i,,],max = 255))    title(main = paste0('数字标签为：',y_train[i]))  }

par(mfrow = c(1,1))

 # 数据预处理  x_train <- array_reshape(x_train,c(nrow(x_train),784))  x_test <- array_reshape(x_test,c(nrow(x_test),784))  x_train <- x_train / 255  x_test <- x_test / 255  y_train <- to_categorical(y_train,10)  y_test <- to_categorical(y_test,10)    # 构建网络结构  model <- keras_model_sequential()  model %>%    layer_dense(units = 256,activation = 'relu',input_shape = c(784)) %>%    layer_dense(units = 128,activation = 'relu') %>%    layer_dense(units = 10,activation = 'softmax')  summary(model)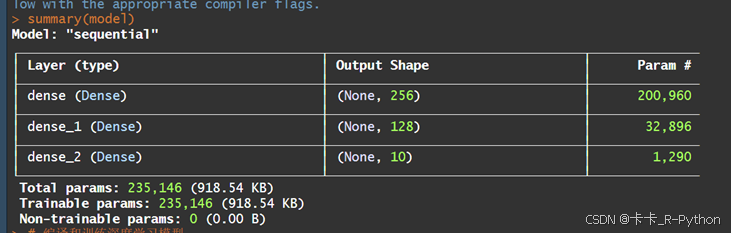

> # 编译和训练深度学习模型  > model %>%  +   compile(loss = 'categorical_crossentropy',  +           optimizer = optimizer_rmsprop(),  +           metrics = c('accuracy'))  > history <- model %>% fit(  +   x_train,y_train,  +   epochs = 10,batch_size = 128,  +   validation_split = 0.2  + )

Epoch 1/10

  1/375━━━━━━━━━━━━━━━━━━━━2:25 389ms/step - accuracy: 0.0547 - loss: 2.3528

 19/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.5331 - loss: 1.5280   

 39/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.6426 - loss: 1.2044

 60/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.6974 - loss: 1.0292

 80/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.7294 - loss: 0.9236

 99/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.7511 - loss: 0.8515

119/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.7683 - loss: 0.7934

140/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.7827 - loss: 0.7446

160/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.7938 - loss: 0.7066

179/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8028 - loss: 0.6759

201/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8117 - loss: 0.6454

220/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8185 - loss: 0.6224

240/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8247 - loss: 0.6009

261/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8305 - loss: 0.5809

282/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8357 - loss: 0.5630

303/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8404 - loss: 0.5468

323/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8445 - loss: 0.5327

344/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8484 - loss: 0.5191

363/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.8517 - loss: 0.5077

375/375━━━━━━━━━━━━━━━━━━━━2s 4ms/step - accuracy: 0.8538 - loss: 0.5004 - val_accuracy: 0.9590 - val_loss: 0.1390

Epoch 2/10

  1/375━━━━━━━━━━━━━━━━━━━━8s 22ms/step - accuracy: 0.9688 - loss: 0.1577

 19/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9593 - loss: 0.1446

 37/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9586 - loss: 0.1431

 55/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9581 - loss: 0.1421

 72/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9581 - loss: 0.1414

 92/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9581 - loss: 0.1412

111/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9580 - loss: 0.1407

130/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9582 - loss: 0.1397

150/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9585 - loss: 0.1387

171/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9587 - loss: 0.1377

191/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9589 - loss: 0.1367

211/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9592 - loss: 0.1358

230/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9594 - loss: 0.1349

250/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9596 - loss: 0.1340

269/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9598 - loss: 0.1332

291/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9601 - loss: 0.1322

311/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9603 - loss: 0.1314

331/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9605 - loss: 0.1307

352/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9607 - loss: 0.1300

372/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9609 - loss: 0.1293

375/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9610 - loss: 0.1292 - val_accuracy: 0.9680 - val_loss: 0.1072

Epoch 3/10

  1/375━━━━━━━━━━━━━━━━━━━━8s 23ms/step - accuracy: 0.9453 - loss: 0.1397

 21/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9727 - loss: 0.0838

 41/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9750 - loss: 0.0806

 59/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9759 - loss: 0.0788

 78/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9763 - loss: 0.0776

 99/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9764 - loss: 0.0771

119/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9765 - loss: 0.0770

139/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9764 - loss: 0.0773

161/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9764 - loss: 0.0776

183/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9763 - loss: 0.0778

205/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9763 - loss: 0.0778

224/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9763 - loss: 0.0778

244/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9764 - loss: 0.0777

264/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9764 - loss: 0.0777

282/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9764 - loss: 0.0776

301/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9765 - loss: 0.0775

319/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9765 - loss: 0.0774

337/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9765 - loss: 0.0773

356/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9765 - loss: 0.0773

375/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9766 - loss: 0.0772 - val_accuracy: 0.9735 - val_loss: 0.0908

Epoch 4/10

  1/375━━━━━━━━━━━━━━━━━━━━8s 24ms/step - accuracy: 0.9766 - loss: 0.0345

 22/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9827 - loss: 0.0557

 42/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9834 - loss: 0.0553

 63/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9832 - loss: 0.0555

 85/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9830 - loss: 0.0560

105/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9830 - loss: 0.0561

125/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9830 - loss: 0.0561

146/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9830 - loss: 0.0562

167/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9829 - loss: 0.0563

186/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9829 - loss: 0.0564

204/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9829 - loss: 0.0564

221/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9828 - loss: 0.0565

241/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9828 - loss: 0.0565

261/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9828 - loss: 0.0565

281/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9828 - loss: 0.0564

301/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9828 - loss: 0.0564

320/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9828 - loss: 0.0563

339/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9828 - loss: 0.0562

357/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9828 - loss: 0.0562

375/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9828 - loss: 0.0562 - val_accuracy: 0.9747 - val_loss: 0.0845

Epoch 5/10

  1/375━━━━━━━━━━━━━━━━━━━━7s 21ms/step - accuracy: 1.0000 - loss: 0.0048

 21/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9920 - loss: 0.0268

 41/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9910 - loss: 0.0300

 62/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9907 - loss: 0.0303

 82/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9904 - loss: 0.0309

102/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9900 - loss: 0.0317

122/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9897 - loss: 0.0325

142/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9895 - loss: 0.0333

163/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9893 - loss: 0.0339

183/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9892 - loss: 0.0344

203/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9890 - loss: 0.0350

223/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9889 - loss: 0.0354

244/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9888 - loss: 0.0359

262/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9887 - loss: 0.0362

280/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9886 - loss: 0.0366

300/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9885 - loss: 0.0369

321/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9884 - loss: 0.0372

341/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9883 - loss: 0.0375

360/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9883 - loss: 0.0377

375/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9882 - loss: 0.0379 - val_accuracy: 0.9728 - val_loss: 0.0921

Epoch 6/10

  1/375━━━━━━━━━━━━━━━━━━━━9s 25ms/step - accuracy: 1.0000 - loss: 0.0120

 20/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9924 - loss: 0.0235

 39/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9915 - loss: 0.0258

 58/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9911 - loss: 0.0267

 78/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9910 - loss: 0.0270

 99/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9908 - loss: 0.0273

118/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9907 - loss: 0.0277

138/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9907 - loss: 0.0280

157/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9906 - loss: 0.0284

175/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9905 - loss: 0.0288

194/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9904 - loss: 0.0291

213/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9904 - loss: 0.0294

233/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9903 - loss: 0.0296

254/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9903 - loss: 0.0298

275/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9903 - loss: 0.0300

296/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9903 - loss: 0.0302

317/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9902 - loss: 0.0303

337/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9902 - loss: 0.0305

358/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9902 - loss: 0.0306

375/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9902 - loss: 0.0307 - val_accuracy: 0.9768 - val_loss: 0.0857

Epoch 7/10

  1/375━━━━━━━━━━━━━━━━━━━━9s 25ms/step - accuracy: 1.0000 - loss: 0.0091

 20/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9955 - loss: 0.0147

 39/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9948 - loss: 0.0171

 58/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9946 - loss: 0.0183

 77/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9945 - loss: 0.0192

 95/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9944 - loss: 0.0196

114/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9944 - loss: 0.0197

133/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9943 - loss: 0.0199

154/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9943 - loss: 0.0201

175/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9941 - loss: 0.0203

195/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9940 - loss: 0.0206

216/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9939 - loss: 0.0208

237/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9938 - loss: 0.0211

258/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9937 - loss: 0.0213

278/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9936 - loss: 0.0215

299/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9935 - loss: 0.0218

319/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9934 - loss: 0.0220

339/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9933 - loss: 0.0222

359/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9933 - loss: 0.0223

375/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9932 - loss: 0.0225 - val_accuracy: 0.9763 - val_loss: 0.0927

Epoch 8/10

  1/375━━━━━━━━━━━━━━━━━━━━8s 22ms/step - accuracy: 1.0000 - loss: 0.0030

 21/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9955 - loss: 0.0162

 42/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9952 - loss: 0.0177

 62/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9950 - loss: 0.0180

 83/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9950 - loss: 0.0181

104/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9950 - loss: 0.0179

125/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9949 - loss: 0.0180

147/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9948 - loss: 0.0181

168/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9947 - loss: 0.0181

188/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9946 - loss: 0.0181

209/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9945 - loss: 0.0181

229/375━━━━━━━━━━━━━━━━━━━━0s 2ms/step - accuracy: 0.9945 - loss: 0.0182

247/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9945 - loss: 0.0182

265/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9944 - loss: 0.0182

284/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9944 - loss: 0.0182

303/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9944 - loss: 0.0183

322/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9944 - loss: 0.0183

341/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9943 - loss: 0.0183

358/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9943 - loss: 0.0184

375/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9943 - loss: 0.0184 - val_accuracy: 0.9790 - val_loss: 0.0842

Epoch 9/10

  1/375━━━━━━━━━━━━━━━━━━━━8s 24ms/step - accuracy: 1.0000 - loss: 0.0019

 20/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9972 - loss: 0.0090

 40/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9971 - loss: 0.0098

 60/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9970 - loss: 0.0100

 79/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9970 - loss: 0.0102

100/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9969 - loss: 0.0103

120/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9968 - loss: 0.0106

140/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9968 - loss: 0.0108

161/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9967 - loss: 0.0110

181/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9967 - loss: 0.0111

201/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9967 - loss: 0.0113

222/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9967 - loss: 0.0114

242/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9966 - loss: 0.0116

260/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9965 - loss: 0.0117

277/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9965 - loss: 0.0118

298/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9964 - loss: 0.0119

319/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9964 - loss: 0.0121

340/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9963 - loss: 0.0122

360/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9963 - loss: 0.0124

375/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9962 - loss: 0.0125 - val_accuracy: 0.9783 - val_loss: 0.0885

Epoch 10/10

  1/375━━━━━━━━━━━━━━━━━━━━30s 82ms/step - accuracy: 1.0000 - loss: 0.0014

 20/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9981 - loss: 0.0071 

 40/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9973 - loss: 0.0084

 59/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9970 - loss: 0.0088

 78/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9970 - loss: 0.0090

 98/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9969 - loss: 0.0093

118/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9969 - loss: 0.0094

137/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9969 - loss: 0.0096

156/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9968 - loss: 0.0098

176/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9967 - loss: 0.0100

195/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9967 - loss: 0.0101

215/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9966 - loss: 0.0102

236/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9966 - loss: 0.0103

256/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9966 - loss: 0.0105

276/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9965 - loss: 0.0106

296/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9965 - loss: 0.0106

316/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9965 - loss: 0.0107

335/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9965 - loss: 0.0107

354/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9965 - loss: 0.0107

374/375━━━━━━━━━━━━━━━━━━━━0s 3ms/step - accuracy: 0.9965 - loss: 0.0108

375/375━━━━━━━━━━━━━━━━━━━━1s 3ms/step - accuracy: 0.9965 - loss: 0.0108 - val_accuracy: 0.9798 - val_loss: 0.0888

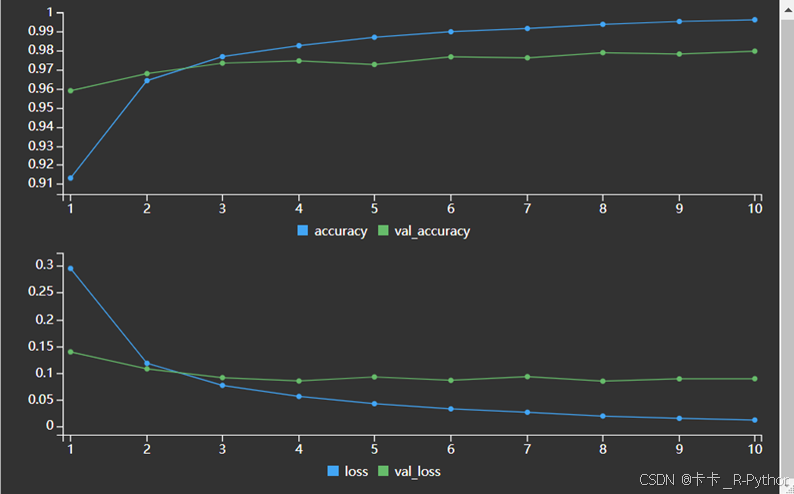
plot(history)

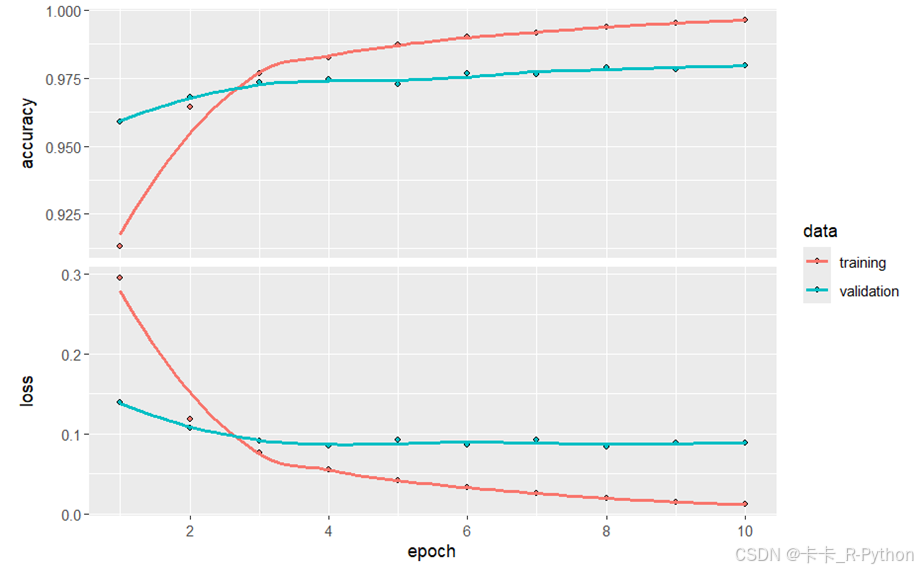
# 评估模型效果  DNN_score <- model %>% evaluate(x_test,y_test)  DNN_score$acc # 查看测试集的准确率

2、k折线交叉验证

### 10折交叉验证 ###  # 导入car数据集  car <- read.table("../data/car.data",sep = ",")  # 对变量重命名  colnames(car) <- c("buy","main","doors","capacity",                     "lug_boot","safety","accept")    # 手动构建10折交叉验证  #下面构造10折下标集  library(caret)  ind<-createFolds(car$accept,k=10,list=FALSE,returnTrain=FALSE)  # 下面再做10折交叉验证，这里仅给出训练集和测试集的分类平均误判率。  E0=rep(0,10);E1=E0  car$accept<-as.factor(car$accept)  library(C50)  for(i in 1:10){    n0=nrow(car)-nrow(car[ind==i,]);n1=nrow(car[ind==i,])    a=C5.0(accept~.,car[!ind==i,])    E0[i]=sum(car[!ind==i,'accept']!=predict(a,car[!ind==i,]))/n0    E1[i]=sum(car[ind==i,'accept']!=predict(a,car[ind==i,]))/n1  }  (1-mean(E0));(1-mean(E1))

# 利用caret包中的trainControl函数完成交叉验证  library(caret)  library(ROCR)  control <- trainControl(method="repeatedcv",number=10,repeats=3)  model <- train(accept~.,data=car,method="rpart",                 trControl=control)  model

plot(model)

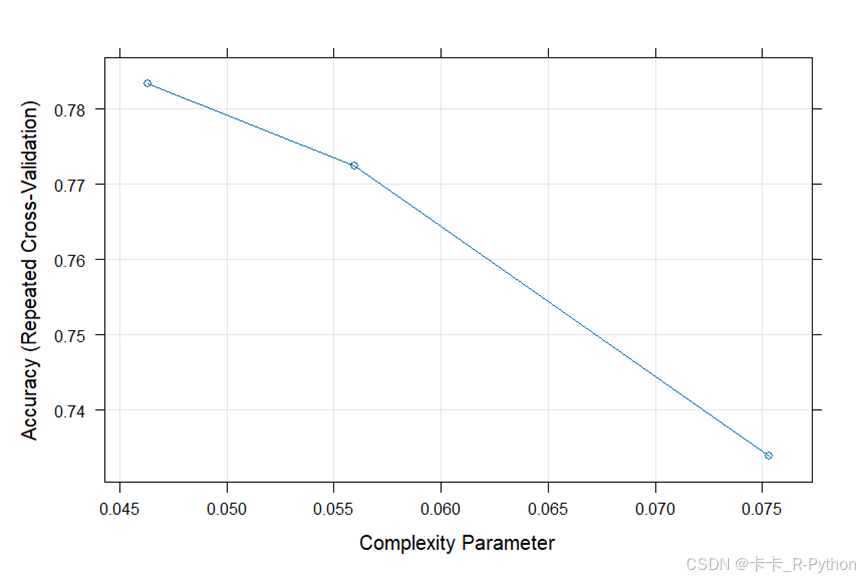
2、网格搜索

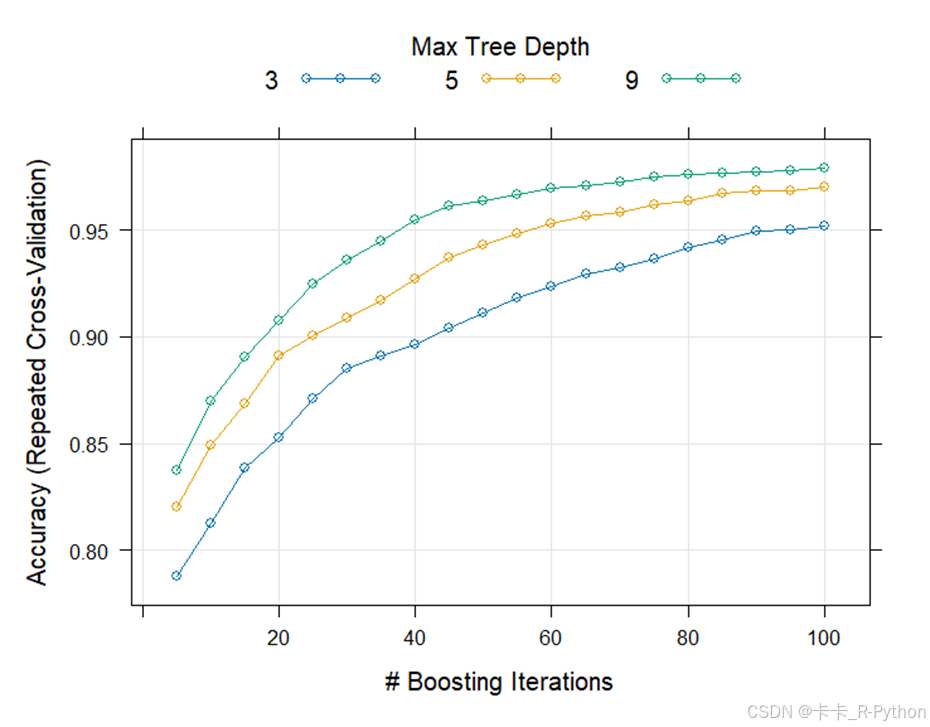
### 网格搜索 ###  ### 网格搜索 ###  #install.packages("gbm")  set.seed(1234)  library(caret)  library(gbm)fitControl <- trainControl(method = 'repeatedcv',                             number = 10,                             repeats = 5)  # 设置网格搜索的参数池  gbmGrid <- expand.grid(interaction.depth = c(3,5,9),                         n.trees = (1:20)*5,                         shrinkage = 0.1,                         n.minobsinnode = 20)  nrow(gbmGrid)

# 训练模型，找出最优参数组合  gbmfit <- train(accept ~ .,data = car,                  method = 'gbm',                  trControl = fitControl,                  tuneGrid = gbmGrid,                  metric = 'Accuracy')    gbmfit$bestTune # 查看模型最优的参数组合

plot(gbmfit)