阅读量:3
目录
前期试读,后续会将博客加入下列链接的专栏,欢迎订阅
Open3D点云算法与点云深度学习案例汇总(长期更新)-CSDN博客
一、概述
使用非线性最小二乘法拟合二维直线,可以通过优化算法来最小化点云数据与直线模型之间的误差。
1.1原理

1.2实现步骤
1.生成或读取点云数据:
使用 Open3D 生成或读取二维平面上的点云数据。
2.定义目标函数:
定义用于非线性最小二乘法优化的目标函数。
3.初始参数估计:
选择初始的圆心和半径估计值。
4.优化求解:
使用 scipy.optimize.least_squares 或其他优化算法进行非线性最小二乘法优化,拟合圆。
5.可视化结果:
使用 Open3D 可视化原始点云数据和拟合的圆。
二、代码实现
2.1关键函数
2.1.1定义残差函数
- 使用 residuals 函数计算圆拟合的残差。残差是每个点到圆周的距离减去圆的半径。
def residuals(params, points): """ 计算残差,用于非线性最小二乘法优化。 参数: params (numpy.ndarray): 圆的参数 (a, b, r)。 points (numpy.ndarray): 点云数据,形状为 (N, 2)。 返回: numpy.ndarray: 残差,形状为 (N,)。 """ a, b, r = params residuals = np.sqrt((points[:, 0] - a)**2 + (points[:, 1] - b)**2) - r return residuals2.1.2使用非线性最小二乘法拟合圆
- 使用 fit_circle_least_squares 函数进行非线性最小二乘法优化,拟合圆。初始参数估计使用点云数据的均值和平均距离。
def fit_circle_least_squares(points): """ 使用非线性最小二乘法拟合圆。 参数: points (numpy.ndarray): 点云数据,形状为 (N, 2)。 返回: tuple: 拟合的圆的参数 (a, b, r)。 """ # 初始参数估计 center_estimate = np.mean(points, axis=0) radius_estimate = np.mean(np.sqrt(np.sum((points - center_estimate)**2, axis=1))) initial_params = np.hstack((center_estimate, radius_estimate)) # 非线性最小二乘法优化 result = least_squares(residuals, initial_params, args=(points,)) return result.x2.2完整代码
import open3d as o3d import numpy as np from scipy.optimize import least_squares def generate_noisy_circle(center, radius, num_points=1000, noise_level=0.05): """ 生成带有噪声的二维圆形点云数据。 参数: center (tuple): 圆心的坐标 (a, b)。 radius (float): 圆的半径。 num_points (int): 点的数量。 noise_level (float): 噪声水平。 返回: numpy.ndarray: 生成的点云数据。 """ angles = np.linspace(0, 2 * np.pi, num_points) x = center[0] + radius * np.cos(angles) y = center[1] + radius * np.sin(angles) points = np.vstack((x, y)).T noise = np.random.normal(0, noise_level, points.shape) noisy_points = points + noise return noisy_points def residuals(params, points): """ 计算残差,用于非线性最小二乘法优化。 参数: params (numpy.ndarray): 圆的参数 (a, b, r)。 points (numpy.ndarray): 点云数据,形状为 (N, 2)。 返回: numpy.ndarray: 残差,形状为 (N,)。 """ a, b, r = params residuals = np.sqrt((points[:, 0] - a)**2 + (points[:, 1] - b)**2) - r return residuals def fit_circle_least_squares(points): """ 使用非线性最小二乘法拟合圆。 参数: points (numpy.ndarray): 点云数据,形状为 (N, 2)。 返回: tuple: 拟合的圆的参数 (a, b, r)。 """ # 初始参数估计 center_estimate = np.mean(points, axis=0) radius_estimate = np.mean(np.sqrt(np.sum((points - center_estimate)**2, axis=1))) initial_params = np.hstack((center_estimate, radius_estimate)) # 非线性最小二乘法优化 result = least_squares(residuals, initial_params, args=(points,)) return result.x def create_circle_mesh(center, radius, resolution=100): """ 创建一个圆的 Mesh,用于可视化。 参数: center (tuple): 圆心的坐标 (a, b)。 radius (float): 圆的半径。 resolution (int): 圆的分辨率。 返回: open3d.geometry.LineSet: 圆的 Mesh 对象。 """ angles = np.linspace(0, 2 * np.pi, resolution) x = center[0] + radius * np.cos(angles) y = center[1] + radius * np.sin(angles) z = np.zeros_like(x) circle_points = np.vstack((x, y, z)).T # 创建线框用于可视化圆 lines = [[i, (i + 1) % resolution] for i in range(resolution)] line_set = o3d.geometry.LineSet() line_set.points = o3d.utility.Vector3dVector(circle_points) line_set.lines = o3d.utility.Vector2iVector(lines) line_set.colors = o3d.utility.Vector3dVector([[1, 0, 0]] * len(lines)) # 红色 return line_set # 生成带有噪声的二维圆形点云数据 center = (0.0, 0.0) radius = 1.0 num_points = 1000 noise_level = 0.05 points = generate_noisy_circle(center, radius, num_points, noise_level) # 使用非线性最小二乘法拟合圆 fitted_params = fit_circle_least_squares(points) fitted_center = fitted_params[:2] fitted_radius = fitted_params[2] print(f"拟合的圆心: {fitted_center},拟合的半径: {fitted_radius}") # 创建点云对象 pcd = o3d.geometry.PointCloud() pcd.points = o3d.utility.Vector3dVector(np.c_[points, np.zeros(points.shape[0])]) # 创建拟合的圆的 Mesh 对象 circle_mesh = create_circle_mesh(fitted_center, fitted_radius) # 可视化点云和拟合的圆 o3d.visualization.draw_geometries([pcd, circle_mesh], window_name="Nonlinear Least Squares Circle Fitting", width=800, height=600, left=50, top=50) 三、实现效果
3.1拟合后点云
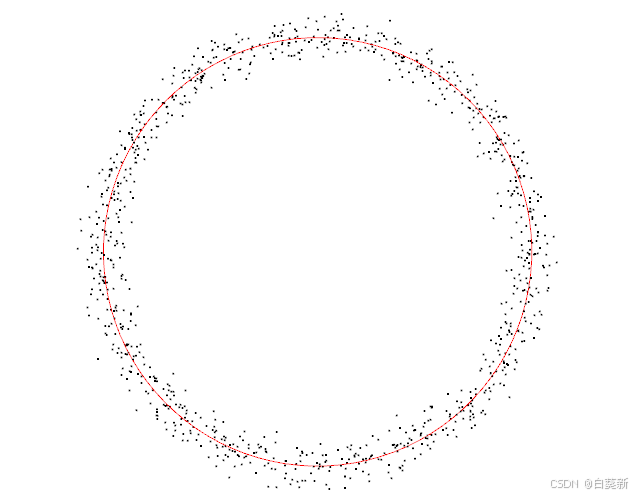
3.2结果数据
拟合的圆心: [-0.00028073 0.00063606],拟合的半径: 1.0012130828880563