动态规划
一、背包问题
① 01背包朴素版
算法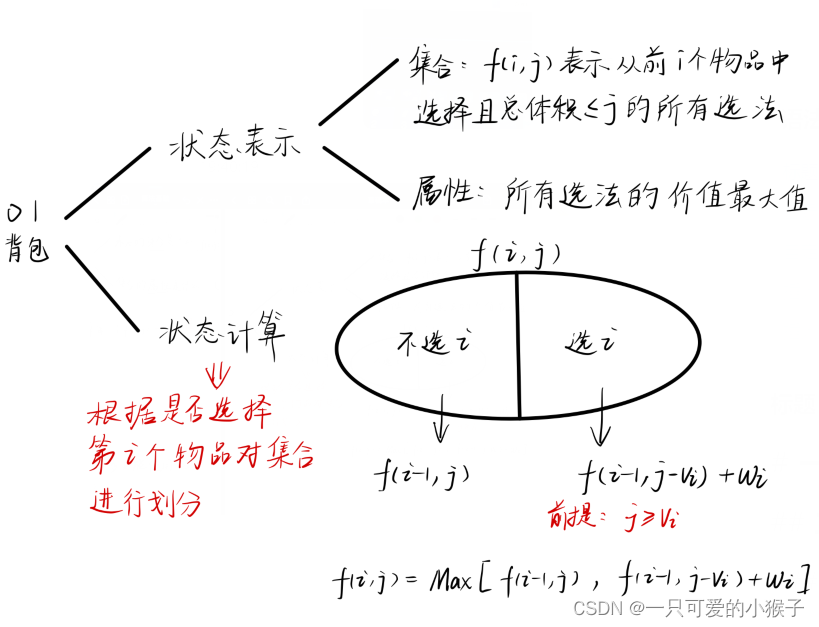
复杂度
时间复杂度0(nm)
空间复杂度0(nv)
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n, m; int v[N], w[N]; int f[N][N]; int main() { cin >> n >> m; for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i]; for (int i = 1; i <= n; i ++) //i == 0时,一件物品都不选,f都为0 { for (int j = 0; j <= m; j ++) { f[i][j] = f[i - 1][j]; //不包含第i个物品 if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); //包含第i个物品 } } cout << f[n][m]; //前n个物品中选择体积不超过m的最大价值 return 0; } ② 01背包优化版
算法
通过滚动数组对01背包朴素版进行空间上的优化
f[i] 与 f[i - 1]轮流交替
若体积从小到大进行遍历,当更新f[i, j]时,f[i - 1, j - vi] 已经在更新f[i, j - vi]时被更新了
因此体积需要从大到小进行遍历,当更新f[i, j]时,f[i - 1, j - vi] 还未被更新
复杂度
时间复杂度0(nm)
空间复杂度0(m)
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n, m; int v[N], w[N]; int f[N]; int main() { cin >> n >> m; for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i]; for (int i = 1; i <= n; i ++) //i == 0时,一件物品都不选,f都为0 { for (int j = m; j >= v[i]; j --) { f[j] = max(f[j], f[j - v[i]] + w[i]); //包含第i个物品 } } cout << f[m]; //前n个物品中选择体积不超过m的最大价值 return 0; } ③ 完全背包朴素版
算法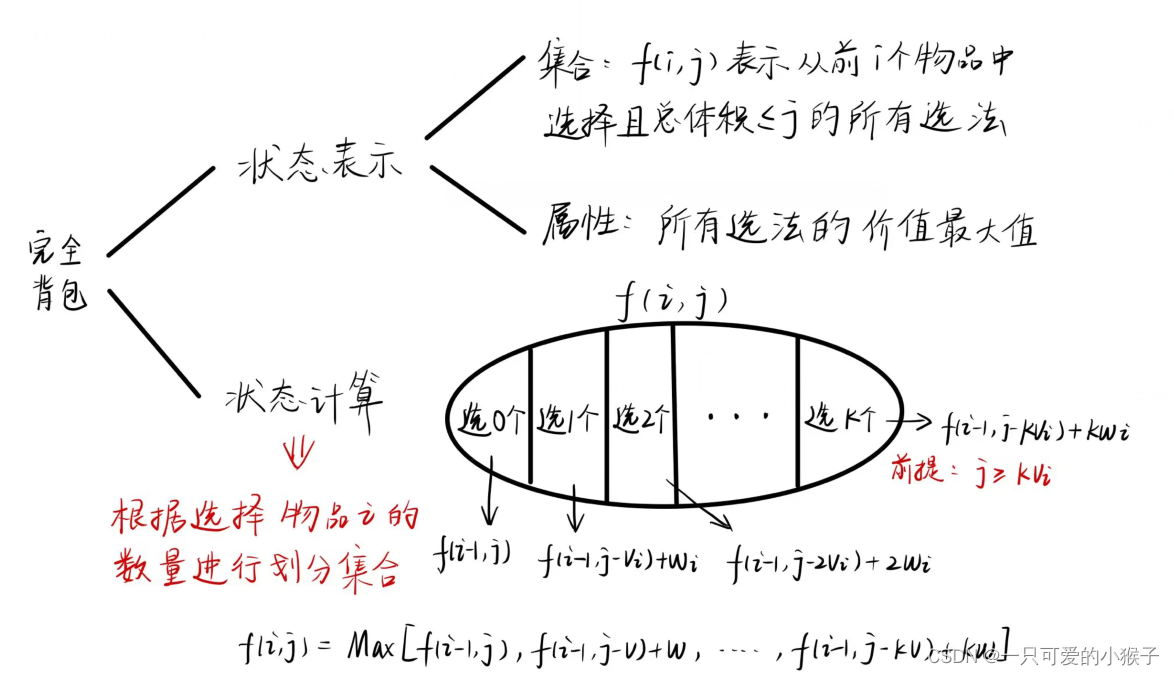
复杂度
时间复杂度:0(nm^2)
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n, m; int v[N], w[N]; int f[N][N]; int main() { cin >> n >> m; for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i]; for (int i = 1; i <= n; i ++) { for (int j = 0; j <= m; j ++) { for (int k = 0; k * v[i] <= j; k ++) { f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]); } } } cout << f[n][m]; return 0; } ④ 完全背包消k版
算法
f[i,j] = max(f[i-1, j], f[i-1, j-v]+w, f[i-1, j-2v]+2w…f[i-1, j-kv]+kw)
f[i, j-v] = max( f[i-1, j-v ], f[i-1, j-2v]+w … f[i-1, j-kv]+(k-1)w)
将f[i,j]优化成f[i,j] = max(f[i-1, j], f[i, j-v])
复杂度
由于不需要枚举选取物品i的数量
因此减少一轮迭代
0(nm)
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n, m; int v[N], w[N]; int f[N][N]; int main() { cin >> n >> m; for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i]; for (int i = 1; i <= n; i ++) { for (int j = 0; j <= m; j ++) { f[i][j] = f[i - 1][j]; //不选第i件物品 if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]); //选第i件物品 } } cout << f[n][m]; return 0; } ⑤ 完全背包消k优化版
算法
类比与01背包的滚动数组优化
将f[i]与f[i - 1]轮流交替使用数组进行存储
由于不存在01背包中的更新覆盖的情况
因此体积从小到大枚举即可
复杂度
空间复杂度0(NM) -> 0(M)
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n, m; int v[N], w[N]; int f[N]; int main() { cin >> n >> m; for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i]; for (int i = 1; i <= n; i ++) { for (int j = v[i]; j <= m; j ++) { f[j] = max(f[j], f[j - v[i]] + w[i]); } } cout << f[m]; return 0; } ⑥ 多重背包朴素版
算法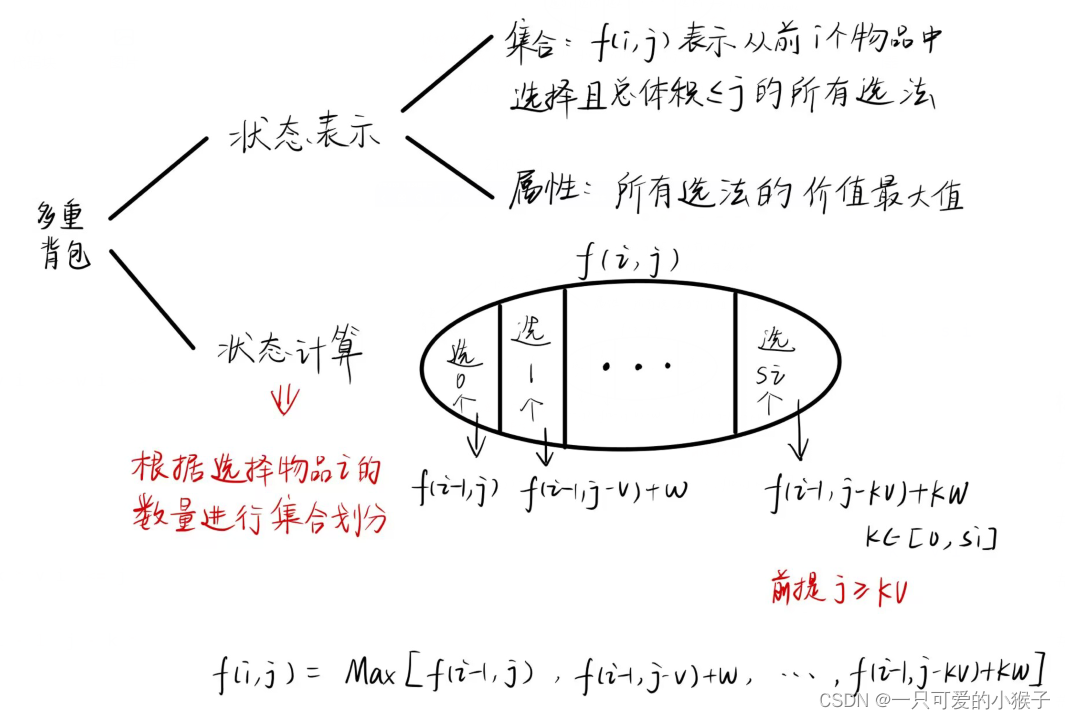
复杂度
时间复杂度:0(nm^2)
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 110; int n, m; int v[N], w[N], s[N]; int f[N][N]; int main() { cin >> n >> m; for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i] >> s[i]; for (int i = 1; i <= n; i ++) { for (int j = 0; j <= m; j ++) { for (int k = 0; k <= s[i] && k * v[i] <= j; k ++) { f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]); //相当于就是有个数限制的完全背包问题 } } } cout << f[n][m]; return 0; } ⑦多重背包二进制优化版
算法
每个物品可选[0, s]个,朴素版需要从0到s进行枚举
使用二进制进行优化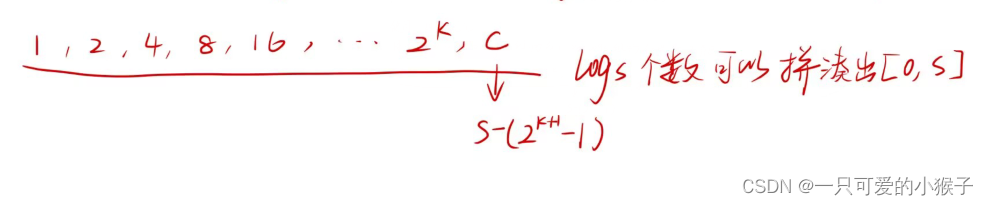
将si种选法分解成logs种选法,将所有选法重新存储起来
采用01背包的做法即可得到最优解
复杂度
时间复杂度0(nm)
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 22000, M = 2020; int n, m; int v[N], w[N]; int f[M]; int main() { cin >> n >> m; int cnt = 0; for (int i = 1; i <= n; i ++) //划分为二进制组 { int a, b, c; cin >> a >> b >> c; int k = 1; while (k <= c) { cnt ++; v[cnt] = k * a; w[cnt] = k * b; c -= k; k *= 2; } if (c > 0) { cnt ++; v[cnt] = c * a; w[cnt] = c * b; } } n = cnt; for (int i = 1; i <= n; i ++) //01背包 { for (int j = m; j >= v[i]; j --) { f[j] = max(f[j], f[j - v[i]] + w[i]); } } cout << f[m]; return 0; } ⑧ 分组背包朴素版
算法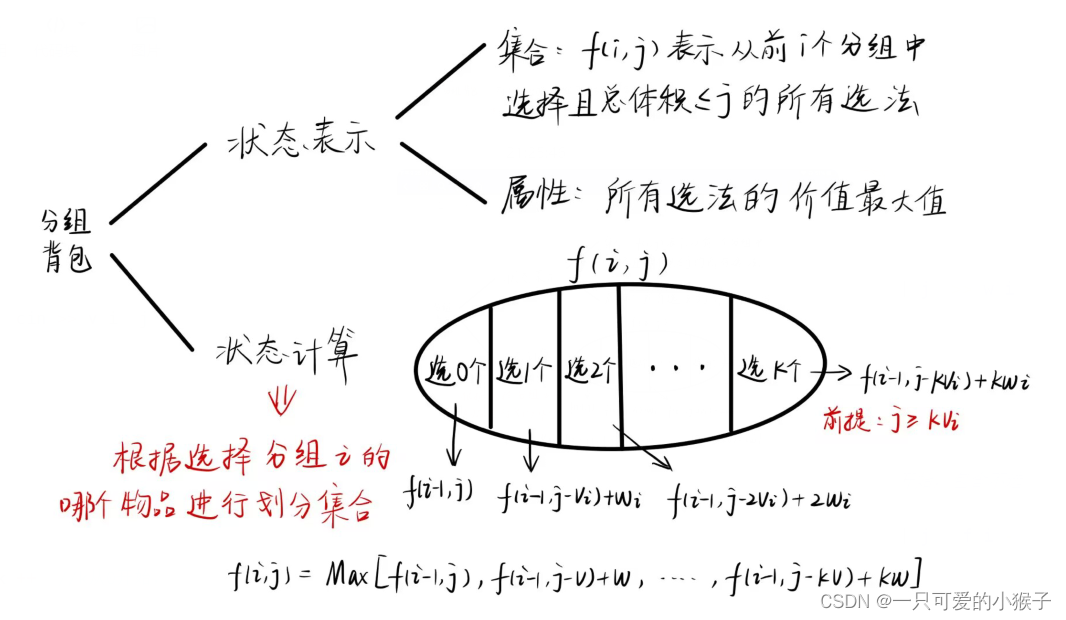
枚举每一个分组内的物品,进行01背包的选法策略
复杂度
时间复杂度0(nms)
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 110; int n, m; int v[N][N], w[N][N], s[N]; int f[N][N]; int main() { cin >> n >> m; for (int i = 1; i <= n; i ++) { cin >> s[i]; for (int j = 1; j <= s[i]; j ++) cin >> v[i][j] >> w[i][j]; } for (int i = 1; i <= n; i ++) { for (int j = 0; j <= m; j ++) { for (int k = 0; k <= s[i]; k ++) //k从0开始,包含不选该分组的f(i - 1, j) { if (j >= v[i][k]) f[i][j] = max(f[i][j], f[i - 1][ j - v[i][k]] + w[i][k]); //01背包 } } } cout << f[n][m]; return 0; } ⑨ 分组背包优化版
算法
采用01背包的滚动数组优化法
#include <iostream> #include <algorithm> using namespace std; const int N = 110; int n, m; int v[N][N], w[N][N], s[N]; int f[N]; int main() { cin >> n >> m; for (int i = 1; i <= n; i ++) { cin >> s[i]; for (int j = 1; j <= s[i]; j ++) cin >> v[i][j] >> w[i][j]; } for (int i = 1; i <= n; i ++) { for (int j = m; j >= 0; j --) { for (int k = 0; k <= s[i]; k ++) //k从0开始,包含不选该分组的f(i - 1, j) { if (j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]); //01背包 } } } cout << f[m]; return 0; } 二、线性dp
① 数字三角形
算法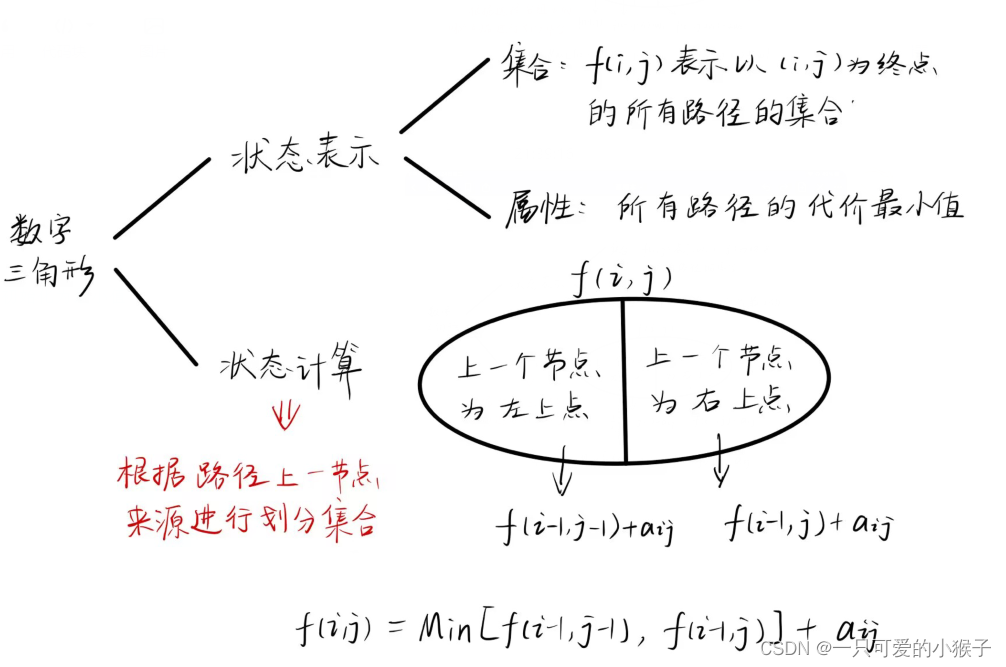
代码
#include <iostream> #include <algorithm> #include <cstring> using namespace std; const int N = 510, INF = 1e9; int n; int f[N][N]; int a[N][N]; int main() { cin >> n; for (int i = 0; i <= n; i ++) { for (int j = 0; j <= n; j ++) { f[i][j] = -INF; //将状态全部初始化为最小值 } } for (int i = 1; i <= n; i ++) { for (int j = 1; j <= i; j ++) { cin >> a[i][j]; //输入三角形 } } f[1][1] = a[1][1]; for (int i = 2; i <= n; i ++) { for (int j = 1; j <= i; j ++) { f[i][j] = max(f[i - 1][j], f[i - 1][j - 1]) + a[i][j]; } } int res = -INF; for (int i = 1; i <= n; i ++) res = max(res, f[n][i]); cout << res; return 0; } ② 最长上升子序列
算法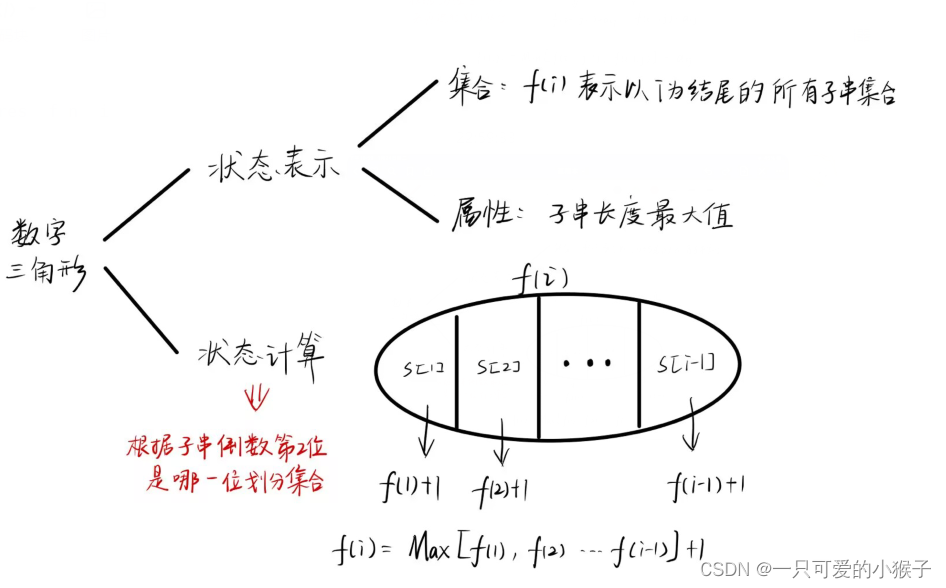
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n; int a[N]; int f[N]; int main() { cin >> n; for (int i = 1; i <= n; i ++) cin >> a[i]; for (int i = 1; i <= n; i ++) { f[i] = 1; for (int j = 1; j < i; j ++) { if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1); } } int res = 0; for (int i = 1; i <= n; i ++) res = max(res, f[i]); cout << res; return 0; } ③ 最长上升子序列打印序列版
算法
更新状态时,记录每一位子串是由哪一位结尾的子串转移而来的
再根据最大字串的末尾下标,倒序输出字串下标
#include <iostream> #include <algorithm> #include <stack> using namespace std; const int N = 1010; int n; int a[N]; int f[N]; int g[N];//保存以该位结尾的序列是由哪一位结尾的序列转移而来的 int main() { cin >> n; for (int i = 1; i <= n; i ++) cin >> a[i]; for (int i = 1; i <= n; i ++) { f[i] = 1; for (int j = 1; j < i; j ++) { if (a[j] < a[i]) { if (f[j] + 1 > f[i]) //更新f[i]是由f[j]转移过来的,并记录 { f[i] = f[j] + 1; g[i] = j; } } } } int k = 1; for (int i = 2; i <= n; i ++) { if (f[i] > f[k]) { k = i; } } cout << f[k] << endl; stack <int> s; for (int i = f[k]; i >= 1; i --) { s.push(k); //放入堆栈,可逆序输出 k = g[k]; } while (!s.empty()) { cout << a[s.top()] << " "; s.pop(); } return 0; } ④ 最长上升子序列0(nlogn)
算法
最长上升子序列的最后一位数,一定会随着长度的增长而严格单调增大
因此保存每一个长度的子序列的最小末位数
并枚举每一个数字,若以该数字结尾的序列,其倒数第二个数字应该是小于该数字的最大的数
因此在数组中二分倒数第二个数的位置
并更新数组
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 100010; int a[N]; int q[N]; int n; int main() { cin >> n; for (int i = 1; i <= n; i ++) cin >> a[i]; int len = 0; q[0] = -2e9; for (int i = 1; i <= n; i ++) { int l = 0, r = len; while (l < r) { int mid = l + r + 1 >> 1; if (q[mid] < a[i]) l = mid; else r = mid - 1; } len = max(len, r + 1); q[r + 1] = a[i]; } cout << len; return 0; } ⑤ 最长公共子序列
算法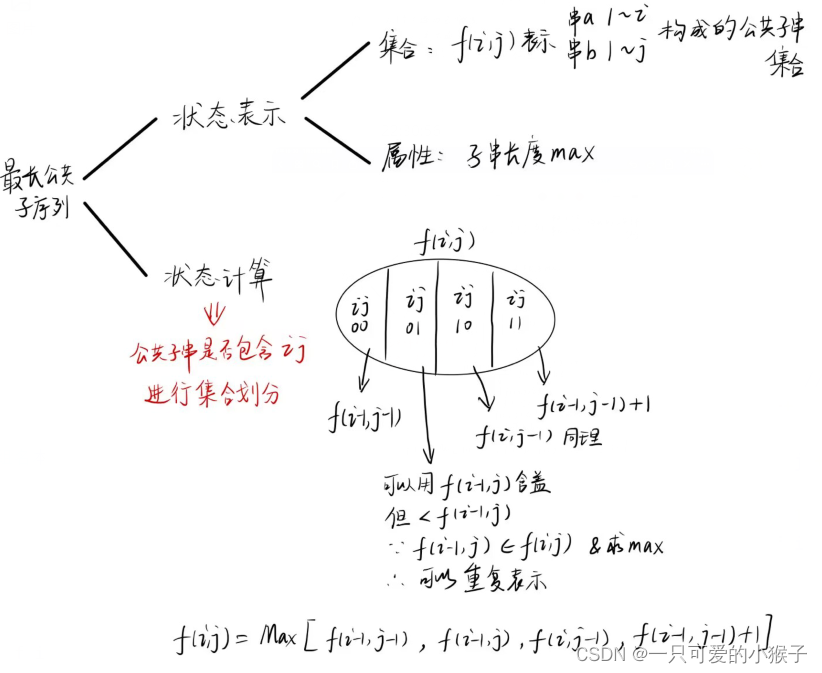
代码
#include <iostream> #include <algorithm> #include <cstring> using namespace std; const int N = 1010; int n, m; char a[N], b[N]; int f[N][N]; int main() { cin >> n >> m; scanf("%s%s", a + 1, b + 1); //写入a[0], b[0],数组名本身就是地址,不需要& for (int i = 1; i <= n; i ++) { for (int j = 1; j <= m; j ++) { f[i][j] = max(f[i - 1][j], f[i][j - 1]); if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1); //最长子序列包含a[i]/b[j] } } cout << f[n][m]; return 0; } ⑥ 最短编辑距离
算法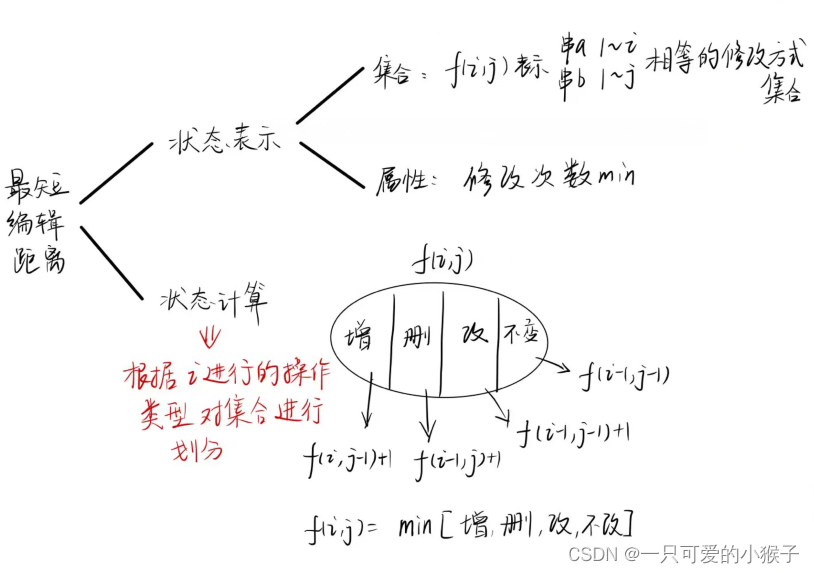
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int n, m; char a[N], b[N]; int f[N][N]; int main() { scanf("%d%s", &n, a + 1); scanf("%d%s", &m, b + 1); for (int i = 0; i <= n; i ++) f[i][0] = i; for (int i = 0; i <= m; i ++) f[0][i] = i; for (int i = 1; i <= n; i ++) { for (int j = 1; j <= m; j ++) { f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1); f[i][j] = min(f[i][j], f[i- 1][j - 1] + (a[i] != b[j])); } } cout << f[n][m]; return 0; } 三、区间dp(石子合并)
算法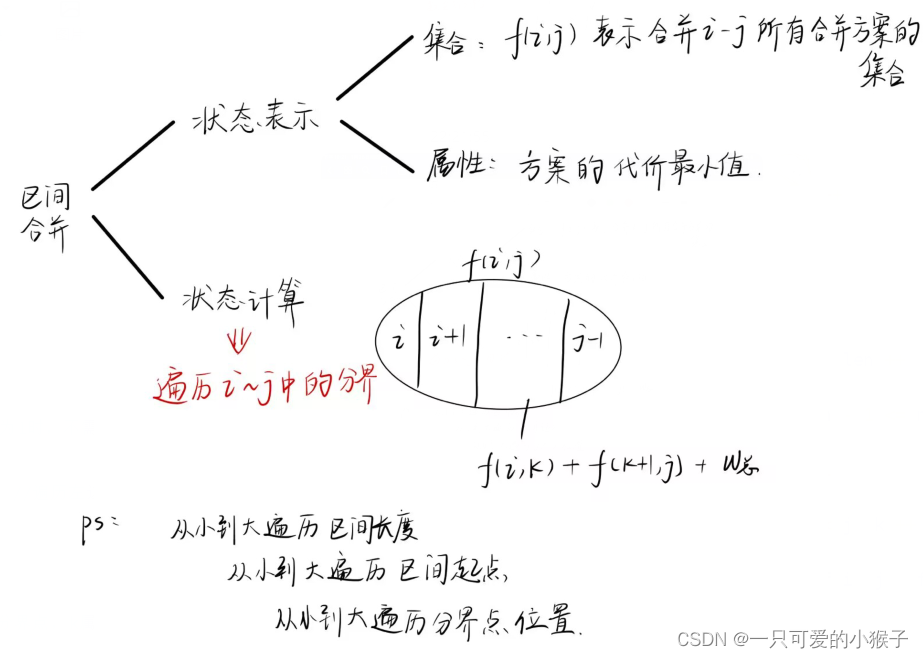
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 310, INF = 1e8; int f[N][N]; int s[N]; int a[N]; int n; int main() { cin >> n; for (int i = 1; i <= n; i ++) { cin >> a[i]; s[i] = a[i] + s[i - 1]; } for (int len = 2; len <= n; len ++) //当len为1时,不需要合并 { for (int i = 1; i + len - 1 <= n; i ++) //遍历左边界,左边界 + 长度不能越界 { int j = i + len - 1; f[i][j] = INF; for (int k = i; k < j; k ++) //遍历分界点,k属于[i,j - 1] { f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]); } } } cout << f[1][n]; return 0; } 四、计数类dp(整数划分)
- 完全背包解法
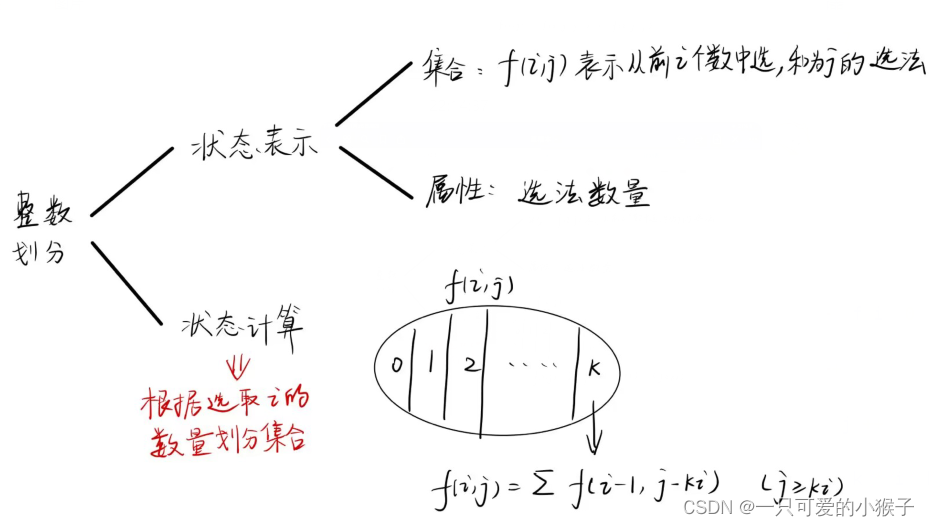
#include <iostream> #include <algorithm> using namespace std; const int N = 1010, mod = 1e9 + 7; int n; long long res; long long f[N][N]; int main() { cin >> n; for (int i = 0; i<= n; i ++) f[i][0] = 1; for (int i = 1; i <= n; i ++) { for (int j = 1; j <= n; j ++) { for (int k = 0; j >= k * i; k ++) { f[i][j] += f[i - 1][j - k * i] % mod; } } } cout << f[n][n]; return 0; } - 计数dp解法
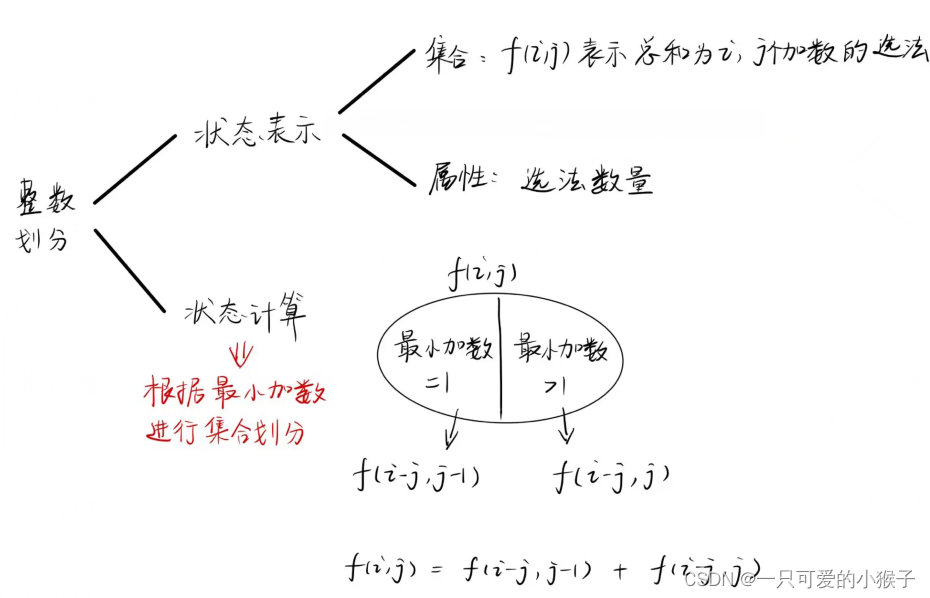
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; const long long mod = 1e9 + 7; int n; long long f[N][N]; int main() { cin >> n; f[0][0] = 1; //使得总和恰好为0,选择0个数的方案只有一种 for (int i = 1; i <= n; i ++) { for (int j = 1; j <= i; j ++) { f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod; } } long long res = 0; for (int i = 1; i <= n; i ++) res = (f[n][i] + res) % mod; cout << res; return 0; } 五、数位统计dp(计数问题)还没写
六、状态压缩dp
①蒙德里安的梦想
算法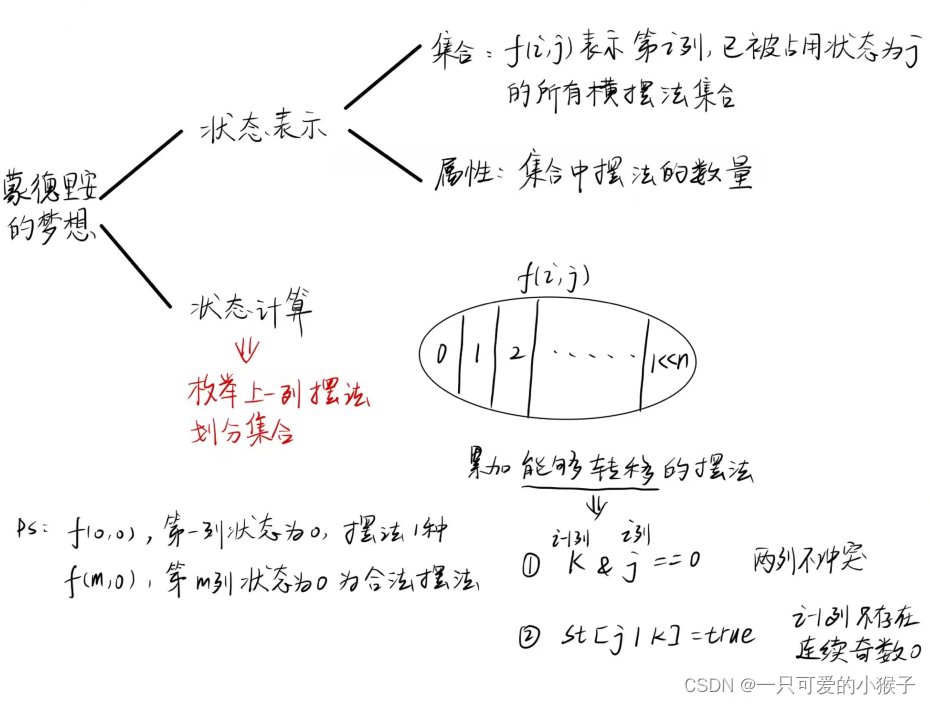
代码
#include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 12, M = 1 << N; int n, m; long long f[N][M]; bool st[M]; int main() { while (cin >> n >> m, n || m) { //初始化状态数组 memset(f, 0, sizeof(f)); //初始化判断是否有连续个奇数0的数组 for (int i = 0; i < 1 << n; i ++) { int cnt = 0; st[i] = true; for (int j = 0; j < n; j ++) { if ((i >> j) & 1) { if (cnt & 1) st[i] = false; cnt = 0; } else cnt ++; } if (cnt & 1) st[i] = false; } f[0][0] = 1; for (int i = 1; i <= m; i ++) { for (int j = 0; j < 1 << n; j ++) { for (int k = 0; k < 1 << n; k ++) { if (((j & k) == 0) && st[j | k]) f[i][j] += f[i - 1][k]; } } } cout << f[m][0] << endl; } return 0; } ②最短哈密顿路径
算法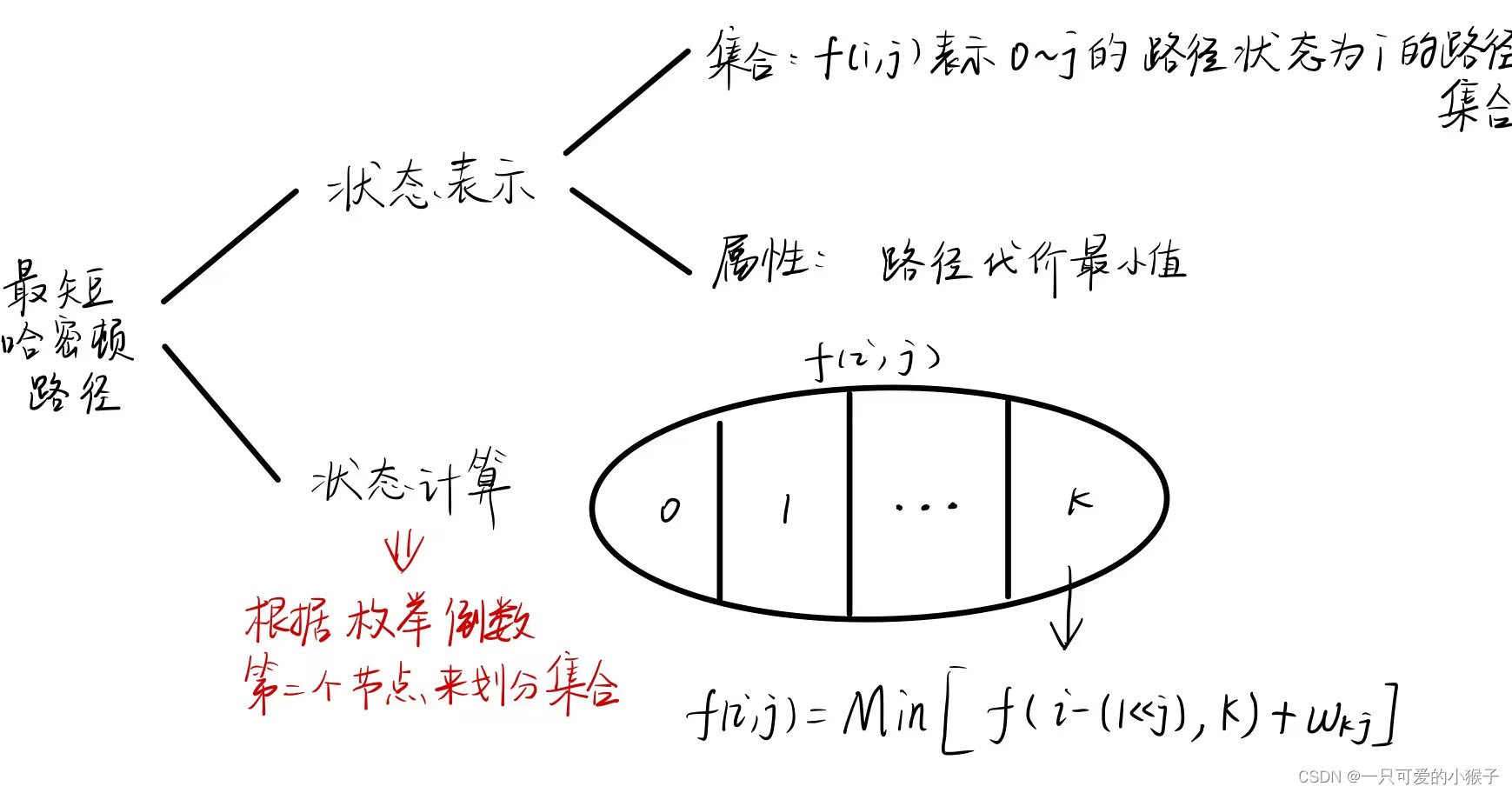
代码
#include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 20, M = 1 << N; int f[M][N]; int w[N][N]; int n; int main() { cin >> n; for (int i = 0; i < n; i ++) { for (int j = 0; j < n; j ++) { cin >> w[i][j]; } } memset(f, 0x3f, sizeof(f)); f[1][0] = 0; for (int i = 0; i < 1 << n; i ++) { for (int j = 0; j < n; j ++) { if ((i >> j) & 1) { for (int k = 0; k < n; k ++) { if (((i - (1 << j)) >> k) & 1) { f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]); } } } } } cout << f[(1 << n) - 1][n - 1]; return 0; } 七、树形dp(没有上司的舞会)
算法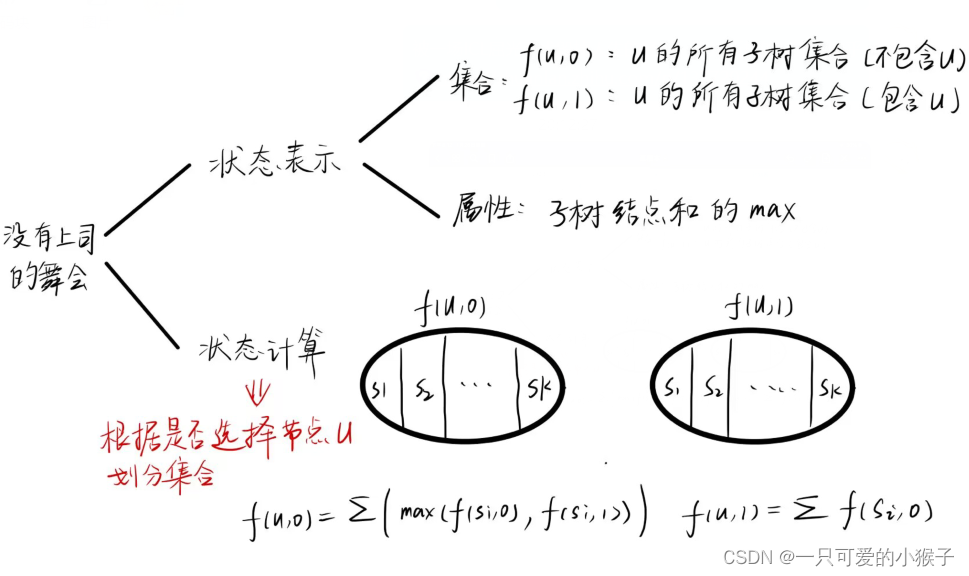
代码
#include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 6010; int f[N][2]; int happy[N]; bool has_father[N]; int h[N], e[N], ne[N], idx; int n; void add(int a, int b) //将子节点a加入到父节点b后 { e[idx] = a; ne[idx] = h[b]; h[b] = idx ++; } void dfs(int u) { f[u][1] = happy[u]; for (int i = h[u]; i != -1; i = ne[i]) { int j = e[i]; dfs(j); f[u][1] += f[j][0]; //包含u,则必不包含u的子节点 f[u][0] += max(f[j][0], f[j][1]); //不包含u,可以考虑包含u的子节点 } } int main() { cin >> n; for (int i = 1; i <= n; i ++) cin >> happy[i]; memset(h, -1, sizeof(h)); for (int i = 1; i < n; i ++) { int a, b; cin >> a >> b; has_father[a] = true; add(a, b); } int root = 1; while (has_father[root]) root ++; dfs(root); cout << max(f[root][0], f[root][1]); return 0; } 八、记忆化搜索(滑雪)
算法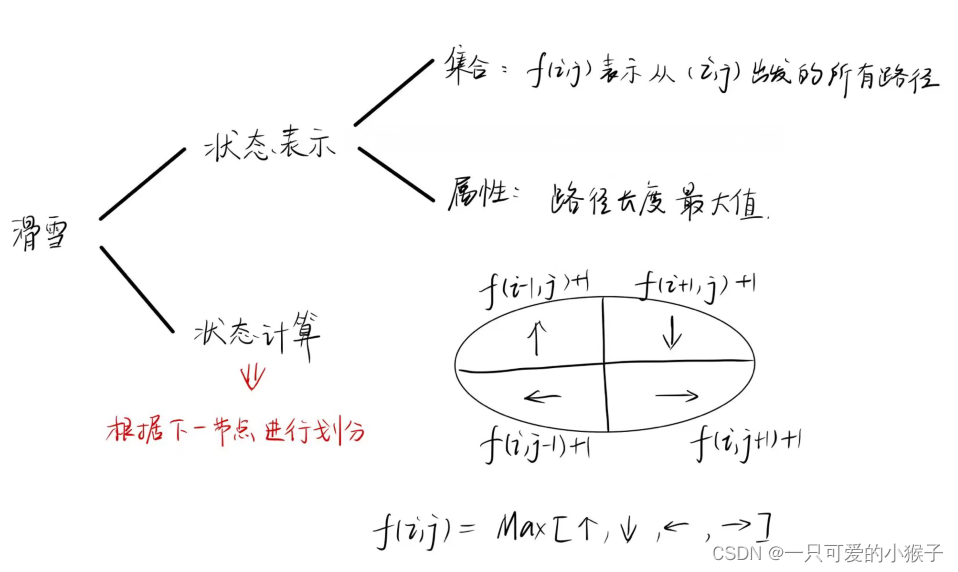
代码
#include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 310; int d[N][N]; int f[N][N]; int n, m; int dx[4] = {-1, 1, 0, 0}; int dy[4] = {0, 0, -1, 1}; int dp(int x, int y) { if (f[x][y] != -1) return f[x][y]; f[x][y] = 1; for (int i = 0; i < 4; i ++) { int a = x + dx[i], b = y + dy[i]; if (a >= 0 && a < n && b >= 0 && b < m && d[a][b] < d[x][y]) f[x][y] = max(f[x][y], dp(a, b) + 1); } return f[x][y]; } int main() { cin >> n >> m; for (int i = 0; i < n; i ++) { for (int j = 0; j < m; j ++) { cin >> d[i][j]; } } int res = 0; memset(f, -1, sizeof(f)); for (int i = 0; i < n; i ++) { for (int j = 0; j < m; j ++) { res = max(res, dp(i, j)); } } cout << res; return 0; } 