颠仆流离学二叉树1 （Java版）

avatar
作者
猴君
阅读量:1

本篇会加入个人的所谓鱼式疯言

❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言

而是理解过并总结出来通俗易懂的大白话,

小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的.

🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人能接受我们这个概念 ！！！

在这里插入图片描述

前言

学完了神奇的 栈和队列 ， 接下来要来到我们 歇斯底里，颠仆流离的 二叉树 环节 ， 相信学过 二叉树的 小伙伴，应该 对这个数据结构不陌生吧 ， 是不是恐怖如斯 啊， 下面就让我们看看它到底有多恐怖吧 💥 💥 💥

目录

  1. 树的初识

  2. 二叉树的初识

  3. 二叉树的特性以及应用

  4. 二叉树的存储

一. 树的初识

1. 树是概念

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。

把它叫做树是因为它看起来像一棵 倒挂的树，也就是说它是 根朝上 ，而 叶朝下的 。它具有以下的特点：

  • 有一个特殊的结点，称为 根结点 ，根结点没有 前驱结点

  • 除根结点外，其余结点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm，其中每一个 集合Ti (1 <= i <=m) 又是一棵 与树类似的 子树。每棵子树的根结点 有且只有一个前驱，可以有0个或多个后继

  • 树是 递归 定义的。`

在这里插入图片描述

在这里插入图片描述

注意：树形结构中，子树之间不能有交集，否则就不是树形结构

2. 树的结构

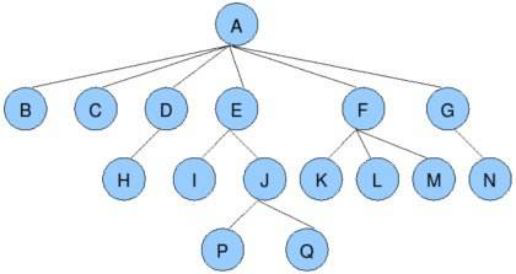
在这里插入图片描述

节点的度 ： 一个节点含有子树的个数称为该节点的度； 如上图 ： A 的度为 6

树的度： 一棵树中， 所有节点度的最大值为数的度； 如上图 ： 树 的度为 6

叶子节点和终端节点： 度为0的节点称为 叶子节点 ： 如上图 ： B , C , H , I , P , Q , K , L , M , N

双亲节点和父节点 ： 若一个节点含有子节点 ，则这个节点称为其子节点 的父节点 ; 如上图 ：A 是 B 的 父节点

孩子节点或子节点 ： 一个节点含有的 子树 的根节点称为该节点的子节点; 如上图： B 是 A 的孩子节点

根节点 ：一棵树中， 没有双亲节点的节点 ；如上图 ： A

节点的层次 : 从根开始定义起 ， 根为 第一层 ， 根的子节点为 第二层 ，以此类推

树的高度或深度：树中结点的最大层次； 如上图：树的深度为4， 也就是 最大高度 为 4

关于树的以下概念只需了解，在看书时只要知道是什么意思即可：

非终端结点或分支结点：度不为0的结点； 如上图：D、E、F、G…等节点为分支结点

兄弟结点：具有相同父结点的结点互称为兄弟结点； 如上图：B、C是兄弟结点

堂兄弟结点：双亲在同一层的结点互为堂兄弟；如上图：H、I互为兄弟结点

结点的祖先：从根到该结点所经分支上的所有结点；如上图：A是所有结点的祖先

子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是A的子孙

森林：由m（m>=0）棵互不相交的树组成的集合称为森林

鱼式疯言

于是我们总结了对于树概念的以下三点：

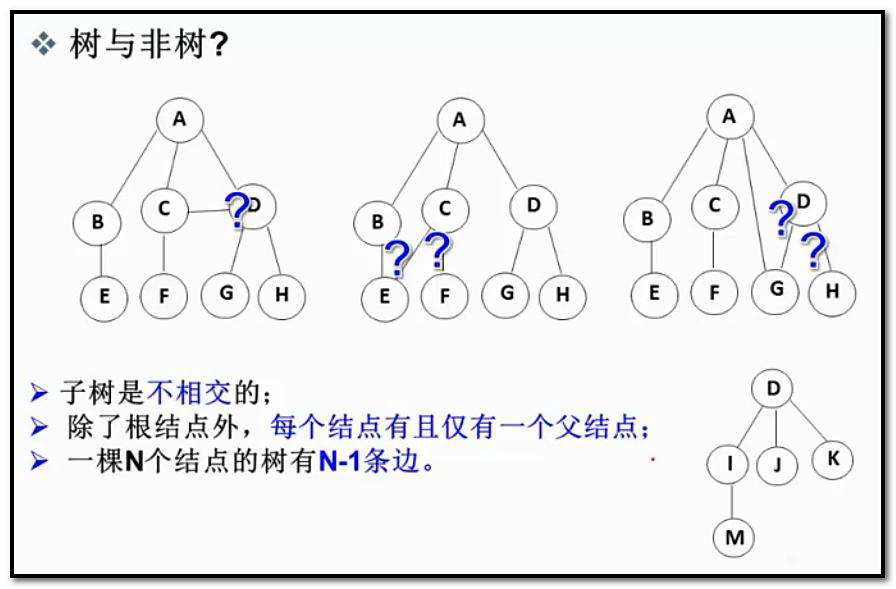
在这里插入图片描述

3. 树的表示形式

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，如：双亲表示法，
孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

class Node { int value; // 树中存储的数据 Node firstChild; // 第一个孩子引用 Node nextBrother; // 下一个兄弟引用 }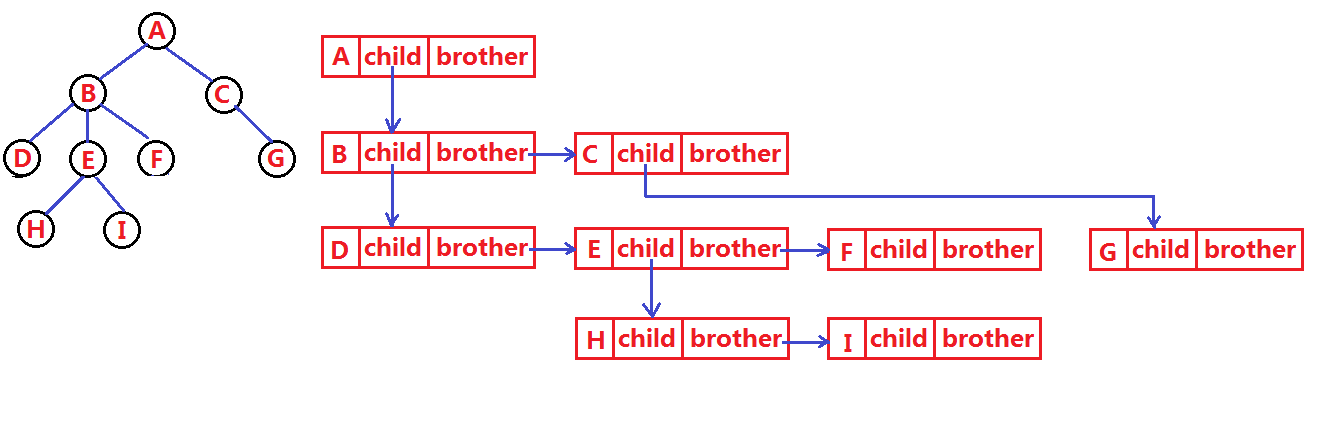

在这里插入图片描述

4. 树的应用

文件系统管理**（目录和文件）**

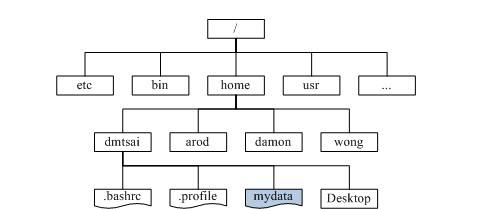
在这里插入图片描述

在这里插入图片描述

二. 二叉树

1. 二叉树的概念

一颗二叉树是节点的有限集合，该集合：

  1. 或者为空

  2. 或者是由一个根节点加上两颗称为 左子树 和 右子树 的二叉树组成

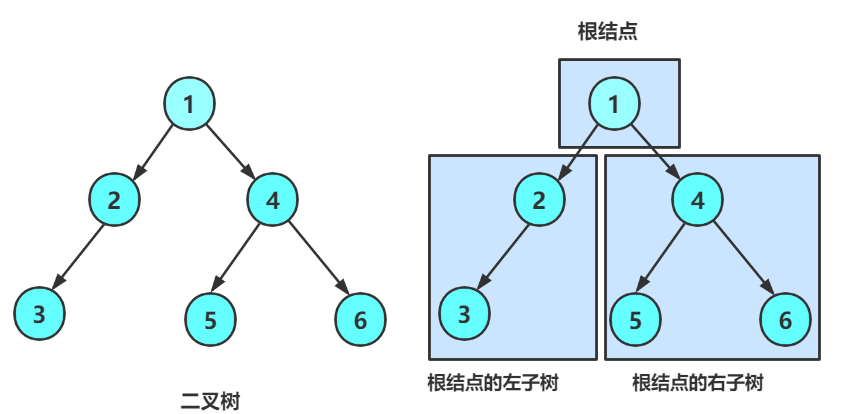
在这里插入图片描述

从上图可以看出

  1. 二叉树 不存在度大于 2 的节点

  2. 二叉树的字数有左子树和右子树之分，次序不能颠倒，因此 二叉树是有序树

所以我们可以得到以下 几种二叉树

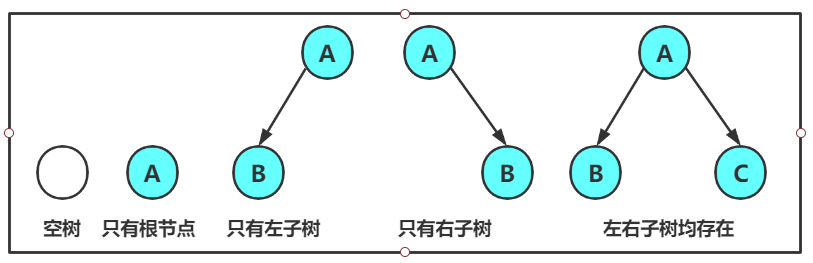
在这里插入图片描述

由此我们可以见识到大自然的 奇观

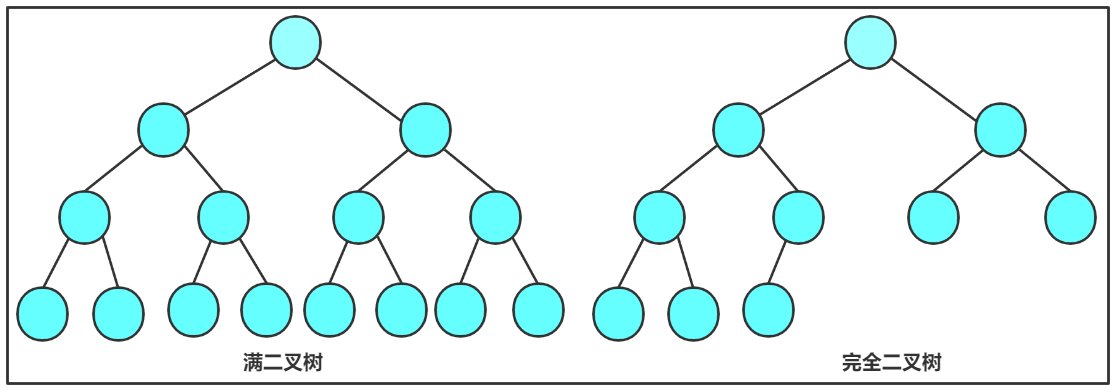
在这里插入图片描述

在这里插入图片描述

2. 二叉树的种类

  1. 满二叉树: 一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是 满二叉树。也就是说，如果一棵二叉树的层数为 K，且结点总数是 2^k-1，则它就是 满二叉树。

  2. 完全二叉树 : 完全二叉树 : 完全二叉树的是 效率很高 的数据结构， ，完全二叉树是由 满二叉树 而引出来的。对于 深度为K 的，有 n 个结点的 二叉树 ，当且仅当其 每一个结点都与深度为K 的满二叉树中编号从 0至n-1 的结点一一对应时称之为 完全二叉树 。

要注意的是满二叉树是一种 特殊的完全二叉树。

在这里插入图片描述

鱼式疯言

一句话来说就是

满二叉树就是每个节点度都为 2(除了叶子节点)

完全二叉树就是 从上往下数没有间断的节点，从左往右没有间断 的节点.

三. 二叉树的特性及应用

1. 二叉树的性质

  1. 若规定根结点的层数为 1，则一棵 非空二叉树的第 i 层 上最多有 2 ^ (i-1) (i>0) 个结点

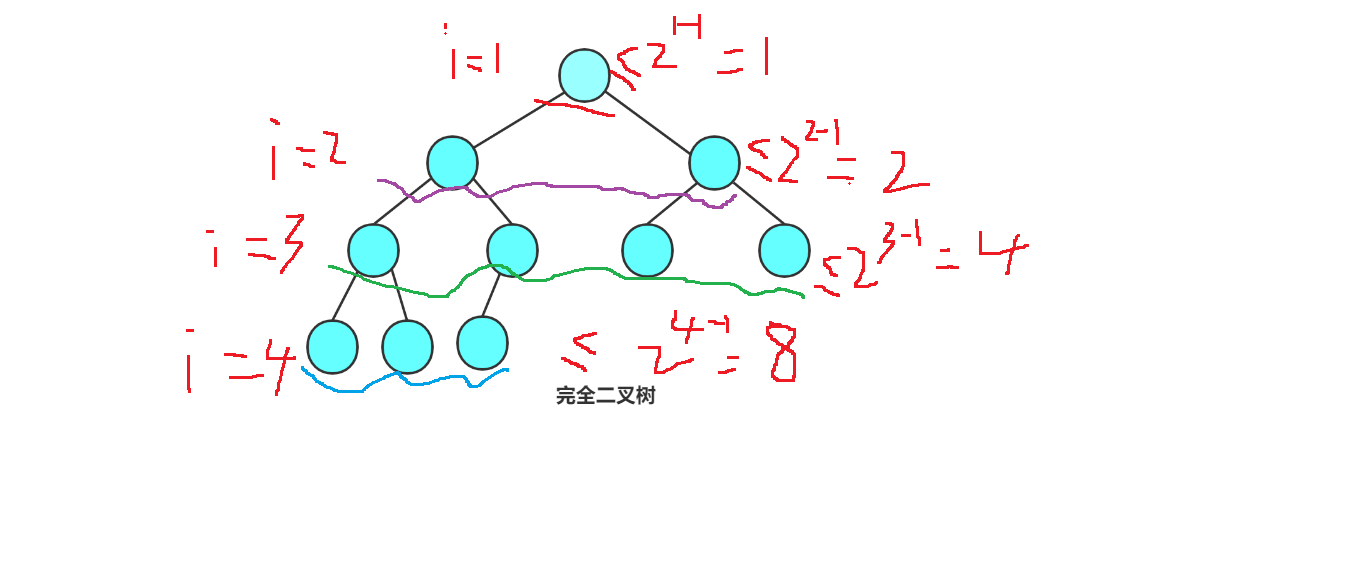
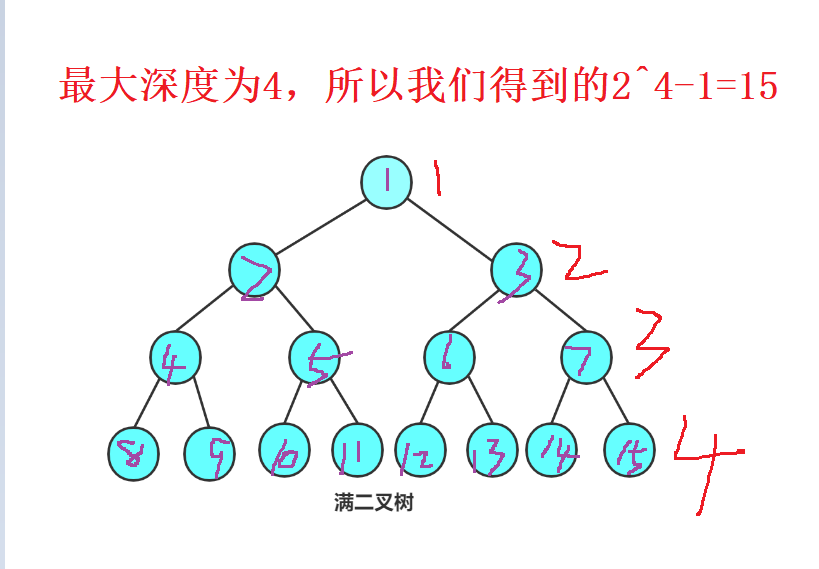
在这里插入图片描述

  1. 若规定只有根结点的二叉树的 深度为1 ，则深度为 K的二叉树的最大结点数是 2^K - 1 (k>=0)

在这里插入图片描述

  1. 对任何一棵二叉树, 如果其叶结点个数为 n0 , 度为 2 的非叶结点个数为 n2 ,则有 n0＝n2＋1

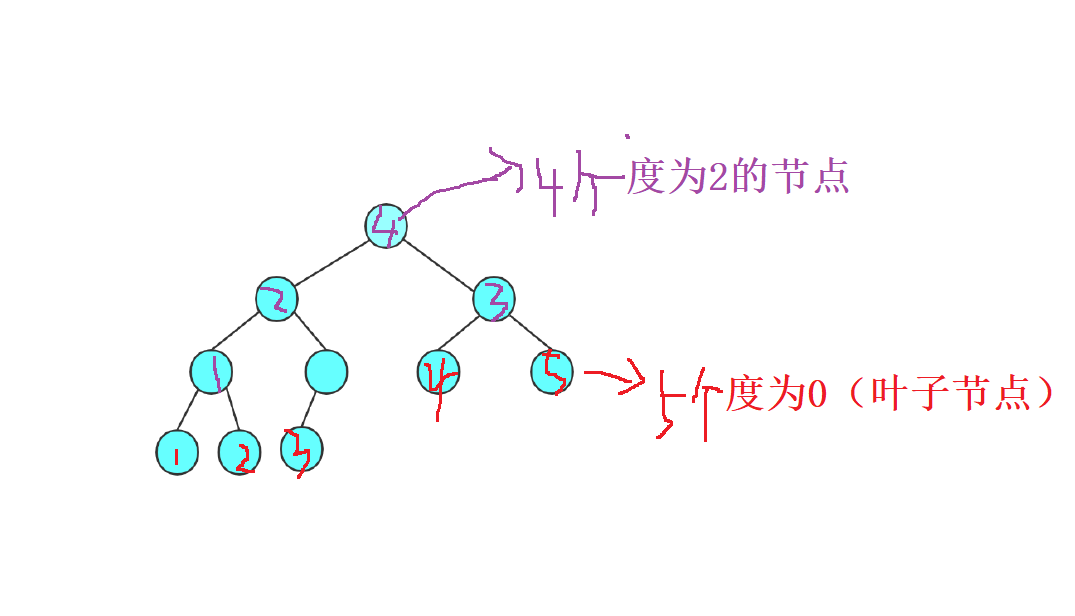
在这里插入图片描述

结论的推导过程 :

在这里插入图片描述

  1. 具有 n 个结点的 完全二叉树 的深度 k 为 log2（n+1 ）为上取整

在这里插入图片描述

什么？ 居然有人问我 向上取整 是什么 ？🤔 🤔 🤔

向上取整 的意思就是说，当这个数有小数的时候，就去掉 小数再 加1

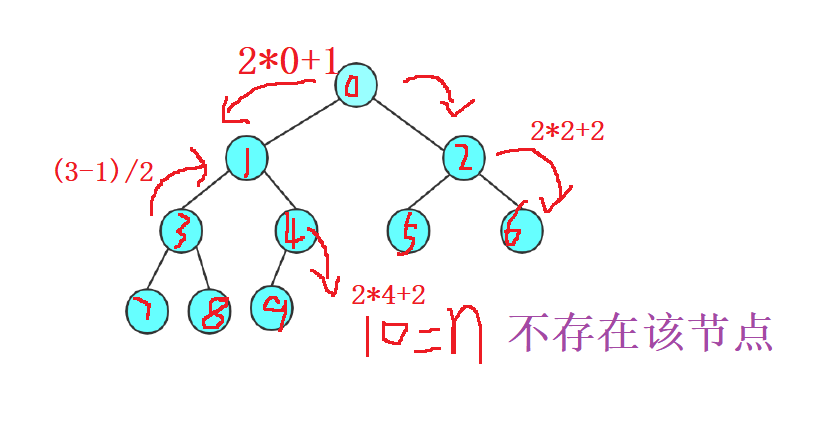
  1. 对于具有 n个结点 的完全二叉树，如果按照从上至下从左至右的顺序对所有节点 从 0开始编号 ，则对于 序号为 i 的结点有：

若 i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点

若 2i+1<n，左孩子序号：2i+1，否则无 左孩子

若 2i+2<n，右孩子序号：2i+2，否则无 右孩子

在这里插入图片描述

2. 二叉树性质的应用

题目一:

  1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）

A . 不存在这样的二叉树
B. 200
C. 198
D. 199

看到这题小伙伴是不是在心里窃喜呢 ， 没错

答案就是 200

解析： 直接套用 结论3 ： 域为 0 的节点 = 域为 2 的节点 +1

故选 B

题目二：

2.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）

A. n
B. n+1
C. n-1
D. n/2

本题呢，主要我们要结合是 完全二叉树 这个特点

要多利用 结论3 并要发现 当 总节点数为偶数 时， 就需要注意到 度为1 的节点只有 一个

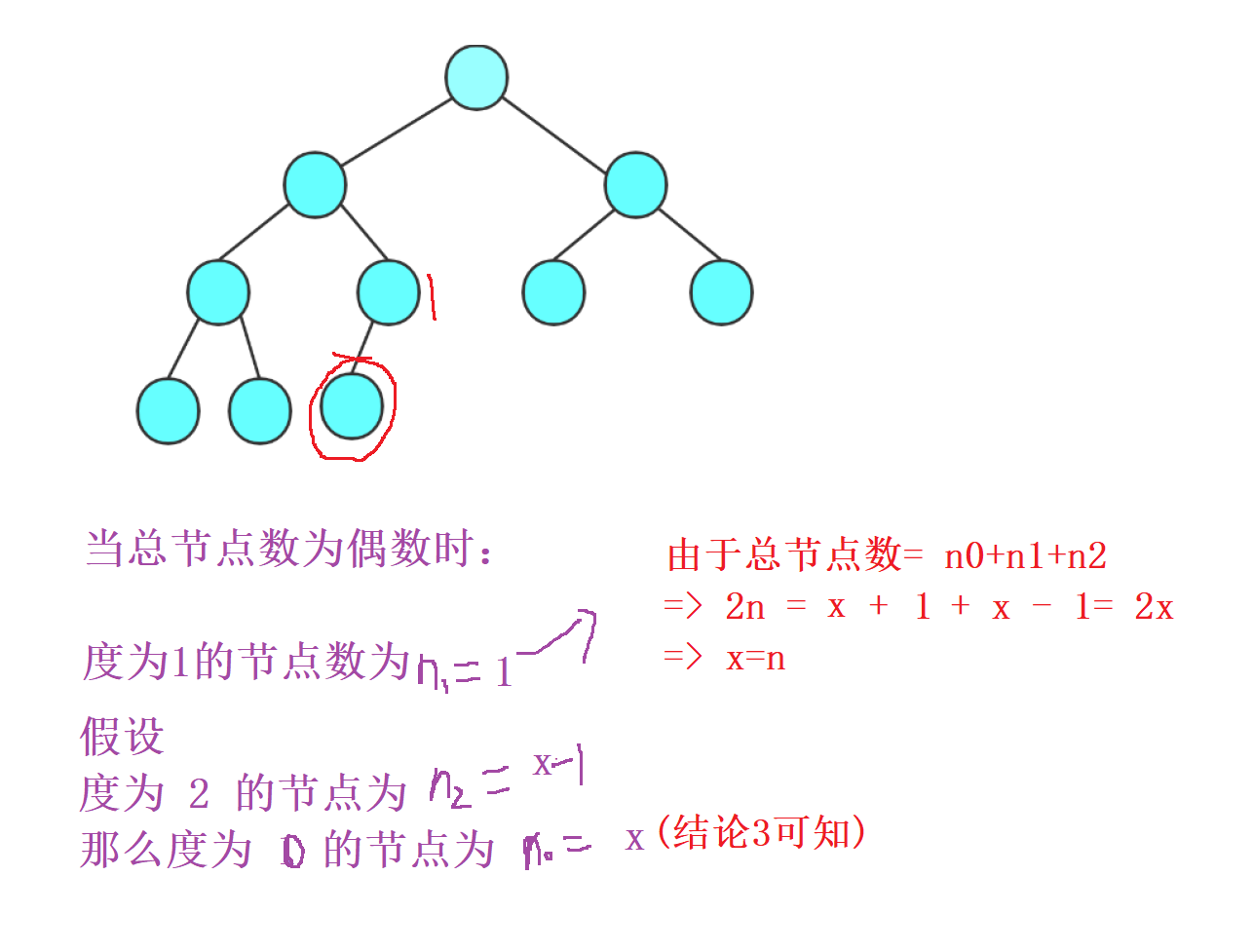
在这里插入图片描述

那么我们就可以通过上面的推导轻松的解读 n = x , 从而选 A

鱼式疯言

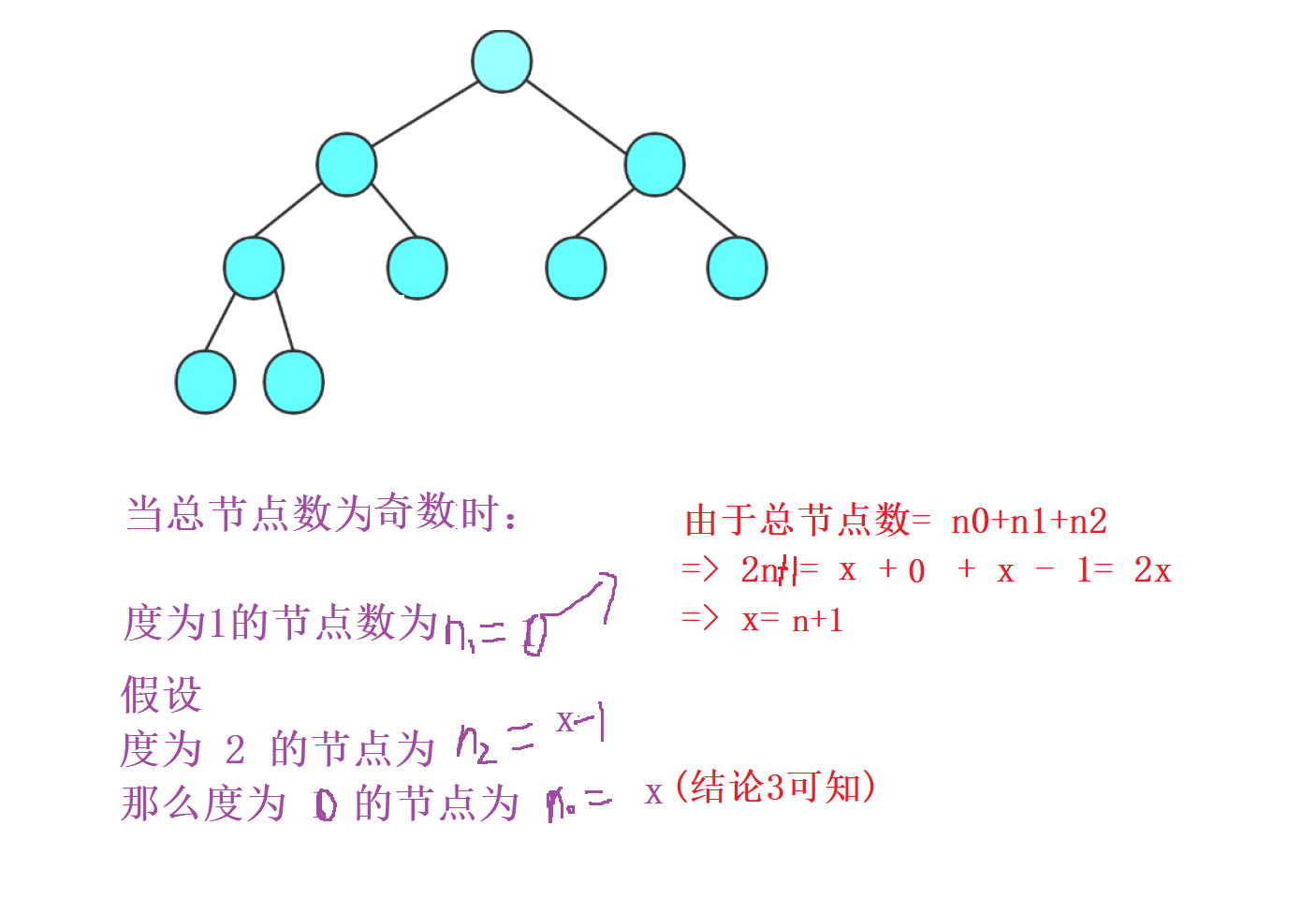
那么有小伙伴问了，如果总节点为 奇数呢 ？ ？ ？

那么我们是不是可以这样推导出

在这里插入图片描述

题目三 :

3.一个具有767个节点的完全二叉树，其叶子节点个数为（）

A. 383
B. 384
C. 385
D. 386

这题的关键信息是 完全二叉树

而且我们还发现这是一颗 总节点为 奇数的完全二叉树 ， 那么我们就可以直接利用我们上面推导出来的结论

那么我们的度为0 的叶子节点的个数就为 ： ==（767+1） / 2 384

故选 B

题目四：

  1. 一颗完全二叉树的节点数为 531 ， 那么这颗树的高度为 （）

A 11
B 10
C 8
D 12

这道题时求树的高度， 也就是最大深度 ， 那么我们就可以直接套用 结论 4 的公式

logf2(531+1) ~= 10 (向上取整)

故： 答案选 B

四. 二叉树的存储

1. 二叉树的存储方式

二叉树的存储结构分为： 顺序存储 和类似于链表的 链式存储。

顺序存储在下一篇文章中会种重点介绍。

二叉树的链式存储是通过 一个一个的节点 引用起来的，常见的表示方式有 =二叉和三叉 表示方式，具体如下：

// 孩子表示法 class Node { int val; // 数据域 Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树 Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树 } // 孩子双亲表示法 class Node { int val; // 数据域 Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树 Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树 Node parent; // 当前节点的根节点 }

孩子双亲表示法 后序在平衡树位置介绍

本文采用 ·孩子表示法· 来构建二叉树。

2. 二叉树的简单创建

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入

为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速 进入二叉树操作学习，

等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

public class BinaryTree{ public static class BTNode{ BTNode left; BTNode right; int value; BTNode(int value){ this.value = value; } } private BTNode root;  public void createBinaryTree(){ BTNode node1 = new BTNode(1); BTNode node1 = new BTNode(2); BTNode node1 = new BTNode(3); BTNode node1 = new BTNode(4); BTNode node1 = new BTNode(5); BTNode node1 = new BTNode(6); root = node1; node1.left = node2; node2.left = node3; node1.right = node4; node4.left = node5; node5.right = node6; } }

注意：上述代码 并不是 创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。

总结

通过本文

我们学习了

  • 树的初识： 树状的结构可以快速的查找和管理， 并明白了树是由递归定义的

  • 二叉树的初识：我们明白了二叉树是度 <= 2 , 可能为 空 也可能有根节点

  • 二叉树的特性以及应用： 深度和节点数的结论特性， 以及最常用的完全二叉树中 度为 2 的节点数 + 1 等于 叶子节点数 ， 和
    最大深度 与 总节点的关系

  • 二叉树的存储 有两种方式： 链式存储和顺序存储，并有孩子表示和孩子双亲表示法的多种类型

如果觉得小编写的还不错的咱可支持 三连 下 (定有回访哦) , 不妥当的咱请评论区 指正

希望我的文章能给各位宝子们带来哪怕一点点的收获就是 小编创作 的最大 动力 💖 💖 💖

在这里插入图片描述

相关阅读
  1. 如何查看和设置我的Android N设备的权限？
  2. 如何在安卓手机上自定义应用图标？
  3. 如何在安卓微信中同时听语音和查看图片？
  4. 华为哪些设备将支持升级至安卓7.0？
  5. 微信安卓软件中Q10功能有哪些独特之处？
  6. 安卓用户如何挑选最佳视频播放器应用？
  7. 安卓系统中用户文件目录的确切位置是什么？
  8. 小米4用户如何安全升级到安卓8.0系统？
  9. 如何成功将魅蓝5升级至安卓原生7.0版本？
  10. 16GB存储的安卓手机是否能满足日常需求？

广告一刻

为您即时展示最新活动产品广告消息，让您随时掌握产品活动新动态！