C++ 改造红黑树,封装map和set
一.前言:已经实现好了的红黑树
set是Key模型的红黑树
map是Key-Value模型的红黑树
我们之前已经把红黑树实现并测试过了
这是Key-Value模型的红黑树
RBTree.h
#pragma once enum Color { RED, BLACK }; template<class K,class V> struct RBTreeNode { RBTreeNode<K,V>* _pLeft; RBTreeNode<K,V>* _pRight; RBTreeNode<K,V>* _pParent; Color _color; pair<K,V> _data; //新插入的节点默认是红色 RBTreeNode(const pair<K,V>& data) :_pLeft(nullptr) ,_pRight(nullptr) ,_pParent(nullptr) ,_color(RED) ,_data(data) {} }; template<class K,class V> class RBTree { typedef RBTreeNode<K,V> Node; public: // 在红黑树中插入值为data的节点,插入成功返回true,否则返回false // 注意:为了简单起见,本次实现红黑树不存储重复性元素 bool Insert(const pair<K,V>& data) { if (_pRoot == nullptr) { _pRoot = new Node(data); //根节点是黑色 _pRoot->_color = BLACK; return true; } Node* cur = _pRoot, * parent = nullptr; while (cur) { //比我小,往左找 if (data.first < cur->_data.first) { parent = cur; cur = cur->_pLeft; } //比我大,往右找 else if (data.first > cur->_data.first) { parent = cur; cur = cur->_pRight; } //有重复元素,插入失败 else { return false; } } //找到空位置,开始插入 cur = new Node(data); //连接父亲和孩子 if (cur->_data.first < parent->_data.first) { parent->_pLeft = cur; } else { parent->_pRight = cur; } cur->_pParent = parent; //父亲是黑色,插入成功 if (parent->_color == BLACK) { return true; } //父亲是红色,需要调整 //且此时爷爷一定是黑色 //根据叔叔的颜色来调整 while (parent && parent->_color == RED) { Node* grandParent = parent->_pParent; //爸爸是爷爷的左孩子 if (parent == grandParent->_pLeft) { Node* uncle = grandParent->_pRight; //根据叔叔的颜色来调整 //1.叔叔存在且为红 if (uncle && uncle->_color == RED) { //修改爸爸,叔叔,爷爷的颜色 uncle->_color = parent->_color = BLACK; grandParent->_color = RED; //此时视爷爷为新插入的红色节点继续向上影响 cur = grandParent; parent = cur->_pParent; } //2.叔叔不存在或者叔叔是黑 else { //1.我是爸爸的左孩子 if (parent->_pLeft == cur) { //对爷爷进行一次右旋 RotateR(grandParent); //把爷爷改成红色,爸爸改成黑色 grandParent->_color = RED; parent->_color = BLACK; //此时爸爸是黑色,无需break,当然break也可以,因此爸爸是黑色,下次循环就不会进入了 } //2.我是爸爸的右孩子 else { //1.对爸爸进行左旋 RotateL(parent); //2.对爷爷右旋 RotateR(grandParent); //3.孩子改成黑色,爷爷改成红色 cur->_color = BLACK; grandParent->_color = RED; //4.一定要break,如果不break的话,因为爸爸是红色,所以循环会继续,此时就乱套了 break; } } } //爸爸是爷爷的右孩子 else { Node* uncle = grandParent->_pLeft; //1.叔叔存在且为红 if (uncle && uncle->_color == RED) { uncle->_color = parent->_color = BLACK; grandParent->_color = RED; cur = grandParent; parent = cur->_pParent; } //2.叔叔不存在或者叔叔为黑 else { //1.我是爸爸的右孩子 if (parent->_pRight == cur) { //对爷爷左旋 RotateL(grandParent); //爷爷改成红色,爸爸改成黑色 grandParent->_color = RED; parent->_color = BLACK; //此时爸爸是黑色,无需break,当然break也可以,因此爸爸是黑色,下次循环就不会进入了 } //2.我是爸爸的左孩子 else { //1.对爸爸右旋 RotateR(parent); //2.对爷爷左旋 RotateL(grandParent); //3.把孩子改成黑色,爷爷改成红色 cur->_color = BLACK; grandParent->_color = RED; //4.一定要break,如果不break的话,因为爸爸是红色,所以循环会继续,此时就乱套了 break; } } } } _pRoot->_color = BLACK; return true; } // 检测红黑树中是否存在关键字为key的节点,存在返回该节点的地址,否则返回nullptr Node* Find(const K& key) { Node* cur = _pRoot; while (cur) { if (cur->_data.first > key) { cur = cur->_pLeft; } else if (cur->_data.second < key) { cur = cur->_pRight; } else { return cur; } } return nullptr; } // 检测红黑树是否为有效的红黑树,注意:其内部主要依靠_IsValidRBTRee函数检测 bool IsValidRBTRee() { //1.空树是红黑树 if (_pRoot == nullptr) { return true; } //2.根节点不能为红色 if (_pRoot->_color == RED) { return false; } //3.为了验证性质: 红黑树的任意一条路径上的黑色节点个数相同 找参考值 size_t ReferenceCount = 0; Node* cur = _pRoot; while (cur) { if (cur->_color == BLACK) { ReferenceCount++; } cur = cur->_pLeft; } return _IsValidRBTRee(_pRoot, 0, ReferenceCount); } void InOrder() { _InOrder(_pRoot); } private: bool _IsValidRBTRee(Node* pRoot, size_t blackCount, size_t& ReferenceCount) { if (pRoot == nullptr) { if (blackCount != ReferenceCount) { cout << "存在黑色节点数量不相等的路径" << endl; return false; } return true; } //验证性质: 红黑树中不能存在连续的红色节点 //如果一个节点是红色,该节点一定不是根节点,因此该节点一定有父亲 //只需要保证红色节点的父亲不是红色节点即可 if (pRoot->_color == RED) { if (pRoot->_pParent->_color == RED) { cout << "存在连续的红色节点" << endl; return false; } } else { blackCount++; } return _IsValidRBTRee(pRoot->_pLeft, blackCount, ReferenceCount) && _IsValidRBTRee(pRoot->_pRight, blackCount, ReferenceCount); } // 右单旋 void RotateR(Node* pParent) { Node* subL = pParent->_pLeft; Node* subLR = subL->_pRight; Node* grandParent = pParent->_pParent; subL->_pRight = pParent; pParent->_pParent = subL; pParent->_pLeft = subLR; if (subLR) subLR->_pParent = pParent; if (grandParent == nullptr) { _pRoot = subL; _pRoot->_pParent = nullptr; } else { if (pParent == grandParent->_pLeft) { grandParent->_pLeft = subL; } else { grandParent->_pRight = subL; } subL->_pParent = grandParent; } } // 左单旋 void RotateL(Node* pParent) { Node* subR = pParent->_pRight; Node* subRL = subR->_pLeft; Node* grandParent = pParent->_pParent; pParent->_pParent = subR; subR->_pLeft = pParent; pParent->_pRight = subRL; if (subRL) subRL->_pParent = pParent; //说明此时pParent是_pRoot if (grandParent == nullptr) { _pRoot = subR; _pRoot->_pParent = nullptr; } //说明此时pParent所在的树是一颗子树,需要跟父亲链接 else { if (pParent == grandParent->_pLeft) { grandParent->_pLeft = subR; } else { grandParent->_pRight = subR; } subR->_pParent = grandParent; } } void _InOrder(Node* root) { if (root == nullptr) return; _InOrder(root->_pLeft); cout << root->_data.first << " " << root->_data.second << " "; _InOrder(root->_pRight); } private: Node* _pRoot = nullptr; }; 要想用红黑树来封装set和map,我们首先想到的是在搞一份Key模型的红黑树,
然后用Key模型红黑树来封装set,Key-Value模型红黑树封装map
但是STL库中set和map的设计却不是这样的
它们都是只用了一份红黑树,怎么做到的呢?
下面就让我们来探索一下
二.简化STL库里面对于map和set的封装
红黑树的源码:是一个KV模型的红黑树
它是通过传入的Value的值来判断类型,利用模板的技术实现的一棵泛型的红黑树
通过模板的实例化,实现了map和set
1.STL库中红黑树的简化代码
我们挑选出一部分很重要的成员来看看STL库中的红黑树是怎么个泛型法呢?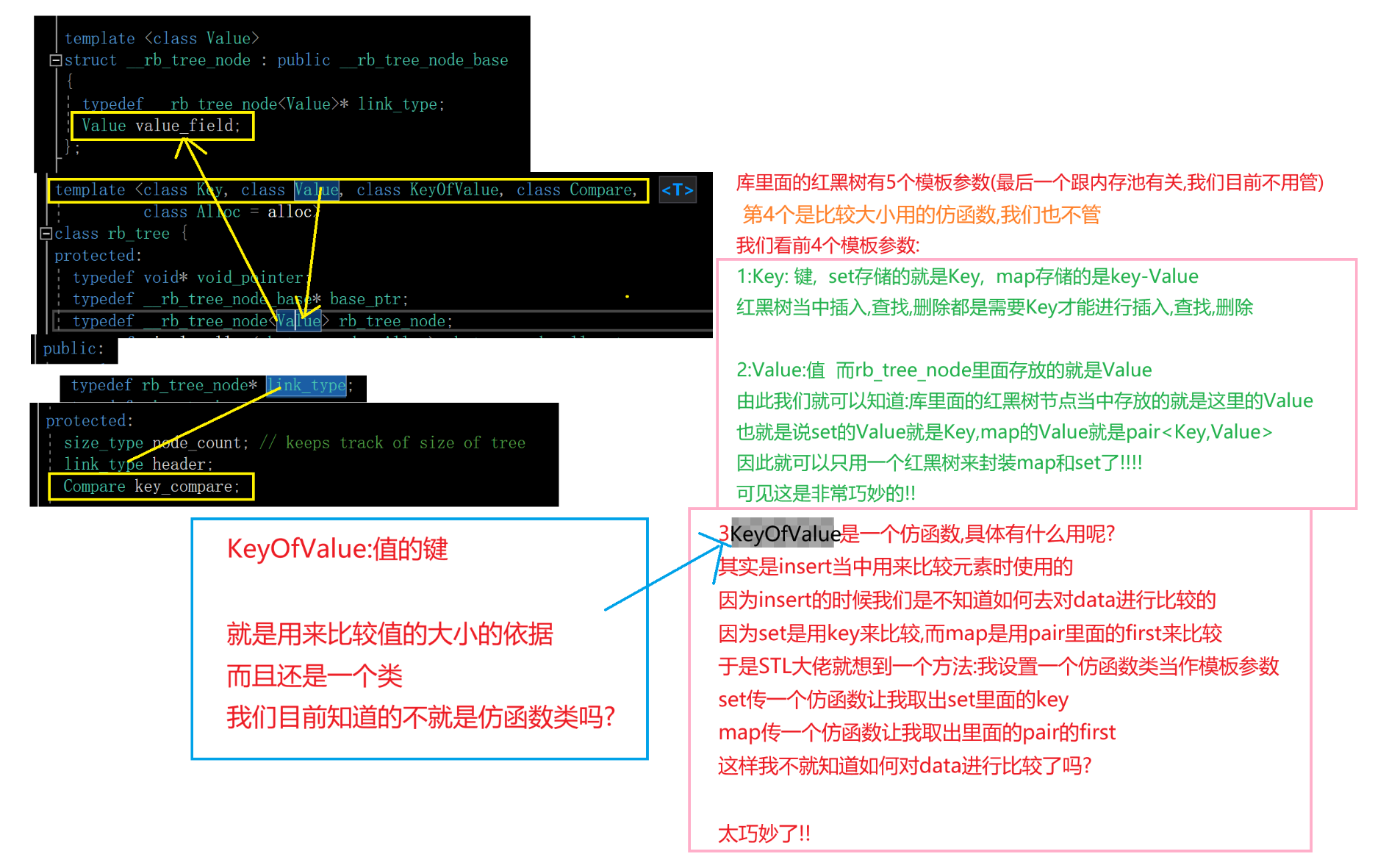
2.STL库中set的简化代码
下面我们看一下set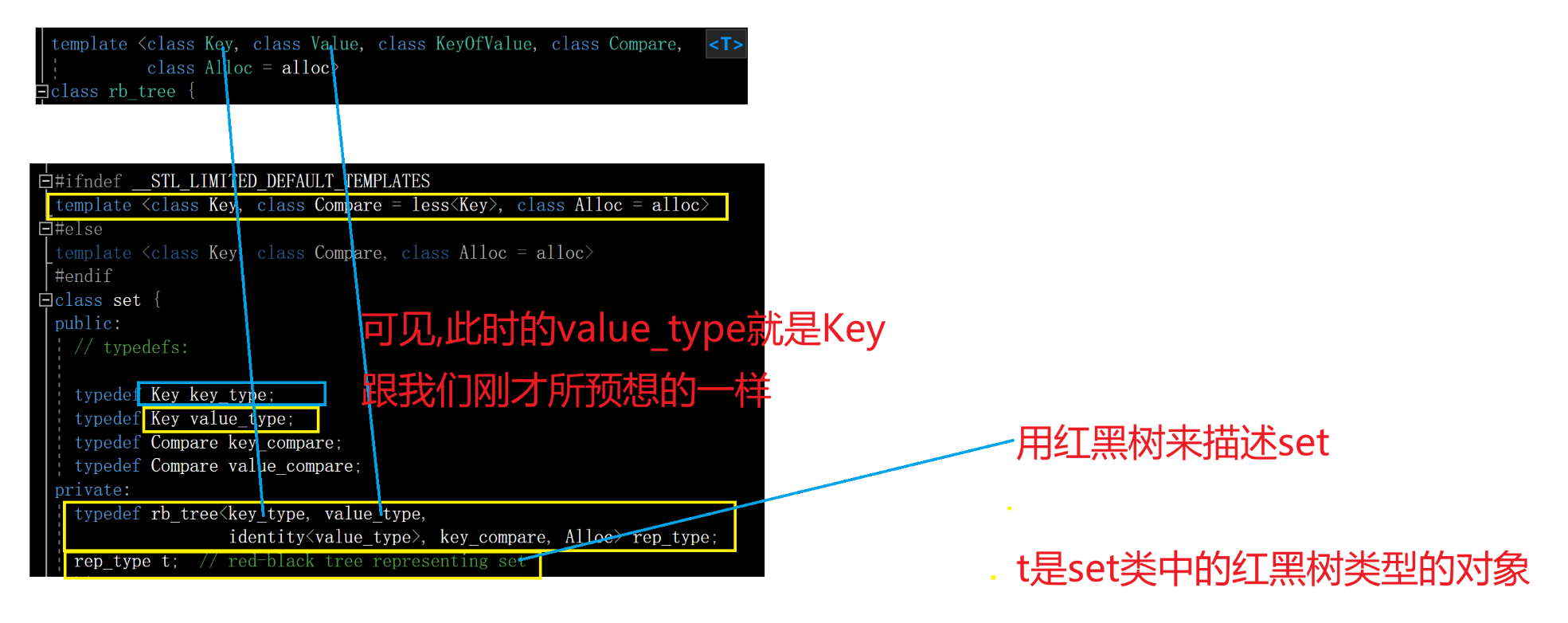
3.STL库中map的简化代码
下面我们看一下map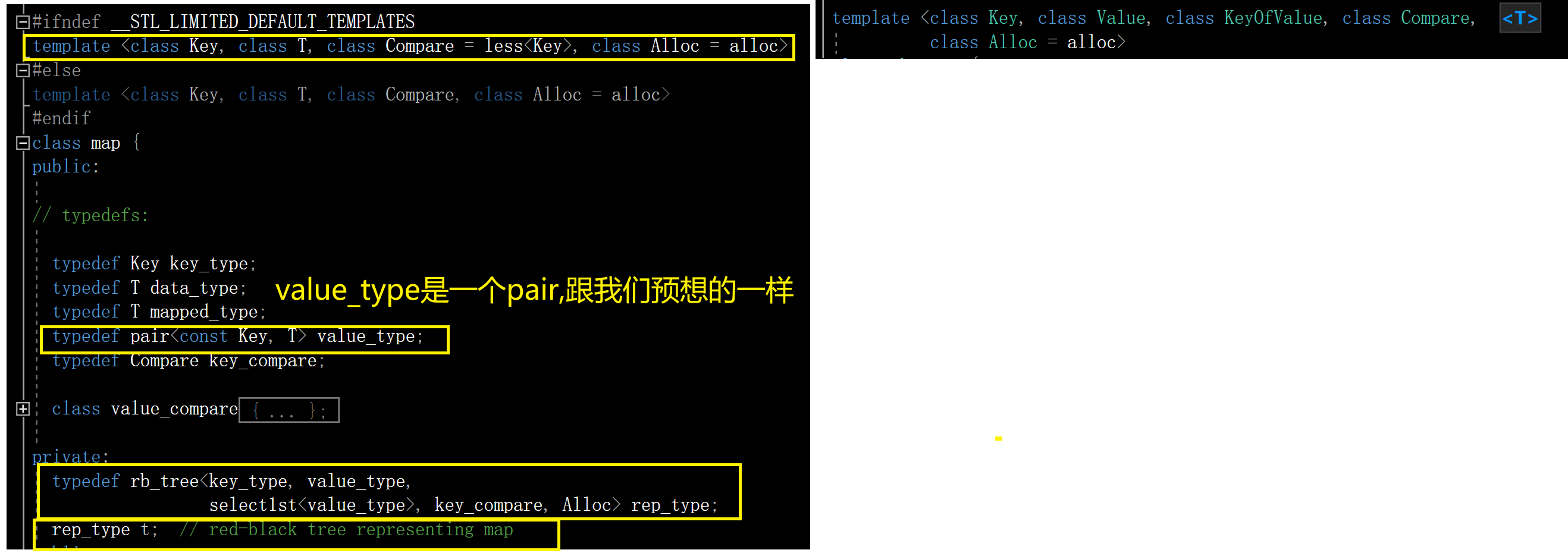
4.封装map和set的第一步

RBTree.h
template<class K, class V> class RBTree 对于V这个模板参数:
可能是键值Key,也可能是由Key和Value共同组成的键值对pair
MySet.h
对于set而言,传入底层红黑树的模板参数就是Key和Key
template<class K> class set { private: RBTree<K, K> _root; }; MyMap.h
对于map而言,传入底层红黑树的模板参数就是Key和pair<const Key,Value>
template<class K, class V> class map { private: //我们知道:map的Key不允许被修改,Value允许被修改 //因此pair里面的K加上const修饰 RBTree<K, pair<const K, V>> _root; }; 5.红黑树第一个模板参数的价值
通过上面的传参,我们可以知道:
只需要对于红黑树的第二个模板参数传入不同的值就可以对set和map进行很好地区分
那么红黑树的第一个模板参数是不是就没有用了呢?
对于insert(const Value& v)来说,是这样的,因为插入的值就是value
set的value是key,map的value是pair
但是对于find(const Key& k)来说,查找的依据是key,对于set是可以的
但是对于map来说,它的value是一个键值对,而我们是需要key来查找的,因此第一个模板参数不能不要
6.红黑树节点的定义

enum Color { RED, BLACK }; template<class T> struct RBTreeNode { RBTreeNode<T>* _pLeft; RBTreeNode<T>* _pRight; RBTreeNode<T>* _pParent; Color _color; T _data; //新插入的节点默认是红色 RBTreeNode(const T& data) :_pLeft(nullptr) , _pRight(nullptr) , _pParent(nullptr) , _color(RED) , _data(data) {} }; 三.仿函数
1.解除仿函数的误解
在学习优先级队列的时候我们遇到了仿函数
当时我们写了一个greater的仿函数,传入greater就能建小堆
传入less就能建大堆
当时我们知道:仿函数是一个类,主要重载operator()
不过仿函数不仅仅可以用于比较大小,这是我们常有的一大误解
2.仿函数在这里的价值
由于红黑树不知道传的是set还是map
因此在insert时进行节点键值的比较时,底层红黑树需要使用仿函数来获取键值key,从而才能进行比较
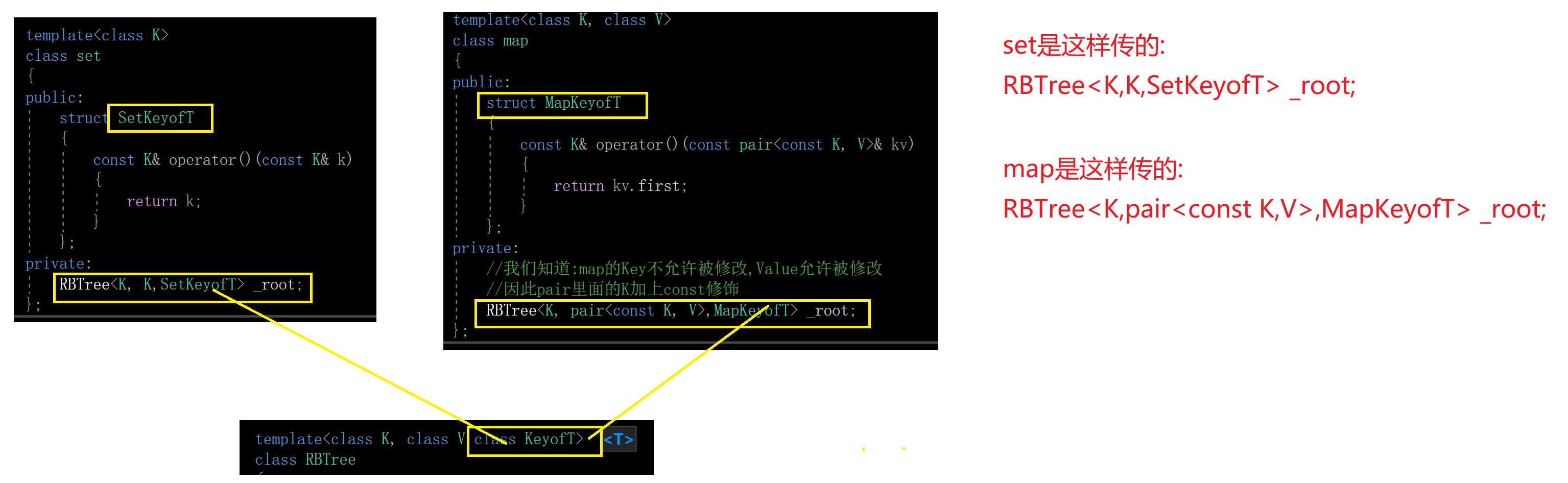
3.set的仿函数
对set而言,仿函数就是返回Key
template<class K> class set { public: struct SetKeyofT { const K& operator()(const K& k) { return k; } }; private: RBTree<K, K,SetKeyofT> _root; }; 4.map的仿函数
对map而言,仿函数就是返回pair的first,也就是Key
template<class K, class V> class map { public: struct MapKeyofT { const K& operator()(const pair<const K, V>& kv) { return kv.first; } }; private: //我们知道:map的Key不允许被修改,Value允许被修改 //因此pair里面的K加上const修饰 RBTree<K, pair<const K, V>,MapKeyofT> _root; }; 5.红黑树的修改
修改之后,因为红黑树的代码太长了,所以这里只列出修改的地方
1.类模板
template<class K, class V,class KeyofT> 2.成员变量
private: Node* _pRoot = nullptr; KeyofT _kot; 3.insert插入时的比较逻辑
//1 参数只需要传V即可(也就是红黑树的第二个模板参数) //对于set而言V就是Key //对于map而言,V就是pair<K,V> bool Insert(const V& data) { if (_pRoot == nullptr) { _pRoot = new Node(data); //根节点是黑色 _pRoot->_color = BLACK; return true; } Node* cur = _pRoot, * parent = nullptr; while (cur) { //比我小,往左找 if (_kot(data) < _kot(cur->_data)) { parent = cur; cur = cur->_pLeft; } //比我大,往右找 else if (_kot(data) > _kot(cur->_data)) { parent = cur; cur = cur->_pRight; } //有重复元素,插入失败 else { return false; } } //找到空位置,开始插入 cur = new Node(data); //连接父亲和孩子 if (_kot(cur->_data) < _kot(parent->_data)) { parent->_pLeft = cur; } //..旋转变色等其他操作,这些操作都无需进行节点的Key有关比较 } 
6.仿函数小总结
四.迭代器
1.迭代器类的定义
跟list类似,红黑树的正向迭代器也是对节点指针进行了一层封装
同样的,为了实现const_iterator,这里传入Ref和Ptr这两个模板参数
不过这里增加了const迭代器和非const迭代器的转化
template<class T, class Ref, class Ptr> struct __TreeIterator { typedef RBTreeNode<T> Node; typedef __TreeIterator<T, T&, T*> iterator; typedef __TreeIterator<T, Ref, Ptr> Self; Node* _node; __TreeIterator(Node* node) :_node(node) {} //普通迭代器和const_iterator的转化 __TreeIterator(const iterator& it) :_node(it._node) {} Ref operator*(); Ptr operator->(); //找中序遍历的下一个节点 Self& operator++(); bool operator!=(const Self& s); bool operator==(const Self& s); }; 2.解引用,!=,==的实现
Ref operator*() { return _node->_data; } Ptr operator->() { return &_node->_data; } bool operator!=(const Self& s) { return _node != s._node; } bool operator==(const Self& s) { return _node == s._node; } 3.operator++
这里的迭代器走的是二叉树的中序遍历,因此++要找到中序遍历的下一个节点
如何找呢?
1.如果节点的右子树不为空,中序的下一个节点就是右子树的最左节点
2.如果节点的右子树为空,那么就需要一直往上找
直到父亲为空或者孩子是父亲的左孩子时,此时的父亲就是中序的下一个节点
//找中序遍历的下一个节点 Self& operator++() { //1.左子树 根节点 右子树 //如果有右孩子,那就是右子树的最左节点 //如果没有右孩子,那往上找直到我是父亲的左孩子或者我的父亲是空节点为止,此时我的父亲就是下一个节点 Node* cur = _node; if (cur->_pRight) { Node* right = cur->_pRight; while (right->_pLeft) { right = right->_pLeft; } _node = right; } else { Node* parent = cur->_pParent; while (parent && parent->_pRight == cur) { cur = parent; parent = cur->_pParent; } _node = parent; } return *this; } 4.给红黑树加上begin和end
begin是中序的第一个节点,也就是最左节点
end是中序的最后一个节点的下一个节点,也就是空节点
跟list一样,普通迭代器就是V V& V*
const_iterator就是V const V& const V*
template<class K, class V,class KeyofT> class RBTree { typedef RBTreeNode<V> Node; public: typedef __TreeIterator<V, V&, V*> iterator; typedef __TreeIterator<V,const V&,const V*> const_iterator; iterator begin() { Node* cur = _pRoot; while (cur && cur->_pLeft) { cur = cur->_pLeft; } return iterator(cur); } iterator end() { return iterator(nullptr); } const_iterator begin() const { Node* cur = _pRoot; while (cur && cur->_pLeft) { cur = cur->_pLeft; } return const_iterator(cur); } const_iterator end() const { return const_iterator(nullptr); } //其他成员.... }; 五.set的实现
1.注意
1.typename
直接复用红黑树的接口即可实现set
注意:
typedef typename RBTree<K, K, SetKeyofT>::const_iterator iterator; typename的作用:因为没有实例化的模板是区分不了静态变量和类型的,因此需要我们使用typename告诉编译器这是类型
2.set的特性
库里面的set是不允许修改里面的值的
也就是说set的普通迭代器和const迭代器其实都是const迭代器
因此都复用红黑树的const_iterator即可
2.set的代码
namespace wzs { template<class K> class set { public: struct SetKeyofT { const K& operator()(const K& k) { return k; } }; typedef typename RBTree<K, K, SetKeyofT>::const_iterator iterator; typedef typename RBTree<K, K, SetKeyofT>::const_iterator const_iterator; iterator begin() const { return _root.begin(); } iterator end() const { return _root.end(); } pair<iterator, bool> insert(const K& k) { return _root.Insert(k); } private: RBTree<K, K, SetKeyofT> _root; }; } 六.map的实现
1.operator[]的说明
STL库里面的map容器的方括号[]的作用:
返回值: 插入成功:pair<新插入的key所在的节点的iterator,true> 插入失败:pair<已经存在的key所在的节点的iterator,false> 作用: 如果插入成功,那么operator[]相当于insert 如果插入失败,那么operator[]相当于find 也就是说operator[]有多重技能 operator[]是map的一个非常重要的函数,可以实现3个功能:插入,查找,修改 这是对源码的一个简化:
operator[]:给一个key,返回这个key所对应的value的引用 简化前: mapped_type& operator[](const Key_type& k) { return (*(this->insert(make_pair(k,mapped_type())))).first).second; } 简化后 V& operator(const K& key) { pair<iterator,bool> ret=insert(key,V());//V():value的默认构造的匿名对象 return ret.first->second; 2.map的代码
namespace wzs { template<class K, class V> class map { public: struct MapKeyofT { const K& operator()(const pair<const K, V>& kv) { return kv.first; } }; typedef typename RBTree<K, pair<const K, V>, MapKeyofT>::iterator iterator; typedef typename RBTree<K, pair<const K, V>, MapKeyofT>::const_iterator const_iterator; iterator begin() { return _root.begin(); } iterator end() { return _root.end(); } const_iterator begin() const { return _root.begin(); } const_iterator end() const { return _root.end(); } pair<iterator, bool> insert(const pair<const K, V>& kv) { return _root.Insert(kv); } /* operator[]:给一个key,返回这个key所对应的value的引用 简化前: mapped_type& operator[](const Key_type& k) { return (*(this->insert(make_pair(k,mapped_type())))).first).second; } 简化后 V& operator(const K& key) { pair<iterator,bool> ret=insert(key,V());//V():value的默认构造的匿名对象 return ret.first->second; } */ V& operator[](const K& k) { pair<iterator, bool> ret = insert(make_pair(k, V())); return ret.first->second; } private: //我们知道:map的Key不允许被修改,Value允许被修改 //因此pair里面的K加上const修饰 RBTree<K, pair<const K, V>, MapKeyofT> _root; }; } 七.改造后的红黑树代码
#pragma once namespace wzs { enum Color { RED, BLACK }; template<class T> struct RBTreeNode { RBTreeNode<T>* _pLeft; RBTreeNode<T>* _pRight; RBTreeNode<T>* _pParent; Color _color; T _data; //新插入的节点默认是红色 RBTreeNode(const T& data) :_pLeft(nullptr) , _pRight(nullptr) , _pParent(nullptr) , _color(RED) , _data(data) {} }; //给红黑树增加迭代器 template<class T, class Ref, class Ptr> struct __TreeIterator { typedef RBTreeNode<T> Node; typedef __TreeIterator<T, T&, T*> iterator; typedef __TreeIterator<T, Ref, Ptr> Self; Node* _node; __TreeIterator(Node* node) :_node(node) {} //const迭代器和普通迭代器的转化 __TreeIterator(const iterator& it) :_node(it._node) {} Ref operator*() { return _node->_data; } Ptr operator->() { return &_node->_data; } //找中序遍历的下一个节点 Self& operator++() { //1.左子树 根节点 右子树 //如果有右孩子,那就是右子树的最左节点 //如果没有右孩子,那往上找直到我是父亲的左孩子或者我的父亲是空节点为止,此时我的父亲就是下一个节点 Node* cur = _node; if (cur->_pRight) { Node* right = cur->_pRight; while (right->_pLeft) { right = right->_pLeft; } _node = right; } else { Node* parent = cur->_pParent; while (parent && parent->_pRight == cur) { cur = parent; parent = cur->_pParent; } _node = parent; } return *this; } bool operator!=(const Self& s) { return _node != s._node; } bool operator==(const Self& s) { return _node == s._node; } }; template<class K, class V,class KeyofT> class RBTree { typedef RBTreeNode<V> Node; public: typedef __TreeIterator<V, V&, V*> iterator; typedef __TreeIterator<V, const V&, const V*> const_iterator; iterator begin() { Node* cur = _pRoot; while (cur && cur->_pLeft) { cur = cur->_pLeft; } return iterator(cur); } iterator end() { return iterator(nullptr); } const_iterator begin() const { Node* cur = _pRoot; while (cur && cur->_pLeft) { cur = cur->_pLeft; } return const_iterator(cur); } const_iterator end() const { return const_iterator(nullptr); } //1,参数只需要传V即可(也就是红黑树的第二个模板参数) //对于set而言V就是Key //对于map而言,V就是pair<K,V> pair<iterator, bool> Insert(const V& data) { if (_pRoot == nullptr) { _pRoot = new Node(data); //根节点是黑色 _pRoot->_color = BLACK; return make_pair(iterator(_pRoot), true); } Node* cur = _pRoot, * parent = nullptr; while (cur) { //比我小,往左找 if (_kot(data) < _kot(cur->_data)) { parent = cur; cur = cur->_pLeft; } //比我大,往右找 else if (_kot(data) > _kot(cur->_data)) { parent = cur; cur = cur->_pRight; } //有重复元素,插入失败 else { return make_pair(iterator(cur), false); } } //找到空位置,开始插入 cur = new Node(data); Node* newnode = cur; //连接父亲和孩子 if (_kot(cur->_data) < _kot(parent->_data)) { parent->_pLeft = cur; } else { parent->_pRight = cur; } cur->_pParent = parent; //父亲是黑色,插入成功 if (parent->_color == BLACK) { return make_pair(iterator(newnode), true); } //父亲是红色,需要调整 //且此时爷爷一定是黑色 //根据叔叔的颜色来调整 while (parent && parent->_color == RED) { Node* grandParent = parent->_pParent; //爸爸是爷爷的左孩子 if (parent == grandParent->_pLeft) { Node* uncle = grandParent->_pRight; //根据叔叔的颜色来调整 //1.叔叔存在且为红 if (uncle && uncle->_color == RED) { //修改爸爸,叔叔,爷爷的颜色 uncle->_color = parent->_color = BLACK; grandParent->_color = RED; //此时视爷爷为新插入的红色节点继续向上影响 cur = grandParent; parent = cur->_pParent; } //2.叔叔不存在或者叔叔是黑 else { //1.我是爸爸的左孩子 if (parent->_pLeft == cur) { //对爷爷进行一次右旋 RotateR(grandParent); //把爷爷改成红色,爸爸改成黑色 grandParent->_color = RED; parent->_color = BLACK; //此时爸爸是黑色,无需break,当然break也可以,因此爸爸是黑色,下次循环就不会进入了 } //2.我是爸爸的右孩子 else { //1.对爸爸进行左旋 RotateL(parent); //2.对爷爷右旋 RotateR(grandParent); //3.孩子改成黑色,爷爷改成红色 cur->_color = BLACK; grandParent->_color = RED; //4.一定要break,如果不break的话,因为爸爸是红色,所以循环会继续,此时就乱套了 break; } } } //爸爸是爷爷的右孩子 else { Node* uncle = grandParent->_pLeft; //1.叔叔存在且为红 if (uncle && uncle->_color == RED) { uncle->_color = parent->_color = BLACK; grandParent->_color = RED; cur = grandParent; parent = cur->_pParent; } //2.叔叔不存在或者叔叔为黑 else { //1.我是爸爸的右孩子 if (parent->_pRight == cur) { //对爷爷左旋 RotateL(grandParent); //爷爷改成红色,爸爸改成黑色 grandParent->_color = RED; parent->_color = BLACK; //此时爸爸是黑色,无需break,当然break也可以,因此爸爸是黑色,下次循环就不会进入了 } //2.我是爸爸的左孩子 else { //1.对爸爸右旋 RotateR(parent); //2.对爷爷左旋 RotateL(grandParent); //3.把孩子改成黑色,爷爷改成红色 cur->_color = BLACK; grandParent->_color = RED; //4.一定要break,如果不break的话,因为爸爸是红色,所以循环会继续,此时就乱套了 break; } } } } _pRoot->_color = BLACK; return make_pair(iterator(newnode), true); } // 检测红黑树中是否存在关键字为key的节点,存在返回该节点的地址,否则返回nullptr Node* Find(const K& key) { Node* cur = _pRoot; while (cur) { if (cur->_data.first > key) { cur = cur->_pLeft; } else if (cur->_data.second < key) { cur = cur->_pRight; } else { return cur; } } return nullptr; } // 检测红黑树是否为有效的红黑树,注意:其内部主要依靠_IsValidRBTRee函数检测 bool IsValidRBTRee() { //1.空树是红黑树 if (_pRoot == nullptr) { return true; } //2.根节点不能为红色 if (_pRoot->_color == RED) { return false; } //3.为了验证性质: 红黑树的任意一条路径上的黑色节点个数相同 找参考值 size_t ReferenceCount = 0; Node* cur = _pRoot; while (cur) { if (cur->_color == BLACK) { ReferenceCount++; } cur = cur->_pLeft; } return _IsValidRBTRee(_pRoot, 0, ReferenceCount); } void InOrder() { _InOrder(_pRoot); } private: bool _IsValidRBTRee(Node* pRoot, size_t blackCount, size_t& ReferenceCount) { if (pRoot == nullptr) { if (blackCount != ReferenceCount) { cout << "存在黑色节点数量不相等的路径" << endl; return false; } return true; } //验证性质: 红黑树中不能存在连续的红色节点 //如果一个节点是红色,该节点一定不是根节点,因此该节点一定有父亲 //只需要保证红色节点的父亲不是红色节点即可 if (pRoot->_color == RED) { if (pRoot->_pParent->_color == RED) { cout << "存在连续的红色节点" << endl; return false; } } else { blackCount++; } return _IsValidRBTRee(pRoot->_pLeft, blackCount, ReferenceCount) && _IsValidRBTRee(pRoot->_pRight, blackCount, ReferenceCount); } // 右单旋 void RotateR(Node* pParent) { Node* subL = pParent->_pLeft; Node* subLR = subL->_pRight; Node* grandParent = pParent->_pParent; subL->_pRight = pParent; pParent->_pParent = subL; pParent->_pLeft = subLR; if (subLR) subLR->_pParent = pParent; if (grandParent == nullptr) { _pRoot = subL; _pRoot->_pParent = nullptr; } else { if (pParent == grandParent->_pLeft) { grandParent->_pLeft = subL; } else { grandParent->_pRight = subL; } subL->_pParent = grandParent; } } // 左单旋 void RotateL(Node* pParent) { Node* subR = pParent->_pRight; Node* subRL = subR->_pLeft; Node* grandParent = pParent->_pParent; pParent->_pParent = subR; subR->_pLeft = pParent; pParent->_pRight = subRL; if (subRL) subRL->_pParent = pParent; //说明此时pParent是_pRoot if (grandParent == nullptr) { _pRoot = subR; _pRoot->_pParent = nullptr; } //说明此时pParent所在的树是一颗子树,需要跟父亲链接 else { if (pParent == grandParent->_pLeft) { grandParent->_pLeft = subR; } else { grandParent->_pRight = subR; } subR->_pParent = grandParent; } } void _InOrder(Node* root) { if (root == nullptr) return; _InOrder(root->_pLeft); cout << root->_data.first << " " << root->_data.second << " "; _InOrder(root->_pRight); } private: Node* _pRoot = nullptr; KeyofT _kot; }; } 测试代码:
#include <iostream> using namespace std; #include <vector> #include "MySet.h" #include "MyMap.h" namespace wzs { void test1() { map<int, int> m; m.insert(make_pair(1, 1)); m.insert(make_pair(2, 1)); m.insert(make_pair(3, 1323)); m.insert(make_pair(4, 111)); m.insert(make_pair(3, 12)); m.insert(make_pair(1, 1)); map<int, int>::iterator it = m.begin(); while(it != m.end()) { it->second = 10; cout << it->first << " : " << it->second << endl; ++it; } cout << endl; map<int, int>::const_iterator cit = m.begin(); while (cit != m.end()) { //it->first = 10; //cit->second = 10; cout << cit->first << " : " << cit->second << endl; ++cit; } } void test2() { set<int> s; s.insert(1); s.insert(2); s.insert(3); s.insert(4); set<int>::iterator it = s.begin(); while (it != s.end()) { //*it += 1; cout << *it << " "; ++it; } cout << endl; set<int>::const_iterator cit = s.begin(); while (cit != s.end()) { //*cit += 1; cout << *cit << " "; ++cit; } cout << endl; } void test3() { //统计次数 map<string, int> countMap; vector<string> dict = { "hello","hi","who","hi","hi","who","which" }; for (auto& e : dict) { countMap[e]++; } for (auto& e : countMap) { cout << e.first << ":" << e.second << endl; } } } int main() { wzs::test1(); cout << endl; wzs::test2(); cout << endl; wzs::test3(); return 0; } 
以上就是C++ 改造红黑树,封装map和set的全部内容,希望能对大家有所帮助!
