Hi~!这里是奋斗的小羊,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~
💥💥个人主页:奋斗的小羊
💥💥所属专栏:C语言
🚀本系列文章为个人学习笔记,在这里撰写成文一为巩固知识,二为展示我的学习过程及理解。文笔、排版拙劣,望见谅。
目录

前言
栈作为一种比较特殊的存储结构,可以使用数组、单链表、双向链表等多种方法来实现,其在函数调用和递归、表达式求值、浏览器的历史记录、撤销操作、系统调用等多个场景中被广泛使用。
一、栈
1、栈的结构和概念
栈是一种特殊的线性表,其只允许在固定的一端进行插入和删除元素的操作。
进行元素的插入和删除的一端称为栈顶,另一端称为栈底,栈中的数据遵循后进先出的原则。
压栈:栈的插入操作叫做进栈、压栈、入栈
出栈:栈的删除操作叫做出栈
栈的结构类似于桶,只能从上面进,只能从上面出,因此我们一般只关心栈顶。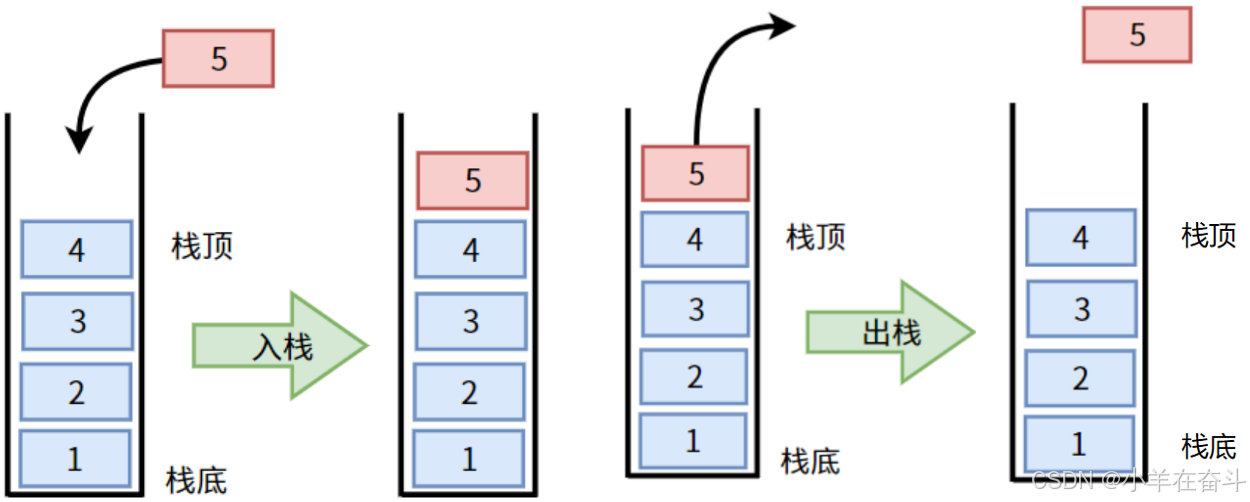
2、实现栈的方法选择
了解的栈的结构,接下来就要考虑如何实现栈。
在这之前我们学习了顺序表(底层就是数组)和链表,链表又分单链表和双向链表,用哪个方法实现效果最好呢?
上篇文章中我们简单地列举的顺序表和链表的比较,如下:
| 顺序表 | 链表(双向链表) | |
|---|---|---|
| 存储空间上 | 逻辑、物理上都连续 | 逻辑上连续、物理上不一定连续 |
| 随机访问 | 复杂度O(1) | 复杂度O(N) |
| 任意位置插入或删除数据 | 需要挪动数据,复杂度O(N) | 只需要改变指针指向 |
| 插入 | 动态顺序表,空间不够时扩容,扩容本身就有消耗,还容易空间浪费 | 没有容量的概念 |
| 应用场景 | 数据高效存储+频繁访问 | 任意位置频繁插入、删除数据 |
| 缓存利用率 | 高 | 低 |
其中我们关键看缓存利用率,简单地说缓存利用率是指计算机系统中缓存(如CPU缓存、内存缓存等)被有效利用的程度。
CPU执行指令运算要访问数据,会先去缓存中找有没有这个数据,如果有,说明缓存命中了;如果没有,说明缓存未命中,就从主存中读取一段连续内存空间的数据到缓存,继续找。
而我们知道在物理结构上顺序表是连续的,链表不连续。那从主存中读取一段连续内存空间的数据到缓存时链表读取到的很可能不是我们想要的数据,从而造成缓存污染。
虽然顺序表在扩容的时候时间和空间都有消耗,而且还容易存在空间浪费,但是动态扩容也不是说很频繁,只有在空间不够时才扩容。
其实在实现栈上顺序表和链表只是五十步和百步的区别,只是相对而言顺序表更好一点。
3、栈的实现
3.1完整代码
用顺序表的方法实现栈,和我们之前实现的顺序表没多大区别,只是栈中的元素只能从栈顶进从栈顶出,遵循后进先出的原则。
这里我们就先展示用顺序表的方法实现的栈的完整代码,其中的细节再一一介绍。stack.h:
#pragma once #include <stdio.h> #include <stdlib.h> #include <assert.h> #include <stdbool.h> typedef int st_data_type; typedef struct stack { st_data_type* arr; int top; int capacity; }stack; //初始化和销毁 void stack_init(stack* pst); void stack_destroy(stack* pst); //入栈和出栈 void stack_push(stack* pst, st_data_type x); void stack_pop(stack* pst); //取出栈顶元素 st_data_type stack_top(stack* pst); //判空 bool stack_empty(stack* pst); //获取数据个数 int stack_size(stack* pst); stack.c:
#include "stack.h" //初始化 void stack_init(stack* pst) { assert(pst); pst->arr = NULL; pst->top = pst->capacity = 0; } //入栈 void stack_push(stack* pst, st_data_type x) { assert(pst); if (pst->capacity == pst->top) { int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity; st_data_type* tmp = (st_data_type*)realloc(pst->arr, newcapacity * sizeof(st_data_type)); if (tmp == NULL) { perror("realloc fail!"); return 1; } pst->arr = tmp; tmp = NULL; pst->capacity = newcapacity; } pst->arr[pst->top] = x; pst->top++; } //出栈 void stack_pop(stack* pst) { assert(pst); assert(pst->top > 0); pst->top--; } //取出栈顶元素 st_data_type stack_top(stack* pst) { assert(pst); assert(pst->top > 0); return pst->arr[pst->top-1]; } //销毁 void stack_destroy(stack* pst) { assert(pst); free(pst->arr); pst->arr = NULL; pst->capacity = pst->top = 0; } //判空 bool stack_empty(stack* pst) { assert(pst); return pst->top == 0; } //获取元素个数 int stack_size(stack* pst) { assert(pst); return pst->top; } test.c:
#define _CRT_SECURE_NO_WARNINGS #include "stack.h" void test() { stack st; stack_init(&st); //... stack_push(&st, 1); stack_push(&st, 2); stack_push(&st, 3); stack_push(&st, 4); stack_destroy(&st); } int main() { test(); return 0; } 可以看到因为栈结构的特殊,栈的实现比之前的顺序表简单多了,少了很多接口(函数)。
其中初始化、入栈、销毁函数跟之前实现的顺序表是一样的,这里就不再赘述。
3.2特殊的接口
出栈:
//出栈 void stack_pop(stack* pst) { assert(pst); assert(pst->top > 0); pst->top--; } 因为出栈就是删除栈顶的一个元素数据,所以出栈的实现只需要将top--就行了。
取出栈顶元素数据:
//取出栈顶元素 st_data_type stack_top(stack* pst) { assert(pst); assert(pst->top > 0); return pst->arr[pst->top-1]; } 在取栈顶元素的时候,极其容易写出:return pst->arr[pst->top]; 这条代码,因为我们下意识思维会认为最后一个元素数据的下标为top,其实不是的,这里跟顺序表中的size一样表示的是栈中元素的个数,所以栈中最后一个元素的下标是top-1。
判空、获取数据个数:
//判空 bool stack_empty(stack* pst) { assert(pst); return pst->top == 0; } //获取元素个数 int stack_size(stack* pst) { assert(pst); return pst->top; } 如果栈中没有数据,则pst->top == 0;为真,返回ture,反之则返回false。
3.3访问栈的所有元素
由于栈后进先出的特殊结构,访问栈的所有元素我们不能像顺序表那样利用下标循环打印,应该使用下面这种方式:
while (!stack_empty(&pst)) { printf("%d ", stack_top(&pst)); stack_pop(&pst); } 拿到栈顶的元素后再拿下一个元素前需要先将栈顶的元素弹出(也就是删除),才能访问到下一个元素。
但是这也导致了一个问题,就是我们访问完栈中的所有元素后栈也就空了,不过不用担心这是正常现象。
这里有个问题: 栈的原则是后进先出,如果我们入栈的顺序是1、2、3、4,那出栈的顺序一定是4、3、2、1吗?
其实不是的,因为我们可以边进边出。
#define _CRT_SECURE_NO_WARNINGS #include "stack.h" void test() { stack st; stack_init(&st); stack_push(&st, 1); printf("%d ", stack_top(&st)); stack_pop(&st); stack_push(&st, 2); printf("%d ", stack_top(&st)); stack_pop(&st); stack_push(&st, 3); stack_push(&st, 4); while (!stack_empty(&st)) { printf("%d ", stack_top(&st)); stack_pop(&st); } stack_destroy(&st); } int main() { test(); return 0; } 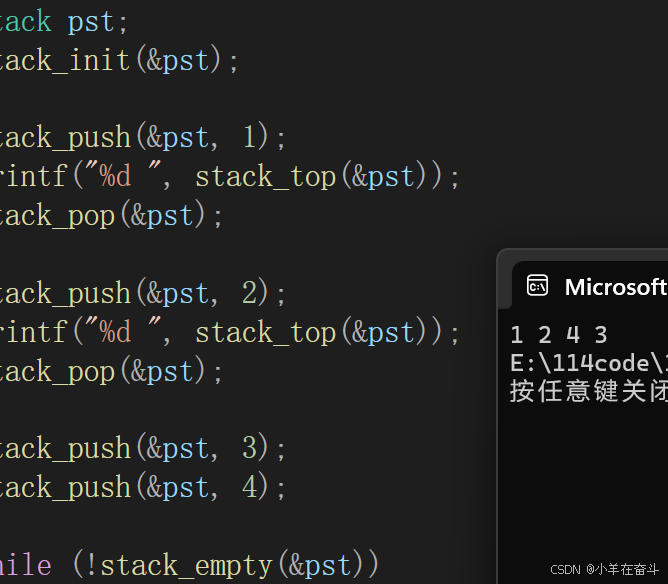
也就是说,出栈的顺序可以有多种。
4、用栈解决括号匹配的问题
题目描述:

我们怎么使用栈的特点来解决这个问题呢?
解题思路:
返回false的情况有两种,一种是数量不匹配,一种是顺序不匹配。
栈有后进先出的特点,而括号匹配的问题首先需要找到若干个左括号,然后再找右括号进行一一配对,如果全部配对成功则返回true,否则返回false。
也就是说当我们拿到字符串中的第一个字符,如果是左括号则压栈,如果是右括号则出栈与右括号配对,只要有一次配对不上就返回false。
有几个需要注意的点或特殊情况:
- 如果拿到的第一个字符就是右括号(也就是栈为空时),这时则直接返回
false- 当在字符串中取到
‘\0’退出循环后,还要再判断一下栈是否为空,因为有可能栈内还剩有压进去的左括号在每次返回前都要先销毁栈,避免内存泄漏
解题过程如下:
bool isValid(char* s) { //创建栈并初始化 stack st; stack_init(&st); while (*s != '\0') { //左括号则压栈 if (*s == '(' || *s == '[' || *s == '{') { stack_push(&st, *s); } //右括号则出栈,配对 else { if (stack_empty(&st))//拿到的第一个字符就是右括号 { stack_destroy(&st); return false; } //取 char top = stack_top(&st); //删 stack_pop(&st); //如果不配对则直接返回false if (top == '(' && *s != ')' || top == '[' && *s != ']' || top == '{' && *s != '}') { stack_destroy(&st);//避免内存泄漏 return false; } } s++; } //判断栈内是否还有未配对的左括号 bool ret = stack_empty(&st); stack_destroy(&st); return ret; } 不管是栈后进先出的原则,还是栈元素访问后就消失的特点,在这个题中都能较好的体现出来。
二、队列
1、队列的概念和结构
队列: 遵循先进先出的原则,即最先被加入队列的元素最先被取出。
入队操作将新元素加入到队列的末尾(队尾),出队操作则移除并返回队列的第一个元素(队头)。
与栈不同的是,队列结构不管怎样,入队和出队的顺序总是一样的。
队列通常应用于解耦和异步通信、任务调度、请求排队、资源分配、数据处理流水线、HTTP请求等多种场景。
栈和队列比较: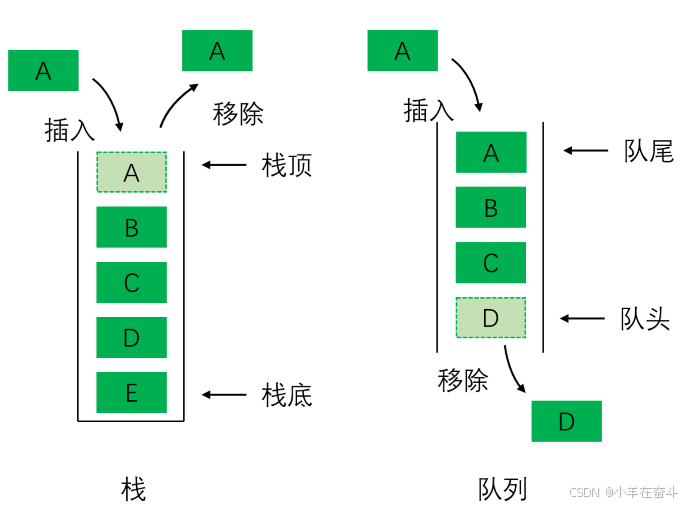
队列既可以用链表实现也可以用数组实现,但单链表结构总体更优一些。因为如果使用数组实现,则出队列时剩余所有数据都要挪动位置,复杂度O(N);
而使用链表实现的队列在插入和删除操作上更高效,不涉及元素搬移的操作。
2、队列的实现
将队列看作一个特殊的单链表,则此单链表只有头删和尾插等操作,如果按照之前单链表的实现来完成队列的尾插,只有一个头节点的地址让尾插效率不是很高,因为还要遍历链表来找尾节点。
所以这里不再使用创建一个结构体指针变量记录第一个节点的方法,我们直接使用两个指针分别记录第一个节点和最后一个节点,这样入队(尾插)和出队(头删)效率更高。
typedef int QDataType; //队列节点结构 typedef struct QueueNode { QDataType data; struct QueueNode* next; }QNode; //队尾插入 void QNodePush(QNode** pphead, QNode** pptail, QDataType x); //队头删除 void QNodePop(QNode** pphead, QNode** pptail); 但是这样既要传两个指针还要传二级指针,为了简化代码我们用结构体变量分装起来,并且再添加一个整型值来记录队列元素个数。
//队列结构 typedef struct Queue { QNode* phead; QNode* ptail; int size; }Que; //初始化队列结构 void QueueInit(Que* pq); //队尾插入 void QNodePush(Que* pq, QDataType x); //队头删除 void QNodePop(Que* pq); //队列元素个数 int QNodeSize(Que* pq); //取队头 QDataType QNodeFront(Que* pq); //取队尾 QDataType QNodeBack(Que* pq); //判空 bool QNodeEmpty(Que* pq); //销毁队列 void QNodeDestroy(Que* pq); 这样一来我们只需要传递结构体指针,就能改变头指针和尾指针的指向,但是这个结构体开始需要初始化一下:
//初始化队列结构 void QueueInit(Que* pq) { assert(pq); pq->phead = pq->ptail = NULL; pq->size = 0; } 队尾插入:
//队尾插入 void QNodePush(Que* pq, QDataType x) { assert(pq); QNode* newnode = (QNode*)malloc(sizeof(QNode)); if (newnode == NULL) { perror("malloc fail"); return; } newnode->data = x; newnode->next = NULL; //没有节点 if (pq->phead == NULL) { pq->phead = pq->ptail = newnode; } else//有节点 { pq->ptail->next = newnode; pq->ptail = newnode; } pq->size++; } 入队(尾插)需要注意的是,如果当前队列没有节点,则头指针和尾指针都要指向新节点。
队头删除:
//队头删除 void QNodePop(Que* pq) { assert(pq); assert(pq->phead);//没有节点 //一个节点 if (pq->phead == pq->ptail) { free(pq->phead); pq->phead = pq->ptail = NULL; } //多个节点 else { QNode* next = pq->phead->next; free(pq->phead); pq->phead = next; } pq->size--; } 出队(头删)分为三种情况,没有节点、一个节点和多个节点。
如果只有一个节点(头指针和尾指针指向同一节点),则在释放掉这个节点后头指针和尾指针都要置NULL。
取队头、取队尾:
//取队头 QDataType QNodeFront(Que* pq) { assert(pq); assert(pq->phead); return pq->phead->data; } //取队尾 QDataType QNodeBack(Que* pq) { assert(pq); assert(pq->ptail); return pq->ptail->data; } while (!QNodeEmpty(&q)) { printf("%d ", QNodeFront(&q)); //元素取完要删除 QNodePop(&q); } 取出队列中的元素后需要弹出此元素才能取到下一个元素,这点与栈相同。
3、队列完整代码
queue.h:
#pragma once #include <stdio.h> #include <stdlib.h> #include <assert.h> #include <stdbool.h> typedef int QDataType; //队列节点结构 typedef struct QueueNode { QDataType data; struct QueueNode* next; }QNode; //队列结构 typedef struct Queue { QNode* phead; QNode* ptail; int size; }Que; //初始化队列结构 void QueueInit(Que* pq); //队尾插入 void QNodePush(Que* pq, QDataType x); //队头删除 void QNodePop(Que* pq); //队列元素个数 int QNodeSize(Que* pq); //取队头 QDataType QNodeFront(Que* pq); //取队尾 QDataType QNodeBack(Que* pq); //判空 bool QNodeEmpty(Que* pq); //销毁队列 void QNodeDestroy(Que* pq); queue.c:
#define _CRT_SECURE_NO_WARNINGS #include "queue.h" //初始化队列结构 void QueueInit(Que* pq) { assert(pq); pq->phead = pq->ptail = NULL; pq->size = 0; } //队尾插入 void QNodePush(Que* pq, QDataType x) { assert(pq); QNode* newnode = (QNode*)malloc(sizeof(QNode)); if (newnode == NULL) { perror("malloc fail"); return; } newnode->data = x; newnode->next = NULL; //没有节点 if (pq->phead == NULL) { pq->phead = pq->ptail = newnode; } else//多个节点 { pq->ptail->next = newnode; pq->ptail = newnode; } pq->size++; } //队头删除 void QNodePop(Que* pq) { assert(pq); assert(pq->phead);//没有节点 //一个节点 if (pq->phead == pq->ptail) { free(pq->phead); pq->phead = pq->ptail = NULL; } //多个节点 else { QNode* next = pq->phead->next; free(pq->phead); pq->phead = next; } pq->size--; } //队列元素个数 int QNodeSize(Que* pq) { assert(pq); return pq->size; } //取队头 QDataType QNodeFront(Que* pq) { assert(pq); assert(pq->phead); return pq->phead->data; } //取队尾 QDataType QNodeBack(Que* pq) { assert(pq); assert(pq->ptail); return pq->ptail->data; } //判空 bool QNodeEmpty(Que* pq) { assert(pq); return pq->phead == NULL; } //销毁队列 void QNodeDestroy(Que* pq) { assert(pq); while (pq->phead) { QNode* next = pq->phead->next; free(pq->phead); pq->phead = next; } pq->ptail = NULL; pq->size = 0; } test.c:
#define _CRT_SECURE_NO_WARNINGS #include "queue.h" void test() { Que q; QueueInit(&q); QNodePush(&q, 1); QNodePush(&q, 2); QNodePush(&q, 3); QNodePush(&q, 4); QNodePop(&q); while (!QNodeEmpty(&q)) { printf("%d ", QNodeFront(&q)); //元素取完要删除 QNodePop(&q); } printf("\n"); QNodeDestroy(&q); } int main() { test(); return 0; } 总结
- 栈适合在需要临时存储、后进先出的场景下使用,特别在处理递归、嵌套、层次结构等问题时非常有用
- 栈的操作受限于其后进先出的特性,在处理大量数据、需要随机操作等情况下,不太适合使用栈
- 队列通常有一个固定的容量,一旦队列达到最大容量,后续元素无法入队,可能导致数据丢失或系统阻塞

