选择排序
之前文章分析了冒泡排序算法,其效率是O(N2)。现在我们再来探索另一种排序算法,选择排序,并将它跟冒泡排序对比一下。
选择排序的步骤如下。
(1) 从左至右检查数组的每个格子,找出值最小的那个。在此过程中,我们会用一个变量来记住检查过的数字的最小值(事实上记住的是索引,但为了看起来方便,下图就直接写出数值)。如果一个格子中的数字比记录的最小值还要小,就把变量改成该格子的索引,如图所示。

(2) 知道哪个格子的值最小之后,将该格与本次检查的起点交换。第1次检查的起点是索引0,第2次是索引1,以此类推。下图展示的是第一次检查后的交换动作。
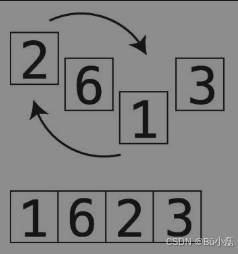
(3) 重复第(1) (2)步,直至数组排好序。
选择排序实战
以数组[4,2,7,1,3]为例,步骤如下。
开始第1轮检查。
首先读取索引0。根据此算法的定义,它是目前遇到的最小值(因为现在只检查了一个格子),于是记下其索引。

第1步:将索引1的值2与目前的最小值4进行比较。
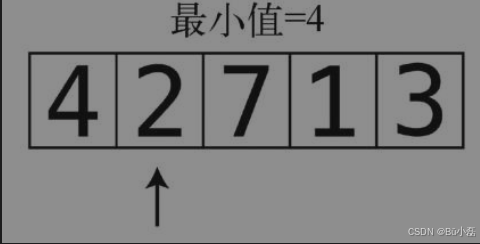
2比4还要小,于是将目前的最小值改为2。

第2步:再与下一个值做比较。因为7大于2,所以最小值还是2。

第3步:将1和目前的最小值做比较。

1比2还要小,于是目前的最小值更新为1。

第4步:比较3和目前的最小值1。因为现在已经走到数组尽头了,所以可以断定1是整个数组的最小值。

第5步:本次检查的起点是索引0,不管那里的值是什么,我们都应该将最小值1换到那里。
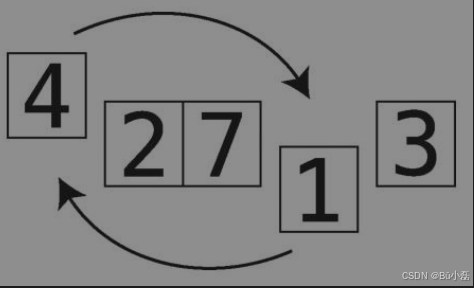
现在1就排到正确的位置上了。

可以开始第2轮检查了。准备工作:因为索引0的值已符合其排位,所以这一轮从下一个格子开始,即索引1,其值为2,也是目前本轮所遇到的最小值。

第6步:将7跟目前的最小值2进行比较。因为2小于7,所以最小值仍为2。

第7步:将4跟目前的最小值2进行比较。因为2小于4,所以最小值仍为2。

第8步:将3跟目前的最小值2进行比较。因为2小于3,所以最小值仍为2。

又走到数组尽头了。本轮不需要做任何交换,2已在其正确位置上。于是第2轮检查结束,现在数组如下图所示。

开始第3轮检查。准备工作:从索引2起,其值为7。于是本轮目前最小值为7。

第9步:比较4与7。

将4记为目前的最小值。

第10步:遇到3,它比4还小。

于是3成了目前的最小值。

第11步:到数组尽头了,将3跟本轮起点7进行交换。

于是3排到正确位置上了。

虽然我们可以看到现在整个数组都有序了,但计算机是看不到的,它只会继续第4轮检查。
准备工作:此轮检查从索引3开始,其值4是目前的最小值。

第12步:比较4和7。

4仍为最小值,而且它也处于本轮起点,因此无须任何交换。
因为最后一个格子左侧的那些值都已在各自的正确位置上,所以最后一格也必然正确,于是排序结束。

以上是选择排序的一个模拟实战,通过上面的演示更容易理解排序的过程,下篇博客会写一个代码实现选择排序。
