阅读量:3
目录
这次周赛题目比较简单,算法题也基本上是板子题,出得很好(~ ̄▽ ̄)~
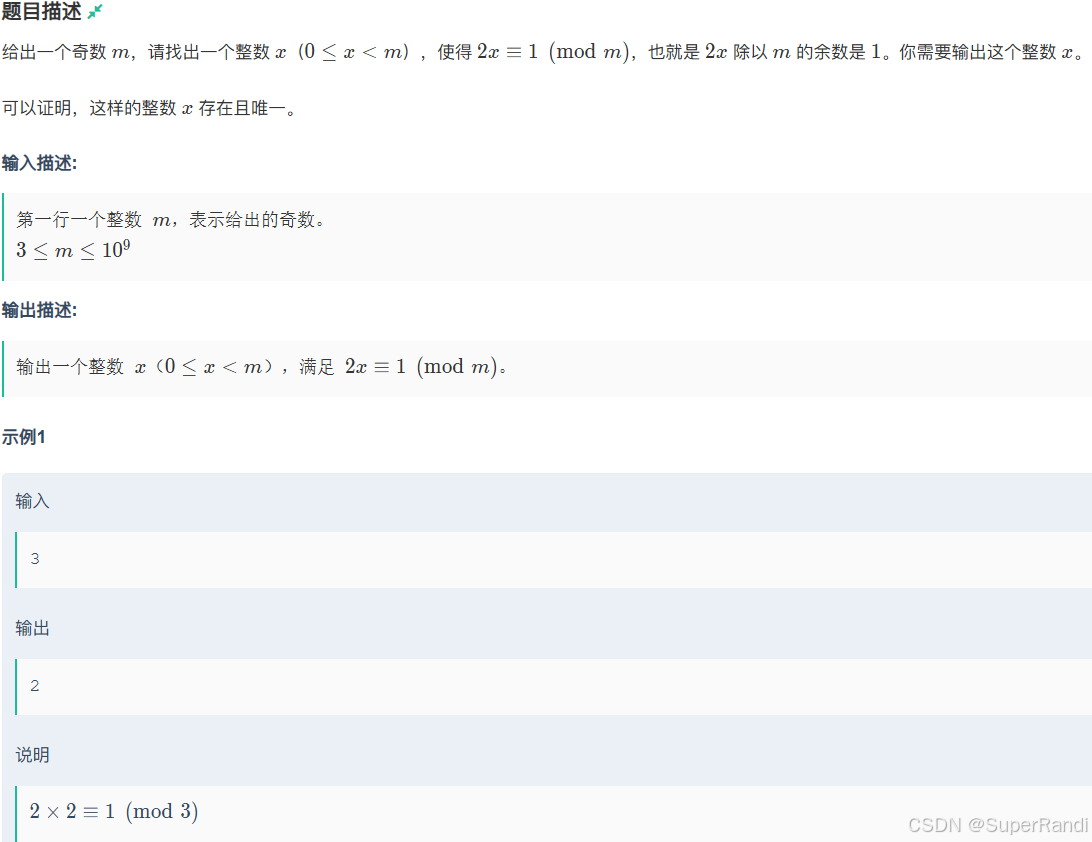
A.小红的同余
思路:签到题,别看成逆元题就行
#include<iostream> #define int long long using namespace std; int32_t main() { int m;cin>>m; cout<<(m+1)/2; }B.小红的三倍数
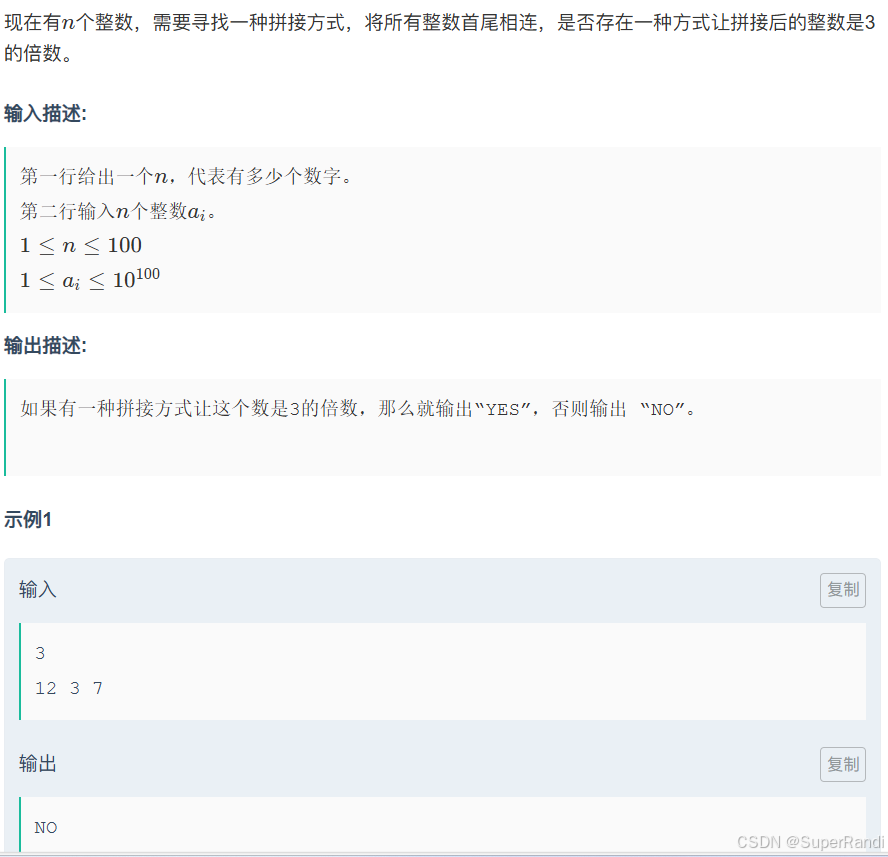
思路:签到题,如果这个数能被三整除,则这个数每一位的数相加得到的和也能被三整除
#include<iostream> #include<cstring> using namespace std; int main() { int n;cin>>n; int sum=0; for(int i=0;i<n;i++) { string s;cin>>s; for(int j=0;j<s.size();j++) { sum+=s[j]-'0'; } } if(sum%3==0) puts("YES"); else puts("NO"); }C.小红充电
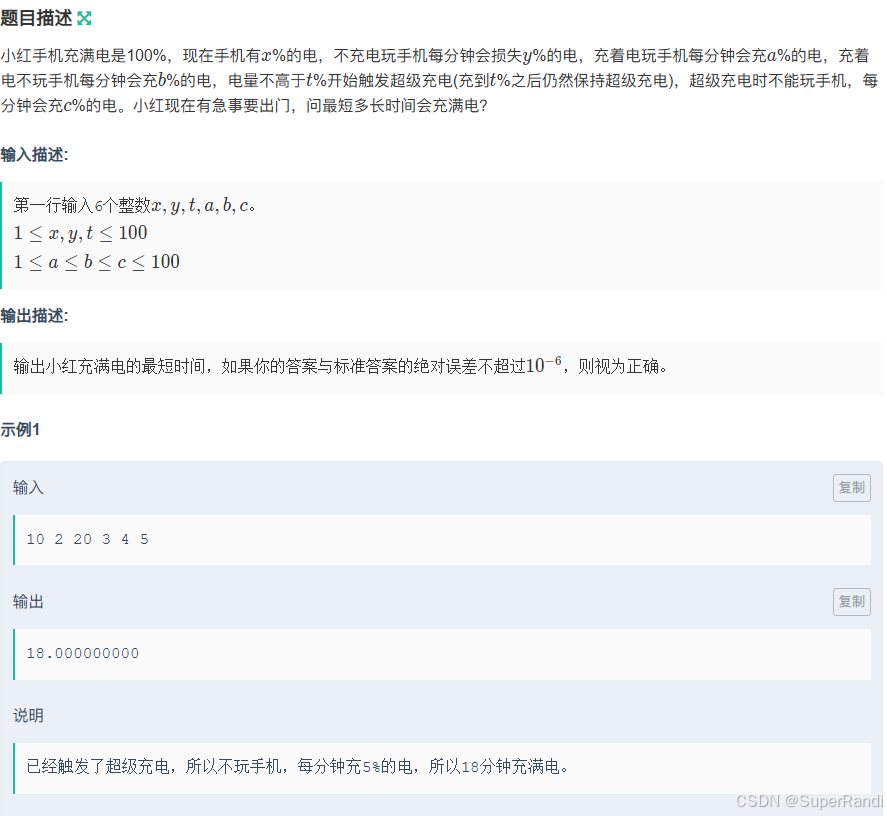
思路:总共分两种情况讨论:
① x<=t 时使用超级快充即可
② x>t 时,计算先玩到电量为t时启用超级快充更快还是直接充电更快
#include<iostream> using namespace std; int main() { double x,y,t,a,b,c;cin>>x>>y>>t>>a>>b>>c; if(x<=t) { printf("%.9lf",(100*1.0-x)/c); } else { double wan=x-t; double t1=1.0*wan/y;//这个地方分母要乘1.0 double t2=(100*1.0-t)/c; double t3=(t1+t2); double t4=(100*1.0-x)/b; printf("%.9lf",min(t3,t4)); } }D.小红的gcd
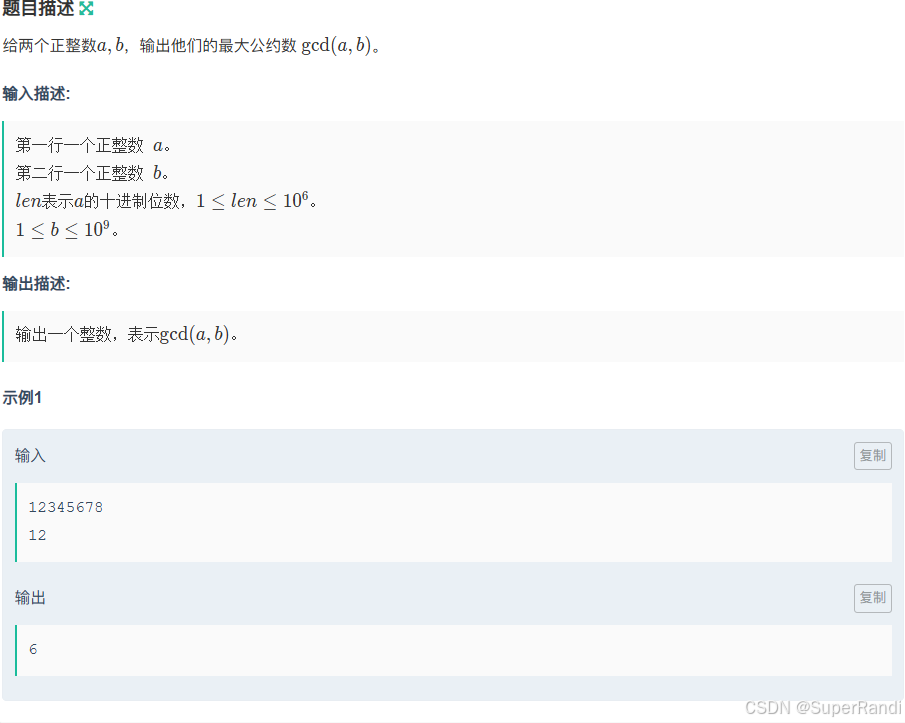
思路:可以迭代线性遍历a,来求解a%b的值,然后在求gcd(a%b, b)
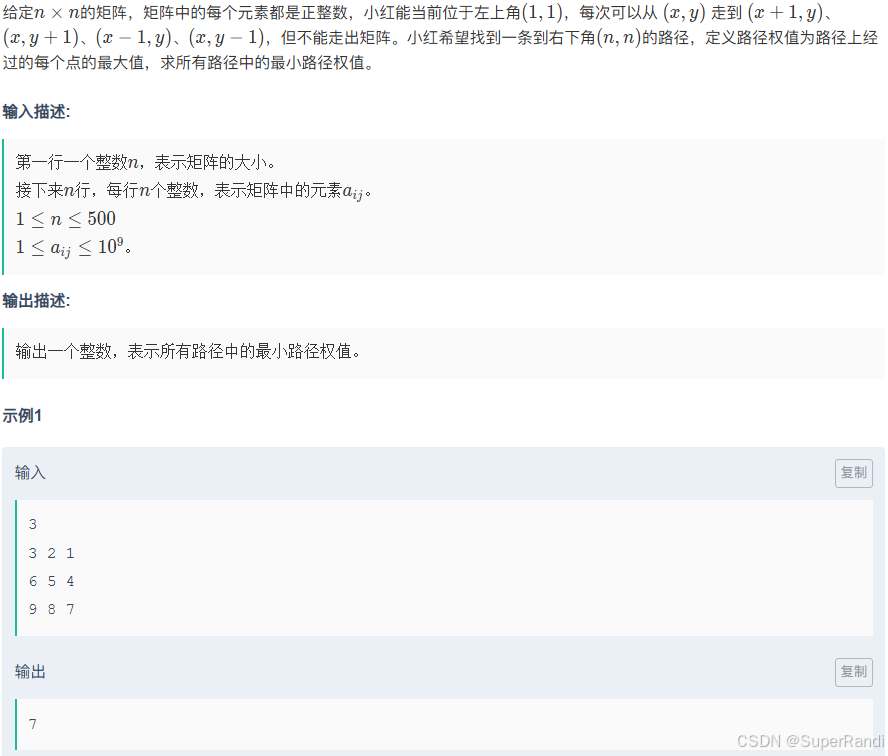
#include<iostream> #define int long long using namespace std; int gcd(int a,int b) { return b?gcd(b,a%b):a; } int32_t main() { string a;cin>>a; int b;cin>>b; int res=0; for(auto t:a) { res=(res*10+(t-'0'))%b; } cout<<gcd(res,b); }E.小红走矩阵
思路:用Dijkstra来写,优先队列每次弹出所有路径最大值的最小值
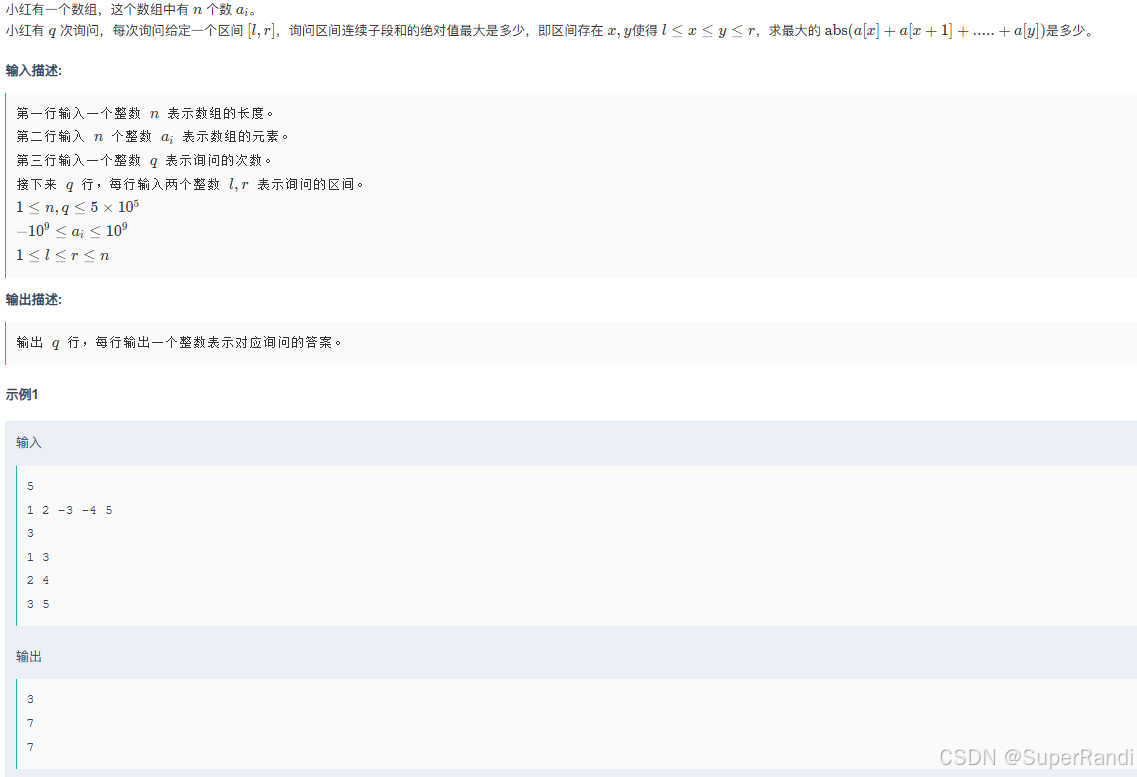
#include<iostream> #include<vector> #include<queue> #define x first #define y second using namespace std; typedef pair<int,int> PII; typedef pair<int,PII> PIII; const int N=505; int ne[4][2]={{0,1},{0,-1},{1,0},{-1,0}}; int a[N][N],n,dist[N][N]; bool st[N][N]; void Dijkstra() { priority_queue<PIII,vector<PIII>,greater<PIII>> heap; heap.push({a[1][1],{1,1}}); dist[1][1]=a[1][1]; while(heap.size()) { auto it=heap.top();heap.pop(); int xx=it.y.x,yy=it.y.y,ma=it.x; if(st[xx][yy]) continue; st[xx][yy]=true; for(int i=0;i<4;i++) { int tx=xx+ne[i][0],ty=yy+ne[i][1]; if(tx>=1&&tx<=n&&ty>=1&&ty<=n&&!st[tx][ty]) { dist[tx][ty]=max(ma,a[tx][ty]); heap.push({dist[tx][ty],{tx,ty}}); } } } } int main() { cin>>n; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>a[i][j]; Dijkstra(); cout<<dist[n][n]; }F.小红的数组
思路: 线段树板题,跟“你能回答这些问题吗”做法一样,只是多了一个要存储每个区间的最小线段和,这里得用scanf输入才不会超时,关闭流用cin,cout还是会超时
#include<iostream> #define int long long using namespace std; const int N=5e5+5; int w[N]; struct node{ int l,r; int sum,sum_min; int lmax,lmin; int rmax,rmin; int tmax,tmin; }tr[4*N]; void pushup(node &u,node &l,node &r) { u.sum=l.sum+r.sum; u.lmax=max(l.lmax,l.sum+r.lmax); u.rmax=max(r.rmax,r.sum+l.rmax); u.tmax=max(max(l.tmax,r.tmax),l.rmax+r.lmax); u.sum_min=l.sum_min+r.sum_min; u.lmin=min(l.lmin,l.sum_min+r.lmin); u.rmin=min(r.rmin,r.sum_min+l.rmin); u.tmin=min(min(l.tmin,r.tmin),l.rmin+r.lmin); } void pushup(int u) { pushup(tr[u],tr[u<<1],tr[u<<1|1]); } void build(int u,int l,int r) { if(l==r) tr[u]={l,l,w[l],w[l],w[l],w[l],w[l],w[l],w[l],w[l]}; else { tr[u]={l,r}; int mid=(l+r)>>1; build(u<<1,l,mid),build(u<<1|1,mid+1,r); pushup(u); } } node query(int u,int l,int r) { if(tr[u].l>=l&&tr[u].r<=r) return tr[u]; else { int mid=(tr[u].l+tr[u].r)>>1; if(mid>=r) return query(u<<1,l,r); else if(mid<l) return query(u<<1|1,l,r); else { node L=query(u<<1,l,r); node R=query(u<<1|1,l,r); node res; pushup(res,L,R); return res; } } } int32_t main() { int n;scanf("%lld",&n); for(int i=1;i<=n;i++) scanf("%lld",&w[i]); build(1,1,n); int q;scanf("%lld",&q); while(q--) { int l,r;scanf("%lld %lld",&l,&r); node res=query(1,l,r); printf("%lld\n",max(abs(res.tmax),abs(res.tmin))); } }