阅读量:3
目录
1.查找

1.查找的基本概念
1.在哪里找?

2.什么查找?

3.查找成功与否?

4.查找的目的是什么?

5.查找表怎么分类?

6.如何评价查找算法?

7.查找的过程中我们要研究什么?

2.线性表的查找

1.顺序查找


代码示例:
typedef struct { int key; }elem; typedef struct { elem *r; int len; }sstable; sstable st; int search_seq(sstable st,int key) { for(int i = st.len; i >= 1; --i) { if(st.r[i].key == key) return i; return 0; } }
1.顺序查找的改进



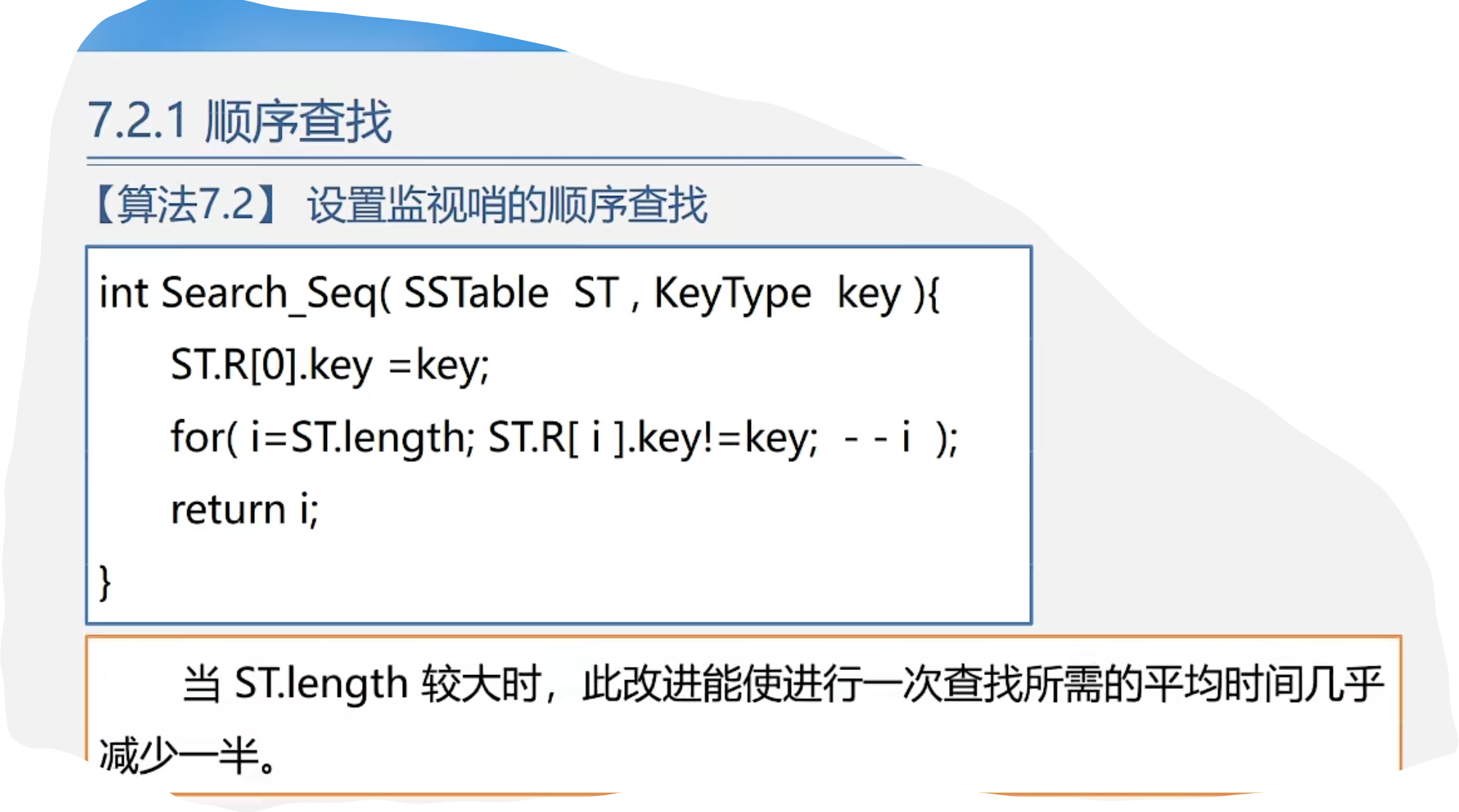
代码示例:
int Search_seq(sstable st,int key) { st.r[0].key = key; int i; for(i = st.len; st.r[i].key != key; --i); return i; }
2.顺序查找的性能分析与特点
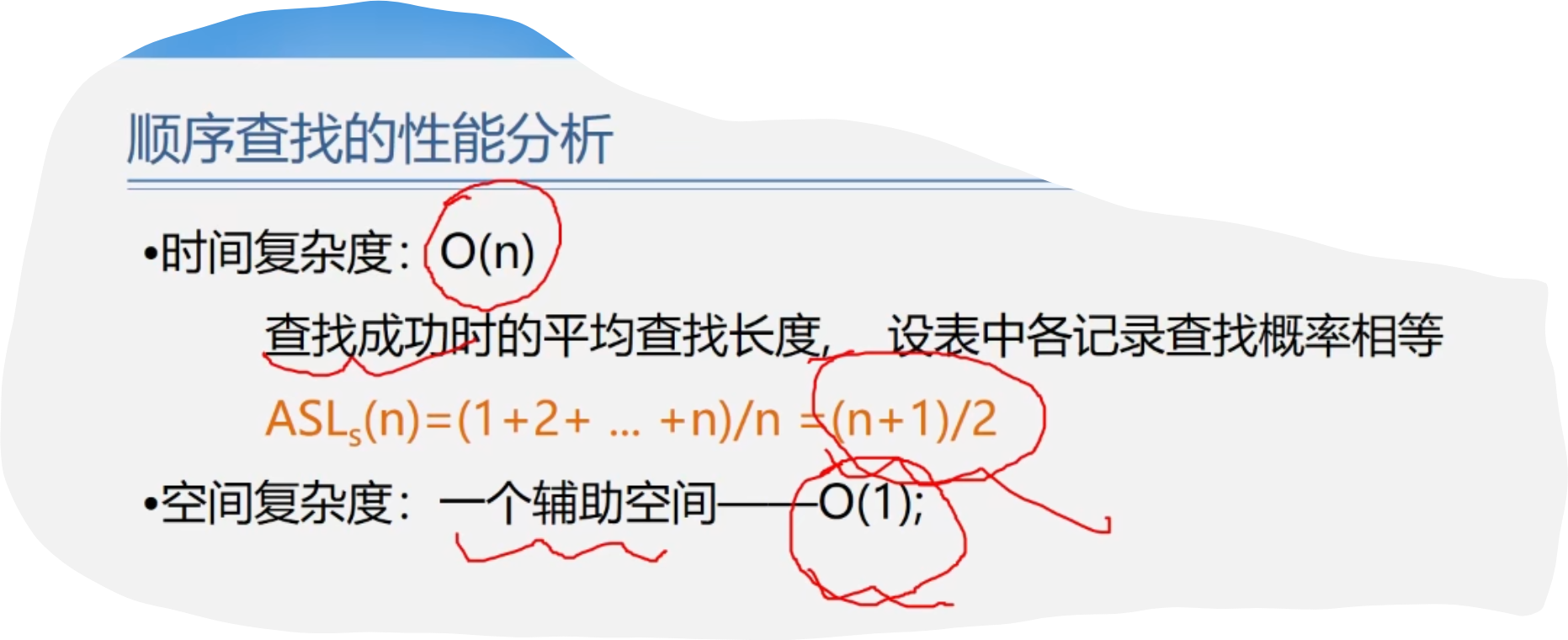
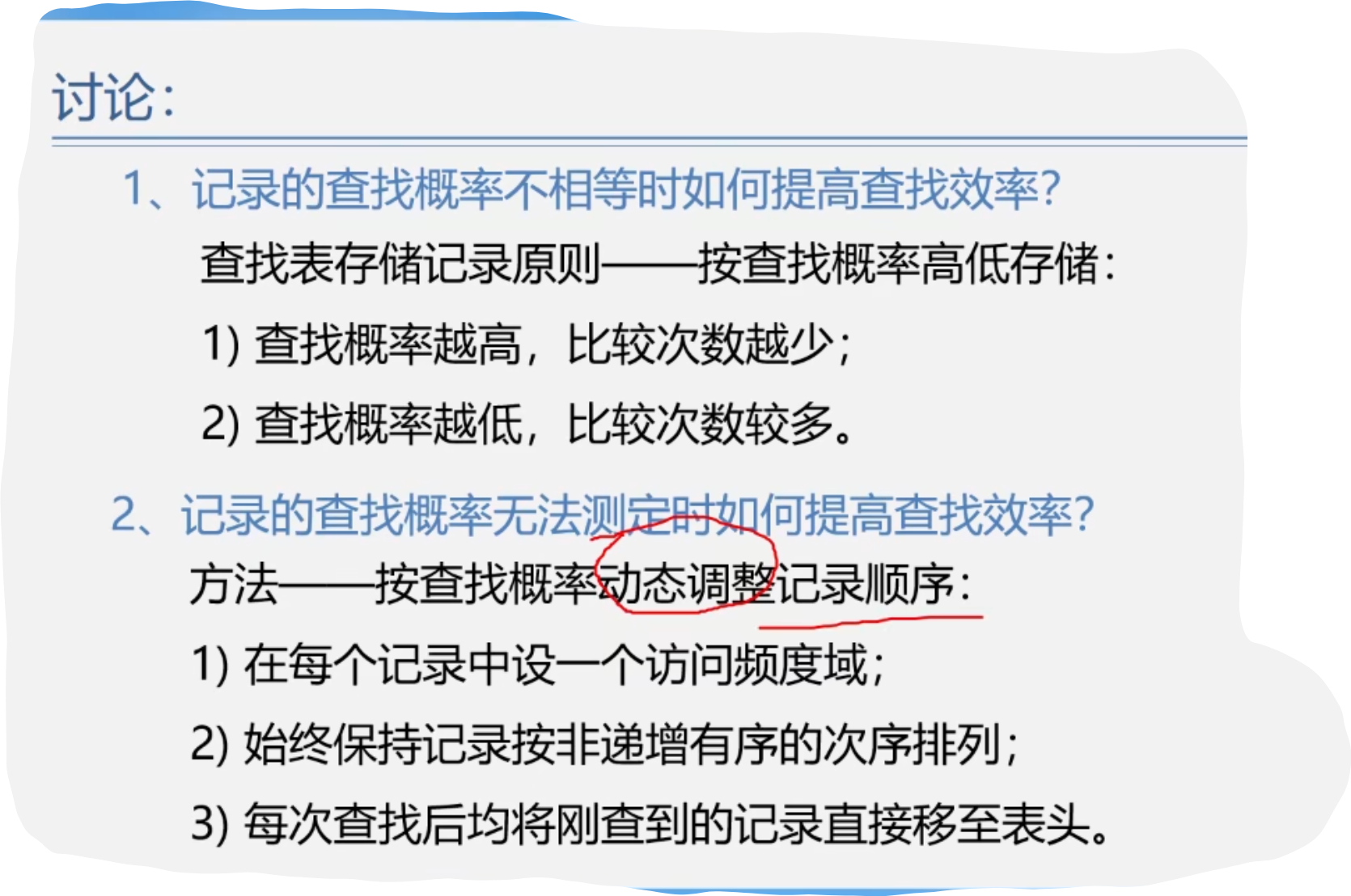


2.折半查找
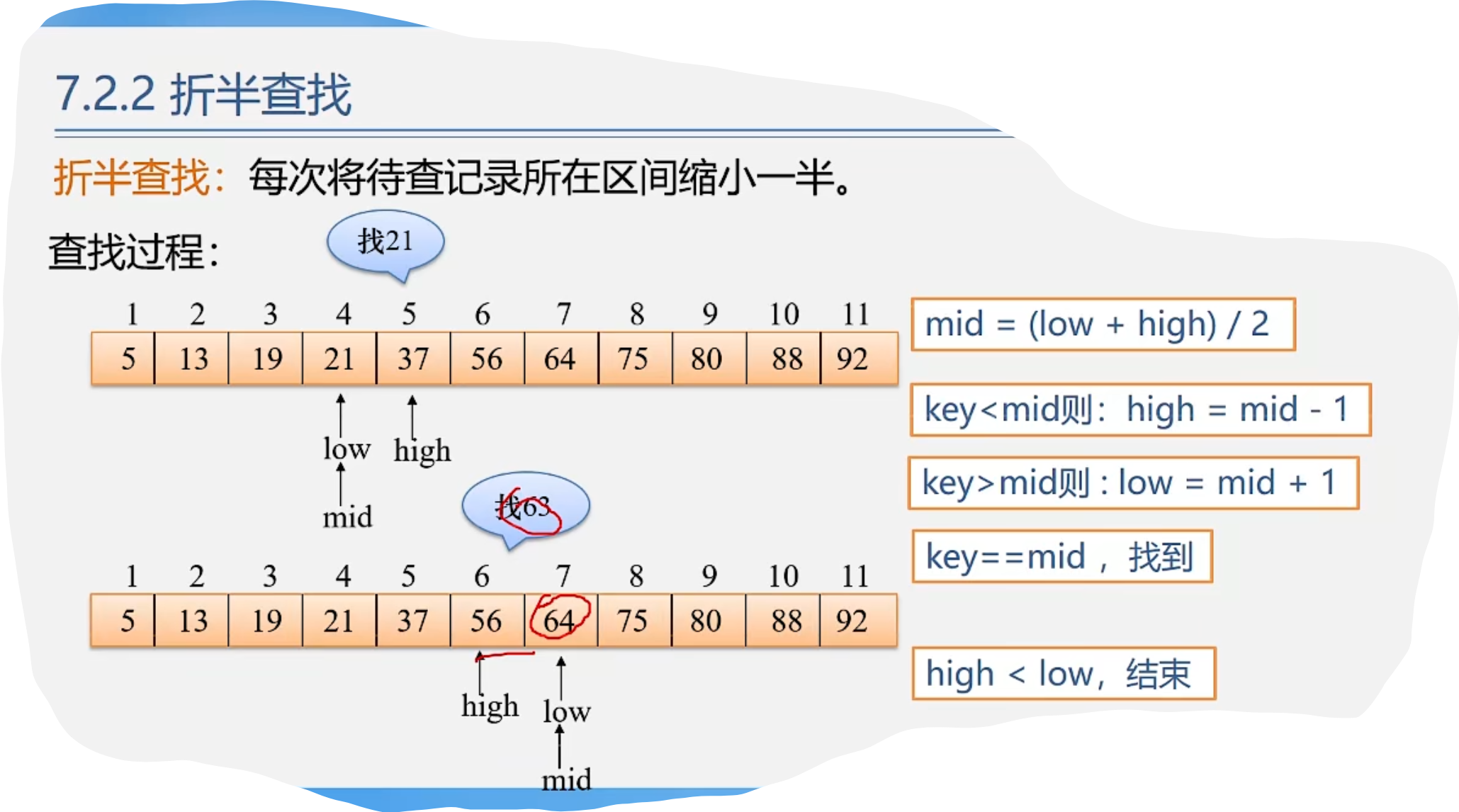



代码示例:
int search_bin(sstable st,int key) { int low = 1; int high = st.len; while(low <= high) { int mid = (low + high) / 2; if(st.r[mid].key == key) return mid; else if(key < st.r[mid].key) high = mid - 1; else low = mid + 1; } return 0; }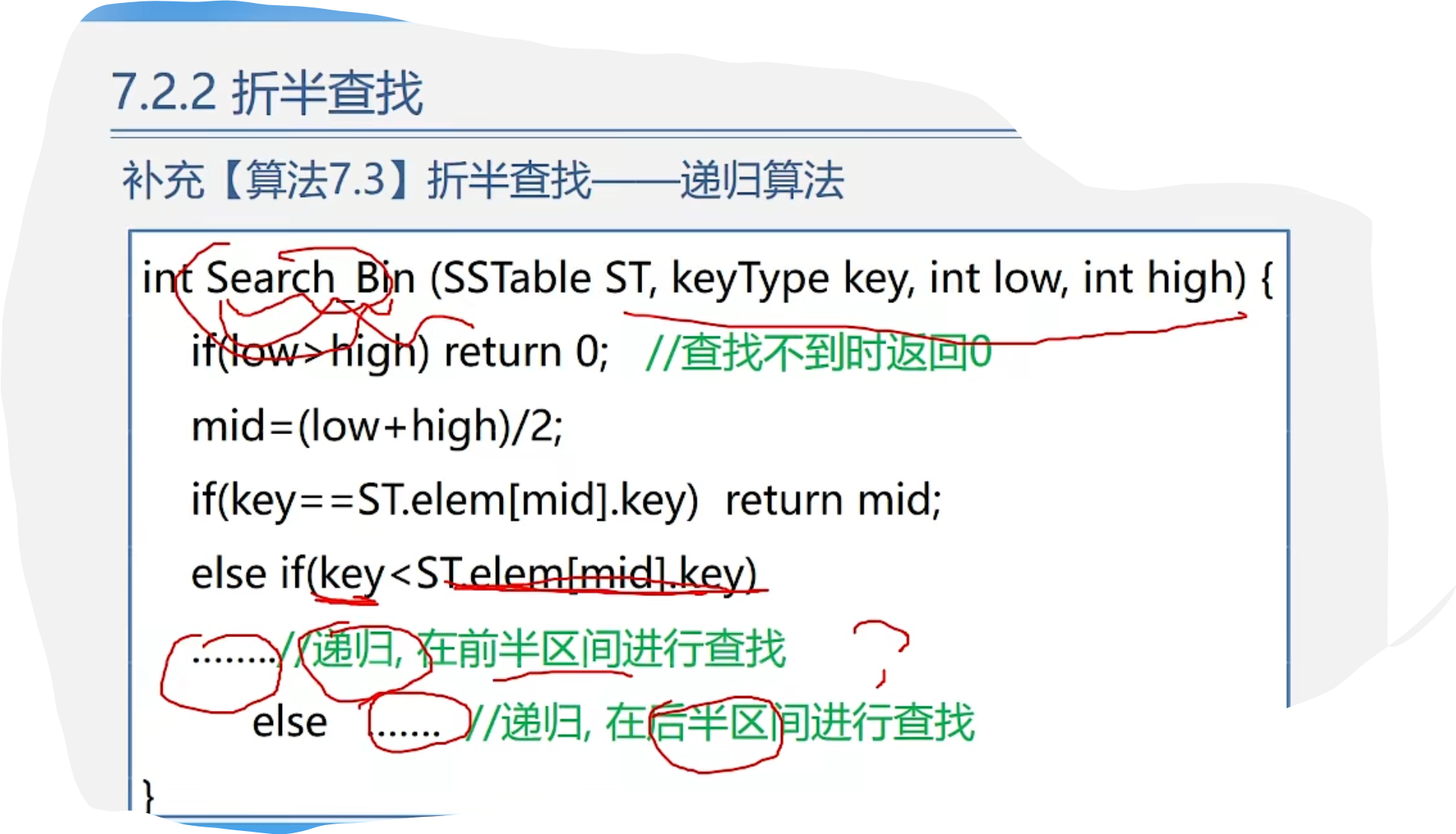
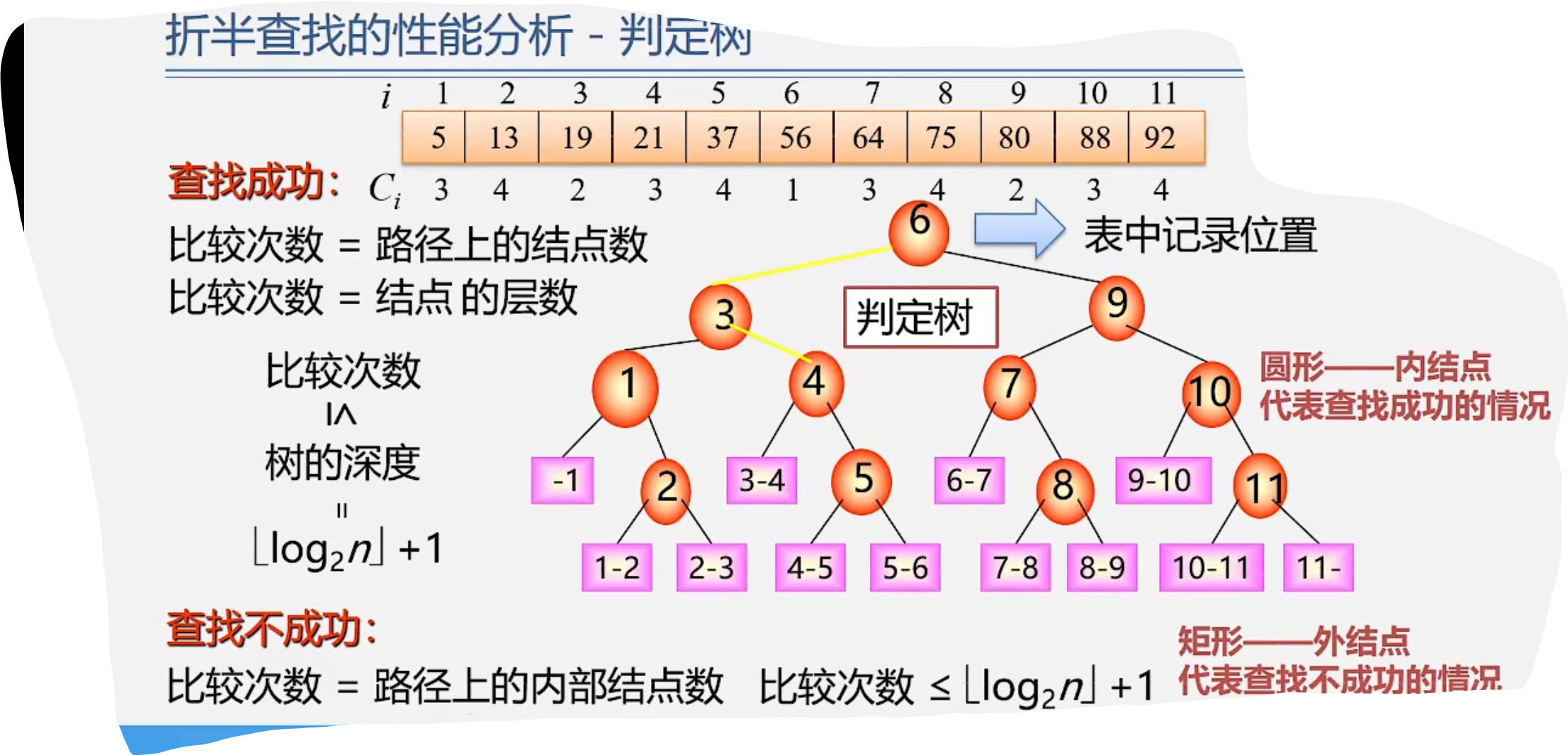
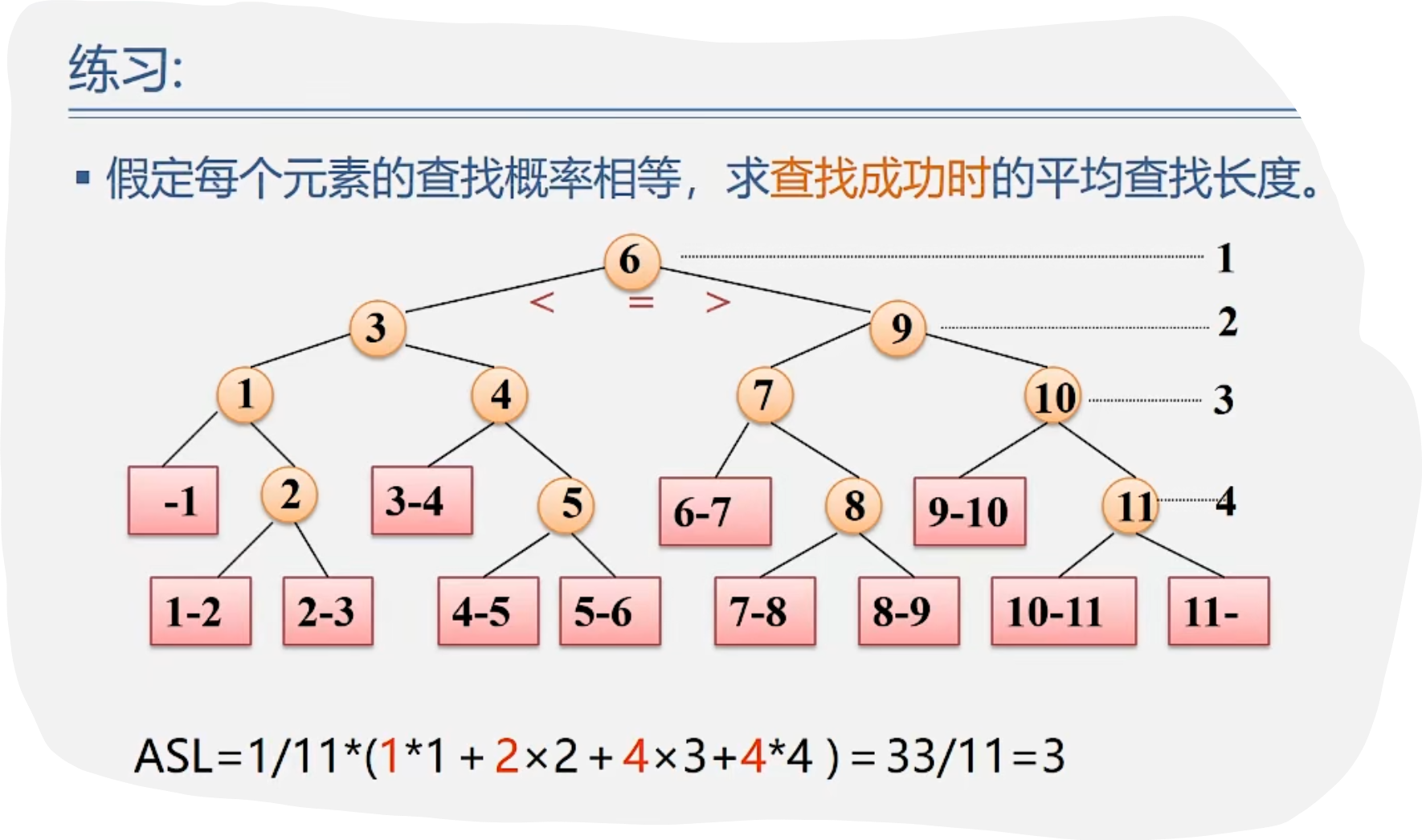
1.折半查找的性能分析与特点

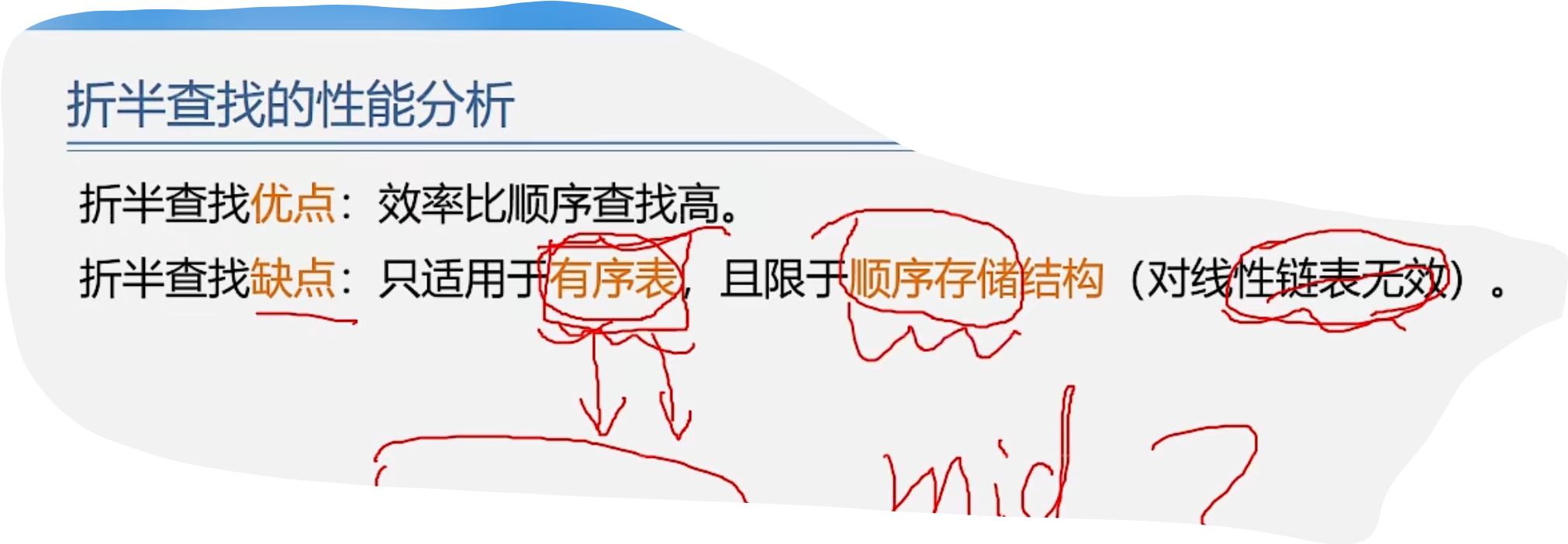

3.分块查找(索引顺序查找)

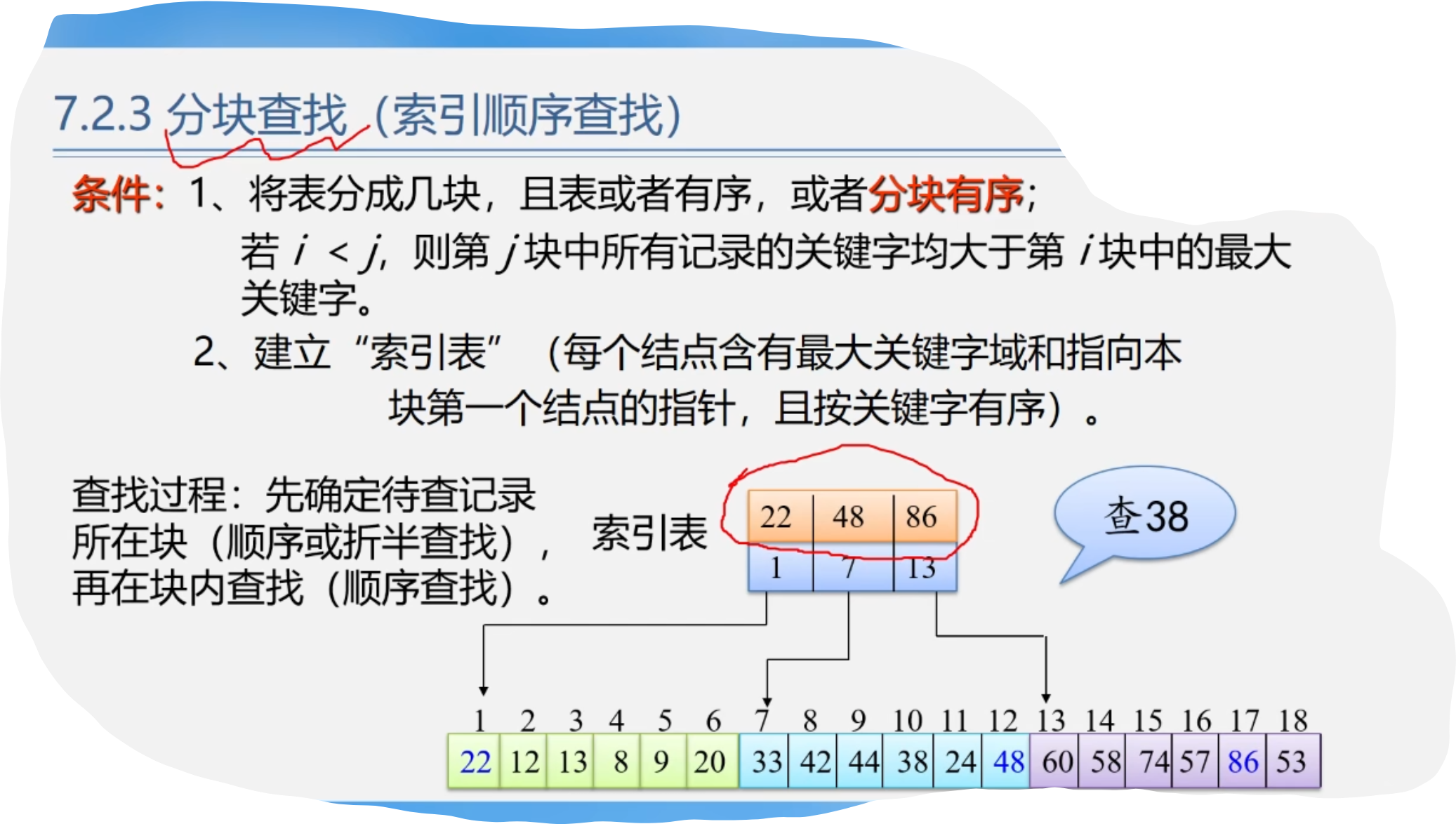
1.分块查找性能分析与优缺点
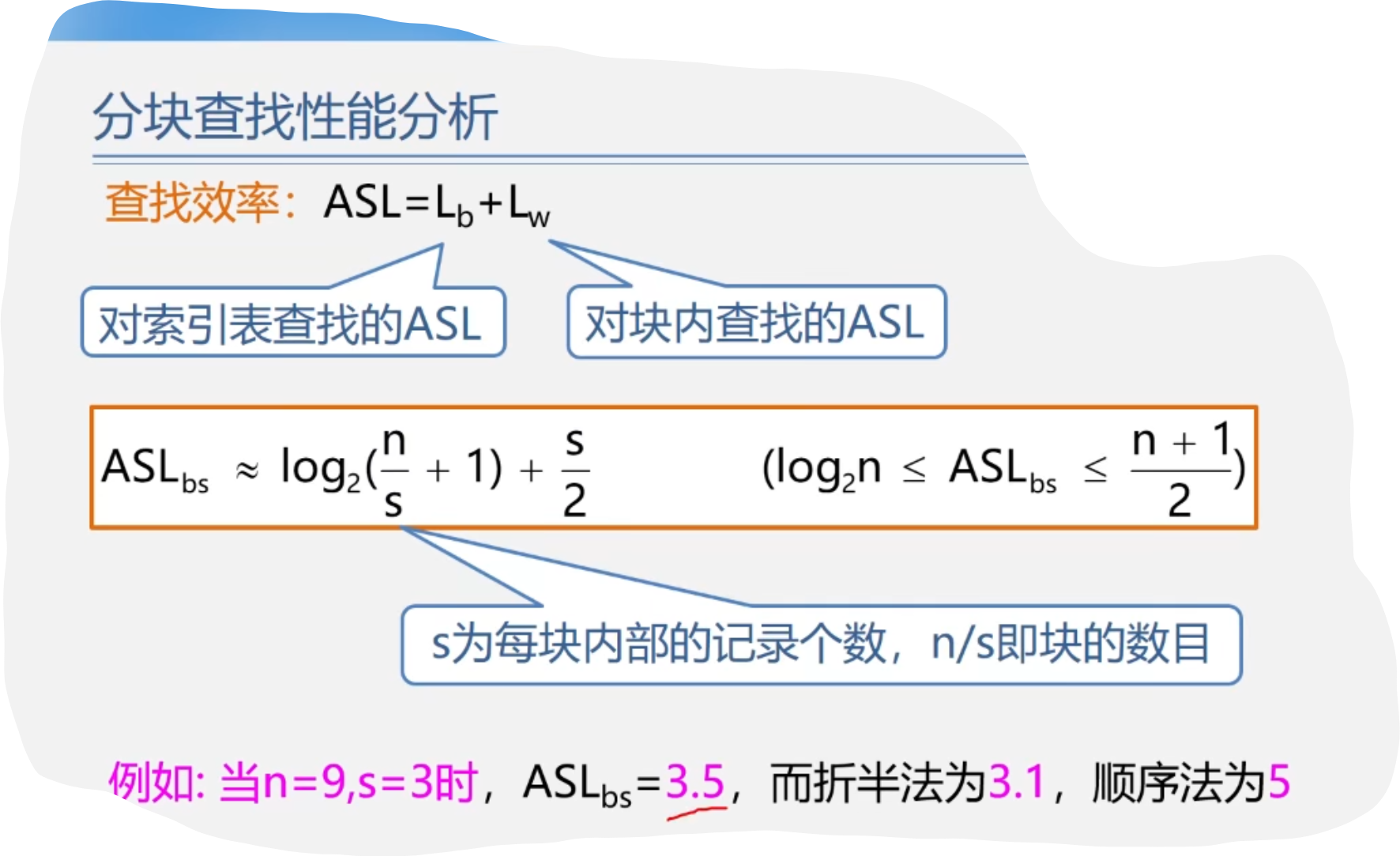
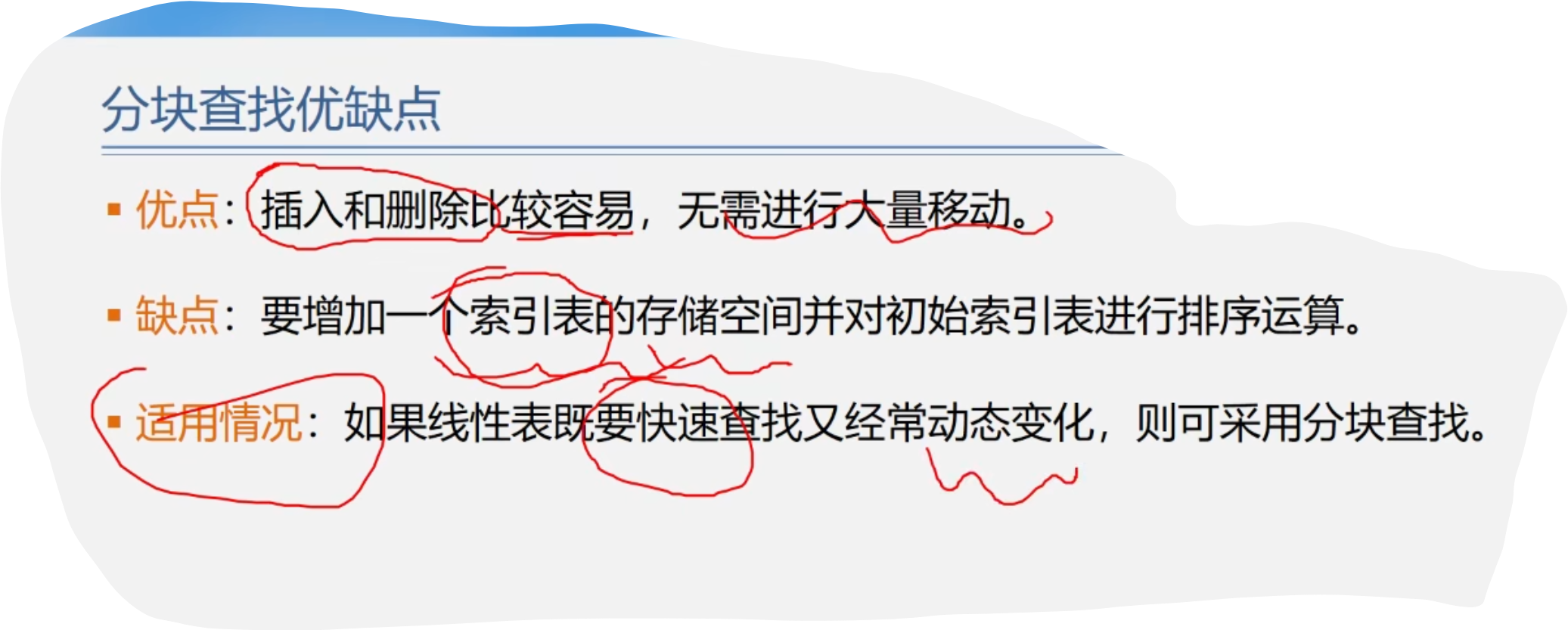

3.树表的查找
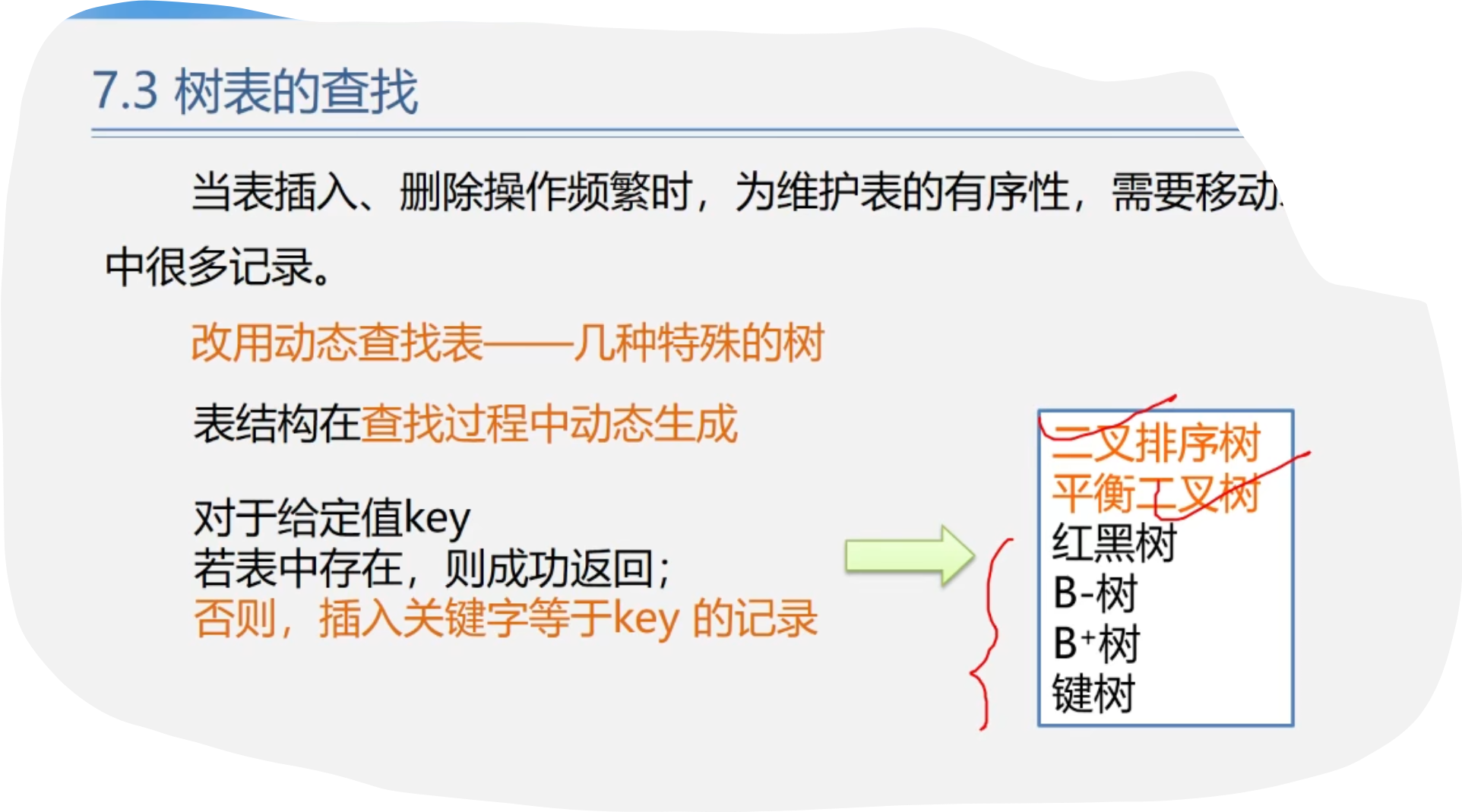
1.二叉排序树
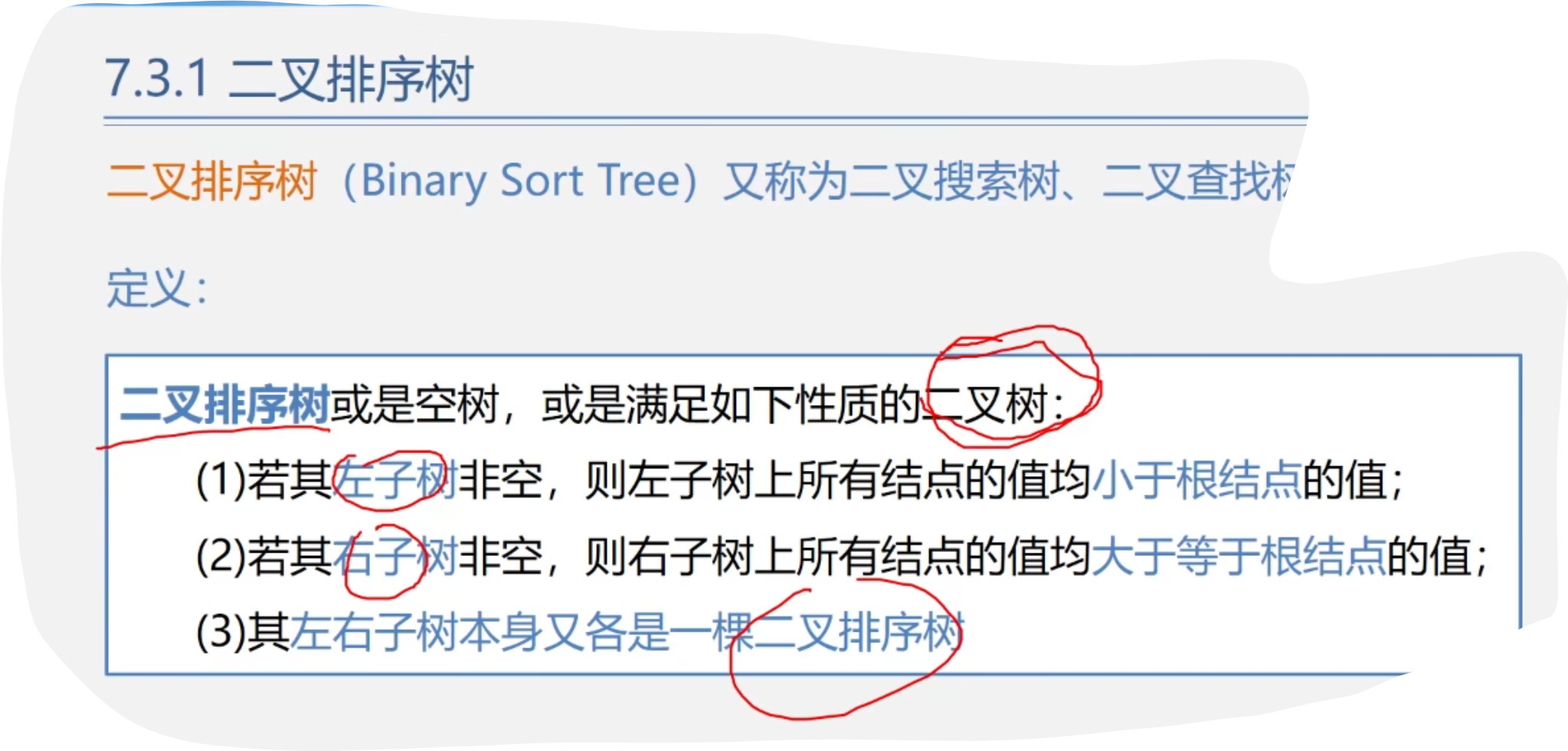
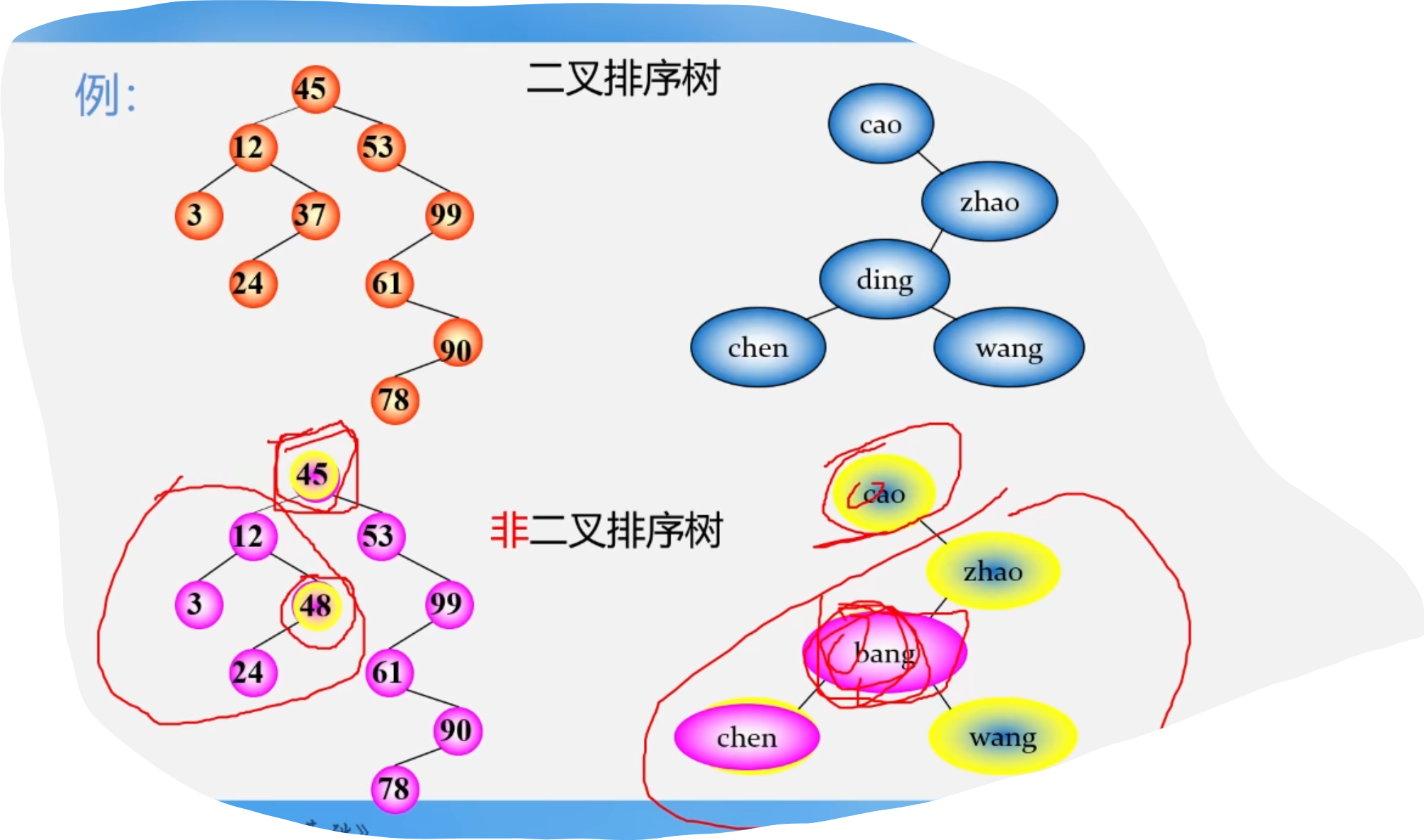
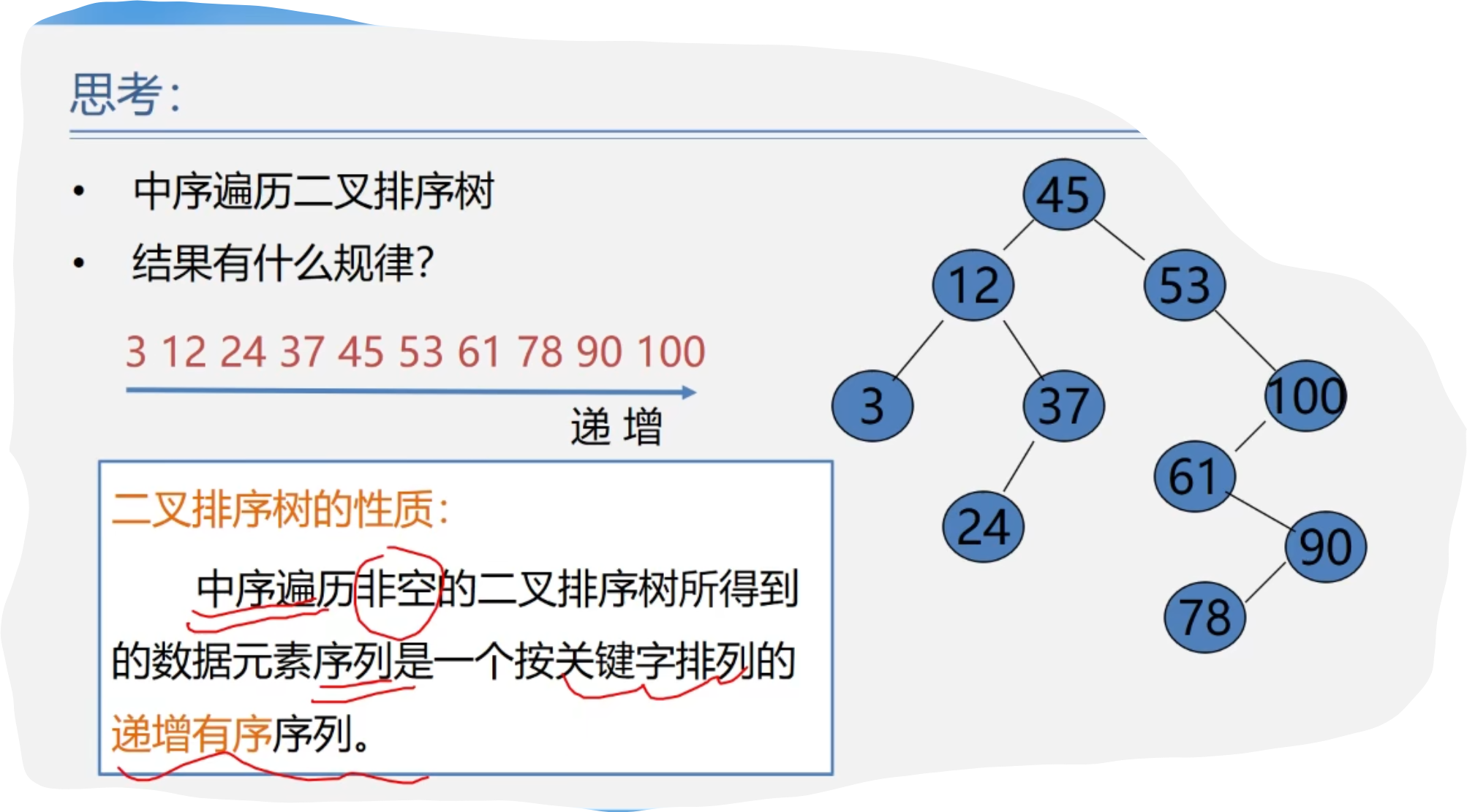
1.二叉排序树的存储结构

代码示例:
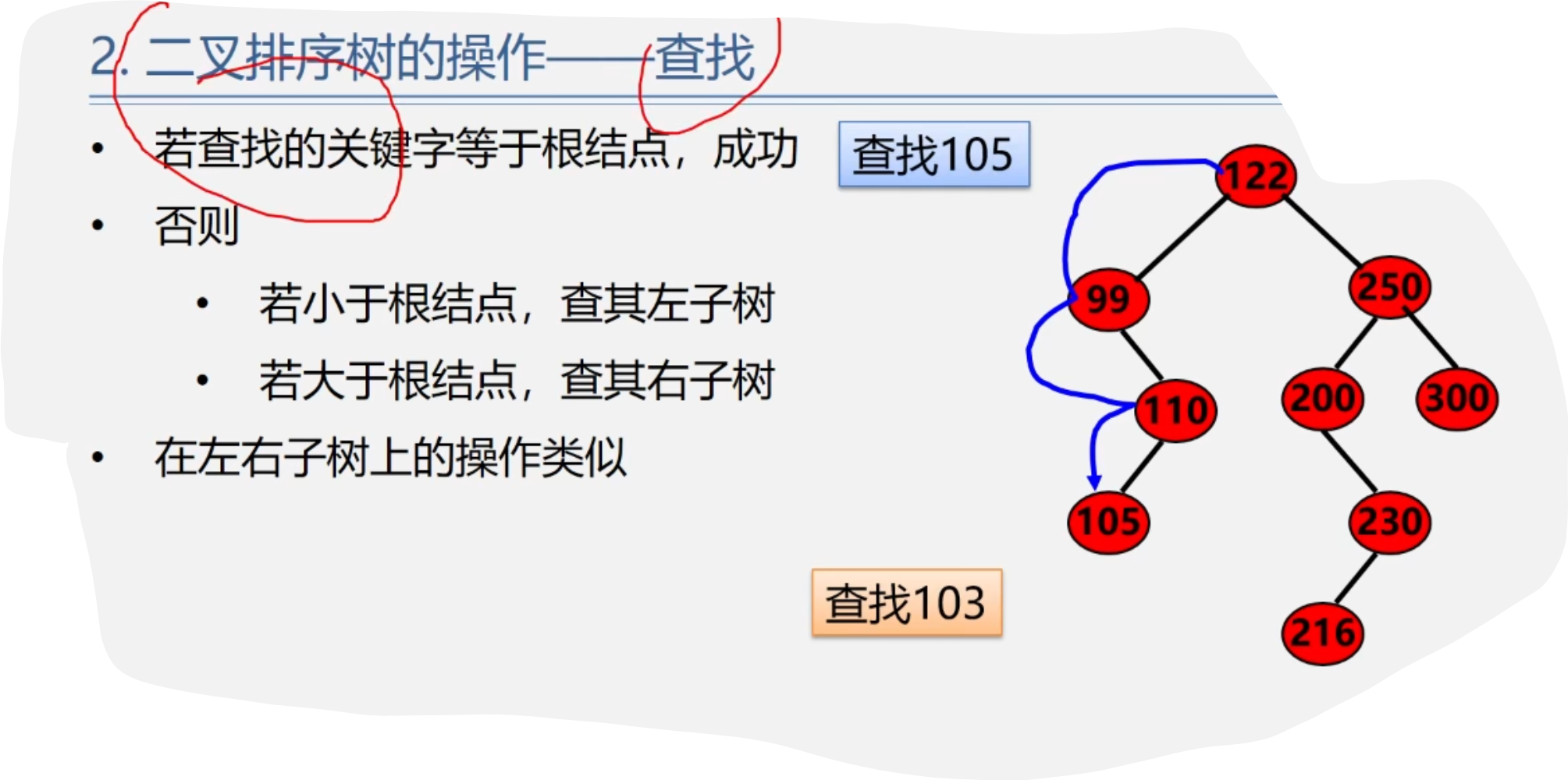
typedef struct { int key; }elemtype; typedef struct bstnode { elemtype data; struct bstnode *lchild, *rchild; }bstnode,*bstree; bstree t;2.二叉排序树的递归查找
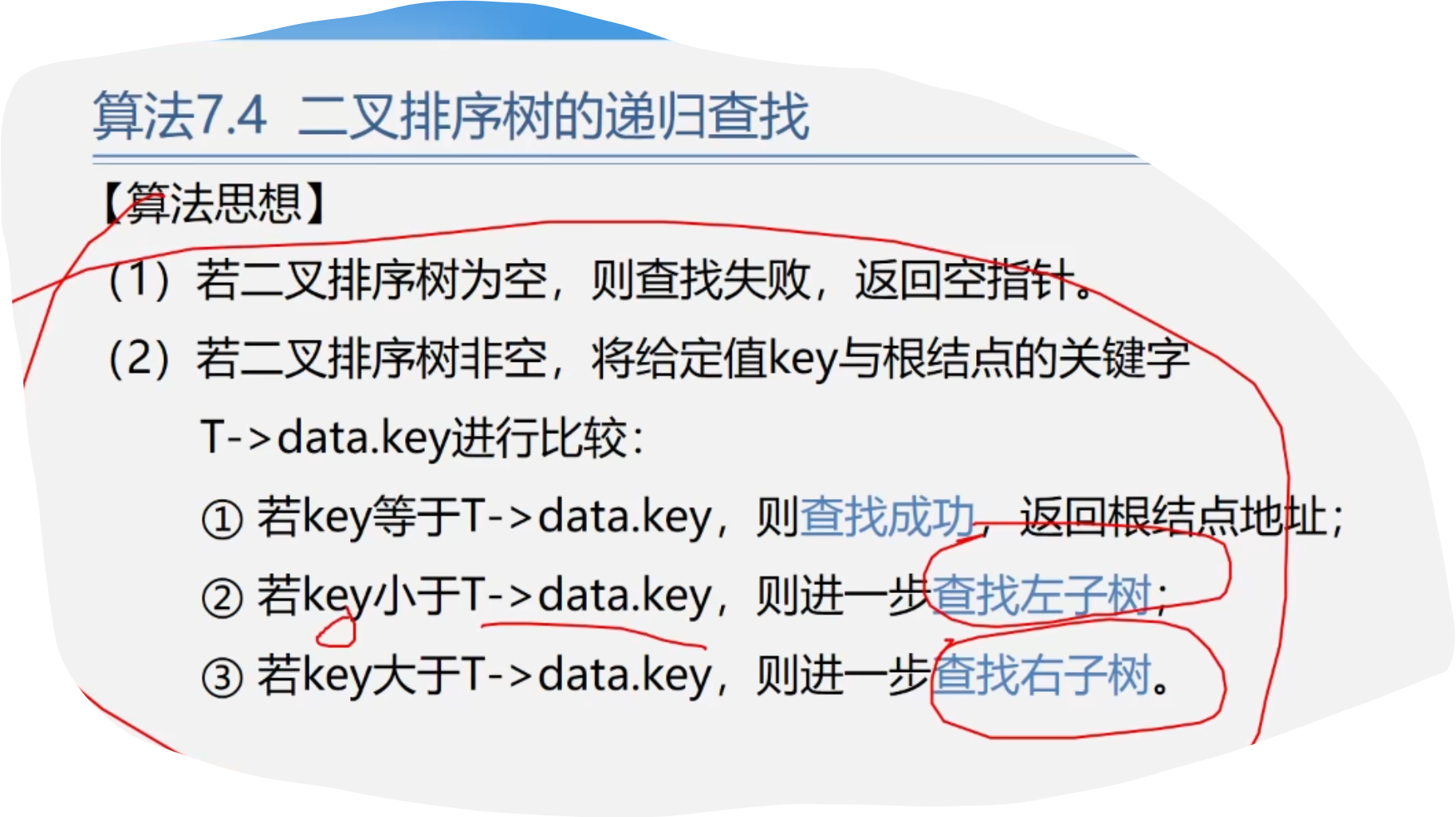
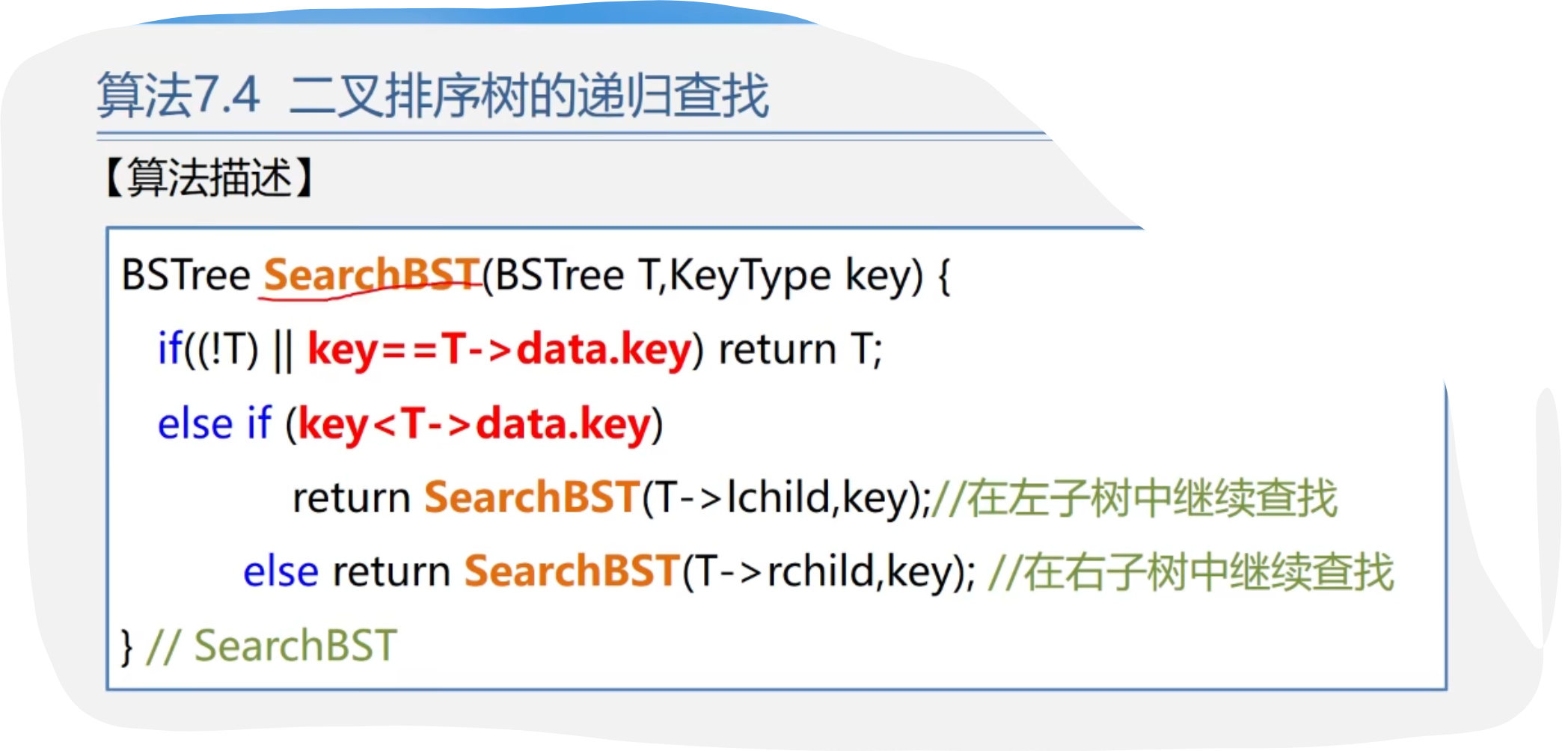
代码示例:
bstree searchbst(bstree t,int key) { if((!t) || key == t -> data.key) return t; else if(key < t -> data.key) return searchbst(t -> lchild,key); else return searchbst(t -> rchild,key); }3.二叉排序树的查找分析
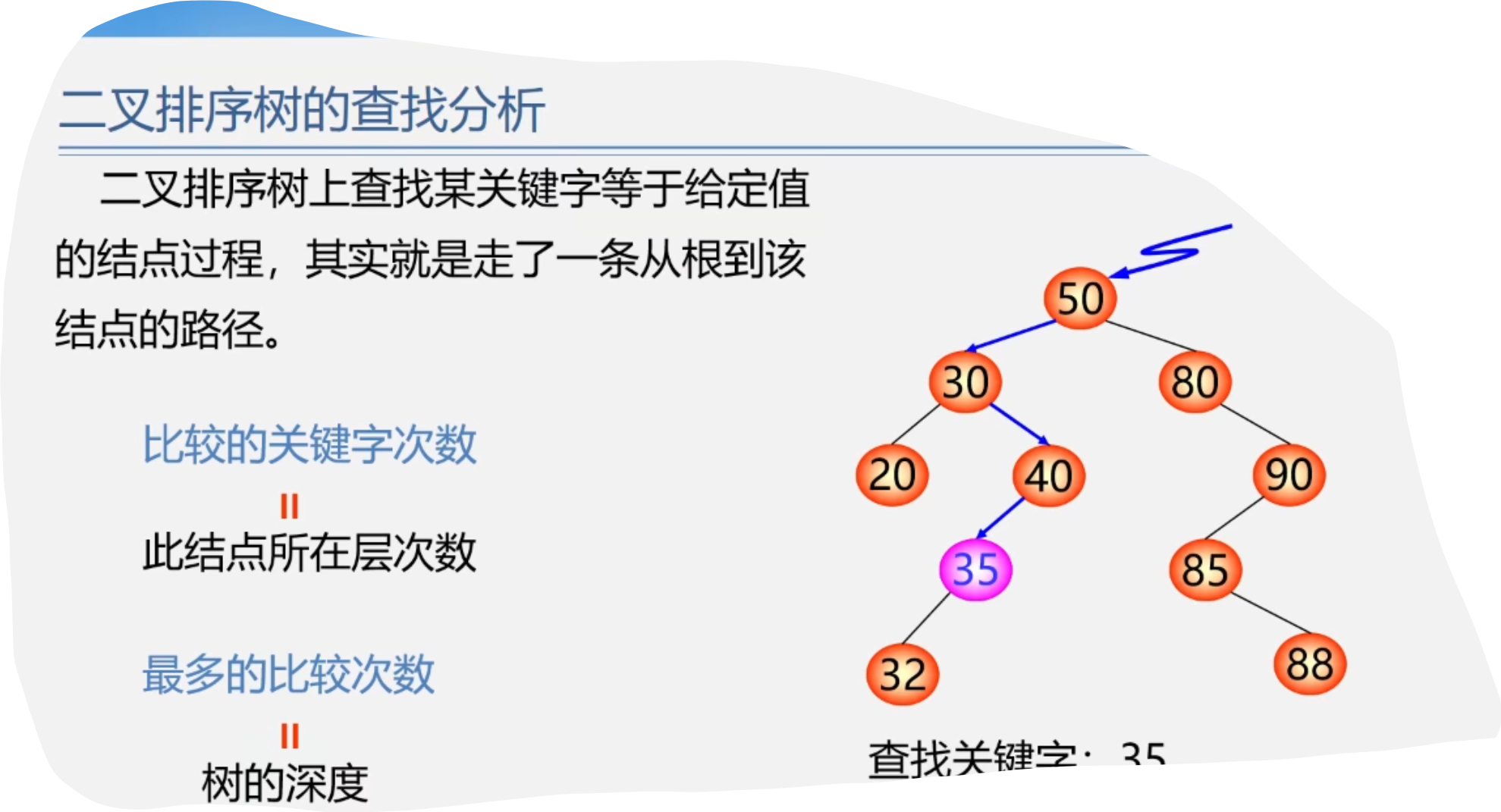
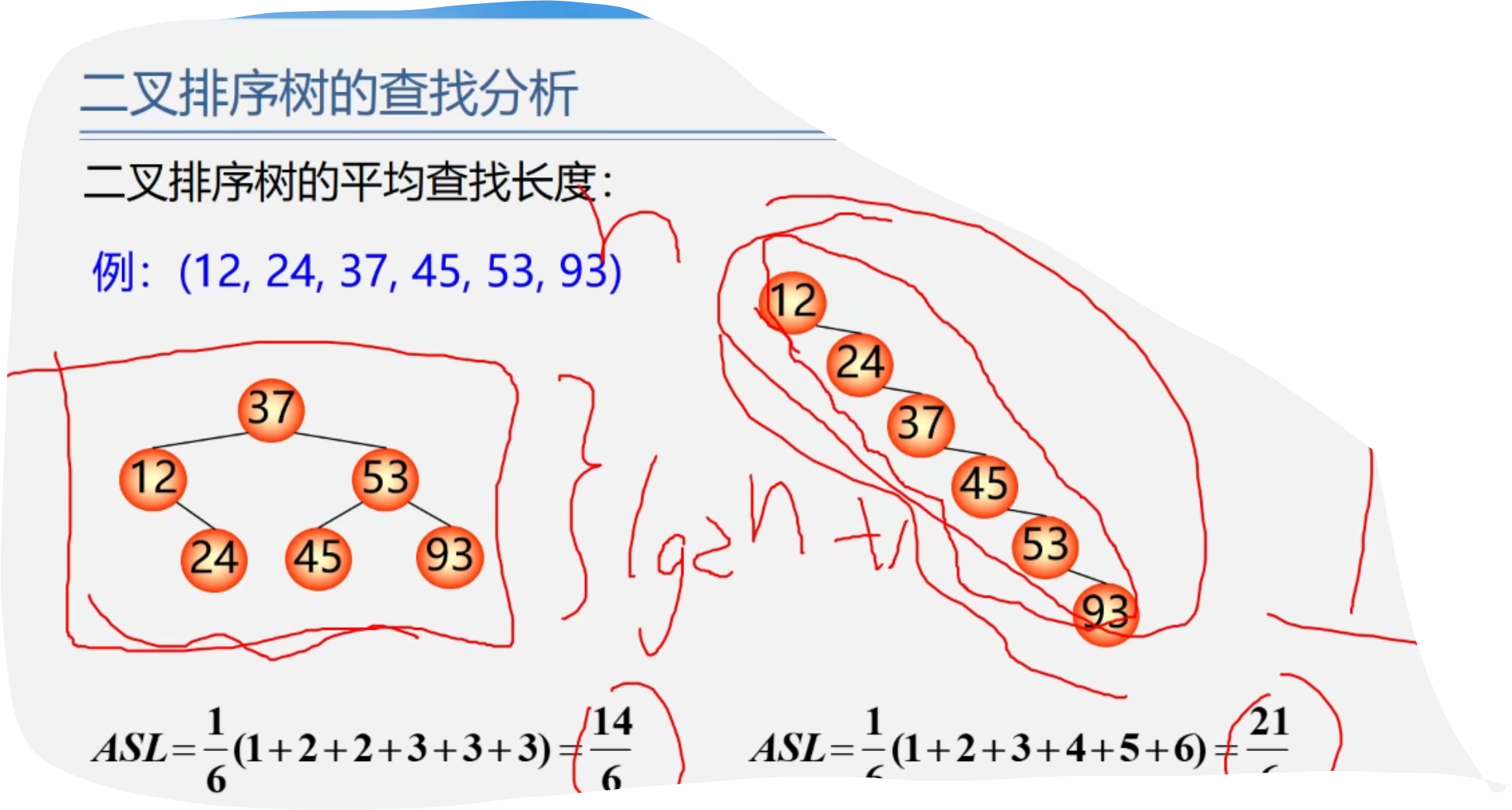

平衡二叉树

4.二叉排序数的操作-插入
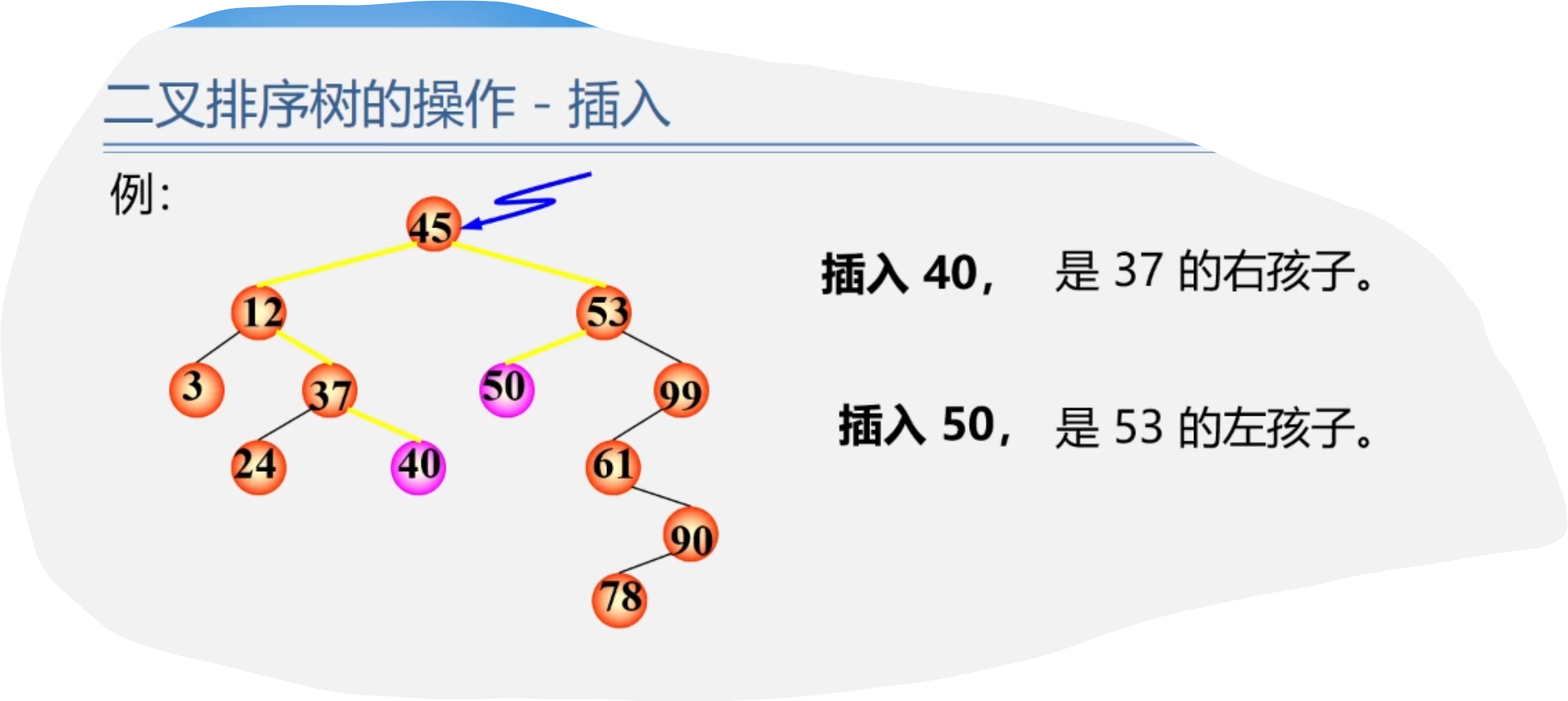


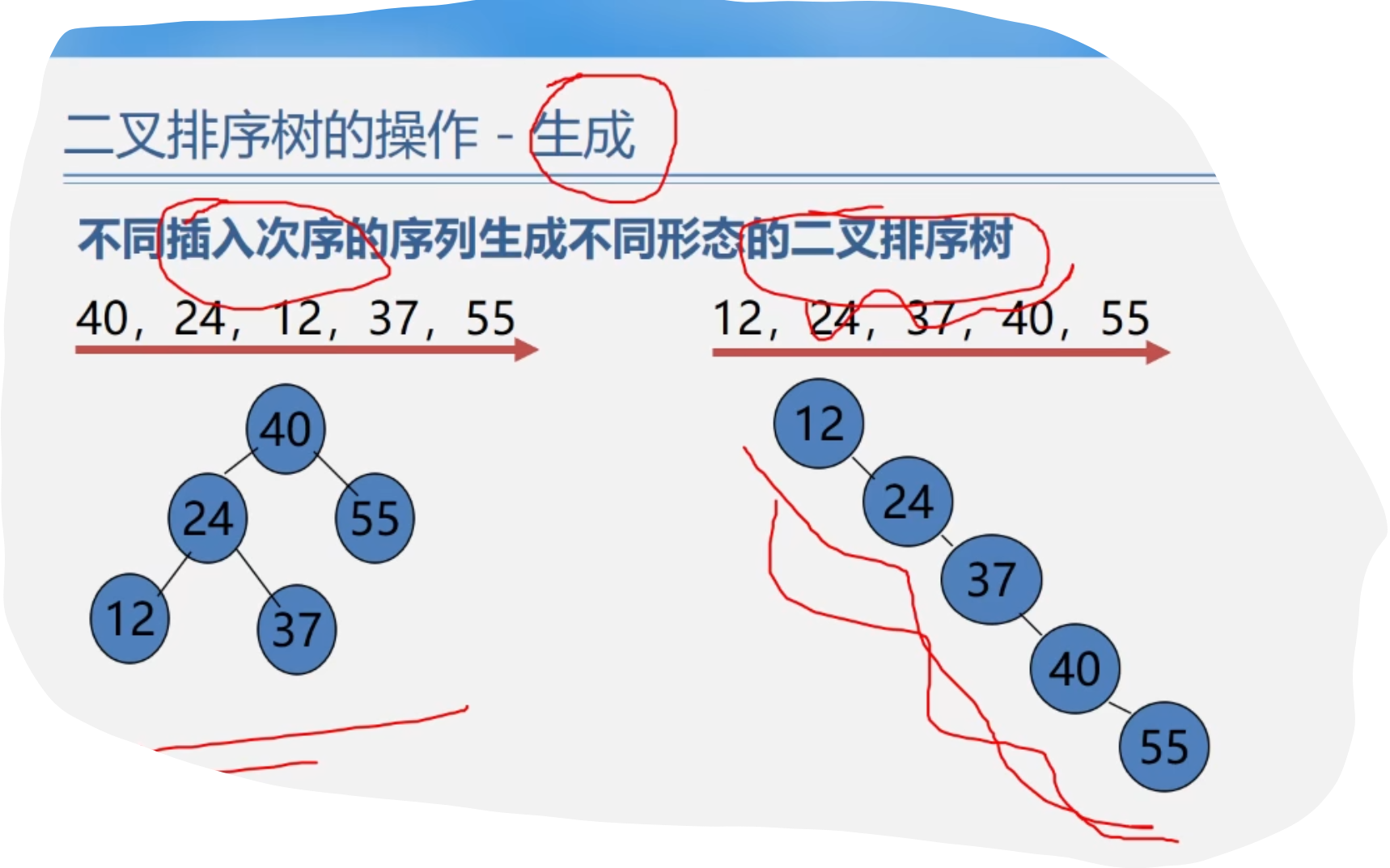
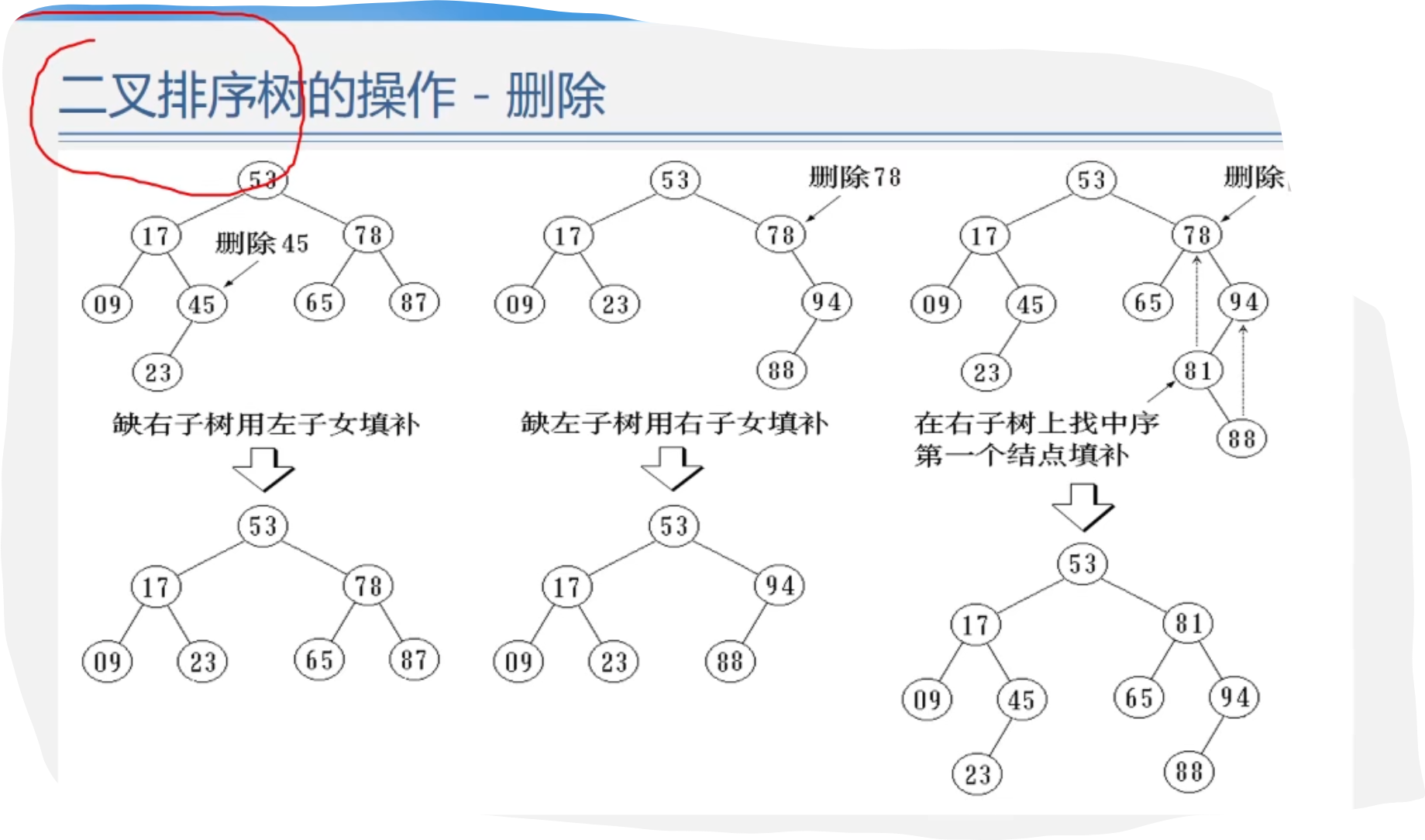
5.二叉排序树的操作-删除

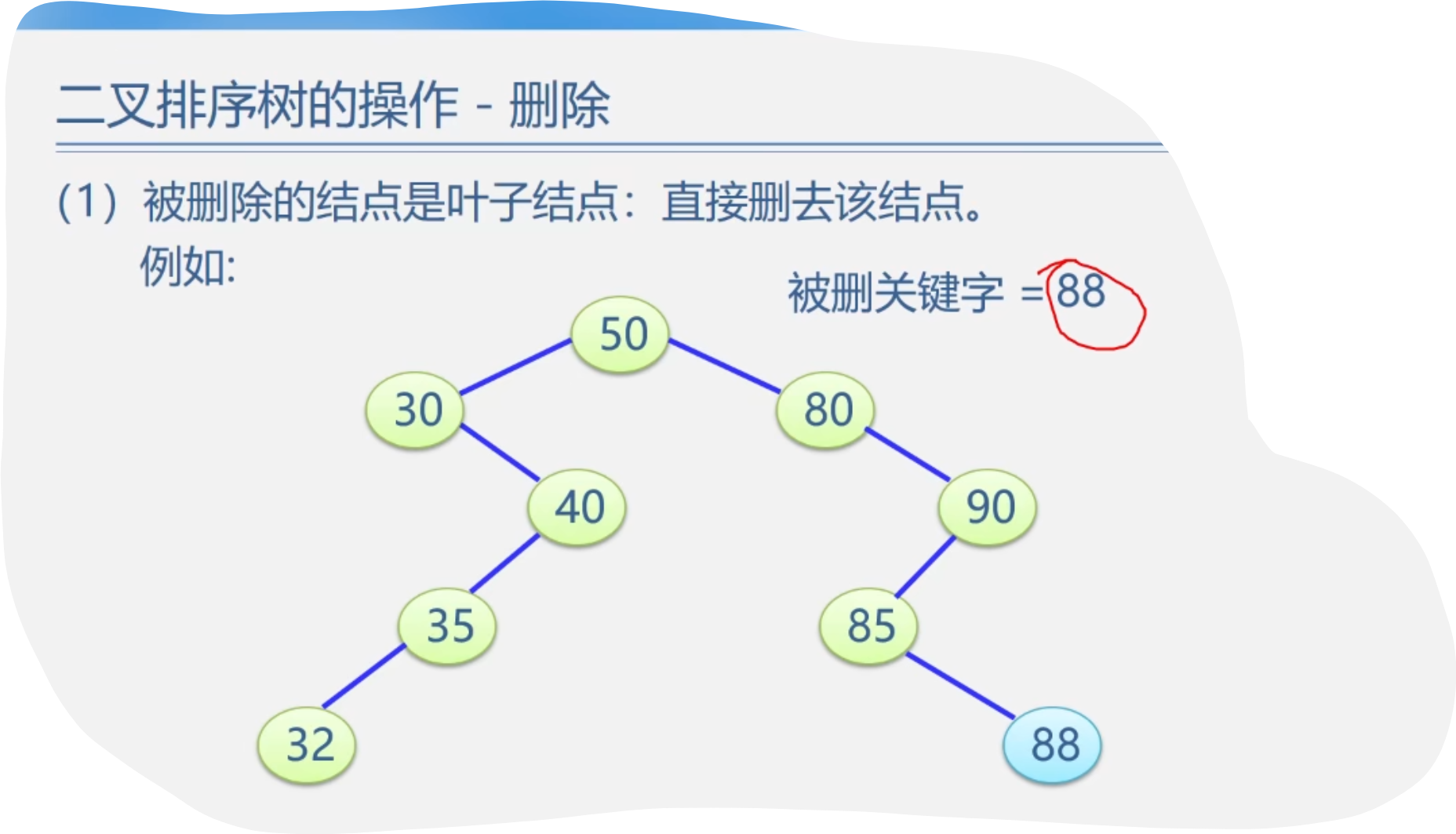
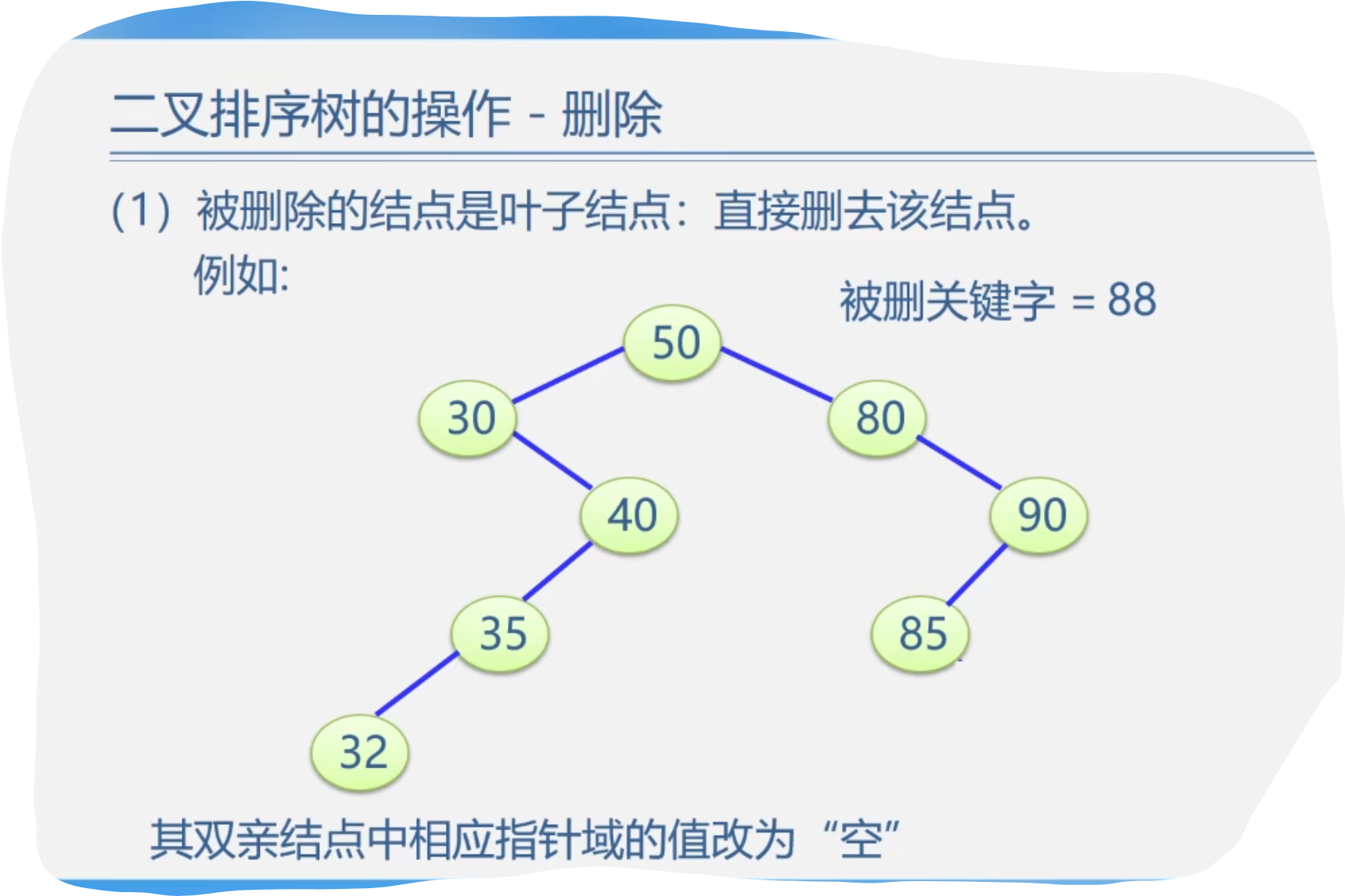
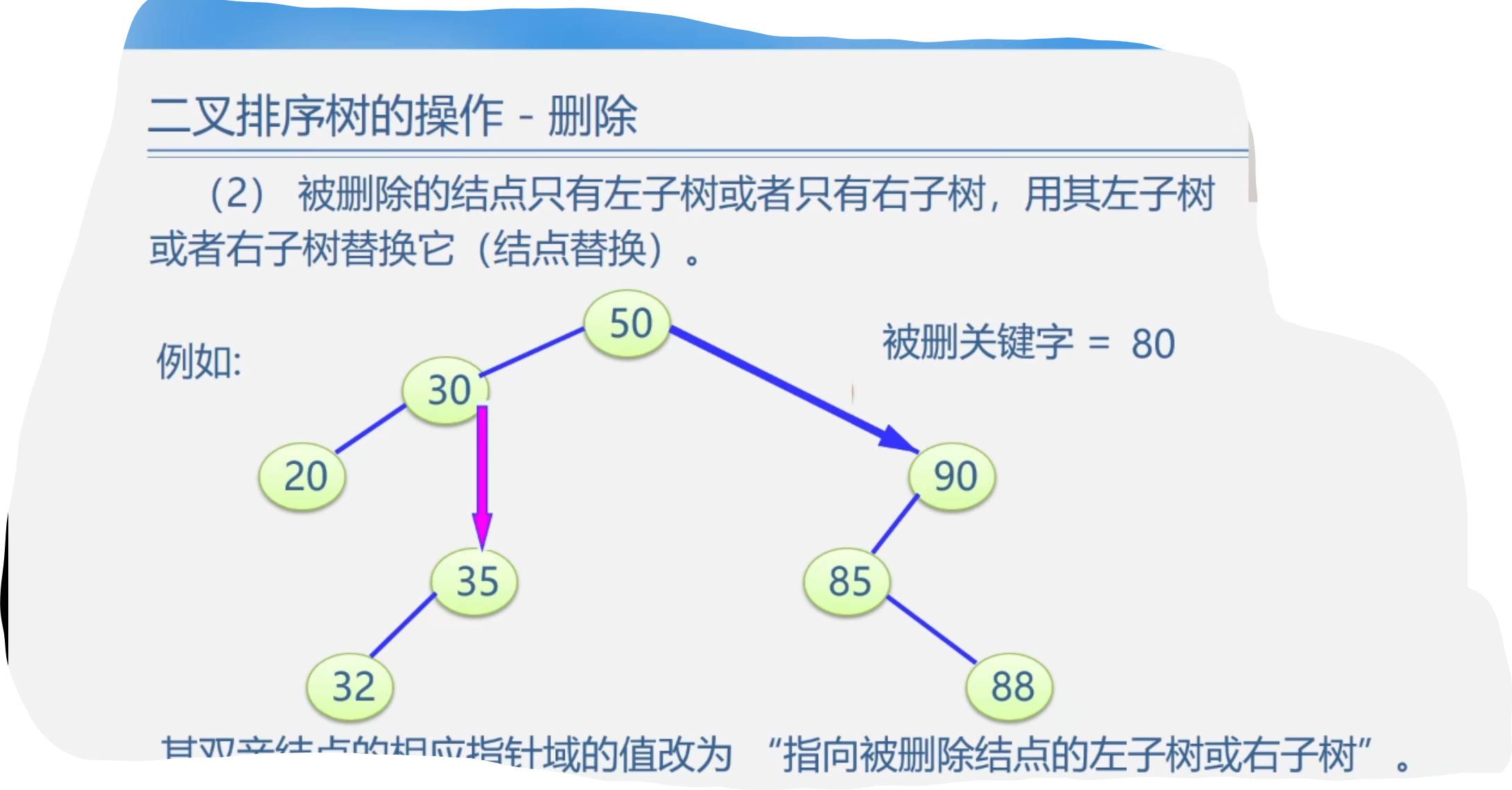
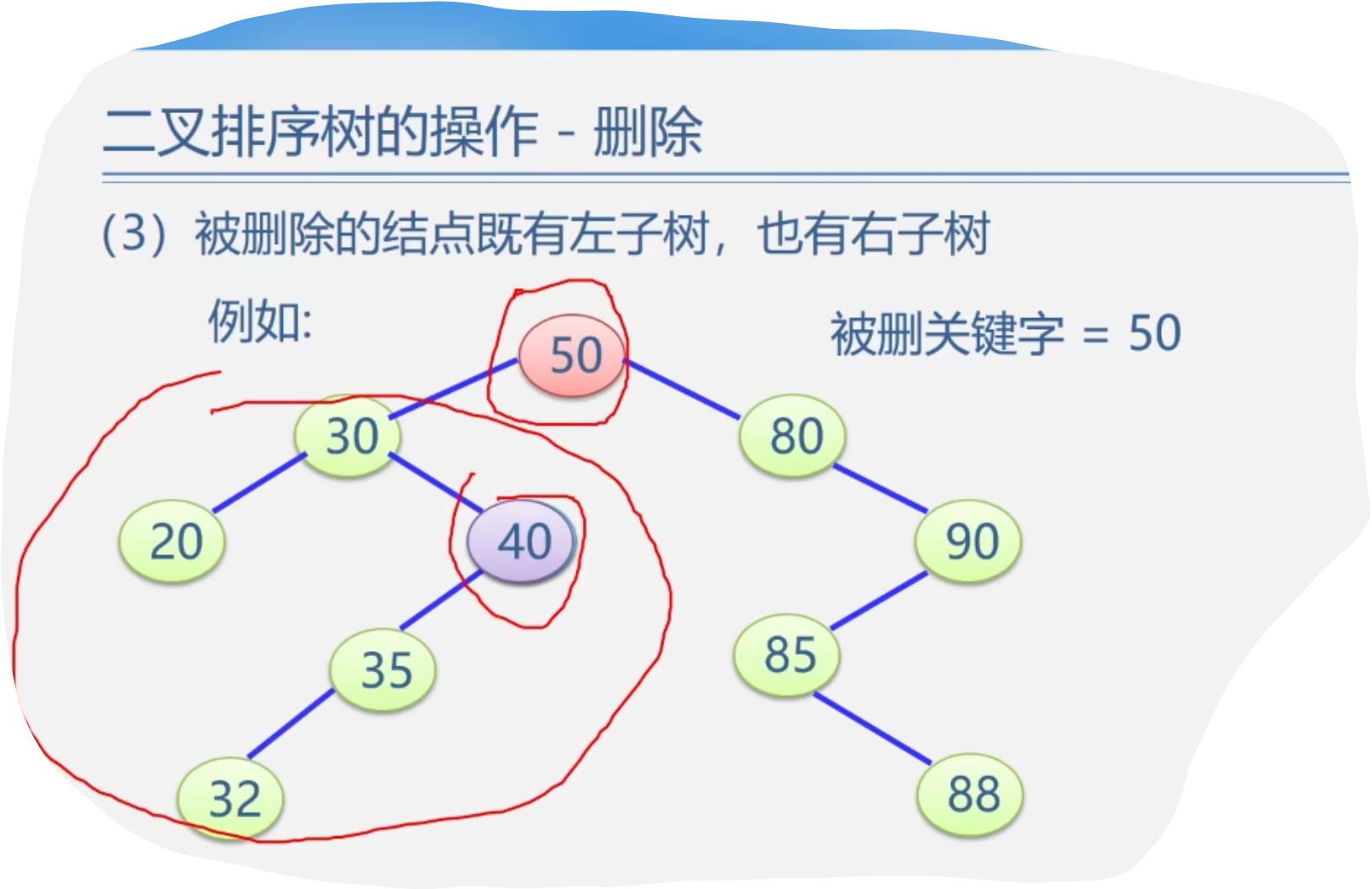
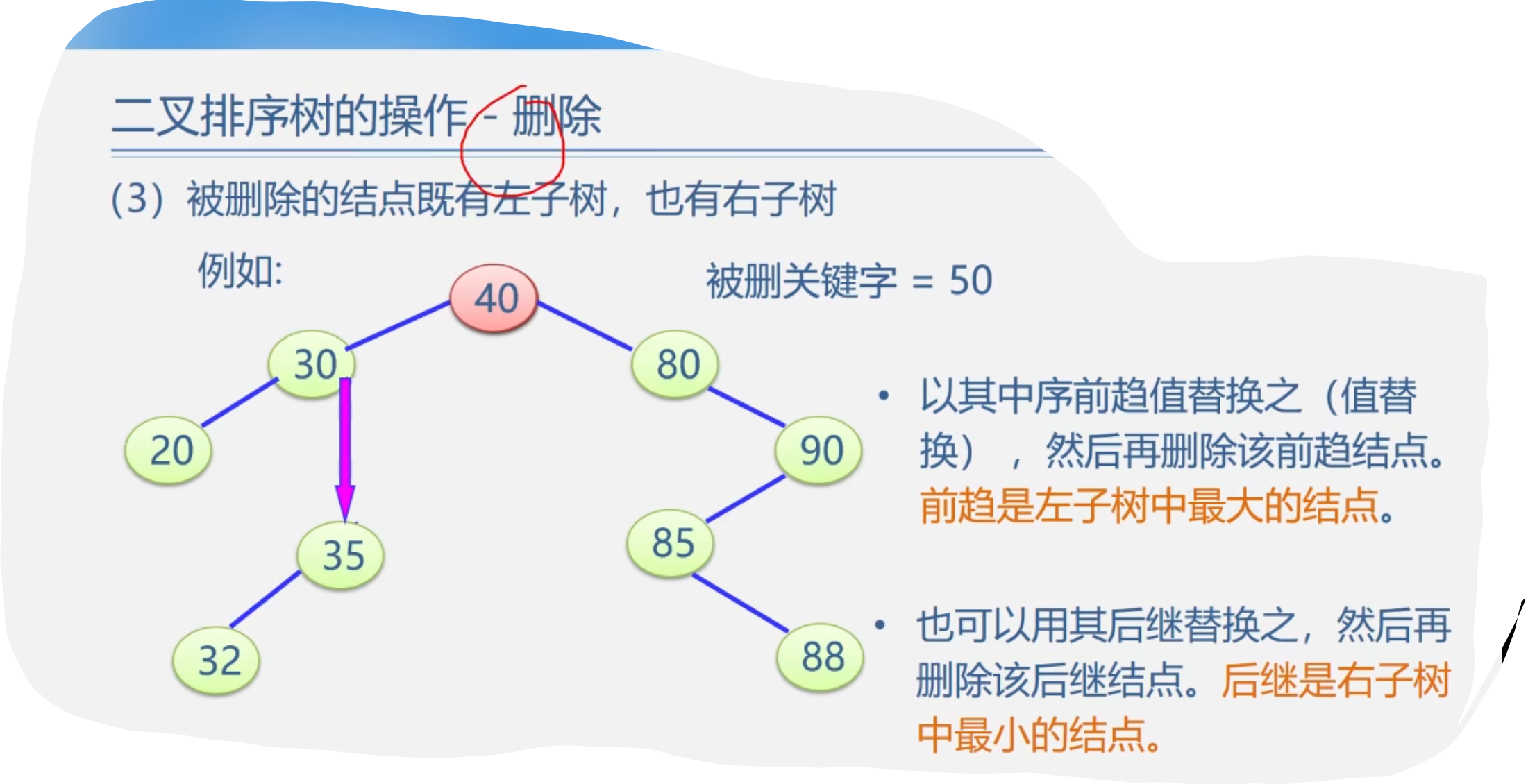
4.总的代码
#include<bits/stdc++.h> using namespace std; typedef struct { int key; }elem; typedef struct { elem *r; int len; }sstable; sstable st; int search_seq(sstable st,int key) { for(int i = st.len; i >= 1; --i) { if(st.r[i].key == key) return i; return 0; } } int Search_seq(sstable st,int key) { st.r[0].key = key; int i; for(i = st.len; st.r[i].key != key; --i); return i; } int search_bin(sstable st,int key) { int low = 1; int high = st.len; while(low <= high) { int mid = (low + high) / 2; if(st.r[mid].key == key) return mid; else if(key < st.r[mid].key) high = mid - 1; else low = mid + 1; } return 0; } typedef struct { int key; }elemtype; typedef struct bstnode { elemtype data; struct bstnode *lchild, *rchild; }bstnode,*bstree; bstree t; bstree searchbst(bstree t,int key) { if((!t) || key == t -> data.key) return t; else if(key < t -> data.key) return searchbst(t -> lchild,key); else return searchbst(t -> rchild,key); } int main() { return 0; }