目录
110. 平衡二叉树
题目描述
给定一个二叉树,判断它是否是平衡二叉树
平衡二叉树 是指该树所有节点的左右子树的深度相差不超过 1。
示例 1:
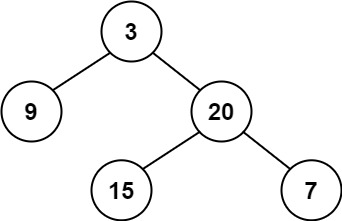
输入:root = [3,9,20,null,null,15,7] 输出:true 示例 2:
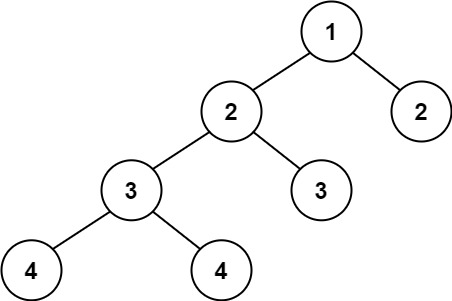
输入:root = [1,2,2,3,3,null,null,4,4] 输出:false 示例 3:
输入:root = [] 输出:true 提示:
- 树中的节点数在范围
[0, 5000]内 -104 <= Node.val <= 104
题解
显然,一个二叉树是平衡的,当且仅当它的所有子树都是平衡的。听起来就很适合递归秒了:
int getDepth(TreeNode *root) { if (!root) return 0; return max(getDepth(root->left), getDepth(root->right)) + 1; } bool isBalanced(TreeNode *root) { if (!root) return true; // 空树是平衡树 return abs(getDepth(root->left) - getDepth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right); } 相应地,考虑一下迭代法。由于需要判断各节点“左右子树的深度差”是否大于1,联想到基于后序遍历实现本题:因为后序遍历处理某一节点时,总是已经访问过其左右子树节点了。
// 基于层序遍历获取某个节点的深度 int getDepth(TreeNode *root) { if (!root) return 0; queue<TreeNode *> q; q.push(root); int depth = 0; while (!q.empty()) { int size = q.size(); for (int i = 0; i < size; i++) { if (q.front()->left) q.push(q.front()->left); if (q.front()->right) q.push(q.front()->right); q.pop(); } depth++; } return depth; } // 基于后序遍历检验平衡树 bool isBalanced(TreeNode *root) { if (!root) return true; // 统一迭代法的后序遍历 stack<TreeNode *> st; st.push(root); while (!st.empty()) { TreeNode *cur = st.top(); st.pop(); if (cur) { st.push(cur); // 中 st.push(nullptr); // 空节点标记 if (cur->left) st.push(cur->left); // 左 if (cur->right) st.push(cur->right); // 右 } else { if (abs(getDepth_II(st.top()->left) - getDepth_II(st.top()->right)) > 1) return false; st.pop(); } } return true; } 257. 二叉树的所有路径
题目描述
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
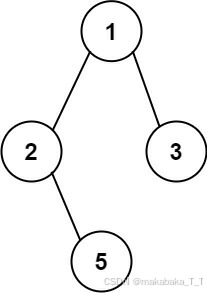
输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"] 示例 2:
输入:root = [1] 输出:["1"] 提示:
- 树中节点的数目在范围
[1, 100]内 -100 <= Node.val <= 100
题解
首先考虑递归解法,有两种,一是传统的DFS(深度优先搜索):
void getPathDFS(TreeNode *root, string path, vector<string> &res) { if (root) { path += to_string(root->val); // 递归出口:遍历到叶子节点 if (!root->left && !root->right) res.push_back(path); else { path += "->"; getPathDFS(root->left, path, res); getPathDFS(root->right, path, res); } } } vector<string> binaryTreePaths(TreeNode *root) { vector<string> res; getPathDFS(root, "", res); return res; } 二是结合回溯法,在基于递归的前序遍历框架下实现:
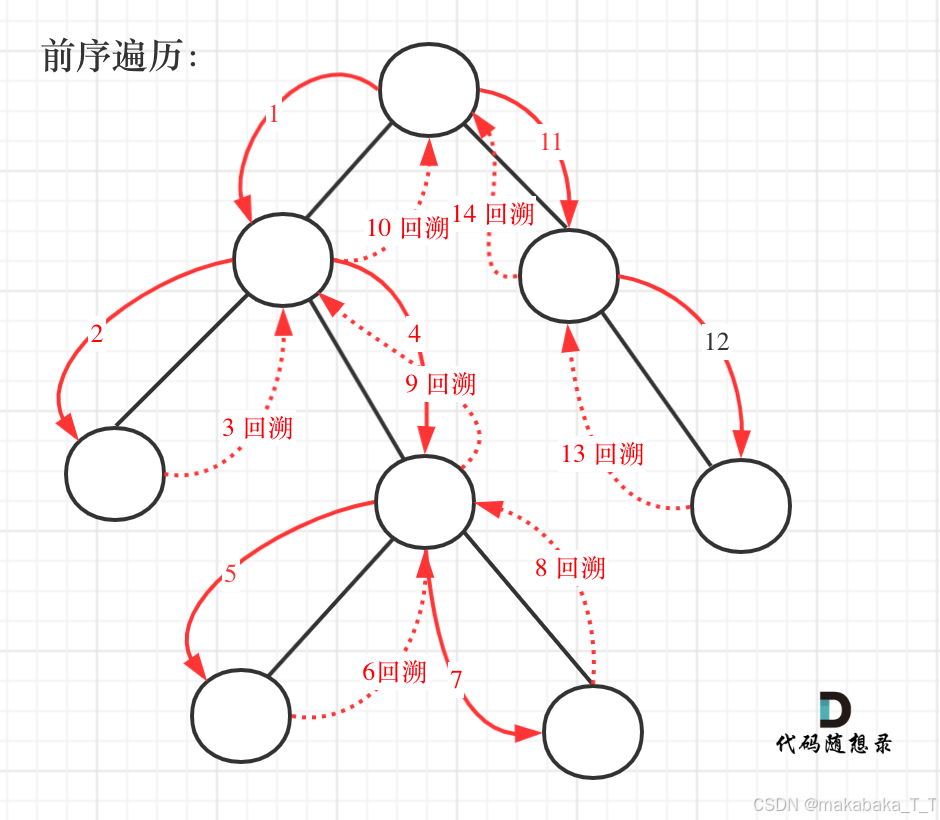
void traversal(TreeNode *root, vector<int> &paths, vector<string> &res) { // 由于需要找到所有路径,采用前序遍历实现 paths.push_back(root->val); // 中 // 递归出口:遍历到叶子节点 if (!root->left && !root->right) { string path = to_string(paths[0]); for (int i = 1; i < paths.size(); ++i) path += "->" + to_string(paths[i]); res.push_back(path); return; } if (root->left) { traversal(root->left, paths, res); // 左 paths.pop_back(); // 回溯 } if (root->right) { traversal(root->right, paths, res); // 右 paths.pop_back(); // 回溯 } } vector<string> binaryTreePaths(TreeNode *root) { vector<string> res; // 最终的结果集 vector<int> paths; // 存储每条路径的数组(按照路径上节点的值) if (!root) return res; traversal(root, paths, res); return res; } 其中每次回溯的作用相当于回退到上一个“分支点”,再选择一条与之前不同的分支进行操作,原理可以参考 代码随想录本题讲解 中的这张图,从始至终走一遍应该就能领会了:
最后还是考虑一下迭代法,同上面一样,要基于前序遍历的框架实现,具体来说就是在 统一迭代法 的基础上,新建一个存储当前路径的栈,随着“右左中”节点的入栈,相应的路径也要更新、入栈:
vector<string> binaryTreePaths(TreeNode *root) { // 基于前序遍历的统一迭代法实现 vector<string> res; stack<string> pathSt; stack<TreeNode *> nodeSt; if (!root) return res; nodeSt.push(root); pathSt.push(to_string(root->val)); while (!nodeSt.empty()) { TreeNode *node = nodeSt.top(); nodeSt.pop(); string path = pathSt.top(); pathSt.pop(); if (node) { if (node->right) { pathSt.push(path + "->" + to_string(node->right->val)); nodeSt.push(node->right); // 右 } if (node->left) { pathSt.push(path + "->" + to_string(node->left->val)); nodeSt.push(node->left); // 左 } nodeSt.push(node); // 中 nodeSt.push(nullptr); // 空节点标记 pathSt.push(path); // 记录当前路径 } else { if (!nodeSt.top()->left && !nodeSt.top()->right) res.push_back(path); // 已到叶子节点:当前路径加入结果集 nodeSt.pop(); } } return res; } ⚠️ 值得注意的是,为了保证每次路径栈顶的路径与节点栈顶的节点“一一对应”,两个栈要同步操作(一起 push 和 pop 。唯一例外的是最后路径加入结果集时,节点栈 pop 了但是路径栈没有:
... else { if (!nodeSt.top()->left && !nodeSt.top()->right) res.push_back(path); // 已到叶子节点:当前路径加入结果集 nodeSt.pop(); } 这是因为在每次循环一开始,两个栈就已经同时 pop 过了:
while (!nodeSt.empty()) { TreeNode *node = nodeSt.top(); nodeSt.pop(); string path = pathSt.top(); pathSt.pop(); ... 而若要进入 else 、记录结果,上面这里节点栈弹出的是标记用的空节点,所以它自己最后还要再 pop 一次来弹出真正的节点,而路径栈就不用了。
404. 左叶子之和
题目描述
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
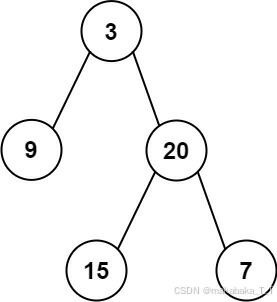
输入: root = [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24 示例 2:
输入: root = [1] 输出: 0 提示:
- 节点数在
[1, 1000]范围内 -1000 <= Node.val <= 1000
题解
比较简单,还是可以递归和迭代实现。要注意的就是判断左叶子只能通过其父节点判断:
root->left && !root->left->left && !root->left->right 即父节点有左孩子、且这个左孩子无左右孩子,则这个左孩子是左叶子。
递归法
int sumOfLeftLeaves(TreeNode *root) { // 递归出口1:当前节点为空 if (!root) return 0; int leftSum = sumOfLeftLeaves(root->left); // 递归出口2:当前节点的左孩子是左叶子 if (root->left && !root->left->left && !root->left->right) leftSum = root->left->val; return leftSum + sumOfLeftLeaves(root->right); } 迭代法
int sumOfLeftLeaves_II(TreeNode *root) { if (!root) return 0; queue<TreeNode*> q; q.push(root); int sum = 0; while (!q.empty()) { int size = q.size(); for (int i = 0; i < size; ++i) { TreeNode *cur = q.front(); if (cur->left) { q.push(cur->left); if (!cur->left->left && !cur->left->right) sum += cur->left->val; } if (cur->right) q.push(cur->right); q.pop(); } } return sum; } 222. 完全二叉树的节点个数
题目描述
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
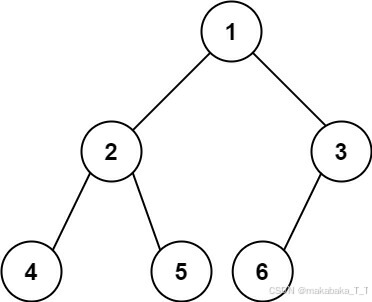
输入:root = [1,2,3,4,5,6] 输出:6 示例 2:
输入:root = [] 输出:0 示例 3:
输入:root = [1] 输出:1 提示:
- 树中节点的数目范围是
[0, 5 * 104] 0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
进阶: 遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
题解
无脑算法当然就是遍历整棵树,记录节点个数即可(这样应该直接层序遍历最方便),时间复杂度为 O ( n ) O(n) O(n) ,不赘述。
考虑利用完全二叉树的性质提升速度。根据其性质,完全二叉树的子树中有很多都是满二叉树,而一个 n n n 层满二叉树的节点个数为 2 n − 1 2^n - 1 2n−1 。所以我们可以利用这点,进行带剪枝的递归遍历:
- 以当前节点为根,所得子树为满二叉树,则按公式计算节点数
- 否则,递归计算节点数
其中,判断满二叉树的方法也很简单高效:看“最左”枝和“最右”枝的深度是否相同即可。
代码(C++)
int countNodes(TreeNode *root) { if (!root) return 0; TreeNode *left = root->left; TreeNode *right = root->right; int leftDepth = 0, rightDepth = 0; // 左、右子树深度 while (left) { left = left->left; leftDepth++; } while (right) { right = right->right; rightDepth++; } if (leftDepth == rightDepth) // 满二叉树,直接用公式计算 return (2 << leftDepth) - 1; return countNodes(root->left) + countNodes(root->right) + 1; } 这里用位运算,
2 << leftDepth相当于 2 l e f t D e p t h + 1 2^{leftDepth + 1} 2leftDepth+1 ,其中+1是因为leftDepth是子树深度,还要加上根节点的1才是相应的树深度 n n n 。
