阅读量:1
文章目录
121. 小红的区间翻转
小红拿到了两个长度为 n 的数组 a 和 b，她仅可以执行一次以下翻转操作：选择a数组中的一个区间[i, j]，（i != j)，将它们翻转。例如，对于 a = [2,3,4,1,5,6]，小红可以选择左闭右闭区间[2,4]，数组 a 则变成[2,3,5,1,4,6]。
小红希望操作后 a 数组和 b 数组完全相同。请你告诉小红有多少种操作的方案数。
初始 a 数组和 b 数组必定不相同。
输入描述
第一行输入一个正整数 n，代表数组的长度； 第二行输入 n 个正整数 ai； 第三行输入 n 个正整数 bi。 输出描述 选择区间的方案数。 输入示例
4 1 2 3 1 1 3 2 1 输出示例
2 提示信息
数据范围 1 ≤ n, ai ,bi ≤ 103 在示例中： 将 1 2 3 1 中的 2 3 进行翻转，得到 1 3 2 1。 将 1 2 3 1 整个进行翻转，得到 1 3 2 1。 所以最终结果是 2。 思路：考虑先找到满足条件的最大left索引和最小right索引，然后进行循环：每次循环left–，right++，如果说A[left]==B[right]，说明翻转后还是相同，直到两者不等，那么此时就可以break了。
import java.util.*; class Main{ public static void main(String[] args){ Scanner scanner = new Scanner(System.in); int len = scanner.nextInt(); int[] A = new int[len], B = new int[len]; for(int i = 0; i < len; i++){ A[i] = scanner.nextInt(); } for(int i = 0; i < len; i++){ B[i] = scanner.nextInt(); } System.out.println(cal(A, B, len)); } private static int cal(int[] A, int[] B, int len){ int start = 0, end = len - 1; //定位到A与B第一个不相同的地方，这个时候需要考虑进行翻转了 while(A[start] == B[start]){ start++; } while(A[end] == B[end]){ end--; } //找到满足条件的最大left索引和最小right索引 int left = start, right = end; while(left <= end && right >= start){ if(A[left] != B[right]) return 0; left++; right--; } int res = 1; int l = start - 1, r = end + 1; //进行循环 while(l >= 0 && r < len){ if(A[l] != B[r]){ break; }else{ res++; } l--; r++; } return res; } } 142. 两个字符串的最小 ASCII 删除总和
题目描述
给定两个字符串 s1 和 s2（0 <= s1.length, s2.length <= 1000），返回使两个字符用相等所需删除字符的 ASCLL 值的最小和。 s1 和 s2 由小写英文字母组成。 输入描述
输入共两行，每行一个字符串。 输出描述
输出一个正整数，表示使两个字符用相等所需删除字符的 ASCLL 值的最小和。 输入示例
sea eat 输出示例
231 提示信息
解释:在“sea”中删除“s”并将"s”的值(115)加入总和。 在"eat”中删除“t“并将116 加入总和。 结束时，两个字符串相等，115+116 =231 就是符合条件的很小和。 思路：动态规划：记 d p [ i ] [ j ] dp[i][j] dp[i][j]为str1到str2最小 ASCII 删除总和，于是有转移方程
d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] , i f s t r 1 [ i − 1 ] = = s t r 2 [ j − 1 ] d p [ i ] [ j ] = m i n ( d p [ i − 1 ] [ j ] + s t r 1 ( i − 1 ) , d p [ i ] [ j − 1 ] + s t r 2 ( j − 1 ) ) dp[i][j]=dp[i-1][j-1],\quad if\quad str1[i-1]==str2[j-1] \\ dp[i][j] =min(dp[i-1][j]+str1(i-1),dp[i][j-1]+str2(j-1)) dp[i][j]=dp[i−1][j−1],ifstr1[i−1]==str2[j−1]dp[i][j]=min(dp[i−1][j]+str1(i−1),dp[i][j−1]+str2(j−1))
还有边界条件
d p [ 0 ] [ 0 ] = 0 d p [ i ] [ 0 ] = d p [ i − 1 ] [ 0 ] + s t r 1 ( i − 1 ) d p [ 0 ] [ j ] = d p [ 0 ] [ j − 1 ] + s t r 2 ( j − 1 ) dp[0][0]=0 dp[i][0]=dp[i-1][0]+str1(i-1)\\ dp[0][j]=dp[0][j-1]+str2(j-1) dp[0][0]=0dp[i][0]=dp[i−1][0]+str1(i−1)dp[0][j]=dp[0][j−1]+str2(j−1)
然后空间优化方面，由于 d p [ i ] [ j ] dp[i][j] dp[i][j]只与 d p [ i − 1 ] [ j ] ， d p [ i ] [ j − 1 ] ， d p [ i − 1 ] [ j − 1 ] dp[i-1][j]，dp[i][j-1]，dp[i-1][j-1] dp[i−1][j]，dp[i][j−1]，dp[i−1][j−1]有关，所以可以优化成一维数组。
d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]就是 d p [ j ] dp[j] dp[j]
d p [ i ] [ j ] dp[i][j] dp[i][j]就是 d p [ j ] dp[j] dp[j]
d p [ i ] [ j − 1 ] dp[i][j-1] dp[i][j−1]就是 d p [ j − 1 ] dp[j-1] dp[j−1]
而 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]就需要先利用 p r e v prev prev记录 d p [ i − 1 ] [ 0 ] dp[i-1][0] dp[i−1][0]，再在内层循环时用 t e m p temp temp记录 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]
import java.util.*; class Main{ public static void main (String[] args) { Scanner scanner = new Scanner(System.in); String str1 = scanner.next(); String str2 = scanner.next(); System.out.println(AsciiSum(str1, str2)); } private static int AsciiSum(String str1, String str2){ int m = str1.length(); int n = str2.length(); int[] dp = new int[n + 1]; for(int j = 1; j <= n; j++){ dp[j] = dp[j - 1] + str2.charAt(j - 1); } for(int i = 1; i <= m; i++){ int prev = dp[0]; dp[0] += str1.charAt(i - 1); for(int j = 1; j <= n; j++){ int temp = dp[j]; if(str1.charAt(i - 1) == str2.charAt(j - 1)){ dp[j] = prev; }else{ dp[j] = Math.min(dp[j] + str1.charAt(i-1),dp[j-1]+str2.charAt(j-1)); } prev = temp; } } return dp[n]; } } 143. 最长同值路径
题目描述
给定一个二叉树的 root ，返回最长的路径的长度，这个路径中的每节点具有相同值。 这条路径可以经过也可以不经过根节点。两个节点之间的路径长度 由它们之间的边数表示。 树的节点数的范围是 [0,10^4] -1000 <= Node.val <= 1000 树的深度将不超过 18 层 输入描述
输入共两行，第一行是一个整数 n，表示第二行的字符串数。 第二行包含 n 个字符串，空格隔开，数字的字符串代表该节点存在，并且值为数字，null 代表是一个空结点。 输出描述
输出一个正整数，代表最长路径长度。 输入示例
7 5 4 5 1 1 null 5 输出示例
2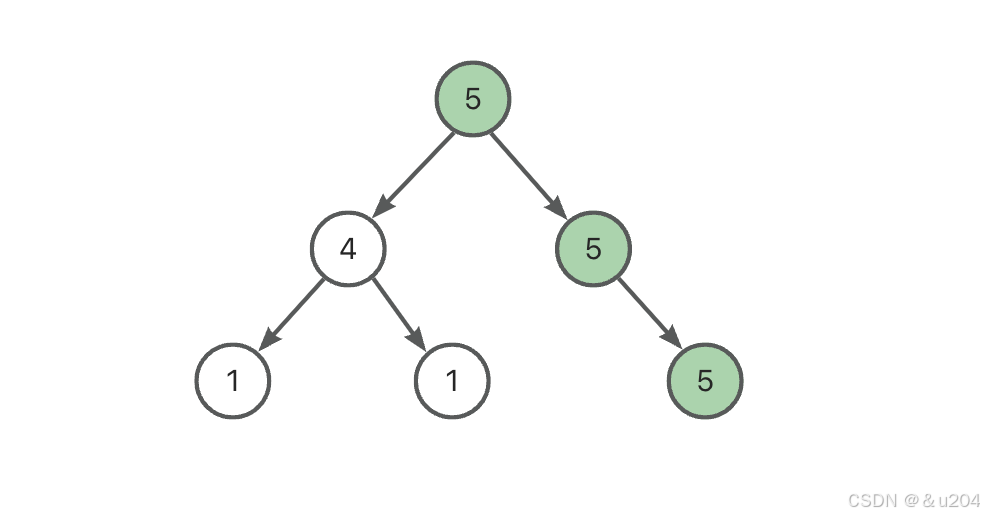 
这题有两个难点，第一个自然就是找到最长路径长度，但另一个难点是如何构造需要的二叉树，所以这个问题可以拆成两个部分：
- 根据输入构建二叉树
- 根据二叉树找到最长路径长度
上面两点分别对应了deSerialize方法和dfs方法，两个方法本身并不算复杂，只不过需要熟练掌握队列的使用。
import java.util.*; class Main{ static int max; public static void main (String[] args) { max = 0; Scanner sc = new Scanner(System.in); int n = sc.nextInt(); sc.nextLine(); String str = sc.nextLine(); TreeNode root = deSerialize(str); dfs(root); System.out.println(max); } private static int dfs(TreeNode node){ if(node == null) return 0; int cur = 0, res = 0, left = dfs(node.left), right = dfs(node.right); int left1 = 0, right1 = 0; if(node.left != null && node.val == node.left.val){ left1 = left + 1; } if(node.right != null && node.val == node.right.val){ right1 = right + 1; } max = Math.max(max, left1 + right1); return Math.max(left1, right1); } private static TreeNode deSerialize(String s){ String[] vals = s.split(" "); TreeNode root = new TreeNode(Integer.parseInt(vals[0])); Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); int i = 1; while(!queue.isEmpty()){ TreeNode node = queue.poll(); if(i < vals.length && !vals[i].equals("null")){ node.left = new TreeNode(Integer.parseInt(vals[i])); queue.offer(node.left); } i++; if(i < vals.length && !vals[i].equals("null")){ node.right = new TreeNode(Integer.parseInt(vals[i])); queue.offer(node.right); } i++; } return root; } } class TreeNode{ TreeNode left; TreeNode right; int val; TreeNode(){} TreeNode(int val){ this.val = val; } } 139.完美数
题目描述
小红定义一个数为“完美数”，当且仅当该数仅有一个非零数字。例如 5000, 4, 1, 10, 200 都是完美数。 小红拿到了一个大小为 n（2 <= n <= 2000）的数组 a，她希望选择数组中的两个元素（1 <= a[i] <= 10^9），满足它们的乘积为完美数。 小红想知道，共有多少种不同的取法? 输入描述
第一行输入一个整数 n，表示数组大小。 第二行输入 n 个整数，整数之间用空格隔开，表示数组中的元素。 输出描述
输出一个整数，表示取法个数。 输入示例
4 25 2 1 16 输出示例
3 提示信息
25 * 2 = 50； 2 * 1 = 2； 25 * 16 = 400。 难度不大，将long来存储乘积结果并用String来进行0的判断是关键。
import java.util.*; class Main{ public static void main (String[] args) { Scanner sc = new Scanner(System.in); int res = 0; int n = sc.nextInt(); long[] nums = new long[n]; for(int i = 0; i < n; i++){ nums[i] = sc.nextInt(); } for(int i = 0; i < n; i++){ for(int j = i + 1; j < n; j++){ long ans = nums[i] * nums[j]; if(isValid(ans)) res++; } } System.out.println(res); } private static boolean isValid(long ans){ String s = String.valueOf(ans); for(int i = 1; i < s.length(); i++){ if(s.charAt(i) != '0'){ return false; } } return true; } } 140. 可爱串
题目描述
我们定义子序列为字符串中可以不连续的一段，而子串则必须连续。 例如 rderd 包含子序列 "red”，且不包含子串"red”，因此该字符串为可爱串。 小红想知道，长度为 n（3 <= n <= 10 ^ 5）的、仅由 'r''e''d' 三种字母组成的字符串中，有多少是可爱串? 答案请对 10 ^ 9 + 7 取模。 输入描述
输入共一行，包含一个正整数 n 输出描述
输出一个正整数，代表可爱串的数量 输入示例
4 输出示例
3 提示信息
"reed"、"rerd"、"rded" import java.util.*; public class Main{ static long MOD = (long) (1e9 + 7); public static void main(String[] args) { Scanner in = new Scanner(System.in); int n = in.nextInt(); long[] dp1 = new long[n + 1]; long[] dp2 = new long[n + 1]; long[] dp3 = new long[n + 1]; // 可爱串的个数 = 包含“red”子序列的方案个数 - 包含“red”子串的方案个数 // dp1[i]表示长度为i的包含“red”子串的方案个数 for (int i = 3; i <= n; i++) { dp1[i] = (3 * dp1[i - 1] + pow(3,i - 3) - dp1[i - 3] + MOD) % MOD; } // dp2[i]表示长度为i的包含“re”子序列的方案个数 for (int i = 2; i <= n; i++) { dp2[i] = ((2 * dp2[i - 1]) + (i - 1) * pow(2, i - 2) + MOD) % MOD; } // dp3[i]表示长度为i的包含“red”子序列的方案个数 for (int i = 3; i <= n; i++) { dp3[i] = (3 * dp3[i - 1] + dp2[i - 1] + MOD) % MOD; } System.out.println(dp3[n] - dp1[n]); } private static long pow(long x, long n) { long res = 1; while (n > 0) { if ((n & 1) == 1) { // 如果 n 是奇数 res = res * x % MOD; } x = x * x % MOD; n >>= 1; // n 右移一位，相当于除以 2 } return res; } } 141. 好二叉树
题目描述
小红定义一个二叉树为“好二叉树”，当且仅当该二叉树所有节点的孩子数量为偶数(0 或者 2)。 小红想知道，n（1<= n <=3000）个节点组成的好二叉树，共有多少种不同的形态? 答案请对 10 ^ 9 + 7 取模。 输入描述
输入一个正整数 n 输出描述
输出一个正整数，代表好二叉树的数量 输入示例
5 输出示例
2 思路：动态规划，一个二叉树除了根节点可以分为左子树和右子树，设分别有 j j j个和 k − j k-j k−j个，其中 k = i − 1 k=i-1 k=i−1， j j j遍历每一个奇数即可。
import java.util.*; class Main{ static long MOD = (long)(1e9 + 7); public static void main (String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); long[] dp = new long[3001]; dp[1] = dp[3] = 1; for(int i = 5; i <= n; i += 2){ for(int j = 1, k = i - 1; j < k; j += 2){ dp[i] += (dp[j] * dp[k-j]) % MOD; dp[i] %= MOD; } } System.out.println(dp[n]); } } 