阅读量:4
快速排序 - go
一、思路
快速排序是一种分治策略的排序算法,关键过程是对数组进行划分。选择一个基准值(pivot element),围绕着这个基准值划分子数组,对子数组递归调用快速排序,直到数组有序。
二、步骤及图解
1、选取基准元素。将最后一个元素(随机值、三数中值) 作为基准值 pivot。
2、划分子数组。遍历数组,将小于基准值的元素交换到左边,大于基准值的元素交换到右边,将基准值交换到正确的位置,并返回其索引作为分区点。经过这一步骤之后,数组被划分成小于和大于基准值的2个子数组。
3、递归调用。递归地对这2个子数组进行快速排序,直到整个数组有序。
- 一次快速排序的过程
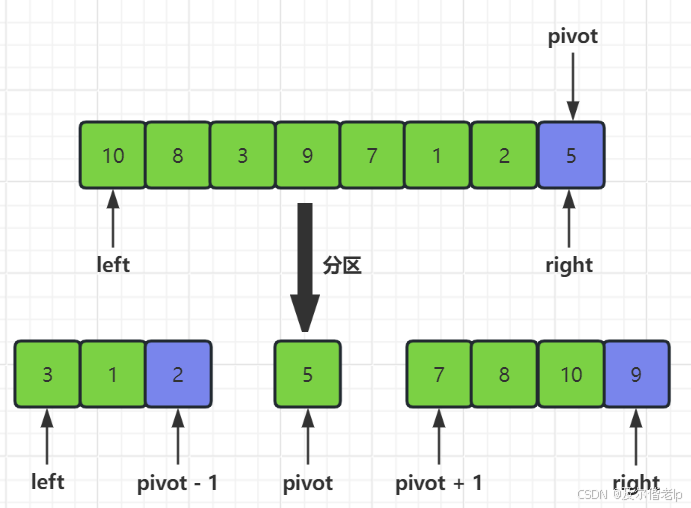
- 快速排序全过程
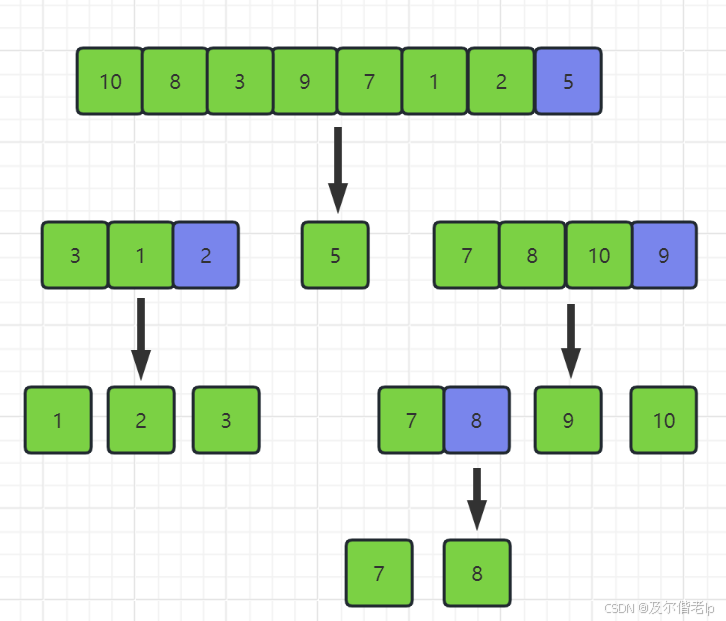
- 数组变化
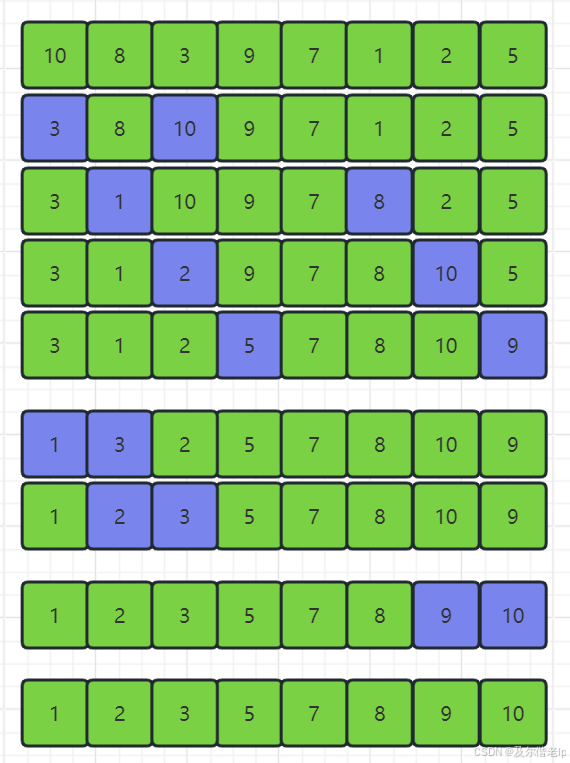
三、代码实现
package main import "fmt" func main() { arr := []int{10, 8, 3, 9, 7, 1, 2, 5} quickSort(arr, 0, len(arr)-1) fmt.Println("Sorted array:", arr) // Sorted array: [1 2 3 5 7 8 9 10] } // left,right分别为数组的最左、最右下标 func quickSort(arr []int, left, right int) { if left >= right { // 递归截止条件 return } pivot := partition(arr, left, right) quickSort(arr, left, pivot-1) quickSort(arr, pivot+1, right) } // 分区函数 func partition(arr []int, left, right int) int { pivot := arr[right] // 选择数组的最后一个元素作为基准值 i := left // 数组最左元素的下标 for j := left; j < right; j++ { if arr[j] < pivot { // 将小于基准值的元素交换到左边 arr[i], arr[j] = arr[j], arr[i] i++ } } // 处理基准值 arr[i], arr[right] = arr[right], arr[i] return i } // 空间复杂度:O(1), 在分区时使用原地交换的方式 四、复杂度分析
- 时间复杂度:O(n log n)
快速排序的时间复杂度可以通过递归树来分析。在每一层中,我们选择一个主元素并将数组划分为两个子数组,时间复杂度为O(n)。如果我们将递归树表示为二叉树,则总共有 log n 层,并且每层的时间复杂度为 O(n),因此整个算法的时间复杂度为 O(n log n)。
以下情况快速排序的时间复杂度将退化为 O(n^2):
1、数组已经有序。在待排序数组已经有序的情况下,每次划分只能减少一个元素,时间复杂度将退化为 O(n^2)。
2、基准值有问题。选择的基准值不能把数组分区成均衡的两部分,基准值都是最小或最大的元素,导致每次分区后,一个子数组为空,而另一个子数组包含剩余的所有元素,时间复杂度将退化为O(n^2)。
- 空间复杂度:O(log n)
快速排序的空间复杂度主要由递归调用栈决定。在最好的情况下(即每次分区都非常平衡),递归深度为 log n,因此空间复杂度为 O(log n)。
在最坏的情况下(即每次分区都极度不平衡),递归深度可以达到 n,空间复杂度将退化为 O(n)。
快速排序是不稳定的排序算法,因为在排序过程中会涉及到交换操作,可能导致相同元素的相对顺序发生变化。
然而,有时候也可以通过一些技巧使得快排变成稳定排序。例如,在选择主元素时,可以选择第一个或最后一个元素,这样就可以避免在分区过程中出现相同元素的前后位置发生变化的情况。
