目录


专栏:数学建模学习笔记
1. 问题背景和描述
1.1 问题背景
在现代制造业和商业运作中,资源的有效利用和利润的最大化是企业追求的重要目标。企业面临的常见问题是如何在有限的资源条件下,通过合理分配和优化使用资源,来实现利润的最大化。线性规划(Linear Programming,LP)是一种数学优化技术,能够在这些情况下发挥重要作用。它通过建立数学模型,帮助企业在众多可能的选择中找到最优解,进而指导实际操作。
假设有一家工厂,生产两种产品:产品A和产品B。每种产品的生产都需要消耗特定的资源。每天,每种资源的使用时间是有限的,这使得资源分配问题变得复杂。工厂的目标是通过合理分配资源,确定每天应该生产多少单位的产品A和产品B,以实现总利润的最大化。
具体数据如下:
- 资源1:每天最多可用60个小时
- 资源2:每天最多可用40个小时
- 产品A:每单位需要资源1的2个小时和资源2的1个小时
- 产品B:每单位需要资源1的1个小时和资源2的2个小时
- 产品A:每单位的利润为30美元
- 产品B:每单位的利润为20美元
通过对这些数据进行分析和建模,我们可以利用线性规划技术来制定一个优化的生产计划,确保在资源限制条件下实现利润的最大化。
1.2 问题描述
我们需要建立一个线性规划模型来描述上述问题,并使用该模型找到每天应该生产的产品A和产品B的最优数量,从而实现总利润的最大化。同时,生产过程中必须满足资源的限制条件,即不能超过每天可用的资源时间。
在这个问题中,我们的目标是构建一个数学模型,通过这个模型可以:
- 确定每天生产的产品A和产品B的数量。
- 满足资源的限制条件。
- 实现总利润的最大化。
2. 数学模型的建立
建立数学模型是解决线性规划问题的基础。我们将根据问题背景中的具体数据,定义决策变量,构建目标函数和约束条件。
2.1决策变量
决策变量是我们希望通过优化确定的数量。在这个问题中,决策变量是每天生产的产品A和产品B的数量。我们定义两个决策变量:
- x1:每天生产的产品A的单位数量
- x2:每天生产的产品B的单位数量
这些决策变量将用于构建目标函数和约束条件。
2.2 目标函数
目标函数是我们希望优化的表达式。在这个问题中,目标是最大化总利润。总利润可以表示为生产的产品A和产品B的利润之和。具体来说:
- 产品A每单位的利润为30美元
- 产品B每单位的利润为20美元
因此,总利润可以表示为: 利润=30x1+20x2
我们的目标是最大化总利润,因此目标函数可以表示为: 最大化 z=30x1+20x2
2.3 约束条件
约束条件是模型中必须满足的限制。在这个问题中,约束条件包括资源的限制和生产数量的非负性。
资源1的限制: 2*x1+x2≤60
资源2的限制:x1+2*x2≤40
非负约束:x1≥0 ,x2≥0
这些约束条件确保生产计划不会超过可用的资源,并且生产的数量是非负的,即实际可行的。
2.4 数学模型总结
综合以上信息,我们可以建立一个完整的线性规划模型来描述这个问题。模型的形式如下:
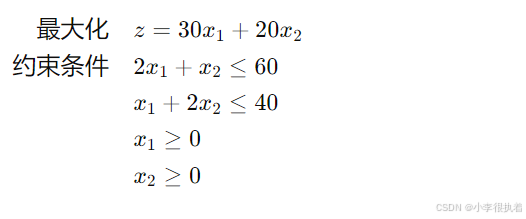
3. 使用Python解决线性规划问题
在建立了数学模型之后,我们可以使用Python中的SciPy库来求解这个线性规划问题。SciPy库提供了许多优化算法,其中linprog函数可以用于求解线性规划问题。
3.1 导入必要的库
首先,我们需要导入必要的库:
import numpy as np from scipy.optimize import linprog 3.2 定义目标函数系数
在求解问题时,SciPy的linprog函数默认是用于最小化问题的。因此,我们需要将最大化问题转换为最小化问题。具体来说,我们可以将目标函数的系数取负。
目标函数的系数为:c=[−30,−20]
在Python中定义目标函数系数:
c = [-30, -20] 3.3 定义不等式约束矩阵和向量

在Python中,我们可以定义约束矩阵和向量如下:
A = [[2, 1], [1, 2]] b = [60, 40] 这里,A 是一个二维数组,表示约束条件的系数矩阵,每一行对应一个不等式约束条件,每一列对应一个决策变量。b 是一个一维数组,表示每个约束条件的右端常数项。
- 矩阵 A:每一行代表一个约束条件,每一列代表一个决策变量。在我们的例子中,第一行 [2, 1] 表示第一个约束条件 2x1+x2≤60,第二行 [1, 2] 表示第二个约束条件x1+2x2≤40。
- 向量 b:每个元素表示一个约束条件的右端常数项。对于我们的例子,向量 b 中的元素分别是 60 和 40,对应两个约束条件的右端值。
3.4 定义变量的边界
在实际的生产问题中,变量的取值范围通常是有限制的。对于我们的例子,每天生产的产品数量不能为负,因此我们需要设置变量的边界条件。
非负约束
线性规划问题中的非负约束是指决策变量必须是非负数,即:
x1≥0 x2≥0
这些非负约束条件确保了我们的生产数量是合理的(即,不能生产负数的产品)。
变量边界在SciPy中的表示
在SciPy的linprog函数中,变量的边界可以通过bounds参数来指定。每个决策变量的边界条件可以用一个元组表示,元组的第一个元素是变量的下界,第二个元素是变量的上界。如果变量没有上界,可以用None表示。
x_bounds = [(0, None), (0, None)] 这里,(0, None) 表示变量的下界是0,上界没有限制,即变量必须是非负的。
- 变量边界定义:我们用一个列表来表示每个变量的边界。列表中的每个元素是一个元组,元组的第一个元素表示变量的下界,第二个元素表示变量的上界。在我们的例子中,我们定义了两个变量 x1 和 x2,它们的边界条件都是非负的,因此我们用
(0, None)来表示它们的边界。- 意义和应用:非负约束条件确保了我们的生产计划是现实可行的,因为生产的数量不能为负数。这在实际应用中是非常重要的,可以防止在优化过程中出现不合理的解。
3.5 求解线性规划问题
在定义了目标函数的系数、约束条件和变量的边界之后,我们可以使用SciPy的linprog函数来求解这个线性规划问题。linprog函数是SciPy库中用于求解线性规划问题的主要函数。
调用linprog函数
linprog函数的基本调用方式如下:
res = linprog(c, A_ub=A, b_ub=b, bounds=x_bounds, method='highs') 其中:
c:目标函数的系数向量A_ub:不等式约束条件的系数矩阵b_ub:不等式约束条件的右端常数项向量bounds:变量的边界条件method:求解方法,这里我们使用highs方法,这是SciPy推荐的高效求解方法之一
- 目标函数的系数向量
c:之前定义的目标函数的系数向量[-30, -20]。注意这里我们将最大化问题转换为最小化问题,因此系数取负。- 不等式约束条件的系数矩阵
A_ub:定义了每个约束条件的系数矩阵[[2, 1], [1, 2]]。- 不等式约束条件的右端常数项向量
b_ub:对应于不等式约束的右端常数项向量[60, 40]。- 变量的边界条件
bounds:定义了变量的取值范围,确保变量是非负的。- 求解方法
method:指定使用highs方法,这是SciPy中一个高效的线性规划求解器。
3.6 输出结果
在求解完成之后,我们需要输出结果。结果对象res包含了优化的详细信息,包括最优解和最优目标函数值。
获取和解释最优解
最优解是指在满足所有约束条件的情况下,使目标函数达到最优值的决策变量值。在我们的例子中,最优解是每天应该生产的产品A和产品B的数量。
print('Optimal value:', round(res.fun * -1, ndigits=2)) # 恢复最大化问题的目标函数值 print('x:', res.x) 这里,res.fun 是最优目标函数值,因为我们最初将目标函数系数取了负,所以需要乘以-1来恢复最大化问题的目标函数值。res.x 是最优解,即最优的 x1 和 x2 的值。
4. 结果解释和应用
在得到线性规划问题的求解结果之后,我们需要对结果进行解释和应用。最优解和最优目标函数值对于实际的生产计划具有重要的指导意义。
4.1 结果解释
- 最优目标函数值:1400。这个值表示在满足所有资源约束的情况下,最大化的总利润为1400美元。
- 最优解:每天生产20个单位的产品A和10个单位的产品B。这是指在所有约束条件下能够使总利润最大化的最优生产计划。
4.2 应用
最优解对于工厂的生产计划具有重要的指导意义。通过按照最优解安排生产,工厂可以确保资源的有效利用,最大化利润。
具体来说,工厂应该每天生产20个单位的产品A和10个单位的产品B。这将使得总利润最大化,同时不超过每天可用的资源限制。通过这种方式,工厂可以实现资源的最佳配置,提高生产效率和经济效益。
4.3 验证结果
为了验证结果的正确性,我们可以检查最优解是否满足所有约束条件:
资源1的使用情况: 2×20+1×10=40+10=50≤60
资源2的使用情况: 1×20+2×10=20+20=40≤40
可以看到,最优解不仅最大化了总利润,而且满足所有约束条件。这表明我们的线性规划模型和求解过程是正确的,求解结果是合理的。
5. 扩展阅读
5.1 扩展阅读
线性规划问题在实际中有很多应用,如物流运输、生产计划、资源分配等。除了SciPy,其他常用的优化库还包括PuLP和Gurobi。
- PuLP:PuLP是一个开源的线性规划工具,可以与各种求解器结合使用。它提供了简单易用的接口,适合用于教学和简单的优化问题。
- Gurobi:Gurobi是一款高效的商业优化软件,支持求解线性规划、整数规划和其他优化问题。它具有强大的求解能力,适用于大规模和复杂的优化问题。
5.2 线性规划的其他类型
多目标优化:多目标优化考虑多个目标函数同时进行优化。例如,一个工厂可能希望在最大化利润的同时最小化污染物排放。多目标优化可以通过加权求和法或Pareto最优解来解决。
带有等式约束的线性规划:在约束条件中包含等式约束。例如,某些资源的使用量必须精确等于特定值。等式约束可以用于表示这些严格的资源限制或平衡条件。
混合整数线性规划:决策变量不仅包括连续变量,还包括整数变量。例如,在生产计划中,某些产品的生产数量必须为整数。混合整数线性规划可以通过将部分决策变量定义为整数来解决这些问题。
代码
import numpy as np from scipy.optimize import linprog # 定义目标函数系数 # 我们希望最大化 30x1 + 20x2 # 在使用 linprog 时,我们需要将这个目标函数转化为最小化问题 # 因此我们取负,变为最小化 -30x1 - 20x2 c = [-30, -20] # 定义不等式约束矩阵和向量 # 不等式约束如下: # 2x1 + x2 <= 60 # x1 + 2x2 <= 40 # 转化为矩阵形式 A @ x <= b A = [[2, 1], [1, 2]] b = [60, 40] # 定义变量的边界 # x1 >= 0 # x2 >= 0 x_bounds = [(0, None), (0, None)] # 使用 linprog 函数求解线性规划问题 res = linprog(c, A_ub=A, b_ub=b, bounds=x_bounds, method='highs') # 输出结果 print('Optimal value:', round(res.fun * -1, ndigits=2)) # 恢复最大化问题的目标函数值 print('x:', res.x) # 结果解释 # 最优目标函数值 optimal_value = round(res.fun * -1, ndigits=2) # 最优解 optimal_solution = res.x print(f"在满足资源约束的情况下,最大化的总利润为:{optimal_value} 美元") print(f"每天生产 {optimal_solution[0]} 个单位的产品A 和 {optimal_solution[1]} 个单位的产品B") # 验证结果是否满足所有约束条件 # 资源1的使用情况 resource1_usage = 2 * optimal_solution[0] + optimal_solution[1] # 资源2的使用情况 resource2_usage = optimal_solution[0] + 2 * optimal_solution[1] print(f"资源1的使用情况:{resource1_usage} 小时(<= 60 小时)") print(f"资源2的使用情况:{resource2_usage} 小时(<= 40 小时)") # 验证是否满足所有约束条件 if resource1_usage <= 60 and resource2_usage <= 40: print("最优解满足所有约束条件。") else: print("最优解不满足所有约束条件。") 结果

总结
建立线性规划模型,以解决生产优化问题。通过定义决策变量、目标函数和约束条件,使用Python的SciPy库中的linprog函数求解模型,并验证结果的合理性。最终,确定了在资源限制条件下最大化利润的最优生产方案.

