一、前言
前面讲了KNN算法,这里我们来学习一下支持向量机的模型使用,看一下用支持向量机的方法,是否可以完成了之前KNN算法中的那个“约会网站配对”的算法实现嘞。
二、什么为支持向量机
我们跟着老师的要求来,从四个层次来理解一下支持向量机的操作:
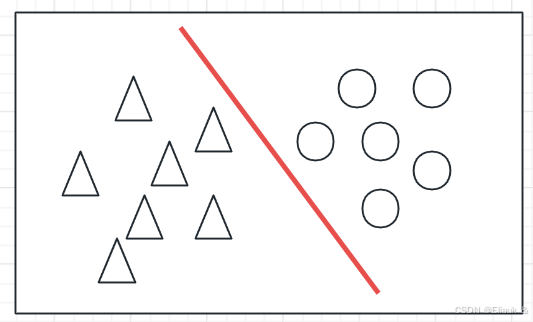
(1)支持向量
就是我们在两堆数据中,找到一个超平面,它可以使两堆数据尽可能多的正确的分开,同时使分开的两堆数据点距离我们的这个平面的分类距离最远。
(2)允许误差
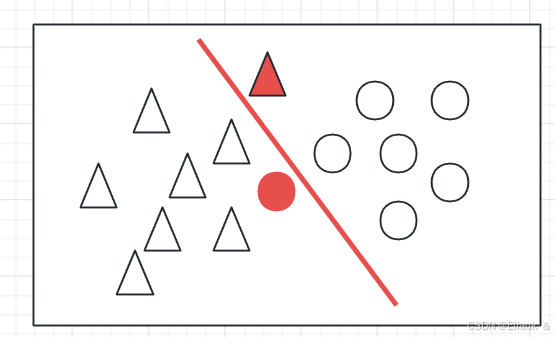
即我们在划分的时候,可能出现一些数据,划分的并不是很准确,可能会有一定的误差,但是这些误差都是允许出现的。
(3)非线性可分
指的是有些非线性的数据,它杂糅在平面中,我们不能用一条线,将这两类数据分开时,我们可以尝试通过将数据映射到三维的空间,此时在三维空间,找到一个划分平面,再将这个平面映射到二维平面(此时的线就可能不是直线了),也是可以的,这是一种降维打击的思考方向。
(4)使用核函数
核函数的做法也是将数据从低纬度映射到高纬度,但是核函数可以事先在低纬度进行计算,实现的效果可以直接展示在高纬度,去除了在高纬度计算的过程。
PS:这个其实不好理解,我下来看哈相关资料后,看哈能不能做一个核函数的推理过程来看看。
三、实现支持向量机
使用我们的scikit-learn库来实现我们的支持向量机的操作。
下载语句,在pycharm终端输入等待即可
pip install scikit-learn -i https://pypi.tuna.tsinghua.edu.cn/simple/
SKlearn的简单使用
1、导入库
from sklearn import svm2、定义模型
# 原始的支持向量集,还没有设置核函数等操作 model = svm.SVC()3、模型函数
# trainingMat为训练(样本)数据,hWLabels为数据的标签 model.fit(trainingMat, hWLabels)4、模型测试
# vectorUnderTest为我们的测试数据 model.predict(vectorUnderTest)四、支持向量机实践
这里我们就用KNN算法中的“约会网站配对”的例子来测试我们支持向量机的准确性,完整代码如下:
import numpy as np import KNN_Package as K from sklearn import svm def file2matrix(filename): fr = open(filename) numberOfLines = len(fr.readlines()) # 定义一个numberOfLines行,3列的零矩阵 # 一定要加两个括号 returnMat = np.zeros((numberOfLines, 3)) # 标签向量 classLabelVector = [] fr.close() fr = open(filename) index = 0 for line in fr.readlines(): # 去掉每一行的前后空格 line = line.strip() # 根据tab将数据切割出来,listFromLine就成了一个字符串列表 listFromLine = line.split("\t") # listFromLine[0:3]将listFromLine的前三列赋值给returnMat[]数组,因为returnMat有numberOfLines行,就会执行numberOfLines次操作 returnMat[index, :] = listFromLine[0:3] # listFromLine[-1]表示最后一列 if listFromLine[-1] == 'didntLike': classLabelVector.append(1) elif listFromLine[-1] == 'smallDoses': classLabelVector.append(2) elif listFromLine[-1] == 'largeDoses': classLabelVector.append(3) index += 1 fr.close() return returnMat, classLabelVector datingDataMat, datingLabels = file2matrix("D:/python工具/素材处/KNN(二)/DataText.txt") # 数据归一化处理 # 0-1标注化 def autoNorm(dataSet): # min(0)按特征的列选取,min(1)按照特征的行选取 minVals = dataSet.min(0) maxVals = dataSet.max(0) # shape记录了dataSet的行和列 normDataSet = np.zeros(dataSet.shape) normDataSet = (dataSet - minVals) / (maxVals - minVals) return normDataSet dataSet = autoNorm(datingDataMat) m = 0.8 # shape[0]表示行、shape[1]表示列 dataSize = dataSet.shape[0] print("数据集的总行数:", dataSize) # 80%作为训练 20%作为测试 trainSize = int(m * dataSize) testSize = int((1 - m) * dataSize) # 原始的支持向量集,还没有设置核函数等操作 model = svm.SVC() model.fit(dataSet[0:trainSize, :], datingLabels[0:trainSize]) result = [] error = 0 # 调用封装好的KNN函数 for i in range(testSize): # dataSet[trainSize + i - 1, :]表示dataSet矩阵中的第trainSize + i - 1行元素(包含对应的所有列) # dataSet[0:trainSize, :]表示一个从0~trainSize行,包含对应所有列的矩阵 # datingLabels[0:trainSize]表示截取列表datingLabels中的0~trainSize个元素 # 通过reshape函数规整一下数据 result = model.predict(dataSet[trainSize + i - 1, :].reshape(1, -1)) if result != datingLabels[trainSize + i - 1]: error += 1 print('错误率:', error / testSize) 效果:
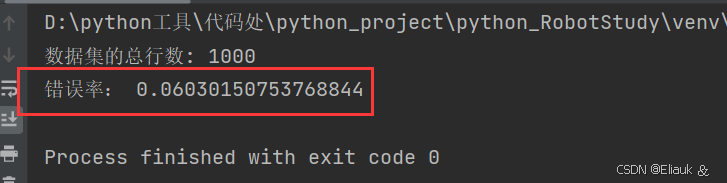
从效果来看,原生的支持向量机的操作的错误率为6.03%要比我们的KNN算法的准确性要差一点,但是,别忘了我们的支持向量机的模型定义的时候,是用的原生的,还没有设置我们的核函数那些操作的,所以具体情况要具体分析。
五、总结
博主也是初学者,有很多不懂的地方,如果有说错的地方,欢迎大家指正。最后,该内容是跟着B站up主【abilityjh】老师学习的,大家可以去看该老师的视频学习!
