支持向量机(SVM)中的核函数是支持向量机能够处理非线性问题并在高维空间中学习复杂决策边界的关键。核函数在SVM中扮演着将输入特征映射到更高维空间的角色,使得原始特征空间中的非线性问题在高维空间中变得线性可分。
一、SVM是什么?
很久以前的情人节,公主被魔鬼绑架了,王子要去救公主,魔鬼和他玩了一个游戏。魔鬼在桌子上似乎有规律放了两种颜色的球,说:“你用一根棍分开它们?要求:尽量在放更多球之后,仍然适用。”
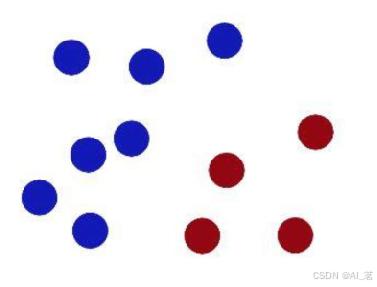
第一次,王子这么放: 魔鬼又摆了更多的球,有一个球站错了阵营:

SVM就是试图把棍子放在最佳位置, 现在魔鬼即使放了更多的球,
好让在棍的两边有尽可能大的间隙。 棍仍然是一个好的分界线。

现在魔鬼又玩了一个花招, 王子拍了一下桌子,所有的球都飞了起来,
将球如下摆放。 然后拿了一张纸插在了两种颜色球的中间。
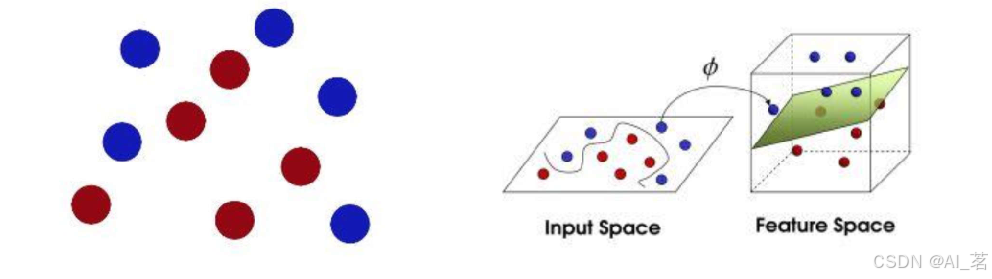
再后来,我们把这些球叫做[data->数据]
把棍子叫做[classifier ->分类器]
最大间隙trick 叫做[optimization ->最优化],
拍桌子叫做[kernelling ->核函数]
那张纸叫做[hyperplane ->超平面]
SVM核心:选择一个最佳的一条线(超平面)
二、SVM有哪些常用的核函数?
1.多项式核函数:
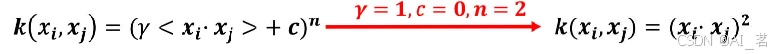
假如有两个数据x1=(x1x2),x2=(y1y2),如果数据在二维空间无法线性可分,我们通过核函数将其从二维空间映射到更高的三维空间,那么此时:

更具体的例子:x1=(1,2),x2=(3,4)
(1)转换到三维再内积(高维运算)



(2)先内积,再平方(低维运算)

2.高斯核函数:

rbf:又称径向基函数
对于数据点1转换到二维空间:
(1)找两个地标或者说两个数据点,将他们作为一个正态分布的均值。->比如-2和1
(2)计算数据到地标的距离:
(3)指定 y 为 0.3 。[y必须大于0]
(4)计算新的坐标 
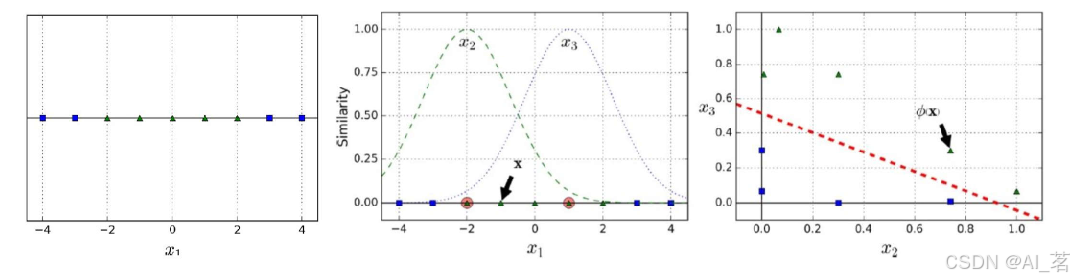
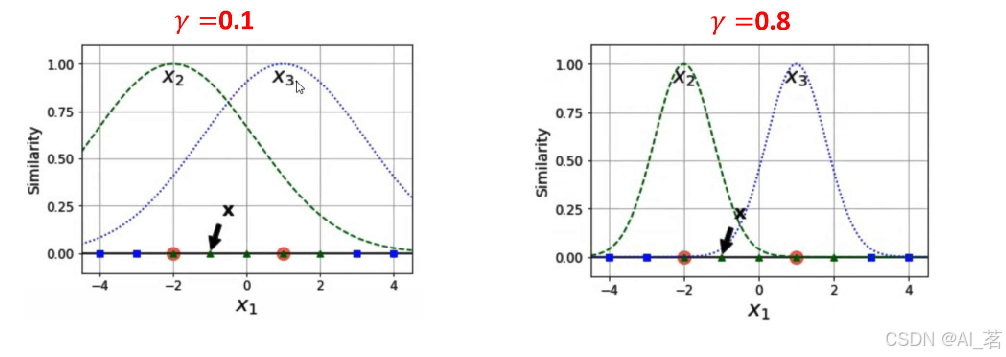
谈一下y值:
(1)当y值越小的时候,正态分布越胖, (2)当y值越大的时候,正态分布越瘦,
辐射的数据范围越大,过拟合风险越低。 辐射的数据范围越小,过拟合风险越高。
优缺点介绍:
优点:
1)有严格的数学理论支持,可解释性强,不同于传统的统计方法能简化我们遇到的问题。
2)能找出对任务有关键影响的样本,即支持向量。
3)软间隔可以有效松弛目标函数。
4)核函数可以有效解决非线性问题。
5)最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而
不是样本空间的维数,这在某种意义上避免了“维数灾难”。
6)SVM在小样本训练集上能够得到比其它算法好很多的结果。
缺点:
1)对大规模训练样本难以实施。
SVM的空间消耗主要是存储训练样本和核矩阵,当样本数目很大时该矩阵的存储和计算将
耗费大量的机器内存和运算时间。超过十万及以上不建议使用SVM。
2)对参数和核函数选择敏感。
支持向量机性能的优劣主要取决于核函数的选取,所以对于一个实际问题而言,如何根据实际的数据模型选择合适的核函数从而构造SVM算法。目前没有好的解决方法解决核函数的选择问题。
3)模型预测时,预测时间与支持向量的个数成正比。当支持向量的数量较大时,预测计算复杂度较高。
