一、冒泡排序
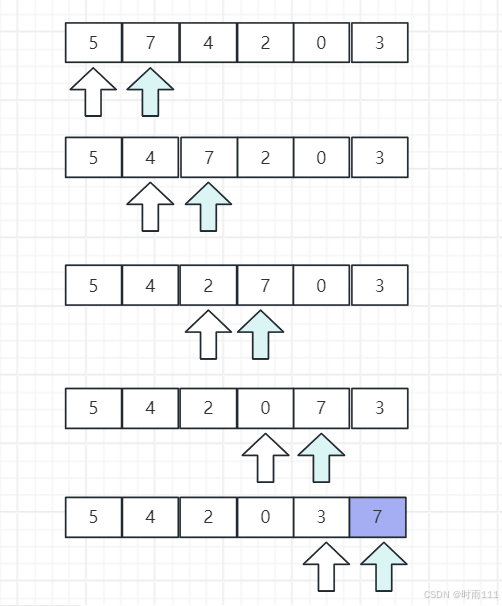
思想:前后相邻的两个数两两进行交换,如果前面的数大于后面的就交换,否则不交换,直到最大的数到达最后,循环这一过程直至全部排序完成。
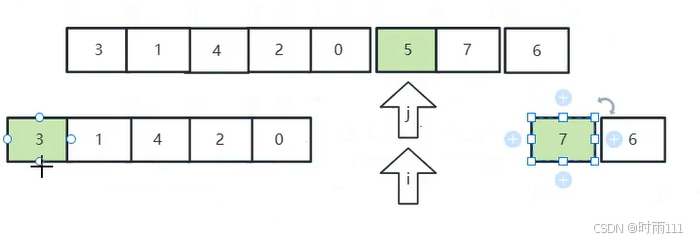
一趟遍历下来排好了7的位置,然后再从头开始这次只需要拍好7前面的数组就好了,每次循环中最大的那个数,都会排好位置,就像一个气泡一个一个的到达排好的位置,所以叫做冒泡排序
时间复杂度是O(n^2)
代码:
public static void BubbleSort(int[] arr) { int n = arr.length; for(int i=0;i<n-1;i++) { for(int j = 0;j<n-i-1;j++) { if(arr[j]>arr[j+1]) { int t = arr[j]; arr[j] = arr[j+1]; arr[j+1] = t; } } } }二、快速排序
思路
1、默认待排序数组当中的第一个为基准数
2、定义j游标,从后往前移动,找比基准数小的,找到之后停止
3、定义i游标,从前往后移动,找比基准数打的,找到之后停止
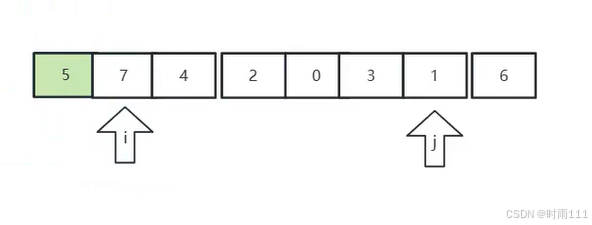
5.i和j两个游标指向的值进行交换,
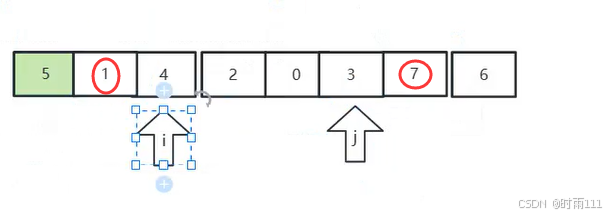
6.重复2,3,4步直到两个游标指向同一个位置位置,此时该位置左边的数字都不大于基准数,右边的数都不小于基准数,所以该位置就是基准数在排好序的列表中的正确位置
ij在5处相遇,将数组分为左右两部分
7.交换基准数和相遇位置的值,以相遇位置为分割,将原数组分为左右两个待排序的数组,目前基准数以排序号,此时只需要将左右两边的待排序数组也排好序就行,正好分别调用快速排序函数,形成递归
继续拆分
public static void QuickSort(int[] arr,int left,int right) { if(left>=right) { return; } int base = arr[left]; int i = left; int j = right; while(i!=j) { while(arr[j]>=base&&i<j) { j--; } while(arr[i]<=base&&i<j) { i++; } int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } arr[left] = arr[i]; arr[i] = base; QuickSort(arr,left,i-1); QuickSort(arr,i+1,right); }时间复杂度
最好情况是:n*logn
最坏情况是:n^2
三、堆排序:
步骤:
1.利用完全二叉树构建大顶堆
2.将堆底元素和堆顶元素进行交换,除了堆底元素外,其余元素继续构建大顶堆
3.重复2
完全二叉树:要求所有数据从左到右,从上到下构建(除了最后一层的叶节点,其他层均已满,并且最后一层叶节点全在最左边)
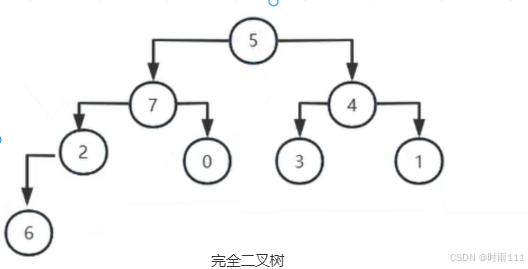
大顶堆:整个树每个父节点的值的值都大于等于左右孩子的值
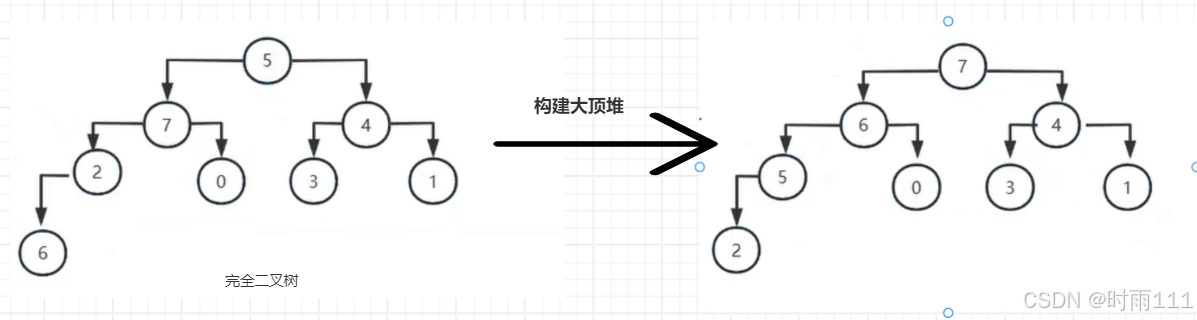
其中7就是大顶堆的堆顶元素,根据大顶堆的定义我们不难推断出,在大顶堆中对顶元素肯定是最大的 。
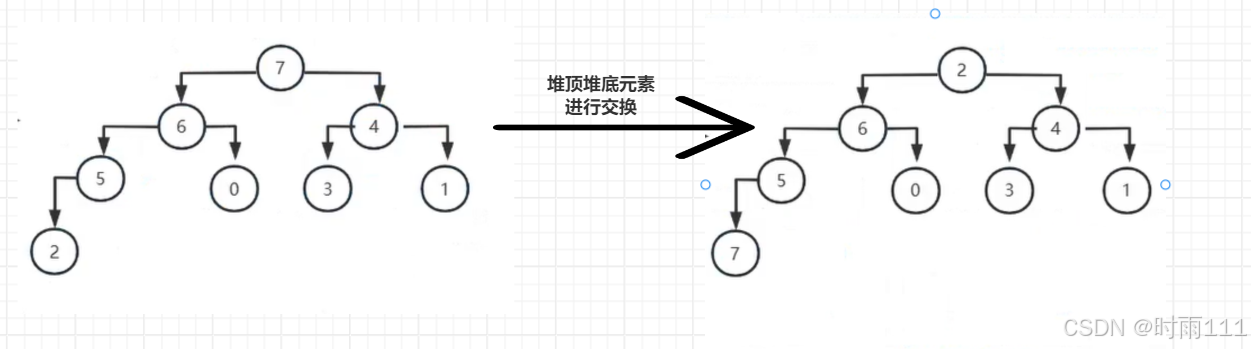
除堆底元素外继续构建大顶堆
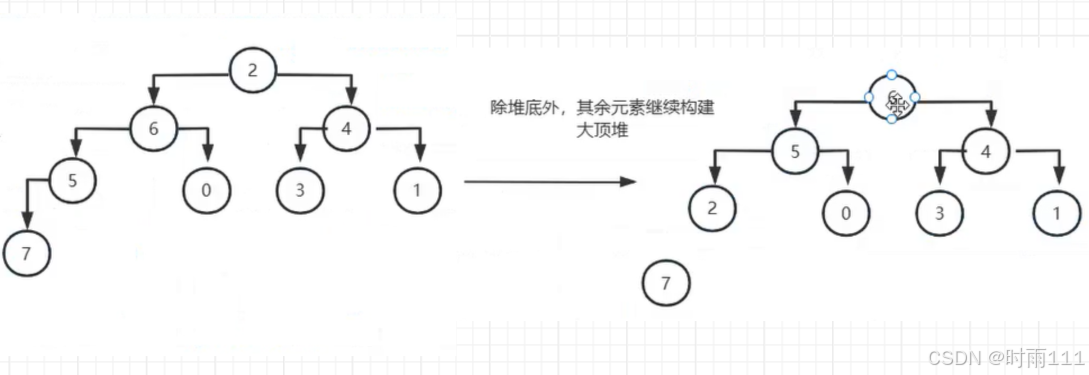
堆底堆顶元素进行交换,剩余元素继续构建大顶堆
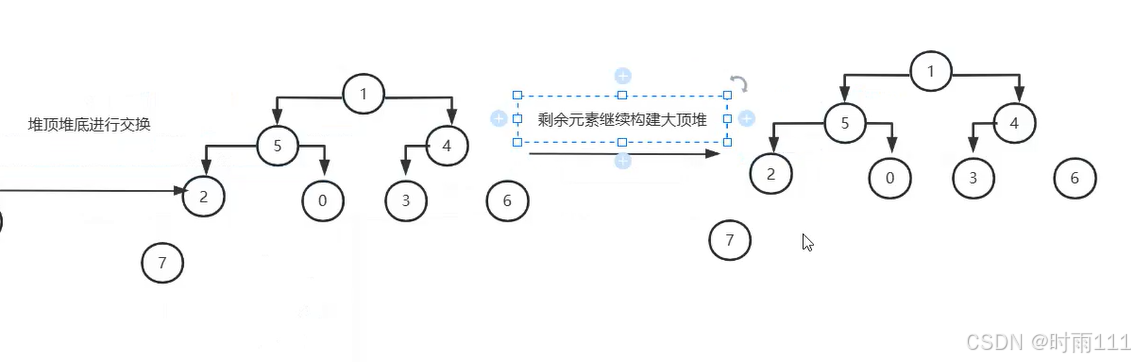
持续这一过程,最终会获得排序好的数组。
下面我们将数组的索引到标记到完全二叉树上,如下图
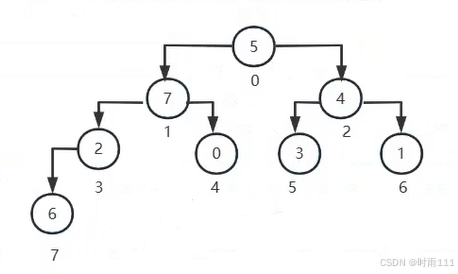
我们不难发现父节点和子节点编号间的关系如下
arr[i]的左孩子是arr[2i+1]
arr[i]的左孩子是arr[2i+2]
arr[i]的父节点是arr[(i-1)/2]
所以一个节点是否满足大于等于其左右孩子的条件就可以写成
arr[i] >= arr[2i+1]&&arr[i]>=arr[2i+2]
完成构建大顶堆的数组:
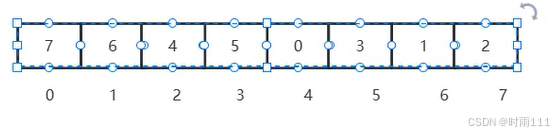
交换堆顶堆底元素,就是将7和2进行交换
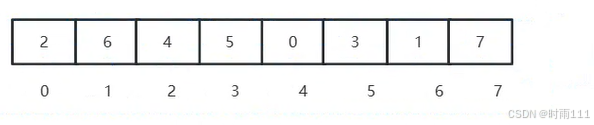
除7以外其他数据继续构建大顶堆
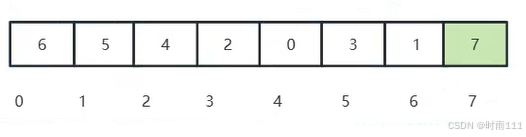
我们可以看出来在数组中我们仍然可以完成堆排序排序的要求。

刚才我们直接使用了大顶堆,让大家明白堆排序的过程,却没有进行大顶堆构建的步骤,下面我们一起来看看大顶堆是如何构建的。
思路:从后往前一次遍历所有节点是否符合大顶堆,如果遇到不符合的大顶堆条件的就进行调整
首先没有子节点的节点必然符合大顶堆的要求,所以可以从6一直遍历到0,现在遍历到2节点了,那么现在出现了一个问题,我们该如何去判断一个有子节点的节点是否符合大顶堆,以及该如何去调整呢?
1.定义parent游标指向当前要检查的节点
2.如果该节点无子节点,那么它符合大顶堆,如果有孩子,那么定义child游标指向parent的左孩子,在完全二叉树中如果有孩子那么一定有左孩子。
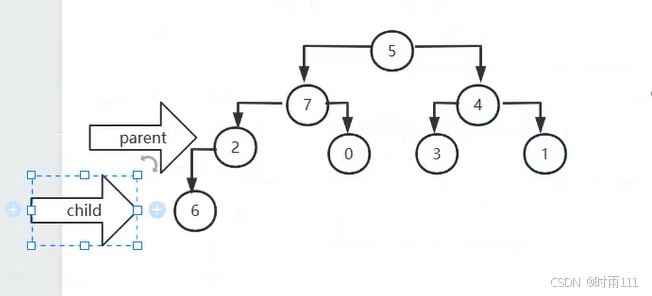
3.判断有没有右孩子,如果有右孩子,那么child游标指向左右孩子中的最大值
4.父子节点值(parent指向的节点和child指向的节点值)进行比较,如果parent节点值更大,则该节点符合大顶堆的要求
5.如果parent节点的值小,对parent指向的节点进行调整
怎么调整呢?先将parent和child游标指向的节点值进行交换,交换完成之后,让游标parent指向child,让child指向左右孩子中的最大值,继续进行比较parent指向的节点和child指向的节点的值,重复4,5,直到parent指向节点的值更大(符合大顶堆),或者child指向的空(没有子节点,符合大顶堆要求)
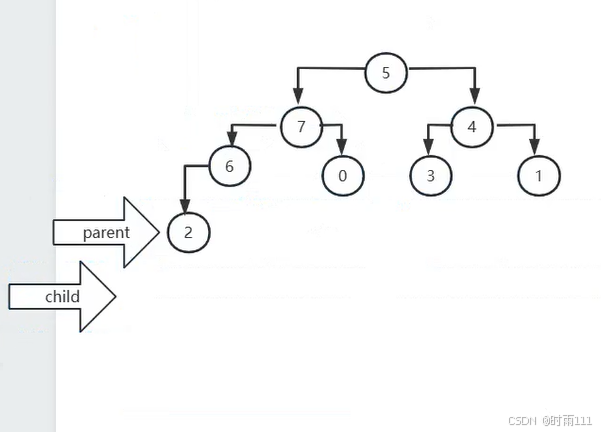
之后遍历到了节点4,7均符合大顶堆要求,最后parent指向5,child指向7如图
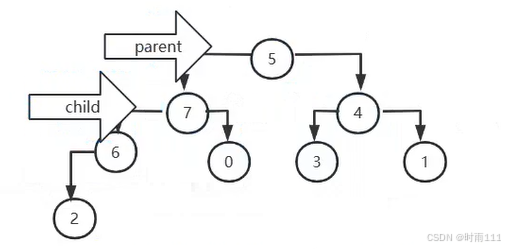
父子节点值进行交换
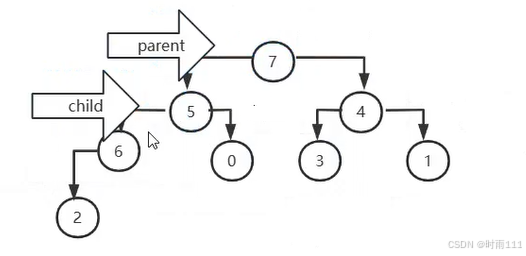
然后让parent指向5,child指向6
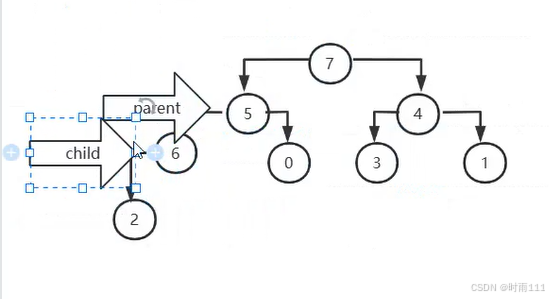
交换5,和6,移动游标,如下
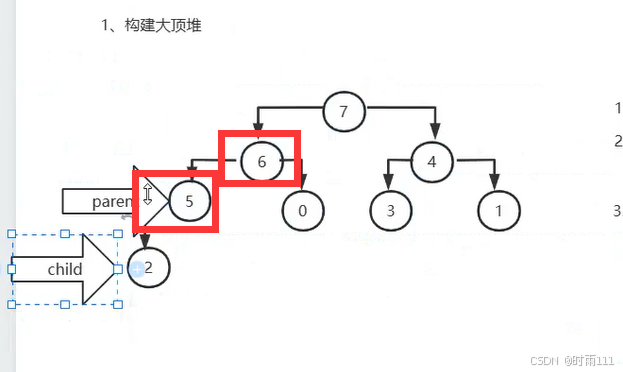
目前已经遍历完整棵树了,也完成了了一个大顶堆的建立
现在需要进入到堆排序的第二步了
步骤2:交换堆顶堆底元素,其余节点继续构建大顶堆
(1)parent指向堆顶元素,child指向左右孩子中的最大值(由于只有堆顶元素发生了改变,堆底不再参与构建大顶堆所以,只需要检测以及调整对顶节点是否满足大顶堆要求即可)
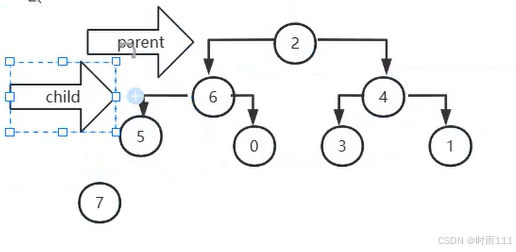
(2父子节点值(parent指向的节点和child指向的节点值)进行比较,如果parent节点值更大,则该节点符合大顶堆的要求
(3)如果parent节点的值小,对parent指向的节点进行调整,将parent和child游标指向的节点值进行交换,交换完成之后,让游标parent指向child,让child指向左右孩子中的最大值,继续进行比较parent指向的节点和child指向的节点的值,重复4,5,直到parent指向节点的值更大(符合大顶堆),或者child指向的空(没有子节点,符合大顶堆要求)
重新构建好的大顶堆如下
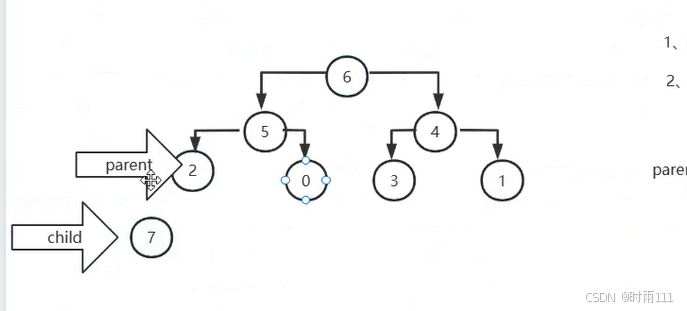
重复步骤2直到完全二叉树中只有一个节点,就完成排序了
下面我们来看代码,
首先我们写一个判断当前节点是否满足大顶堆,若不符合就可对其进行调整的函数。
/** * 判断节点是否是符合大顶堆条件,若不符合进行调整 * length是参与构建大顶堆的节点数 */ public static void adjust(int[] arr,int parent,int length){ int child = parent*2+1; while(child<length){ //判断是否有右孩子,并比较左右孩子大小 if(child+1<length&&arr[child]<arr[child+1]){ //若右孩子大,则child指向右孩子 child++; } if(arr[child]>arr[parent]){ //不符合大顶堆 int temp = arr[parent]; arr[parent] = arr[child]; arr[child] = temp; parent = child; child = 2*child+1; }else { //符合大顶堆 break; } } }然后对堆排序进行测试,我是再main方法中进行的,当然小伙伴们也可以将其,封装成一个函数。
public static void main(String[] args) { int[] arr = {5,7,4,2,0,3,1,6}; //第一步从后向前遍历二叉树的节点,并完成调整(adjust)以构建大顶堆 for(int p = arr.length-1;p>=0;p--){ //定义p是指向需要检测/调整的节点游标 adjust(arr,p,arr.length); } //第二步堆顶堆底元素进行交换,并维护堆顶元素 for(int i = arr.length-1;i>=0;i--){ //定义游标i让其一直指向需要构建的顶堆,的堆底元素 int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; //维护堆顶元素 //i是需要参与构建大顶堆的节点数 adjust(arr,0,i); } System.out.println(Arrays.toString(arr)); }堆排序的时间复杂度是n*logn
上面我们用的是大顶堆,现在我们能不能尝试使用小顶堆完成堆排序呢?大家可以动手试一下
小顶堆: 整个树每个父节点的值的值都小于等于左右孩子的值