线性代数
本章代码在chapter_preliminaries/linear-algebra.ipynb中
标量
标量:是由一个元素的张量表示
标量的计算:
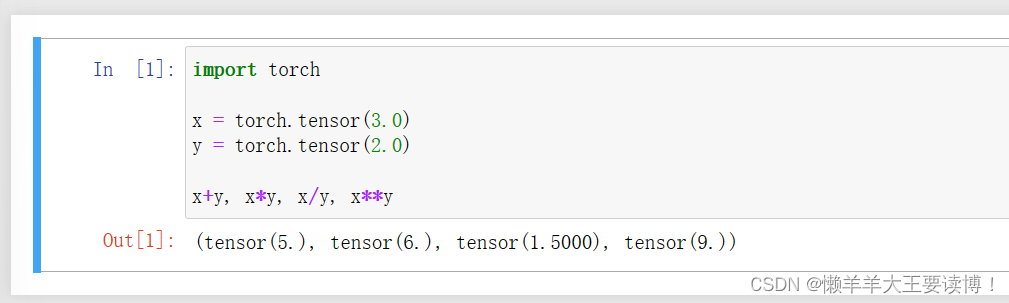
向量:向量可以被视为标量值组成的列表,通过下标索引来引用向量中的任意元素

内置len()函数来访问张量的长度:
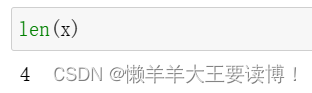
.shape访问形状,当只有一个轴的张量,形状只有一个元素
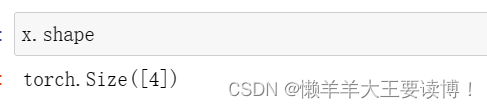
矩阵
创建一个形状为m×n的矩阵,通过.T访问矩阵的转置:

对称矩阵: 
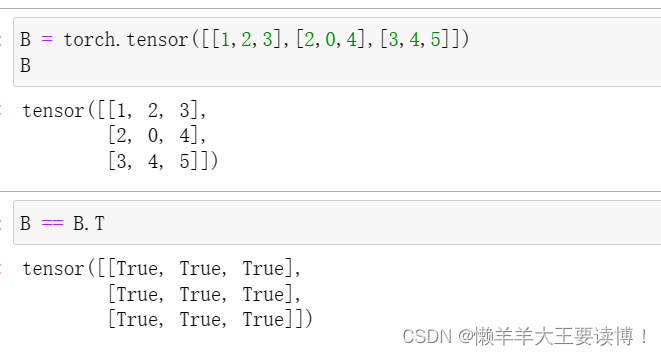
张量
创建2个3行4列矩阵,同样形状的张量可以相加:
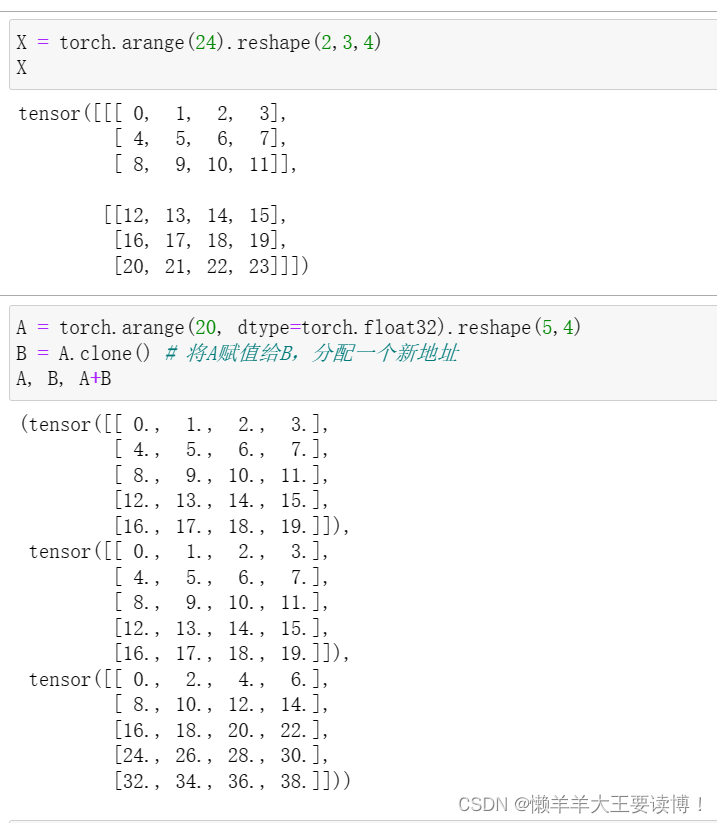
两个矩阵的按元素乘法称为Hadamard积(Hadamard product)(数学符号⊙):

将张量乘以或加上一个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘:

降维
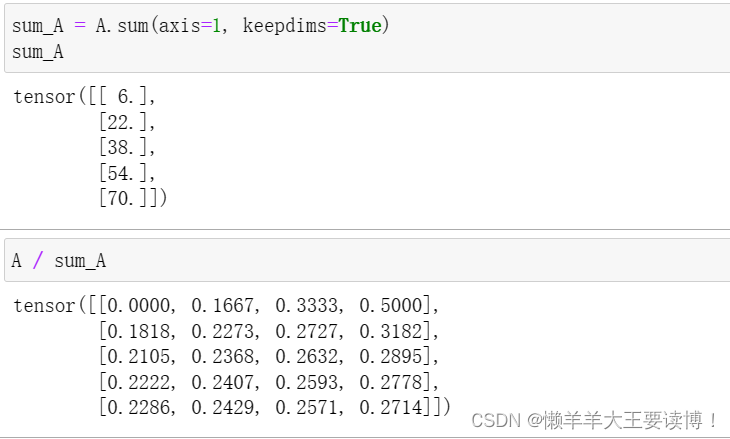
计算其元素的和

指定张量沿哪一个轴来通过求和降低维度,axis = 0指沿着轴0降维,即轴0在输出形状中消失

求平均值(mean或average):

非降维求和
沿某个轴计算A元素的累积总和, 比如axis = 0(按行计算),可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。

点积(Dot Product)
通过执行按元素乘法,然后进行求和来表示两个向量的点积

矩阵-向量积

矩阵-矩阵乘法

范数
Frobenius范数(Frobenius norm)是矩阵元素平方和的平方根
L1范数表示为向量元素的绝对值之和

矩阵计算
自动求导
本章代码在chapter_preliminaries/autograd.ipynb中
一个例子
首先创建一个x和y:
import torch x = torch.arange(4.0) x # tensor([0., 1., 2., 3.]) # 在计算y关于x的梯度之前需要一个地方存储梯度 x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True) x.grad # 默认值是None,用来访问梯度 y = 2 * torch.dot(x, x) y # tensor(28., grad_fn=<MulBackward0>) 补充:上述代码中requires_grad 表达的含义是:这一参数是否保留(或者说持有,即在前向传播完成后,是否在显存中记录这一参数的梯度,而非立即释放)梯度,等待优化器执行optim.step()更新参数。
当requires_grad = False,则不保留梯度,因此即便在optimizer中注册了参数,也没有梯度可以用来更新参数,因此参数不变。不过不影响
梯度继续反向传播,即假设某一层(例如第三层)参数的requires_grad为False或True,前面层(第1或2层)参数的梯度都不变。
当requires_grad = True,则在前向计算后保留梯度,用于optimizer更新参数。但如果没有在optimizer中注册参数,那么即便保存了梯度
也无法更新参数。
参考:原文链接:https://blog.csdn.net/zyk910811/article/details/131580109
通过调用反向传播函数来自动计算y关于x每个分量的梯度
y.backward() x.grad # tensor([ 0., 4., 8., 12.]) x.grad == 4 * x # tensor([True, True, True, True]) 计算x的另一个函数时,首先要清除之前的梯度值
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值 x.grad.zero_() y = x.sum() y.backward() x.grad # tensor([1., 1., 1., 1.])非标量变量的反向传播
对非标量调用backward需要传入一个gradient参数,该参数指定微分函数关于self的梯度。
x.grad.zero_() y = x * x y.sum().backward() # 等价于y.backward(torch.ones(len(x))) x.grad # tensor([0., 2., 4., 6.])补充:gradient参数:http://t.csdnimg.cn/A0VjU
分离计算
x.grad.zero_() y = x * x u = y.detach() # 把y当作一个常数而不是关于x的函数 z = u * x z.sum().backward() x.grad == u # tensor([True, True, True, True]) x.grad.zero_() y.sum().backward() x.grad == 2 * x # tensor([True, True, True, True])Python控制流的梯度计算
使用自动微分的一个好处是:即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度。
def f(a): b = a * 2 while b.norm() < 1000: b = b * 2 if b.sum() > 0: c = b else: c = 100 * b return c a = torch.randn(size=(), requires_grad=True) d = f(a) d.backward() a.grad == d / a # tensor(True)