目录
一、背景简介
商场顾客细分旨在深入分析商场顾客群体,为商场提供更精准的营销策略和服务。随着市场经济的发展以及电商平台的崛起,商场竞争日益激烈,如何吸引并留住顾客,提高销售额和市场份额,已成为各大商场关注的焦点。为了实现这一目标,商场需要对顾客进行细分,以便更好地了解顾客需求,提供个性化的商品和服务。本项目通过对消费者收入、支出分数进行分析,将顾客细分为不同群体。在此基础上,商场可以根据不同顾客群体的特点和需求,制定有针对性的营销策略,提高顾客满意度和忠诚度。
项目背景及数据来源:商场顾客细分数据 (kaggle.com)
这个数据集有五个变量,分别是客户id,年龄,性别,年收入,支出分数。想通过这些数据探索用户特点并进行分类,以便为营销团队提供相应的策略,寻找最优价值的目标客户。

在本文,会先进行简单的探索性数据分析,然后使用kmeans将客户分为五类,并讨论五类用户的特点。如有不足之处欢迎探讨~
二、数据分析
1、数据导入
导入数据并查看前五行数据
import numpy as np import pandas as pd import os import matplotlib.pyplot as plt import seaborn as sns plt.rcParams['font.sans-serif']=['SimHei'] #显示中文 # 导入数据 data = pd.read_csv('./Mall_Customers.csv') data.head()
查看数据基本信息。其中一个分类变量,四个数值型变量(包含id)。
data.info()
查看数据大小。共计200条数据。
data.shape![]()
2、探索性数据分析
2.1描述性分析
接下来利用describe函数对数据进行描述性分析。
data.describe()
对于分类型变量可以使用include=np.object查看,如性别变量有2个可能取值,数量最多的是“Famale”(男性),有112条数据。
data.describe(include=np.object).T # 分类变量描述性分析 
查看缺失值,并没有缺室值。
print(data.isnull().sum()) # 查看缺失值
2.2可视化分析
查看样本中男女各有多少人,并画出柱状图。
print(data['Gender'].value_counts()) sns.countplot(x='Gender', data=data) 

对于年收入、支出分数和年龄绘制直方图。由图中可以看到年收入呈现右偏分布,大部分人年收入都在85k美元以下;支出分数分布较为正态,分数在40——60的人居多;年龄分布直方图可以看出,右偏分布,年轻人居多。
plt.figure(figsize=(15,5),dpi=300) plt.subplots_adjust(wspace =0.3, hspace =0.3) for n,i in enumerate(data[['Annual Income (k$)','Spending Score (1-100)','Age']]): plt.subplot(1,3,n+1) plt.title(i,fontsize=10) plt.grid(linestyle='') data[i].hist()
对变量进行成对分析,发现变量两两间并没有明显的相关关系。
data['Gender_encoded'] = data['Gender'].map({'Male': 0, 'Female': 1}) # 数据变换 with pd.option_context('mode.use_inf_as_na', True): sns.pairplot(data.loc[:,~data.columns.isin(['CustomerID','Gender'])],diag_kind="kde")
2.3数据预处理
# 数据处理 data.drop(['CustomerID','Gender'], axis=1, inplace=True)3、kmeans聚类
K-means是经典的无监督学习方法,因其实现简单和较好的聚类效果,目前被广泛应用。其基本思想是选取样本中k个点为中心进行聚类,将其余样本归到到距离最近的中心,并不断迭代至最好的聚类结果。但由于K-means的初始聚类中心是随机选择的,不同的聚类中心可能会有不同的分类结果。K-means++算法是K-means在初始质心上的优化,基本思路是各初始聚类中心的距离尽可能的远,完整的算法步骤如下:
(1)初始质心的选择。从样本中随机选取一点作为初始质心,计算非质心样本与现有质心样本之间的距离,选择距离最远的样本作为下一个类的质心,不断重复直至找到K个质心;
(2)计算每个样本到各个质心的距离,并将样本分组到最近质心对应的类中;
(3)计算每个类内样本的平均值,并使用该平均值更新类的聚类中心;
(4)重复步骤2与步骤3,直至质心位置的变化小于指定的阈值,或者达到最大迭代次数则停止。
K-means++通过对K-means算法中初始点选择上进行了改进,尽管在计算聚类中心时会花费较多时间,但是在迭代过程中会使得算法更快收敛,且能显著改善分类结果的最终误差。
K-means++算法计算样本间的距离采用的是欧式距离,故需要先将数据进行标准化。标准化的目的是确保每个变量对聚类结果的贡献是平等的,避免某些变量因为数值范围大而占据主导地位。
# 对数据进行标准化 data_Standard=data[['Annual Income (k$)','Spending Score (1-100)']].apply(lambda x: (x - x.mean()) / np.std(x)) data_Standard # from sklearn.preprocessing import StandardScaler # # 标准化数据 # scaler = StandardScaler() # data_Standard = scaler.fit_transform(data)
3.1kmeans聚类最优k值的选取
(1)肘部法
这里k的选取是根据簇内平方和(每个数据点到其所属簇中心的距离之和的平方)来决定的,kmeans.inertia_指的是样本离最近的聚类中心的距离平方和,当其达到一个肘点后会下降很慢。
由图看,大致最优的k在5.
from sklearn.cluster import KMeans wcss=[] for i in range(1,11): kmeans=KMeans(n_clusters=i, init='k-means++',max_iter=300,n_init=10,random_state=0) kmeans.fit(data_Standard) wcss.append(kmeans.inertia_) plt.plot(range(1,11),wcss) plt.title('The Elbow Method') plt.xlabel('Number of clusters') plt.ylabel('WCSS') plt.show()
(2)轮廓系数
根据轮廓系数确定最优的k值。每一个样本i的轮廓系数是(a(i)-b(i))/max(a(i),b(i)),a(i)表示样本i与类间其他样本的平均距离,b(i)表示与其他类样本平均值的最小值。参考:https://blog.csdn.net/J__aries/article/details/129171444
一般地,轮廓系数越高聚类效果越好。
由图可以看出,最优的k为5。
from sklearn.metrics import silhouette_score K=range(2,11) score=[] for k in K: kmeans=KMeans(n_clusters=k, init='k-means++') kmeans.fit(data_Standard) score.append(silhouette_score(data_Standard,kmeans.labels_,metric='euclidean')) plt.plot(K,score,'r*-') plt.xlabel('k') plt.ylabel(u'轮廓系数') plt.title(u'轮廓系数确定最佳的K值')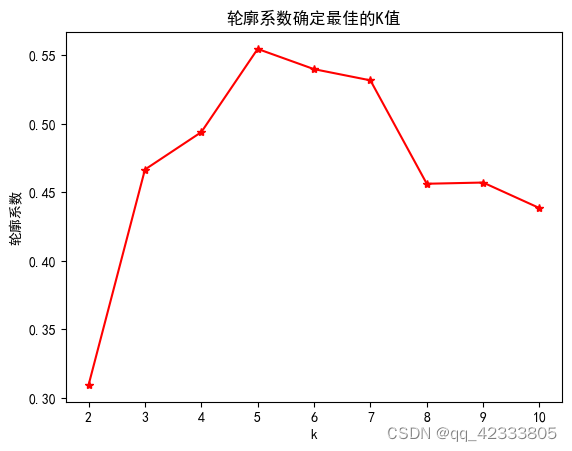
(3)类的平均直径
李航《统计学习方法》中,使用的类的平均直径来决定最优的聚类数k。
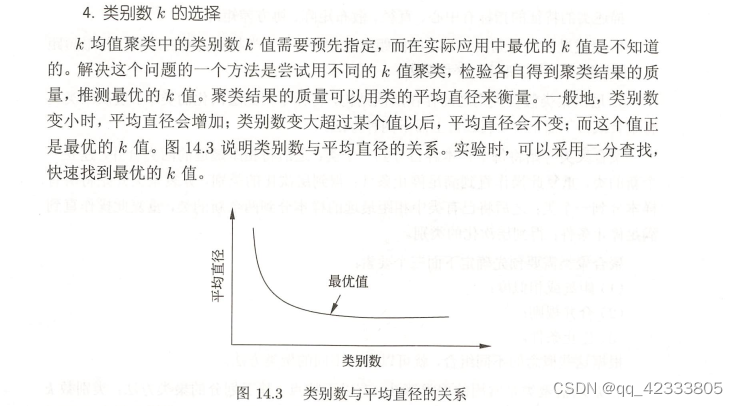
其中类的直径指:类中任意两个样本之间的最大距离,类的平均直径就是所有类的直径再求平均。

一般地,类别数变小时,平均直径会增加,当类别数超过某个值后,平均直径会不变,此时的k值就是最优的。
这种方法比使用WCSS更耗时,因为对于每个簇,它都需要计算所有样本对之间的距离。对于大型数据集,需要考虑优化算法或使用更高效的距离计算方法。
from scipy.spatial.distance import euclidean def cluster_diameter(cluster): """计算簇的直径,即簇内两个样本之间的最大距离""" if len(cluster) < 2: return 0 max_distance = 0 for i in range(len(cluster)): for j in range(i+1, len(cluster)): distance = euclidean(cluster.iloc[i], cluster.iloc[j]) if distance > max_distance: max_distance = distance return max_distance def average_diameter(data, labels): """计算类的平均直径""" unique_labels = set(labels) diameters = [] for label in unique_labels: cluster = data.iloc[labels == label] diameter = cluster_diameter(cluster) diameters.append(diameter) return np.mean(diameters) average_diams = [] # 尝试不同的k值 for k in range(1, 11): kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, n_init=10, random_state=0) kmeans.fit(data_Standard) labels = kmeans.labels_ avg_diam = average_diameter(data_Standard, labels) average_diams.append(avg_diam) plt.plot(range(1,11),average_diams) plt.title('类平均直径确定最佳的K值') plt.xlabel('k') plt.ylabel('类平均直径') plt.show()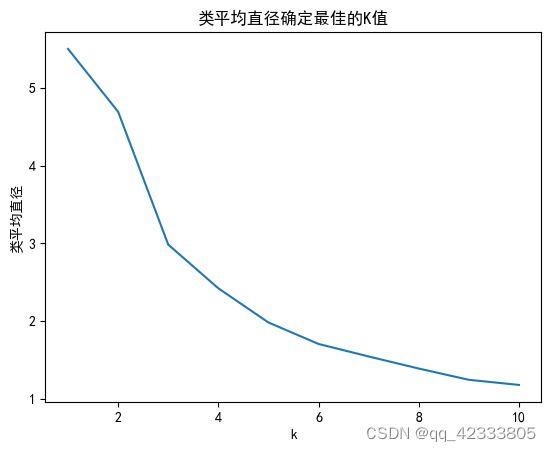
从这个图看转折点大概在5。
3.2聚类
故综合看选择k=5。进行聚类,聚类后查看每个类别的数量。
KM = KMeans(n_clusters=5, init='k-means++', max_iter=300, n_init=10, random_state=0).fit(data_Standard) data_Standard['KM_result']=KM.labels_ data_Standard.groupby('KM_result').size()
将聚类的结果可视化,从年收入和支出分数来看,能将样本很好的分开;其他变量有重合部分,说明类别之间有相似之处。
# 聚类结果可视化 colors = np.array(['red', 'green', 'blue', 'yellow', 'grey'])# ,'black','pink','lightgreen' from pandas.plotting import scatter_matrix scatter_matrix(data, s=100, alpha=1, c=colors[data_Standard['KM_result']], figsize=(10, 10))
比如年收入较低的一部分群体,可以大致按年龄分开,35岁以上(灰色点)分为了一类,35以下(黄色点)分成了一类;而35岁以下的对应的支出分数有很高,说明消费能力强;35岁以上的消费能力弱。
# 查看此时的轮廓系数 silhouette = silhouette_score(data_Standard.loc[:,~data_Standard.columns.isin(['KM_result'])], KM.labels_) print("轮廓系数", silhouette)此时轮廓系数 0.5546571631111091
3.3层次聚类找聚类中心
前面部分初始聚类中心的选择是选择距离最远的样本作为下一个类的质心,同样在李航《统计学习方法》中说到可以使用离层次聚类最近的点作为初始聚类中心,以下做一个尝试。

先利用层次聚类找到初始聚类中心,再进行kmeans聚类。
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster data_Standard_1=data_Standard[['Annual Income (k$)','Spending Score (1-100)']] linkage_matrix = linkage(data_Standard_1, method='ward') print("聚类过程:", linkage_matrix)fig = plt.figure(figsize=(15, 10)) # 将层级聚类结果以树状图表示出来 dn = dendrogram(linkage_matrix) plt.show()
以上是层次聚类的结果,接下来找离中心最近的点。
# 寻找离聚类中心最近的点 linkage_matrix = linkage(data_Standard_1, method='ward') # 确定类别数为5 num_clusters = 5 labels = fcluster(linkage_matrix, num_clusters, criterion='maxclust') # 计算每个簇的质心 unique_labels = np.unique(labels) centroids ={} for label in unique_labels: cluster_points = data_Standard_1[labels == label] centroid = cluster_points.mean().values centroids[label] = centroid # # 输出质心 # print("Cluster centroids:") # for i, centroid in enumerate(centroids): # print(f"Cluster {i+1}: {centroid}") # # 如果想要一个质心数组 # centroids = np.array(centroids) # 找出每个簇中距离中心最近的点 closest_points = {} for label, centroid in centroids.items(): distances = data_Standard_1.apply(lambda x: euclidean(x, centroid), axis=1) closest_index = distances.idxmin() closest_points[label] = data_Standard_1.loc[closest_index] closest_points=pd.DataFrame(closest_points).T closest_points
将离中心最近的点作为kmeans的初始点,再次进行聚类。
# 将层次聚类的聚类中心带入kmeans中进行聚类 KM1 = KMeans(n_clusters=5,init=closest_points).fit(data_Standard_1) data_Standard_1['KM_result']=KM1.labels_ data_Standard_1.groupby('KM_result').size()
silhouette = silhouette_score(data_Standard_1.loc[:,~data_Standard_1.columns.isin(['KM_result'])], KM1.labels_) print("轮廓系数", silhouette)轮廓系数 0.5546571631111091
看来就这个项目数据来说,使用层次聚类寻找初始聚类中心和使用kmeans++寻找初始中心,结果是一样的。
三、用户分群
通过前面的描述,已经将客户分为了五类,这里查看各类客户各变量的均值。
data['KM_result']=KM.labels_ data.groupby('KM_result').mean()| KM_result | Age | Annual Income (k$) | Spending Score (1-100) | Gender_encoded |
|---|---|---|---|---|
| 0 | 41.114286 | 88.200000 | 17.114286 | 0.457143 |
| 1 | 42.716049 | 55.296296 | 49.518519 | 0.592593 |
| 2 | 32.692308 | 86.538462 | 82.128205 | 0.538462 |
| 3 | 25.272727 | 25.727273 | 79.363636 | 0.590909 |
| 4 | 45.217391 | 26.304348 | 20.913043 | 0.608696 |

通过以上的分析,可以得出以下结论:
簇类0(红点): 这部分年龄在41岁左右,消费比较保守。他们高收入但消费行为低,可能有特定的偏好,导致他们在购物中心的消费较为保守。
簇类1(绿点): 这部分年龄在42岁左右,男性较多,具有中等收入和消费行为。他们既不是高消费群体,也不是低消费群体,表明了一种平衡的消费方式。
簇类2(蓝点):这部分代表了富裕的客户,他们有高收入,愿意慷慨消费。他们可能会优先考虑奢侈品和高端体验。
簇类3(黄点): 这一细分市场代表了收入相对较低但消费行为较高的年轻客户。他们可能是潮流的早期采用者,优先考虑体验式购买。
簇类4(灰点): 这部分是由低收入到中等收入和保守消费习惯的客户组成,平均年龄在所有类别中最大,男性为主,他们可能会优先购买必需品,对价格更加敏感。
参考:Mall Customer Segmentation - KMeans & Meanshift (kaggle.com)
