前言
在之前的文章介绍了定点数为什么需要舍入和几种常见的舍入模式。今天我们再来看看另外一种舍入模式:向上取整fix。
10进制数的fix
fix:也叫 向0取整。它的舍入方式是数据往0的方向,舍入到最近的整数,比如1.75 fix到2,-0.25 fix到0等。以-2到1.75之间的16个数据(步长0.25)为例,它们的 fix 结果是这样的:
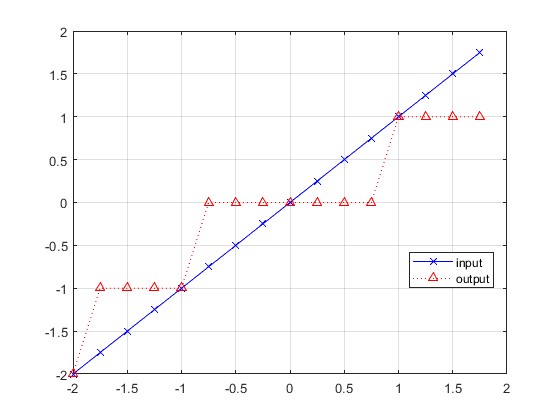
从上图可以看到:
正数的fix,就是把小数部分(或者约定精度外的部分)丢掉。例如1.5 >> 1,0.5 >> 0,1 >> 1 等
负数的fix,也是把小数部分(或者约定精度外的部分)丢掉。例如-1.5 >> -1,-0.5 >> 0,-1 >> -1 等
0的fix,同样是直接丢掉小数部分
2进制数的fix
2进制数的fix和10进制的fix类似,但是对于负数部分的处理是不同的。以Q4.2格式的定点数(字长4位,小数2位的有符号数)为例,对于负数的小数部分的处理:
-2(d) = 10_00(b) fix后的值为 -2,等价于 10,即舍弃小数部分的值(10)
-1.75(d) = 10_01(b) fix后的值为 -1,等价于 11,即舍弃小数部分的值(10)后再加1
-1.5(d) = 10_10(b) fix后的值为 -1,等价于 11,即舍弃小数部分的值(10)后再加1
-1.25(d) = 10_11(b) fix后的值为 -1,等价于 11,即舍弃小数部分的值(10)后再加1
-1(d) = 11_00(b) fix后的值为 -1,等价于 11,即舍弃小数部分
-0.75(d) = 11_01(b) fix后的值为 0,等价于 00,即舍弃小数部分的值(10)后再加1
-0.5(d) = 11_10(b) fix后的值为 0,等价于 00,即舍弃小数部分的值(10)后再加1
-0.25(d) = 11_11(b) fix后的值为 0,等价于 00,即舍弃小数部分的值(10)后再加1
总结一下,就是:
小数部分不为0时就是把小数部分(或者约定精度外的部分)丢掉再加1。
小数部分为0时就是把小数部分(或者约定精度外的部分)丢掉。
对于正数和0的处理和10进制的方式相同,都是:
直接把小数部分(或者约定精度外的部分)丢掉,例如1.25即01_01 fix的结果是1即01,0.75即00_11 fix的结果是0即00
从上面可以看出来,fix对于正数来说相当于向下取整floor,对于负数来说相当于向上取整ceil。因此,fix的实现可以简化为:
首先舍去小数部分,然后剩余整数部分加上一个进位。当该数是为负的非整数时,进位为1;否则进位为0。
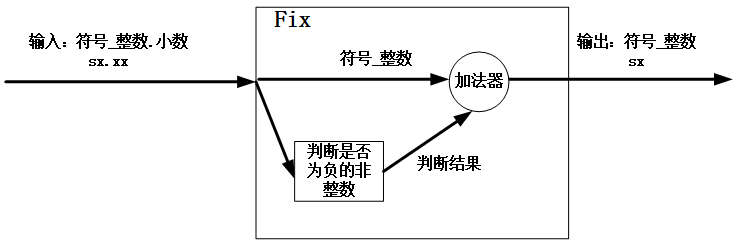
下面以 用fix的方式来实现Q4.2格式定点数转Q2.0格式定点数为例,Verilog代码如下:
module test( input [3:0] data_4Q2, //有符号数,符号1位,字长4位,小数2位 output [1:0] data_2Q0 //有符号数,符号1位,字长2位,小数0位 ); wire carry; assign carry = data_4Q2[3] && (|data_4Q2[1:0]); //是负数且非整数时进位为1,其他进位为0 assign data_2Q0 = data_4Q2[3:2] + carry; //舍弃低位(即整个小数部分)后再加进位 endmodule因为一共只有16个数,所以我们可以用穷举的方式来测试,TB如下:
`timescale 1ns/1ns module test_tb(); reg [3:0] data_4Q2; //有符号数,符号1位,整数2位,小数2位 wire [1:0] data_2Q0; //有符号数,符号1位,整数2位,小数0位 integer i; //循环变量 initial begin data_4Q2 = 0; //输入赋初值 for(i=0;i<16;i=i+1)begin //遍历所有的输入,共16个 data_4Q2 = i; #5; $display("data_4Q2:%h data_2Q0:%h",data_4Q2,data_2Q0); end #20 $stop(); //结束仿真 end //例化被测试模块 test test_inst( .data_4Q2 (data_4Q2), .data_2Q0 (data_2Q0) ); endmodule同时,我们也用matlab来实现同样的功能,观察两者的输出是否一致:
%-------------------------------------------------- % 关闭无关内容 clear; close all; clc; %-------------------------------------------------- % 生成数据并做fix处理 x = -2:0.25:1.75; F = fimath('RoundingMethod','Zero'); % 设定舍入模式为fix data_4Q2 = fi(x,1,4,2,F); % 生成Q4.2格式的定点数 data_2Q0 = fi(data_4Q2,1,2,0,F); % 从Q4.2格式转换成Q2.0格式 % 打印数据 for i=1:length(data_4Q2) fprintf('data_4Q2:%s data_2Q0:%s\n',hex(data_4Q2(i)),hex(data_2Q0(i))) end下图是2者分别输出的数据(16进制),可以看到数据的输出是一致的,证明RTL代码无误。
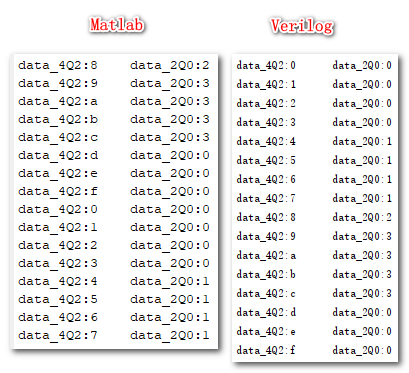
这几个数的输入分别是0101/0110/0111,即10进制数1.25/1.5/1.75,它们fix结果应该是2。从上图来看,好像是matlab错了,而RTL对了,但实际情况恰恰相反。现在想想结果是什么格式的?Q2.0!它能表示的最大的数是多少?是10进制的1!所以结果溢出了!
那为什么RTL的结果又 ”对“ 了呢?这纯属是乌龙。因为打印结果是16进制的,并不表示10进制数值,结合结果的2位位宽,可知 ”2“,实际上就是10,它是01的溢出产生的,这个数在Q2.0格式的定点数中并不表示 ”数字2“,而是数字 ”-1“。
matlab是有溢出处理机制的(saturate),它把溢出值把都饱和在了最大值即01(10进制的1)。为了防止这种情况的发生,我们也要设计对应的溢出处理机制。因为是向上取整,所以结果只会是正向的溢出,那么就只要限定最大值即可,把Verilog代码改一下:
module test( input [3:0] data_4Q2, //有符号数,符号1位,字长4位,小数2位 output [1:0] data_2Q0 //有符号数,符号1位,字长2位,小数0位 ); wire carry; wire [2:0] data_temp; //扩展1bit,防止溢出 assign carry = |data_4Q2[1:0]; //是整数时进位为0,非整数进位为1 assign data_temp = {data_4Q2[3],data_4Q2[3:2]} + {2'b00,carry}; //中间变量,舍弃低位(即整个小数部分)后再加进位 assign data_2Q0 = (data_temp[2:1]==2'b01) ? 2'b01 : data_temp[1:0]; //data_2Q0的高2位为01说明产生了正向的进位,即溢出 endmodule非整数的ceil,相当于先丢小数部分,然后把剩余的整数部分+1:
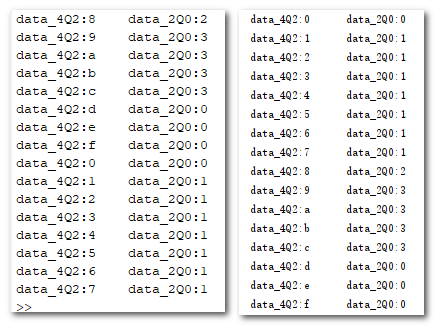
定点数从Q4.2格式转Q2.0格式是一个比较特殊的例子,因为它相当于把小数部分全部舍弃掉了,如果舍入要求不是全部小数位,而是部分小数位,那么处理方式是一样的吗?
是一样的。对于其他情况则只需要把精度要求外的小数部分舍弃即可。例如Q5.3格式的定点数转Q3.1格式,则只需要把最后两位小数舍弃即可,例如:
00.111 是0.875,fix到向0方向即向下方向距离它最近的Q3.1格式的数是0.5即00.1,即00.111 >> 00.1。操作上相当于上面说的舍弃掉多余的小数位
10.111 是-1.125,fix到向0方向即向上方向距离它最近的Q3.1格式的数是-1即11.0,即10.111 >> 10.1 + 1 >> 11.0。操作上相当于上面说的舍弃掉多余的小数位,然后加1。
其他类似,不赘述了。
