案例背景
又要开始更新时间序列水论文的系列的方法了,前面基于各种不同神经网络层,还有注意力机制做了一些缝合模型。
其实论文里面用的多的可能是优化算法和模态分解,这两个我还没出专门的例子,这几天正好出一个优化算法的例子来做一个时间序列模型的缝合版。
想看更多的发论文用的模型可以参考我数据分析案例之前的文章,或者关注我后面的文章。
其实优化算法在python里面的生态不如MATLAB,现有的包很少,所以都是现写的。我自己也有优化算法专栏,以后有机会都写上去。本次的Python版的麻雀算法就是手写的,网上基本没有。
本次就简单点,使用优化算法里面表现较好的麻雀优化算法,优化算法我也做过一些测试,虽然都是各有优势,但是从通用性和整体表现来看,麻雀优化算法表现是较好的,那些什么混沌麻雀,自适应麻雀也差不多,可能在特殊的情况下表现会好一些。什么,你问问为什么不用粒子群,退火,遗传这种算法?emmmm,你自己去找些函数试试就知道他们比麻雀算法差多少了。。。
数据介绍
本次数据集有两个csv,一个桥面风速,一个气象站风速。
 ,
,
一般来说,桥面风速是好测量的,气象站的风速是被认为是真实的风速,所以我们当前的用气象站的风速作为y,之前的桥面风速和气象站风速作为X。
当然,需要本次案例演示数据和全部代码文件的同学还是可以参考:风速预测。
代码实现
导入包,深度学习的包有点多、
import os import math import time import datetime import random as rn import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline plt.rcParams ['font.sans-serif'] ='SimHei' #显示中文 plt.rcParams ['axes.unicode_minus']=False #显示负号 from sklearn.model_selection import train_test_split from sklearn.preprocessing import MinMaxScaler,StandardScaler from sklearn.metrics import mean_absolute_error from sklearn.metrics import mean_squared_error,r2_score import tensorflow as tf import keras from keras.layers import Layer import keras.backend as K from keras.models import Model, Sequential from keras.layers import GRU, Dense,Conv1D, MaxPooling1D,GlobalMaxPooling1D,Embedding,Dropout,Flatten,SimpleRNN,LSTM from keras.callbacks import EarlyStopping #from tensorflow.keras import regularizers #from keras.utils.np_utils import to_categorical from tensorflow.keras import optimizers读取数据,展示前五行
data0=pd.concat([pd.read_excel('bridge2.xlsx').set_index('时间'), pd.read_excel('weather_station.xlsx').set_index('时间')],axis=1).sort_index().fillna(0) data0.head()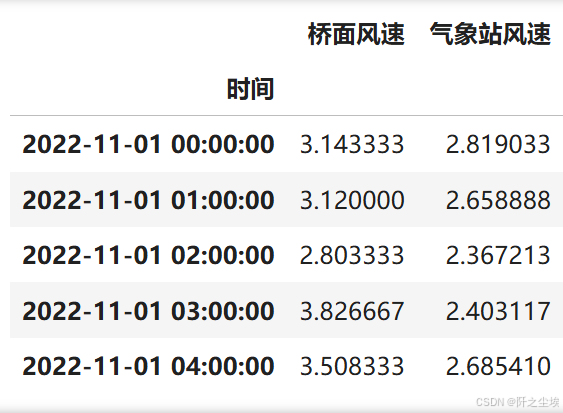
一行代码读取两个文件,并且合并,代码风格还是简洁优雅的。
注意想换成自己的数据集的话,要预测的y放在最后一列。
构建训练集和测试集
时间序列的预测一套滑动窗口,构建的函数如下
def build_sequences(text, window_size=24): #text:list of capacity x, y = [],[] for i in range(len(text) - window_size): sequence = text[i:i+window_size] target = text[i+window_size] x.append(sequence) y.append(target) return np.array(x), np.array(y) def get_traintest(data,train_ratio=0.8,window_size=24): train_size=int(len(data)*train_ratio) train=data[:train_size] test=data[train_size-window_size:] X_train,y_train=build_sequences(train,window_size=window_size) X_test,y_test=build_sequences(test,window_size=window_size) return X_train,y_train[:,-1],X_test,y_test[:,-1]对x和y进行标准化
data=data0.to_numpy() scaler = MinMaxScaler() scaler = scaler.fit(data[:,:-1]) X=scaler.transform(data[:,:-1]) y_scaler = MinMaxScaler() y_scaler = y_scaler.fit(data[:,-1].reshape(-1,1)) y=y_scaler.transform(data[:,-1].reshape(-1,1))划分训练集和测试集
train_ratio=0.8 #训练集比例 window_size=64 #滑动窗口大小,即循环神经网络的时间步长 X_train,y_train,X_test,y_test=get_traintest(np.c_[X,y],window_size=window_size,train_ratio=train_ratio) print(X_train.shape,y_train.shape,X_test.shape,y_test.shape)
数据可视化
y_test = y_scaler.inverse_transform(y_test.reshape(-1,1)) test_size=int(len(data)*(1-train_ratio)) plt.figure(figsize=(10,5),dpi=256) plt.plot(data0.index[:-test_size],data0.iloc[:,-1].iloc[:-test_size],label='Train',color='#FA9905') plt.plot(data0.index[-test_size:],data0.iloc[:,-1].iloc[-(test_size):],label='Test',color='#FB8498',linestyle='dashed') plt.legend() plt.ylabel('Predict Series',fontsize=16) plt.xlabel('Time',fontsize=16) plt.show()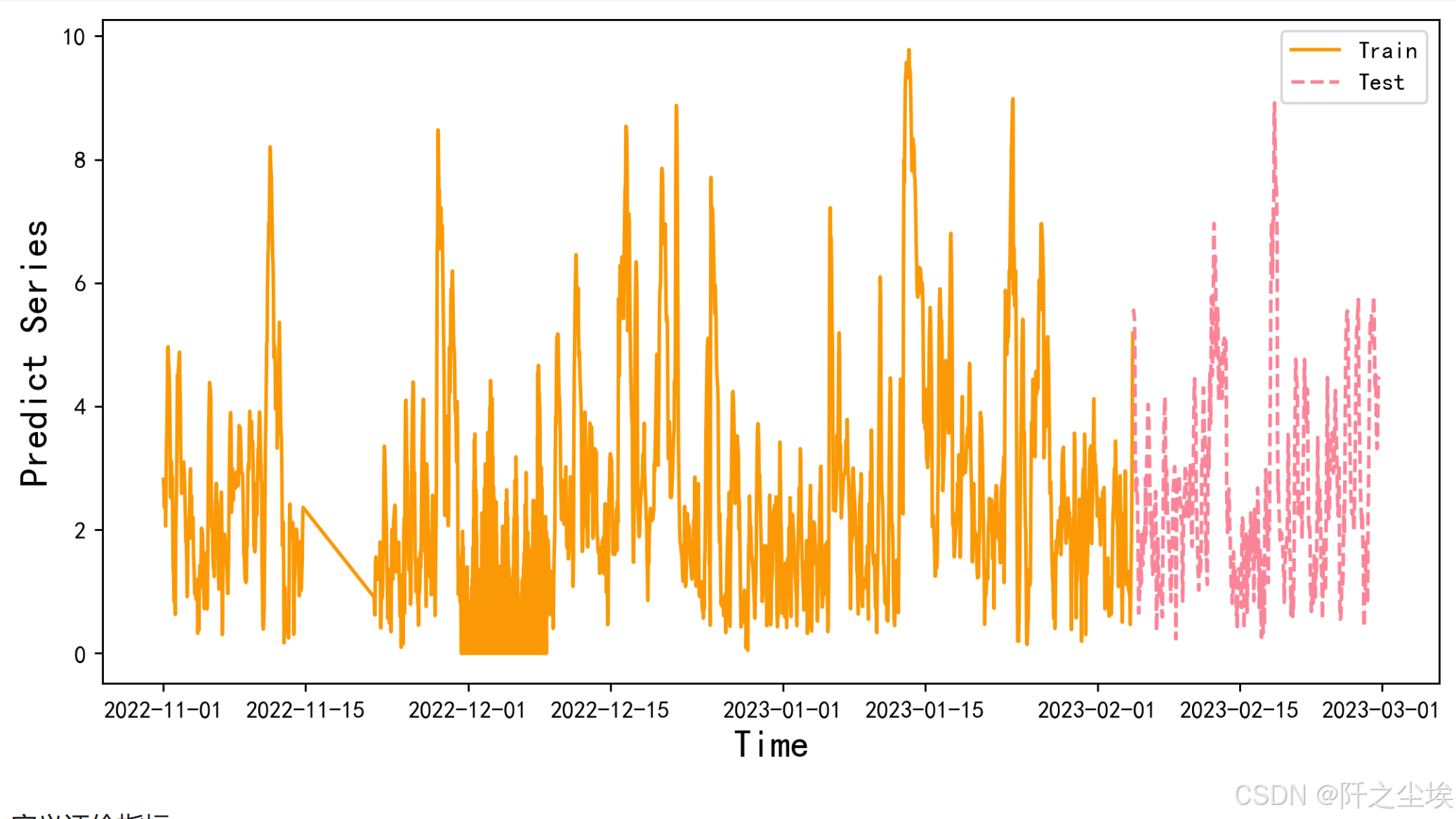
训练函数的准备
下面继续自定义函数,评价指标
def set_my_seed(): os.environ['PYTHONHASHSEED'] = '0' np.random.seed(1) rn.seed(12345) tf.random.set_seed(123) def evaluation(y_test, y_predict): mae = mean_absolute_error(y_test, y_predict) mse = mean_squared_error(y_test, y_predict) rmse = np.sqrt(mean_squared_error(y_test, y_predict)) mape=(abs(y_predict -y_test)/ y_test).mean() #r_2=r2_score(y_test, y_predict) return mse, rmse, mae, mape #r_2我们使用回归问题常用的mse, rmse, mae, mape作为预测效果的评价指标。
自定义注意力机制的类
class AttentionLayer(Layer): #自定义注意力层 def __init__(self, **kwargs): super(AttentionLayer, self).__init__(**kwargs) def build(self, input_shape): self.W = self.add_weight(name='attention_weight', shape=(input_shape[-1], input_shape[-1]), initializer='random_normal', trainable=True) self.b = self.add_weight(name='attention_bias', shape=(input_shape[1], input_shape[-1]), initializer='zeros', trainable=True) super(AttentionLayer, self).build(input_shape) def call(self, x): # Applying a simpler attention mechanism e = K.tanh(K.dot(x, self.W) + self.b) a = K.softmax(e, axis=1) output = x * a return output def compute_output_shape(self, input_shape): return input_shape自定义模型的构建
def build_model(X_train,mode='LSTM',hidden_dim=[32,16]): set_my_seed() model = Sequential() if mode=='MLP': model.add(Dense(hidden_dim[0],activation='relu',input_shape=(X_train.shape[-2],X_train.shape[-1]))) model.add(Flatten()) model.add(Dense(hidden_dim[1],activation='relu')) elif mode=='LSTM': # LSTM model.add(LSTM(hidden_dim[0],return_sequences=True, input_shape=(X_train.shape[-2],X_train.shape[-1])))# model.add(LSTM(hidden_dim[1])) #model.add(Flatten()) #model.add(Dense(hidden_dim[1], activation='relu')) elif mode=='GRU': #GRU model.add(GRU(hidden_dim[0],return_sequences=True, input_shape=(X_train.shape[-2],X_train.shape[-1]))) model.add(GRU(hidden_dim[1])) elif mode == 'Attention-LSTM': model.add(LSTM(hidden_dim[0], return_sequences=True, input_shape=(X_train.shape[-2], X_train.shape[-1]))) model.add(AttentionLayer()) #model.add(LSTM(hidden_dim[1]))#, return_sequences=False model.add(Flatten()) model.add(Dense(hidden_dim[1], activation='relu')) #model.add(Dense(4, activation='relu')) elif mode=='SSA-LSTM': # LSTM model.add(LSTM(hidden_dim[0],input_shape=(X_train.shape[-2],X_train.shape[-1])))#return_sequences=True, model.add(Dense(hidden_dim[1], activation='relu')) model.add(Dense(1)) model.compile(optimizer='Adam', loss='mse',metrics=[tf.keras.metrics.RootMeanSquaredError(),"mape","mae"]) return model 自定义画损失图函数和预测对比函数
def plot_loss(hist,imfname=''): plt.subplots(1,4,figsize=(16,2)) for i,key in enumerate(hist.history.keys()): n=int(str('14')+str(i+1)) plt.subplot(n) plt.plot(hist.history[key], 'k', label=f'Training {key}') plt.title(f'{imfname} Training {key}') plt.xlabel('Epochs') plt.ylabel(key) plt.legend() plt.tight_layout() plt.show() def plot_fit(y_test, y_pred): plt.figure(figsize=(4,2)) plt.plot(y_test, color="red", label="actual") plt.plot(y_pred, color="blue", label="predict") plt.title(f"拟合值和真实值对比") plt.xlabel("Time") plt.ylabel('power') plt.legend() plt.show()可能有的小伙伴觉得看不懂了,没关系,我都是高度的封装,不需要知道每个函数里面的细节,大概知道他们是做什么的就行。因为下面要把他们全部打包为训练函数,改一下参数就可以使用不同的模型,很方便,
df_eval_all=pd.DataFrame(columns=['MSE','RMSE','MAE','MAPE']) df_preds_all=pd.DataFrame() def train_fuc(mode='LSTM',batch_size=64,epochs=30,hidden_dim=[32,16],verbose=0,show_loss=True,show_fit=True): #构建模型 s = time.time() set_my_seed() model=build_model(X_train=X_train,mode=mode,hidden_dim=hidden_dim) earlystop = EarlyStopping(monitor='loss', min_delta=0, patience=5) hist=model.fit(X_train, y_train,batch_size=batch_size,epochs=epochs,callbacks=[earlystop],verbose=verbose) if show_loss: plot_loss(hist) #预测 y_pred = model.predict(X_test) y_pred = y_scaler.inverse_transform(y_pred) #print(f'真实y的形状:{y_test.shape},预测y的形状:{y_pred.shape}') if show_fit: plot_fit(y_test, y_pred) e=time.time() print(f"运行时间为{round(e-s,3)}") df_preds_all[mode]=y_pred.reshape(-1,) s=list(evaluation(y_test, y_pred)) df_eval_all.loc[f'{mode}',:]=s s=[round(i,3) for i in s] print(f'{mode}的预测效果为:MSE:{s[0]},RMSE:{s[1]},MAE:{s[2]},MAPE:{s[3]}') print("=======================================运行结束==========================================") return s[0]所有的函数都准备完了,下面初始化参数,开始准备训练模型
window_size=64 batch_size=64 epochs=30 hidden_dim=[32,16] verbose=0 show_fit=True show_loss=True mode='LSTM' #MLP,GRUMLP模型训练
train_fuc(mode='MLP',batch_size=batch_size,epochs=epochs,hidden_dim=hidden_dim,verbose=1)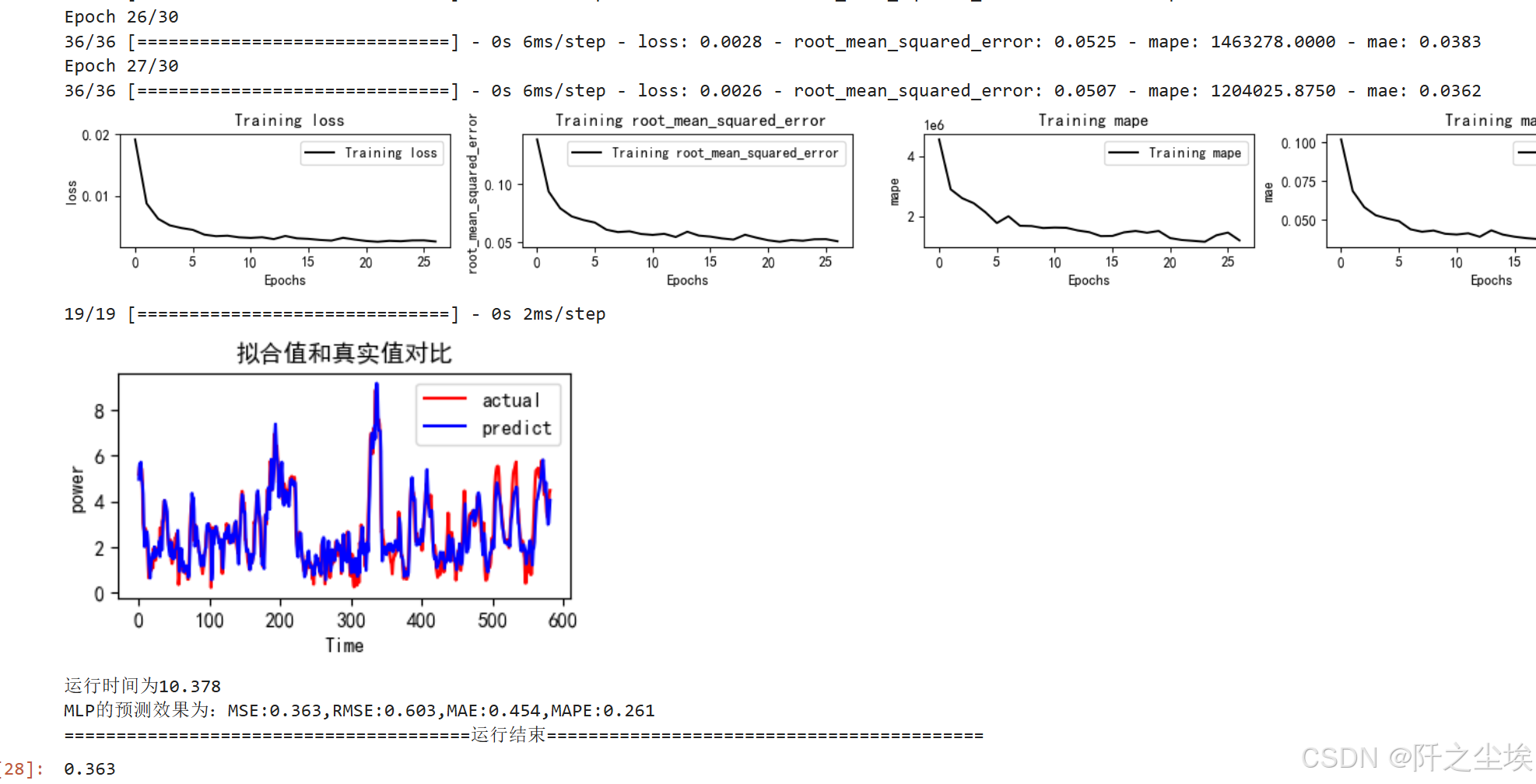
可以看到这个训练函数运行完后,可以清晰的看到每个训练轮的损失,损失的变化图,预测的效果对比图,还有评价指标的计算结果。
换模型也很便捷,只需要该mode这一个参数就行。
GRU模型训练
修改一下mode就行,其他参数你可以改也可以不改
train_fuc(mode='GRU',batch_size=batch_size,epochs=epochs,hidden_dim=hidden_dim,verbose=1)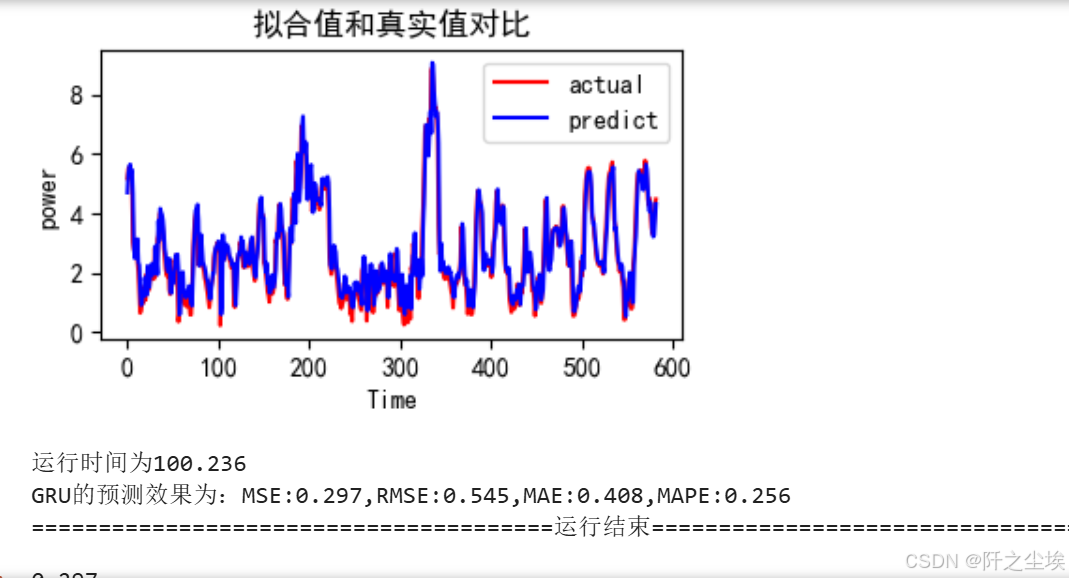
LSTM训练
train_fuc(mode='LSTM',batch_size=batch_size,epochs=epochs,hidden_dim=hidden_dim,verbose=1)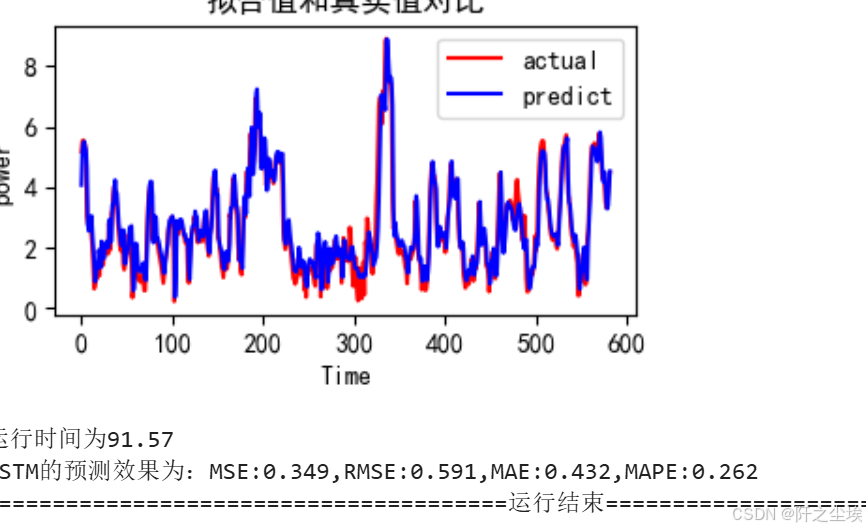
Attention-LSTM模型的训练
train_fuc(mode='Attention-LSTM',batch_size=batch_size,epochs=epochs,hidden_dim=hidden_dim,verbose=1)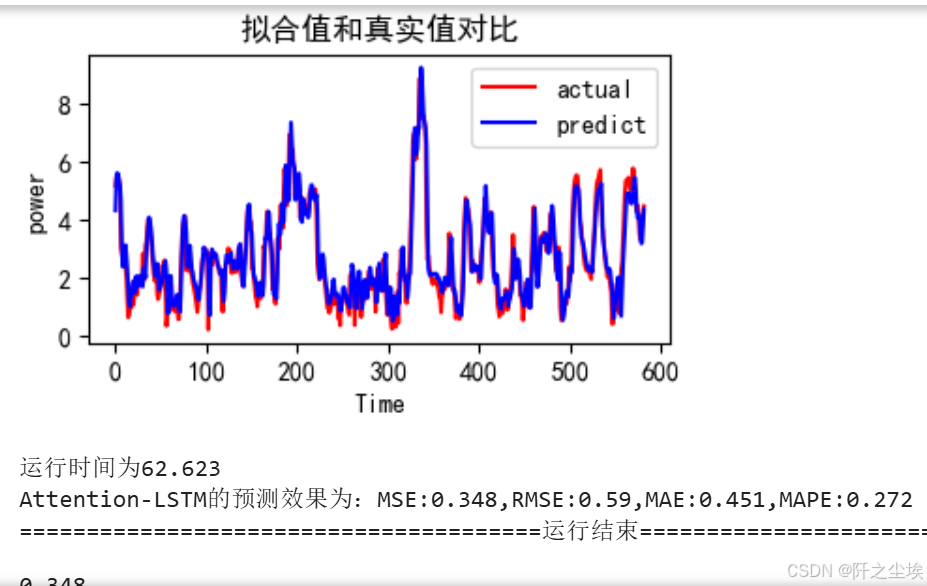
好像加了注意力机制的效果只变好了一点点。
麻雀搜索优化算法(SSA)
这里直接写上SSA的源代码,python版本的网上几乎是没有的
import numpy as np import random import copy from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D ''' 种群初始化函数 ''' def initial(pop, dim, ub, lb): X = np.zeros([pop, dim]) for i in range(pop): for j in range(dim): X[i, j] = random.random()*(ub[j] - lb[j]) + lb[j] return X,lb,ub '''边界检查函数''' def BorderCheck(X,ub,lb,pop,dim): for i in range(pop): for j in range(dim): if X[i,j]>ub[j]: X[i,j] = ub[j] elif X[i,j]<lb[j]: X[i,j] = lb[j] return X '''计算适应度函数''' def CaculateFitness(X,fun): pop = X.shape[0] fitness = np.zeros([pop, 1]) for i in range(pop): fitness[i] = fun(X[i, :]) return fitness '''适应度排序''' def SortFitness(Fit): fitness = np.sort(Fit, axis=0) index = np.argsort(Fit, axis=0) return fitness,index '''根据适应度对位置进行排序''' def SortPosition(X,index): Xnew = np.zeros(X.shape) for i in range(X.shape[0]): Xnew[i,:] = X[index[i],:] return Xnew '''麻雀发现者更新''' def PDUpdate(X,PDNumber,ST,Max_iter,dim): X_new = copy.copy(X) R2 = random.random() for j in range(PDNumber): if R2<ST: X_new[j,:] = X[j,:]*np.exp(-j/(np.random.random()*Max_iter)) else: X_new[j,:] = X[j,:] + np.random.randn()*np.ones([1,dim]) return X_new '''麻雀加入者更新''' def JDUpdate(X,PDNumber,pop,dim): X_new = copy.copy(X) for j in range(PDNumber+1,pop): if j>(pop - PDNumber)/2 + PDNumber: X_new[j,:]= np.random.randn()*np.exp((X[-1,:] - X[j,:])/j**2) else: #产生-1,1的随机数 A = np.ones([dim,1]) for a in range(dim): if(random.random()>0.5): A[a]=-1 AA = np.dot(A,np.linalg.inv(np.dot(A.T,A))) X_new[j,:]= X[1,:] + np.abs(X[j,:] - X[1,:])*AA.T return X_new '''危险更新''' def SDUpdate(X,pop,SDNumber,fitness,BestF): X_new = copy.copy(X) Temp = range(pop) RandIndex = random.sample(Temp, pop) SDchooseIndex = RandIndex[0:SDNumber] for j in range(SDNumber): if fitness[SDchooseIndex[j]]>BestF: X_new[SDchooseIndex[j],:] = X[0,:] + np.random.randn()*np.abs(X[SDchooseIndex[j],:] - X[1,:]) elif fitness[SDchooseIndex[j]] == BestF: K = 2*random.random() - 1 X_new[SDchooseIndex[j],:] = X[SDchooseIndex[j],:] + K*(np.abs( X[SDchooseIndex[j],:] - X[-1,:])/(fitness[SDchooseIndex[j]] - fitness[-1] + 10E-8)) return X_new '''麻雀搜索算法''' def SSA(pop,dim,lb,ub,Max_iter,fun): ST = 0.6 #预警值 PD = 0.7 #发现者的比列,剩下的是加入者 SD = 0.2 #意识到有危险麻雀的比重 PDNumber = int(pop*PD) #发现者数量 SDNumber = int(pop*SD) #意识到有危险麻雀数量 X,lb,ub = initial(pop, dim, ub, lb) #初始化种群 fitness = CaculateFitness(X,fun) #计算适应度值 fitness,sortIndex = SortFitness(fitness) #对适应度值排序 X = SortPosition(X,sortIndex) #种群排序 GbestScore = copy.copy(fitness[0]) GbestPositon = np.zeros([1,dim]) GbestPositon[0,:] = copy.copy(X[0,:]) Curve = np.zeros([Max_iter,1]) for i in range(Max_iter): BestF = fitness[0] X = PDUpdate(X,PDNumber,ST,Max_iter,dim)#发现者更新 X = JDUpdate(X,PDNumber,pop,dim) #加入者更新 X = SDUpdate(X,pop,SDNumber,fitness,BestF) #危险更新 X = BorderCheck(X,ub,lb,pop,dim) #边界检测 fitness = CaculateFitness(X,fun) #计算适应度值 fitness,sortIndex = SortFitness(fitness) #对适应度值排序 X = SortPosition(X,sortIndex) #种群排序 if(fitness[0]<=GbestScore): #更新全局最优 GbestScore = copy.copy(fitness[0]) GbestPositon[0,:] = copy.copy(X[0,:]) Curve[i] = GbestScore return GbestScore,GbestPositon,Curve这个模块可以写外面,从工程的角度来看放在一个py里面导入是最合理的。但是我们这是案例,考虑到简洁和易学性,所以我们都放在一个文件里面了。
优化算法定义完成后,定义目标函数
#import SSA def fobj(X): s=train_fuc(mode='SSA-LSTM',batch_size=int(X[0]),epochs=int(X[1]),hidden_dim=[int(X[2]),int(X[3])],verbose=0,show_loss=False,show_fit=False) return s进行优化算法的训练:
GbestScore1,GbestPositon1,Curve1 = SSA(pop=2,dim=4,lb=[8,20,30,12],ub=[40,40,80,42],Max_iter=2,fun=fobj) 
我这里由于时间问题,我种群数量pop只用了2个,一般是30个,迭代次数一般是100-200次,我就改了2次,因为新电脑的TensorFlow不支持GPU加速,算的太慢了.......就没去搜索那么多次,就填了个较小的数字做演示好了。
打印最优的参数解和最优的适应度值
print('最优适应度值:',GbestScore1) GbestPositon1=[int(i)for i in GbestPositon1[0]] print('最优解为:',GbestPositon1)带入最优解:
train_fuc(mode='SSA-LSTM',batch_size=GbestPositon1[0],epochs=GbestPositon1[1], hidden_dim=[GbestPositon1[2],GbestPositon1[3]],show_loss=True,show_fit=True,verbose=1)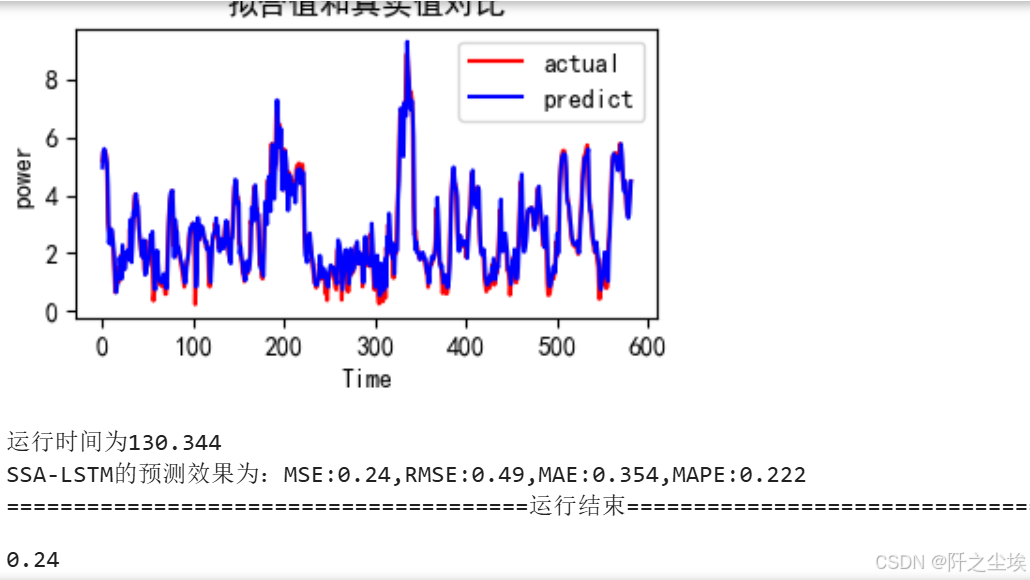
虽然没搜索几次,但是这个效果还是不错的。
查看评价指标对比
好了,所有的模型都训练和预测了,评价指标都算完了,我们当然想对比了,我前面写训练函数都已经留了一手,预测的结果和效果都存下来 了,和我一样一步步运行下来的可以直接查看预测效果。
df_eval_all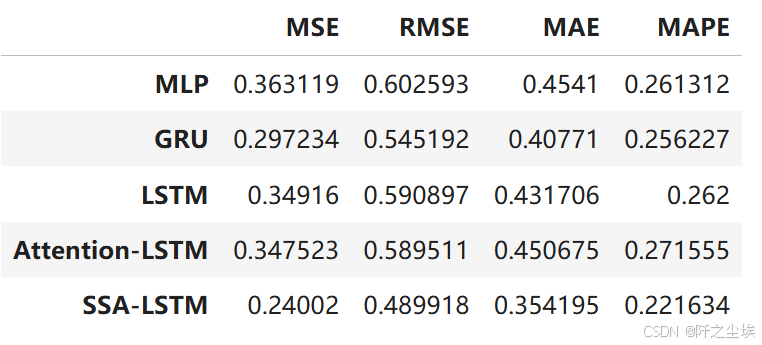
还是不直观,画图吧
bar_width = 0.4 colors=['c', 'orange','g', 'tomato','b', 'm', 'y', 'lime', 'k','orange','pink','grey','tan'] fig, ax = plt.subplots(2,2,figsize=(8,6),dpi=128) for i,col in enumerate(df_eval_all.columns): n=int(str('22')+str(i+1)) plt.subplot(n) df_col=df_eval_all[col] m =np.arange(len(df_col)) plt.bar(x=m,height=df_col.to_numpy(),width=bar_width,color=colors)# #plt.xlabel('Methods',fontsize=12) names=df_col.index plt.xticks(range(len(df_col)),names,fontsize=10) plt.xticks(rotation=40) plt.ylabel(col,fontsize=14) plt.tight_layout() #plt.savefig('柱状图.jpg',dpi=512) plt.show()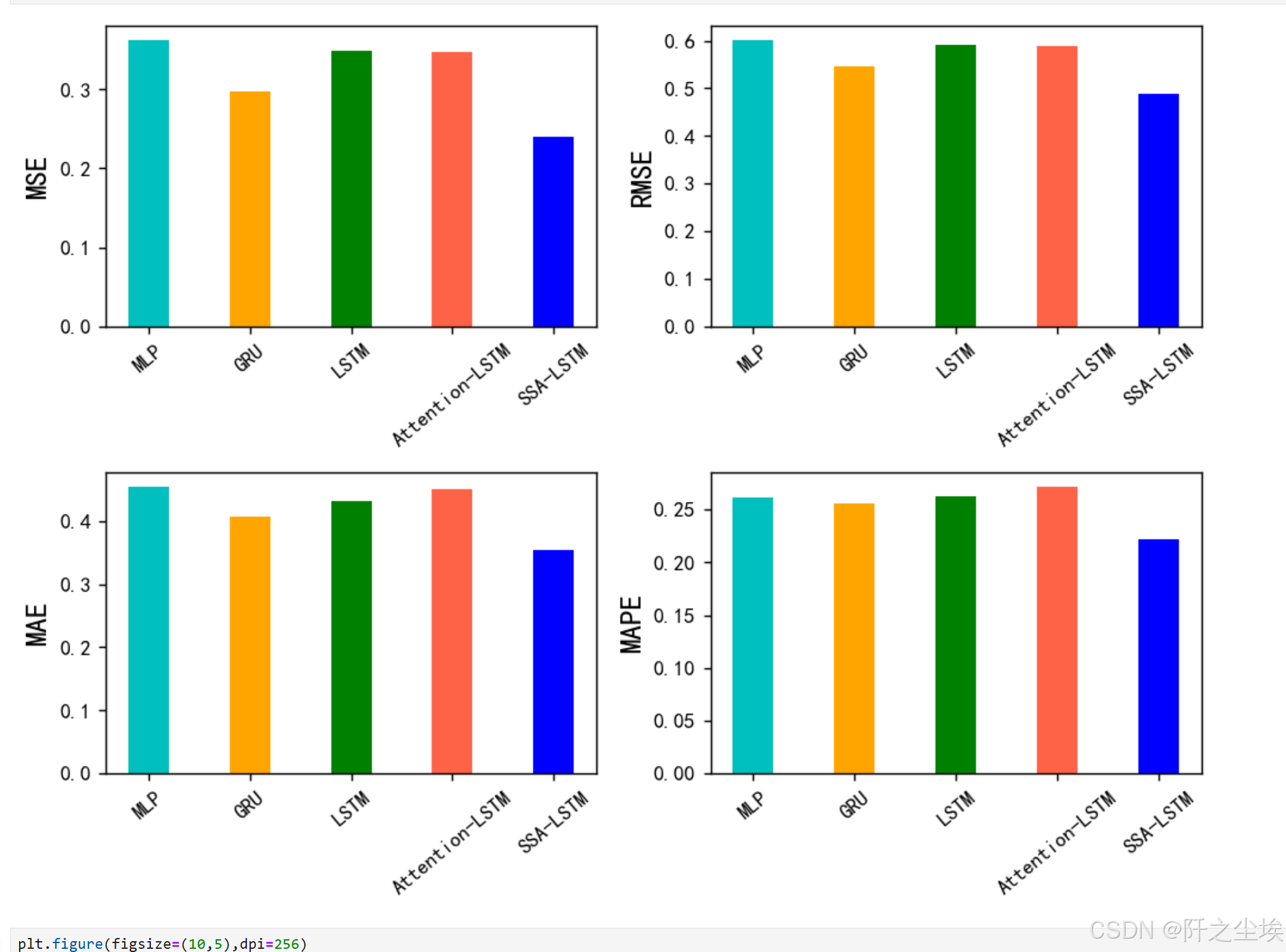
可以清楚地看见,SSA-lstm的效果最好,其次是GRU,然后是LSTM和attention-lstm。
所以说优化算法还是有效的,
继续画图他们的预测效果对比图:
plt.figure(figsize=(10,5),dpi=256) for i,col in enumerate(df_preds_all[['MLP','GRU','LSTM','Attention-LSTM','SSA-LSTM']].columns): plt.plot(data0.index[-test_size-1:],df_preds_all[col],label=col) # ,color=colors[i] plt.plot(data0.index[-test_size-1:],y_test.reshape(-1,),label='Actual',color='k',linestyle=':',lw=2) plt.legend() plt.ylabel('wind',fontsize=16) plt.xlabel('Date',fontsize=16) #plt.savefig('点估计线对比.jpg',dpi=256) plt.show()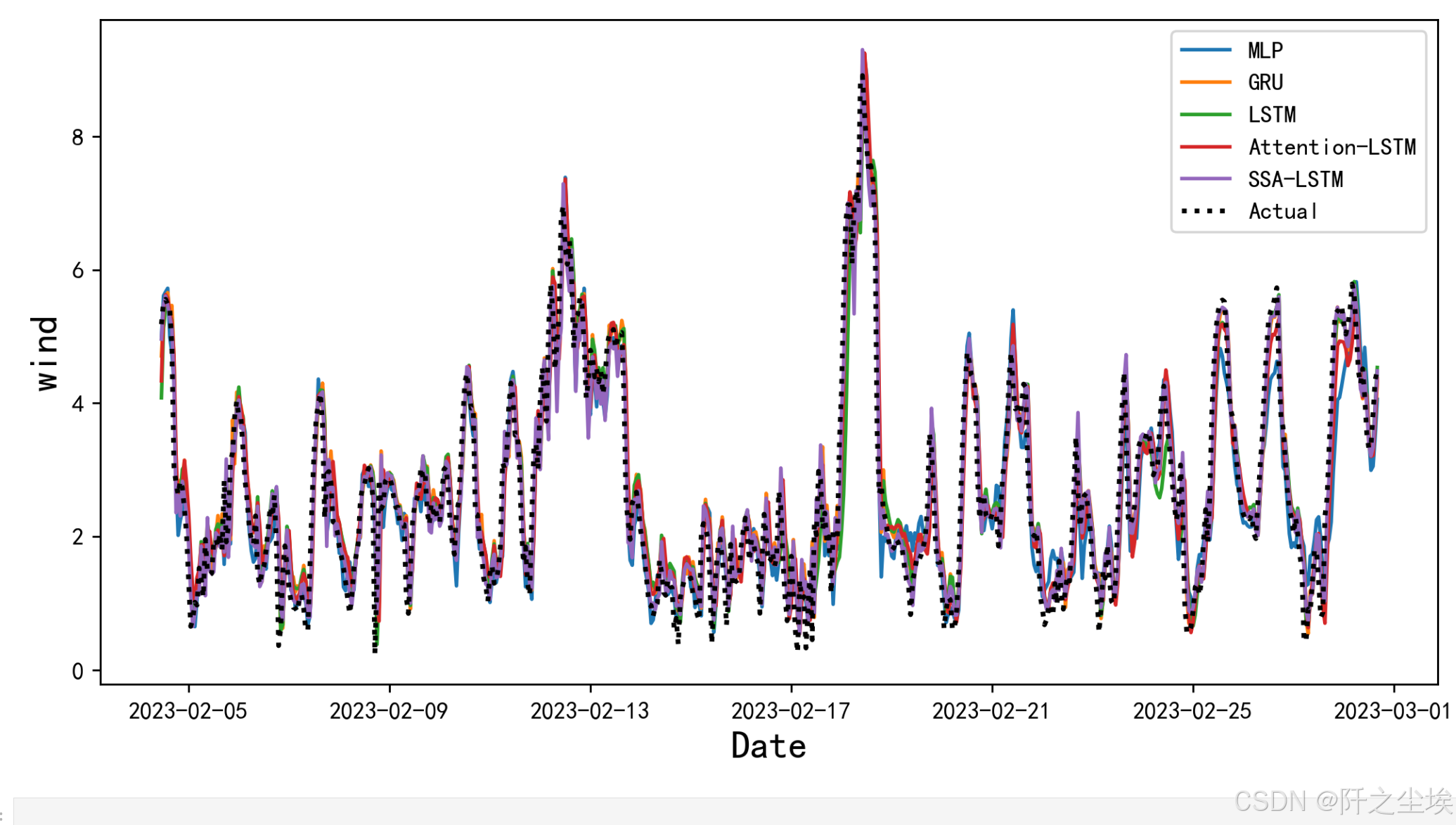
也可以从这个图清楚的看到预测效果对比
总结
在这个案例里面的,SSA-LSTM效果好于GRU好于LSTM和attention-LSTM,说明优化算的效果是可以的,当然同学们还有时间可以用SSA-GRU,SSA-attention-LSTM都去试试,,看谁的效果好。模型修改就该buildmodel这个函数,很简单的,搭积木,要什么层就写什么层的名字就行。
画个数据也是很容易实验的。
这是优化算法+神经网络的方法啦, 修改不同的优化算法就用自己自定义的算法替换就行,我后面的优化算法的专栏可能也会更新的,最近也有粉丝问问能不能出一个VMD或者CEEMDAN这些模态分解的对比,有时间我都写出来,可以关注我后面的文章。
创作不易,看官觉得写得还不错的话点个关注和赞吧,本人会持续更新python数据分析领域的代码文章~(需要定制类似的代码可私信)
