一、Affine Model Parameter
除了传统的平移运动补偿,AV1 还支持仿射变换模型,将当前像素点 (x, y) 通过以下方式投影到参考帧中的预测像素点 (x', y').
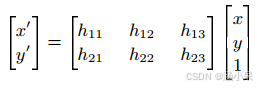
参数 (h13, h23) 对应于平移模型中使用的常规运动向量。 参数 h11 和 h22 控制垂直和水平轴上的比例因子,并与 h12 和 h21 一起决定旋转角度。
每个参考帧关联一个全局仿射模型,其中四个非平移参数的精度均为12位,平移运动矢量的编码精度为15位。一个编码块可以直接根据参考帧索引使用其仿射模型。
全局仿射模型捕获帧级缩放和旋转,主要关注整个帧的刚性运动设置。此外,编码块级别的仿射模型可以自适应地跟踪跨帧变化的非平移运动。然而,每个编码块发送仿射模型参数的开销成本也引入了额外的信息。因此,各种研究工作都集中在不增加额外开销的仿射模型参数估计上,AV1 采用一种基于空间相邻块的规则平移运动矢量的局部仿射参数估计方案。
编码块的局部仿射模型中的平移运动矢量 (h13, h23) 在比特流中显式传输。为了估计其他四个参数,假设局部尺度和旋转因子可以通过空间邻居的运动活动信息来反映。编解码器扫描编码块最近的相邻块,并根据运动信息使用和当前块相同参考帧的相邻块。最多允许八个相邻候选块。对于每个后选择的候选块,首先计算其中心位置和当前块中心位置的偏移,将该位置作为原始样本的位置,然后在该偏移的基础上,添加候选块和当前块间的运动矢量差,形成仿射变换后的目标样本的位置,对可用的原始和目标样本位置对进行最小二乘回归,计算仿射模型参数。
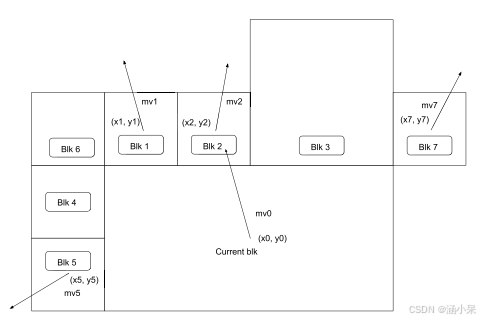
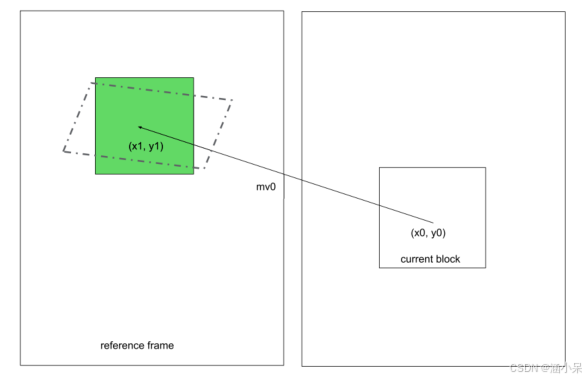
我们以上图为例来演示仿射参数估计过程。最近的相邻块由扫描顺序标记。对于Block k,其中心位置记为(xk, yk),运动矢量记为 mvk,其中当前编码块用 k = 0 表示。
假设,在这种情况下,相邻块 1、2、5和 7 与当前块使用相同的参考帧,选它们为参考块。原始样本位置形成为
![]()
式中k∈{1,2,5,7}。将运动矢量差进一步相加,得到相应的目标样本位置
![]()
为了构造最小二乘回归,我们将样本数据表示为
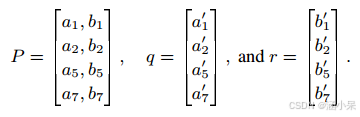
最小二乘回归计算出的 Affine 的参数为:
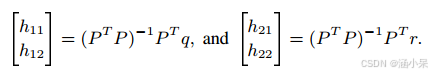
在实际中需要确保空间相邻块与当前块相关。因此,如果运动矢量差的任何分量的绝对值超过8个像素,我们就丢弃该参考块。此外,如果可用参考块的数量小于2,则最小二乘回归问题是病态的;因此,局部仿射模型被禁用。
二、Affine Motion Compensation
构建出 Affine 模型之后,进行Affine 模式的运动补偿。Affine 模型应用于 8x8 及以上的块大小。
一个预测块被分解成8 × 8个单元。首先由平移运动向量(h13, h23)确定每个 8×8 预测单元的中心像素,下图所示。下图中的绿色方格中位置(x, y)的其余像素,围绕中心像素(x1, y1)进行缩放和旋转,形成如下虚线中的仿射投影(x', y')
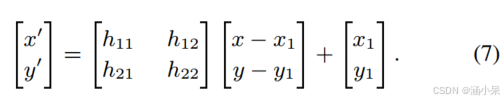
仿射投影允许 1/64 像素精度。设计了一组八抽头FIR滤波器(在某些情况下为六抽头)来进行亚像素插值。传统的平移模型在整个块上具有均匀的亚像素偏移量,这允许人们有效地“重用”大多数中间结果以减少总体计算。比如,要插值8 × 8块,首先应用水平滤波器从15 × 15 参考区域生成中间15 × 8数组。然后将垂直滤波器应用于中间的 15 × 8 数组,以产生最终的8 × 8预测块。因此,平移模型需要水平滤波进行(15×8)×8乘法运算,垂直滤波进行(8 × 8) × 8次乘法,共1472次乘法。
与平移模型不同,假设仿射模型中的每个像素由于旋转和缩放效应而具有不同的亚像素偏移是合理的。直接计算每个像素需要64 × 8 × 8 = 4096次乘法。然而,可以看到(7)中的旋转和缩放矩阵可以分解为两个剪切矩阵
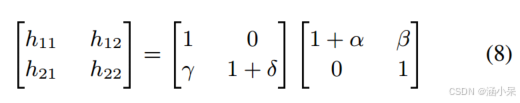
其中右边的第一项对应于垂直插值,第二项对应于水平插值。这将构建仿射参考块转换为两个阶段的插值操作。
首先通过在15 × 15参考区域上的水平滤波得到一个15 × 8 的中间数组,其中水平偏移量计算为
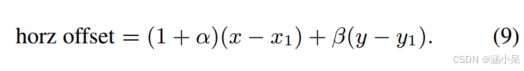
然后中间数组进行垂直滤波以插值垂直偏移量
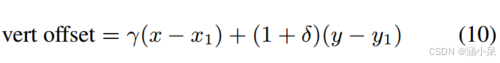
并生成8×8预测块。因此,它总共需要1472次乘法,与平移情况相同。然而,值得注意的是,仿射模型的实际计算成本仍然较高,因为每个像素的滤波系数都是变化的,而平移模型在水平和垂直方向分别使用固定的滤波器。
为了提高缓存性能,AV1要求 (9) 中的水平偏移量与 (x−x1) 的距离在1个像素以内,(10) 中的垂直偏移量与 (y−y1) 的距离在1个像素以内,这就限制了参考区域的距离在一个15×15像素数组内。考虑生成15 × 8中间像素数组的第一阶段。离其中心的位移为(x−x1)∈[−4,4],(y−y1)∈[−7,8]。
因此,我们对最大水平偏移量的约束为
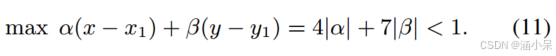
同样,在第二阶段(x−x1)∈[−4,4]和(y−y1)∈[−4,4],从而导致

AV1中的有效仿射模型需要同时满足式(11)和式(12)中的条件。
