阅读量:1
实验内容
(1)活动安排问题
设有n个活动的集合E={1, 2, …, n},其中每个活动都要求使用同一资源,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si <fi 。如果选择了活动i,则它在半开时间区间[si, fi)内占用资源。若区间[si, fi)与区间[sj, fj)不相交,则称活动i与活动j是相容的。 随机生成n个任务(n=8,16,32…),用贪心法求解,分析算法的时间复杂度,做出图像,横坐标为活动个数,纵坐标为执行时间。
(2)线段覆盖
问题描述:在一维空间中随机生成N(N=8,16,32…)条线段的起始坐标与终止坐标,要求求出这些线段一共覆盖了多大的长度(重叠区域只算一次)。分析算法的时间复杂度,画出算法的执行时间随N变化的曲线图。
实验结果
(1)活动安排问题

运行时间与n输入大小的曲线图
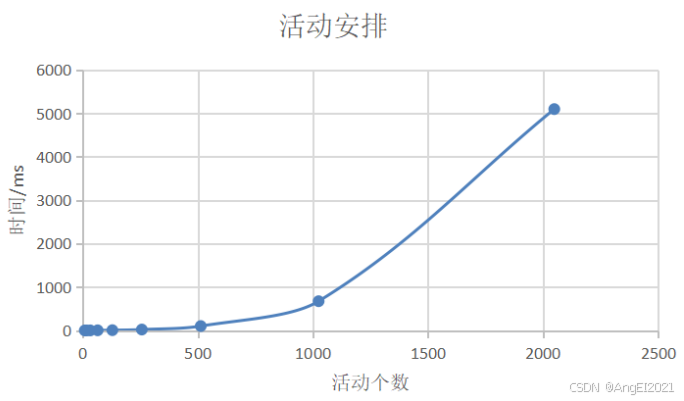
算法中将各个活动按照结束时间从小到大排序,时间复杂度为O(nlogn),依次考察每个活动,时间复杂度为O(n),算法的时间复杂度为O(nlogn)
(2)线段覆盖


运行时间由于输入个数的曲线图
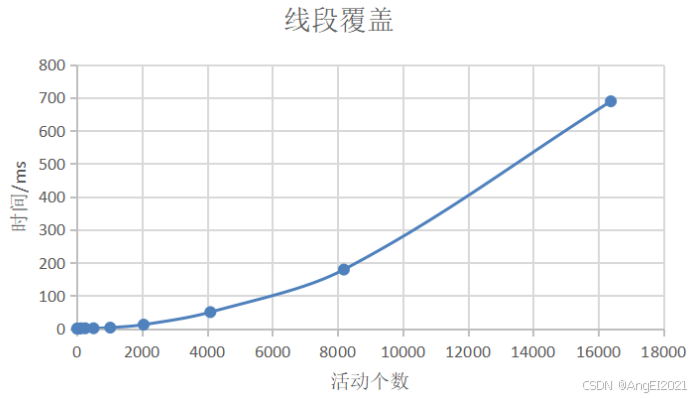
算法中对线段进行按起点排序的时间复杂度是O(nlogn),依次对剩余线段进行判断时的时间复杂度时O(n),整个算法的时间复杂度应为O(nlogn)
源代码
活动安排问题
#include<iostream> #include<time.h> using namespace std; void sort(int n, int s[], int f[])//按照结束时间非递减排序 { int a, b, i, j; for (i = 0; i < n; i++) for (j = i + 1; j < n; j++) if (f[i] > f[j]) { a = f[i]; f[i] = f[j]; f[j] = a; b = s[i]; s[i] = s[j]; s[j] = b; } } int Greedy(int n, int s[], int f[], bool B[]) { B[1] = true;//将第一个活动先安排 int j = 1, count = 1; //count为被安排的节目个数 for (int i = 2; i <= n; i++) { if (s[i] >= f[j])//活动i与集合B中最后结束的活动相容 { B[i] = 1;//安排活动i j = i; count++; } else B[i] = 0; } return count;//返回已安排的活动个数 } int main() { srand((unsigned int)time(NULL)); int a, b, n, i; bool B[2048]; int s[2048], f[2048]; clock_t start, end; cout << "输入n的大小:"; cin >> n; for (i = 0; i < n; i++) { a = rand() % 1000 + 1; b = rand() % 1000 + 1; if (a > b) { f[i] = a; s[i] = b; } else { s[i] = a; f[i] = b; } } start = clock(); for (i = 0; i < n; i++) sort(n, s, f); int g=Greedy(n, s, f, B); cout << "活动安排的个数是:" << g << endl; for (i = 1; i <= n; i++) cout << B[i] << " "; end = clock(); cout << endl; cout << "安排活动耗时:" << double(end - start)*1000 / CLOCKS_PER_SEC<<" ms"; return 0; }线段覆盖
#include<iostream> #include<time.h> using namespace std; struct line//线段结构体 { int start; int end; }; void sort(line l[], int n)//将线段按照大小排序 { int i, j; line temp, temp1; for (i = 0; i < n; i++) for (j = 0; j < n - i - 1; j++) { if (l[j].start > l[j + 1].start) {//起点小的在前面 temp = l[j]; l[j] = l[j + 1]; l[j + 1] = temp; } if (l[j].start == l[j + 1].start && l[j].end > l[j + 1].end) {//起点相同则终点小的在前面 temp1 = l[j]; l[j] = l[j + 1]; l[j + 1] = temp1; } } } int cover(line l[], int n, int length) { int i, len = length; if (n == 1)//只有一个线段直接返回长度 return len; for (i = 1; i < n; i++) { if (l[i].start >= l[i - 1].start && l[i].start <= l[i - 1].end && l[i].end >= l[i - 1].end) len += l[i].end - l[i - 1].end;//线段长度增加两终点之差 else if (l[i].start >= l[i - 1].end) len += l[i].end - l[i].start;//线段长度增加当前线段的长度 else if (l[i].start >= l[i - 1].start && l[i].end <= l[i - 1].end) l[i].end = l[i - 1].end;//线段长度不增加 } return len; } int main() { line l[16384]; int n, i, ln, length; clock_t cstart, cend; srand((unsigned)time(NULL)); cout << "输入线段的个数:"; cin >> n; cstart = clock(); for (i = 0; i < n; i++) { l[i].start = rand() % 100 + 1; l[i].end = rand() % 100 + 1; } sort(l, n);//对所有线段进行排序 ln = l[0].end - l[0].start; length = cover(l, n, ln);//求线段覆盖的长度 cend = clock(); cout <<"线段覆盖长度:"<< length << endl; cout << "耗时" << double(cend - cstart) * 1000 / CLOCKS_PER_SEC << " ms" << endl; return 0; }感谢大家的观看
