阅读量:8
目录
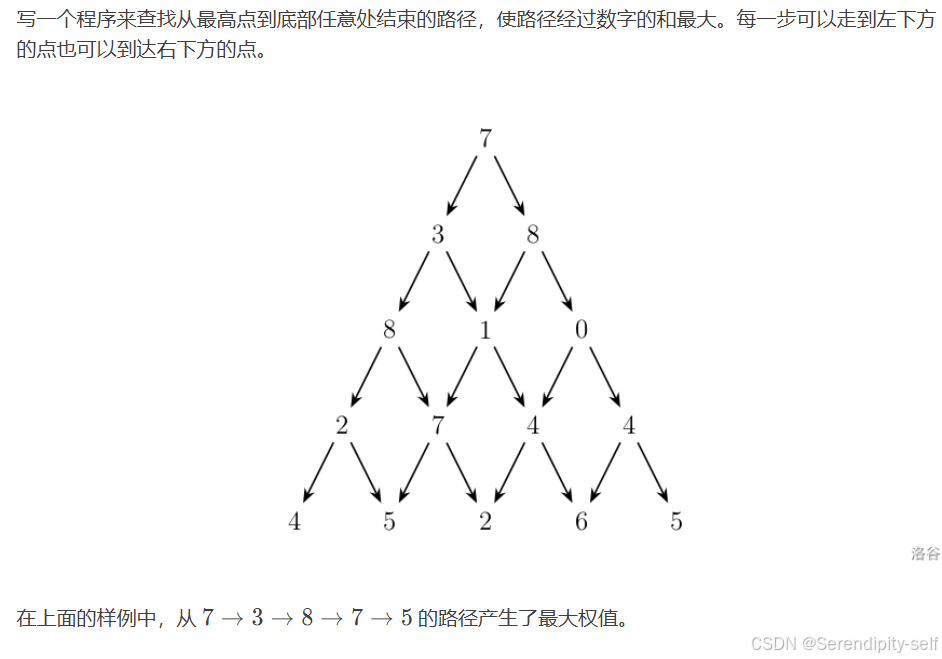
题目1： P1216 [USACO1.5] [IOI1994]数字三角形 Number Triangles
题目1： P1216 [USACO1.5] [IOI1994]数字三角形 Number Triangles
代码示例：
// c++ 代码示例 #include <algorithm> #include <iostream> using namespace std ; int n,a[1005][1005],f[1005][1005] ; int dfs(int x, int y) { if (x == n) return a[x][y] ; if (f[x][y] != -1) return f[x][y] ; return f[x][y] = max(dfs(x + 1, y), dfs(x + 1, y + 1)) + a[x][y] ; } int main() { int n ; cin >> n ; for (int i = 1 ; i <= n ; i++) { for (int j = 1 ; j <= i ; j++) { cin >> a[i][j] ; } } for (int i = 1 ; i <= n ; i++) { for (int j = 1 ; j <= i ; j++) { f[i][j] = -1 ; } } cout << dfs(1, 1) ; return 0 ; }// c++ 代码示例 #include <algorithm> #include <iostream> using namespace std ; long long n, a[1005][1005] ; int main() { cin >> n ; for (int i = 1 ; i <= n ; i++) { for (int j = 1 ; j <= i ; j++) { cin >> a[i][j] ; } } for (int i = n ; i >= 1 ; i--) { for (int j = 1 ; j <= i ; j++) { a[i][j] = a[i][j] + max(a[i + 1][j], a[i + 1][j + 1]); } } cout << a[1][1] ; return 0 ; }
// c++ 代码示例 #include <algorithm> #include <iostream> #include <cstdlib> #include <cstring> #include <cstdio> #include <string> using namespace std; #define rint register int inline void read(int &x) { x = 0; int w = 1; char ch = getchar(); while (!isdigit(ch) && ch != '-') { ch = getchar(); } if (ch == '-') { w = -1; ch = getchar(); } while (isdigit(ch)) { x = (x << 3) + (x << 1) + (ch ^ '0'); ch = getchar(); } x = x * w; } const int maxn = 1000 + 10; int n, a[maxn][maxn], ans; int main() { read(n); for (rint i = 1; i <= n; i++) { for (rint j = 1; j <= i; j++) { read(a[i][j]); if (i == 1 && j == 1) { // The top of the triangle continue; } if (j == 1) { // Left boundary a[i][j] += a[i - 1][j]; } else if (j == i) { // Right boundary a[i][j] += a[i - 1][j - 1]; } else { // Middle elements a[i][j] += max(a[i - 1][j - 1], a[i - 1][j]); } ans = max(ans, a[i][j]); } } cout << ans << endl; return 0; }
题目2： Common Subsequence
Common Subsequence - HDU 1159 - Virtual Judge (vjudge.net)
https://vjudge.net/problem/HDU-1159
代码示例
// c++ 代码示例 int a[MAXN], b[MAXN], f[MAXN][MAXN] ; int dp() { for (int i = 1 ; i <= n ; i++) { for (int j = 1 ; j <= m ; j++) { if (a[i - 1] == b[j - 1]) { f[i][j] = f[i - 1][j - 1] + 1 ; } else { f[i][j] = std::max(f[i - 1][j], f[i][j - 1]) ; } } } return f[n][m] ; }// c++ 代码示例 #include <cmath> #include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> #include <algorithm> using namespace std; char a[1001], b[1001]; int dp[1001][1001], len1, len2; void lcs(int i,int j) { for(i=1; i<=len1; i++) { for(j=1; j<=len2; j++) { if(a[i-1] == b[j-1]) dp[i][j] = dp[i-1][j-1] + 1; else if(dp[i-1][j] > dp[i][j-1]) dp[i][j] = dp[i-1][j]; else dp[i][j] = dp[i][j-1]; } } } int main() { while(~scanf(" %s",a)) { scanf(" %s", b); memset(dp, 0, sizeof(dp)); len1 = strlen(a); len2 = strlen(b); lcs(len1, len2); printf("%d\n", dp[len1][len2]); } return 0; }题目3 ：最长上升子序列
信息学奥赛一本通（C++版）在线评测系统 (ssoier.cn)http://ybt.ssoier.cn:8088/problem_show.php?pid=1281
最长不下降子序列
//c++代码示例 # include <iostream> # include <cstdio> using namespace std ; int n ; int a[1001] ; int f[1001] ; int mx = -1 ; int main() { scanf("%d", &n) ; for (int i = 1 ; i <= n ; i++) { scanf("%d", &a[i]) ; f[i] = 1 ; } for (int i = 2 ; i <= n ; i++) { for (int j = i - 1 ; j >= 1 ; j--) { if (a[i] >= a[j]) { f[i] = max(f[i], f[j] + 1) ; } } } for (int i = 1 ; i <= n ; i++) { mx = max(mx, f[i]) ; } printf("%d", mx) ; return 0 ; }//c++代码示例 # include <iostream> # include <cstdio> using namespace std ; int n ; int a[1001] ; int f[1001] ; int mx = -1 ; int main() { scanf("%d", &n) ; for (int i = 1 ; i <= n ; i++) { scanf("%d", &a[i]) ; f[i] = 1 ; } for (int i = n - 1 ; i >= 1 ; i--) { for (int j = i + 1 ; j <= n ; j++) { if (a[i] <= a[j]) { f[i] = max(f[i], f[j] + 1) ; } } } for (int i = 1 ; i <= n ; i++) { mx = max(mx, f[i]) ; } printf("%d", mx) ; return 0 ; }最长上升子序列oj答案
//c++代码示例 # include <iostream> # include <cstdio> using namespace std ; int n ; int a[1001] ; int f[1001] ; int mx = -1 ; int main() { scanf("%d", &n) ; for (int i = 1 ; i <= n ; i++) { scanf("%d", &a[i]) ; f[i] = 1 ; } for (int i = n - 1 ; i >= 1 ; i--) { for (int j = i + 1 ; j <= n ; j++) { if (a[i] < a[j]) { f[i] = max(f[i], f[j] + 1) ; } } } for (int i = 1 ; i <= n ; i++) { mx = max(mx, f[i]) ; } printf("%d", mx) ; return 0 ; }