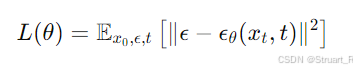目录
导言
笔者早些时候曾粗略看过扩散模型的流程,但对于底层算法(尤其是概率论方面),理解不够透彻,所以重新解释底层算法。
一、基础知识
1、数学期望
在扩散模型中经常使用数学期望来计算扩散模型的损失函数,其中期望符号的写法与概率论有所不同。

期望计算:对于变量x在概率密度函数为p(x)下的期望(亦说为变量x在p(x)分布下的期望)记作: 。由于一般来说概率密度函数p(x)已知,所以也缩写为
。由于一般来说概率密度函数p(x)已知,所以也缩写为 。而扩散模型中分布函数未知,所以记作前者。
。而扩散模型中分布函数未知,所以记作前者。
2、概率表示
 表示:0时刻下的概率分布。
表示:0时刻下的概率分布。
 表示:0到T时刻下,变量x的联合概率分布,此时不一定等于
表示:0到T时刻下,变量x的联合概率分布,此时不一定等于 ,因为不一定相互独立。
,因为不一定相互独立。
 表示:考虑0时刻情况
表示:考虑0时刻情况 成立下,1到T时刻下,变量x的联合概率分布。
成立下,1到T时刻下,变量x的联合概率分布。
由于扩散模型遵循马尔科夫链,所以一定有1时刻完全依赖于0时刻,2时刻完全依赖于1时刻,则可以理解为相互独立。
此时遵循贝叶斯公式: 。
。
对于T时刻与0时刻之间的关系:
3、KL散度
KL散度定义:

KL散度用来描述两个分布之间的距离,KL散度为0则两个分布相同,散度越大则越不相关。
KL散度非负性证明?
从凸函数定义延伸出Jetson不等式:
凸函数定义:
Jensen不等式(琴生不等式):当 是区间
是区间![[a,b]](/zb_users/upload/2024/csdn/eq.png) 的凸函数,则对于任意实数
的凸函数,则对于任意实数![x_1,x_2,...,x_n \in [a,b]](/zb_users/upload/2024/csdn/eq.png) ,对所有非负实数
,对所有非负实数  ,且
,且 ,下式成立:
,下式成立:

由KL散度定义:

其中:

由于 为凹函数所以提取负号,进行变换:
为凹函数所以提取负号,进行变换:


因此KL散度恒为非负。
二、扩散过程
扩散模型就是逐次往图片里加入高斯噪声直到完全变为噪声的过程,问题在于噪声如何加,与上一帧的加权关系。
噪声模型,本身是从一个正态分布中采样而来,分布遵循N(0,I)。
扩散前提:保证扩散后图像仍然是一个高斯噪声图像。
扩散迭代公式: ,保证扩散过程是一个均值
,保证扩散过程是一个均值 ,方差为
,方差为 的正态分布,
的正态分布, 是一个随时间变化的值,满足特定的差异时间表。
是一个随时间变化的值,满足特定的差异时间表。
均值为什么要乘以 ?
?
由于 时刻,保证
时刻,保证 仍然是一个正态分布,但显然现实场景T达不到无穷大,该想法只是一个理想条件。
仍然是一个正态分布,但显然现实场景T达不到无穷大,该想法只是一个理想条件。
扩散模型满足马尔科夫链:
对于扩散模型T时刻的通项公式:
通项公式计算如下:
令
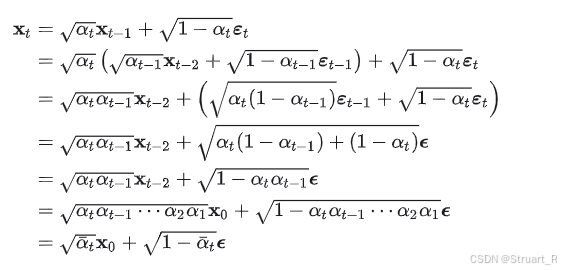
三、理想的去噪过程
去噪过程的思想就是从随机噪声中还原一个图像。
目的:求出 迭代公式。
迭代公式。
但由于我们无法通过原有的 来反向推导该目标,所以我们尝试用神经网络(一般用u-net)拟合一个
来反向推导该目标,所以我们尝试用神经网络(一般用u-net)拟合一个 ,与目标近似。
,与目标近似。
迭代公式推导主体思想:化反向过程为前向过程!
首先对于 公式进行转化:
公式进行转化:

7.1步用贝叶斯公式替换,7.2步乘法公式展开,7.3步进行整理,7.4步带入正态分布函数公式,由于差了一个 ,所以不完全等价,保证正比于。7.5步转换为关于
,所以不完全等价,保证正比于。7.5步转换为关于 的二次项函数,此时可以抽出方差和均值,这两者均
的二次项函数,此时可以抽出方差和均值,这两者均 有关。
有关。
迭代公式:
最后证明为一个变量为t-1时刻的前向过程。
四、真实的去噪过程
真实的去噪过程是预测噪声分布,一般计算变分自编码器的最大化证据下界,训练方法就是最小化负对数似然。
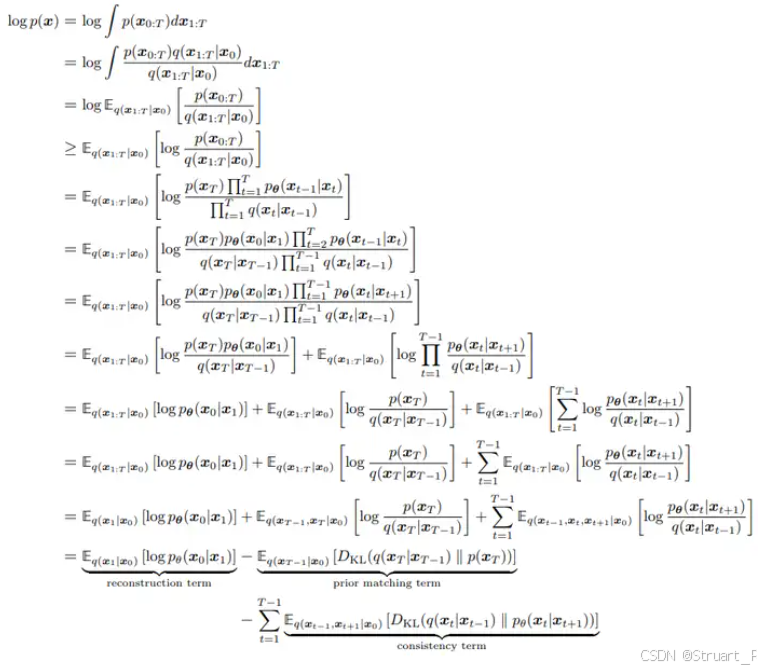
上面结果中第一项约束最终第T步得到的加噪结果  接近于完全的高斯噪声,最后一项约束模型生成的结果与真值接近,而中间的 t-1 项约束逆向过程的马尔科夫链中,神经网络估计出的每一个条件分布接近于对应的真实的数据分布。
接近于完全的高斯噪声,最后一项约束模型生成的结果与真值接近,而中间的 t-1 项约束逆向过程的马尔科夫链中,神经网络估计出的每一个条件分布接近于对应的真实的数据分布。
中间的第t项的KL散度可以进行化简,最后将收敛于真实噪声,如下。
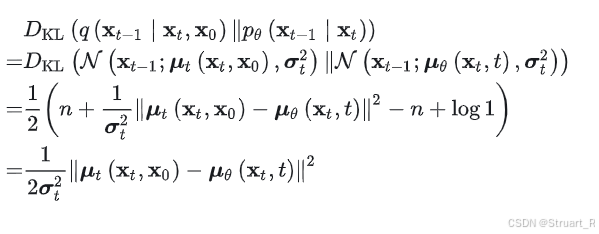
代入推导出来的均值,此时正比于一个真实噪声与预测噪声的均方误差,这个结构最后作为损失函数用于最小化。
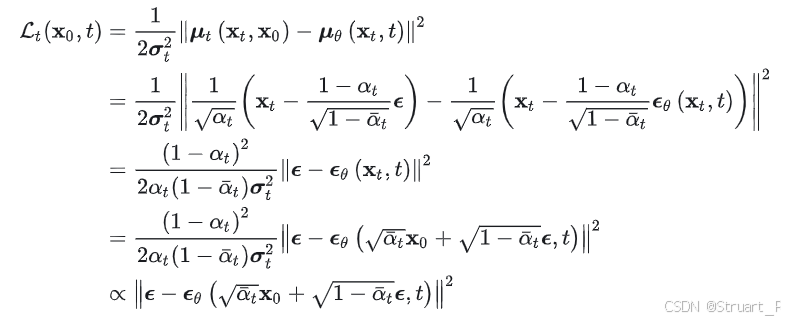
五、噪声生成
噪声生成模型一般用U-net或U-net结合transformer,输入带有噪声的图像和时间步t,输出是预测出的 ,损失函数用真实噪声与预测噪声的均方误差。
,损失函数用真实噪声与预测噪声的均方误差。