目录
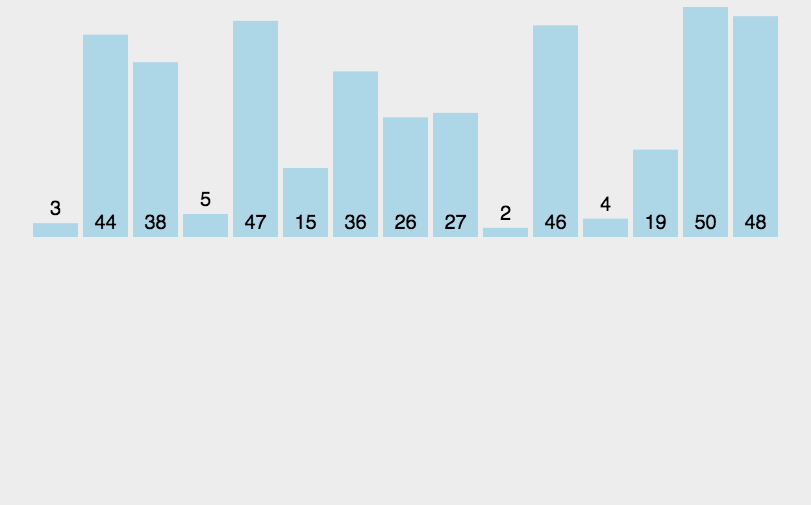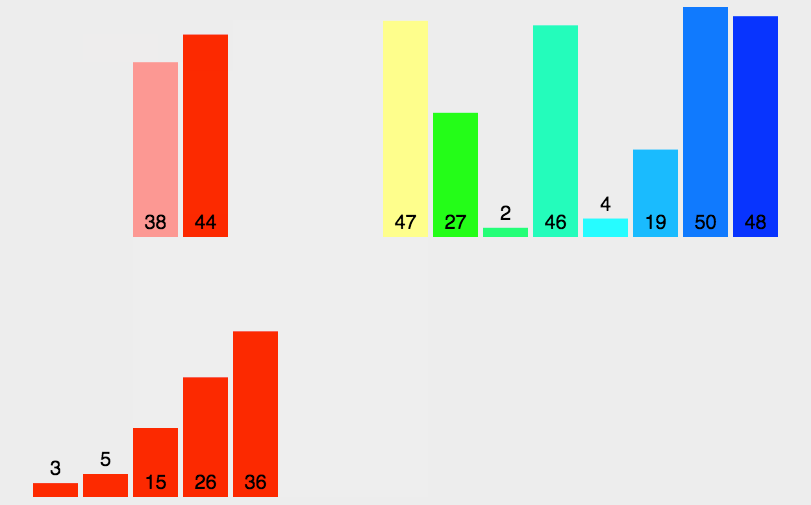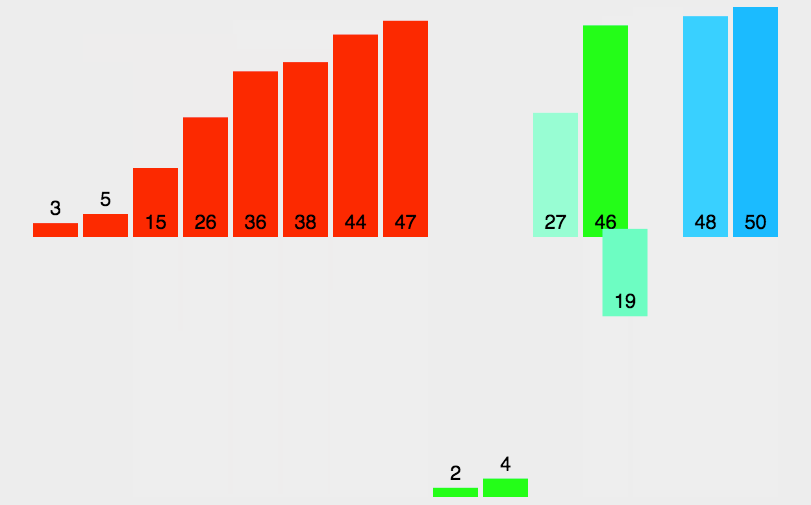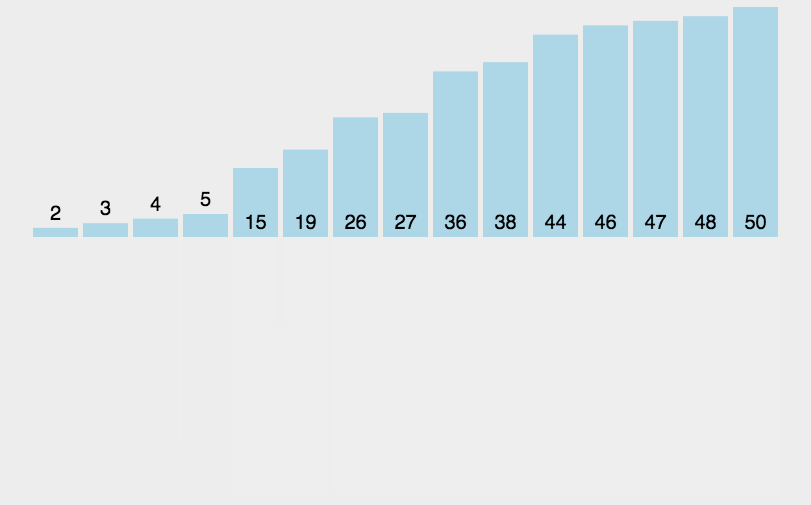
快速排序
一. 快速排序递归的实现方法
1. 左右指针法
步骤思路
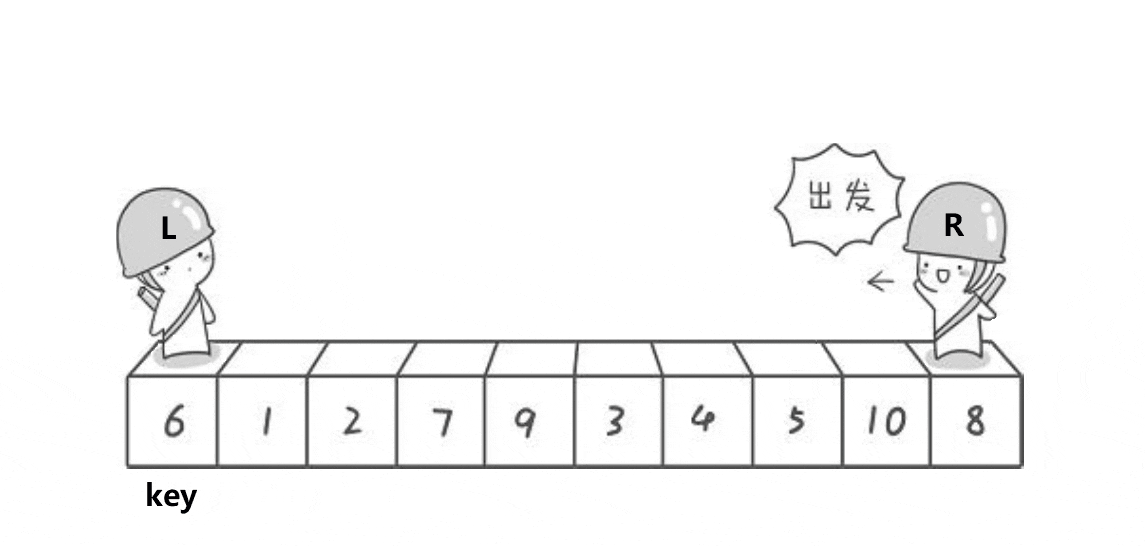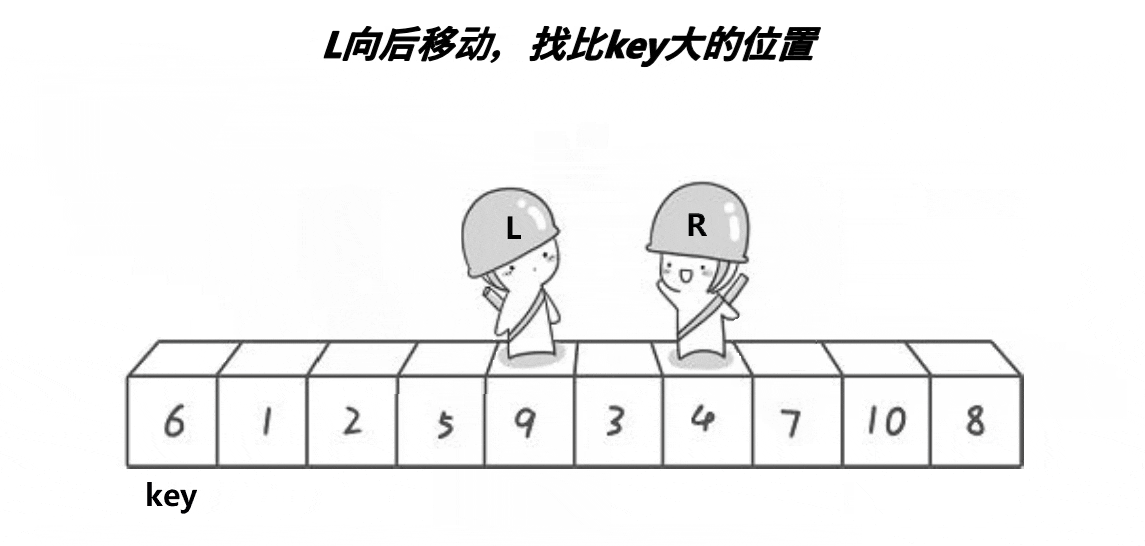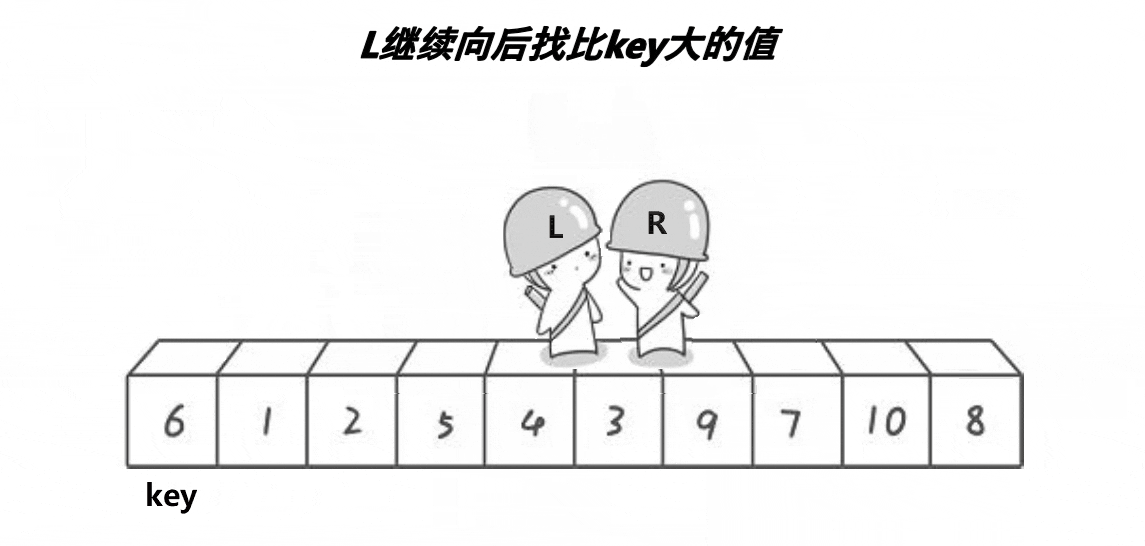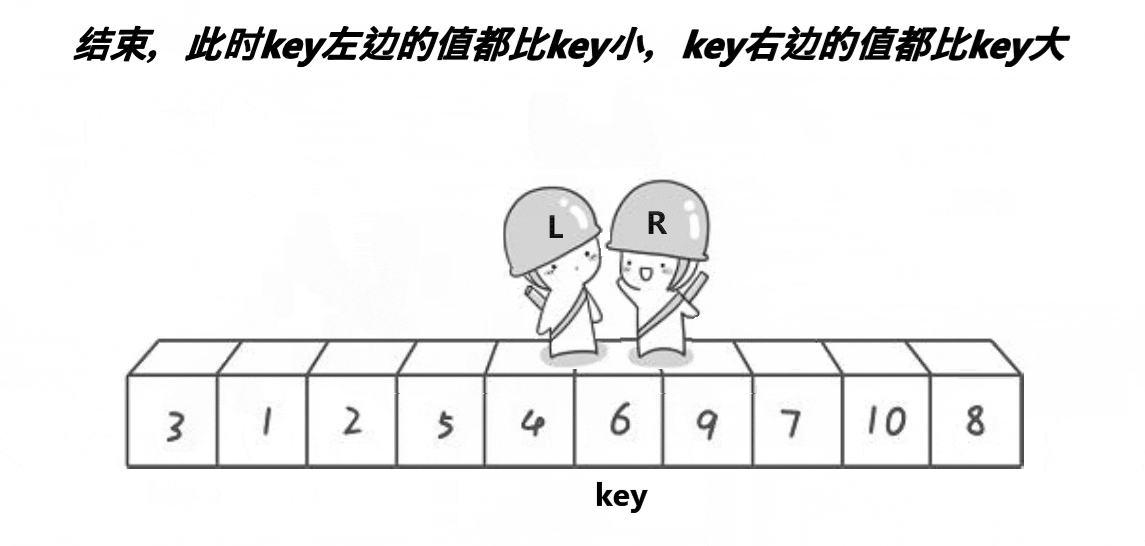
(假设排升序)将数组a最左边的下标用begin记录下来,最右边用end记录下来,定义一个key为begin或end
(假设key定义为begin)end先向左查找找到<a[key]的数停下,begin再向右查找找到>a[key]的值停下,此时将begin指向的值与end指向的值交换,以此类推直到end的值<=begin,将此时的a[key]与begin与end相遇坐标的值交换,我们发现此时的a[key],左边的值都比其小,右边的值都比其大,那就说明key所指向的值在数组中已经排好位置了
如以下代码,即完成了单趟
int key = left; int begin = left, end = right; while (begin < end) { while (a[end] >= a[key] && begin < end) { end--; } while (a[begin] <= a[key] && begin < end) { begin++; } Swap(&a[begin], &a[end]); } Swap(&a[key], &a[begin]);我们在end和begin寻找比a[key]大或小的值的时候不要忘记也要判断循环成立的条件
既然key已经在数组排好位置,我们接下来递归就不需要加上key了,只需要递归key的左右区间即可,直到递归的区间左边与右边相等即只有一个数
完整代码如下
void QuickSort1(int* a, int left,int right) { if (left >= right) return; int mid = GetMid(a, left, right); Swap(&a[mid], &a[left]); int key = left; int begin = left, end = right; while (begin < end) { while (a[end] >= a[key] && begin < end) { end--; } while (a[begin] <= a[key] && begin < end) { begin++; } Swap(&a[begin], &a[end]); } Swap(&a[key], &a[begin]); QuickSort1(a, left, begin - 1); QuickSort1(a, begin + 1, right); }为什么要让end先走?
左边做key右边先走,可以保证相遇位置比key小
相遇场景分析
begin遇end:end先走,停下来,end停下条件是遇到比key小的值,end停下来的位置一定比key小,begin没有找到大的遇到end停下了
end遇begin:end先走,找小,没有找到比key更小的,直接跟begin相遇了。begin停留的位置是上一轮交换的位置(即,上一轮交换,把比key小的值,换到begin的位置了)
同样道理让右边做key,左边先走,可以保证相遇位置比key要大
2. 挖坑法
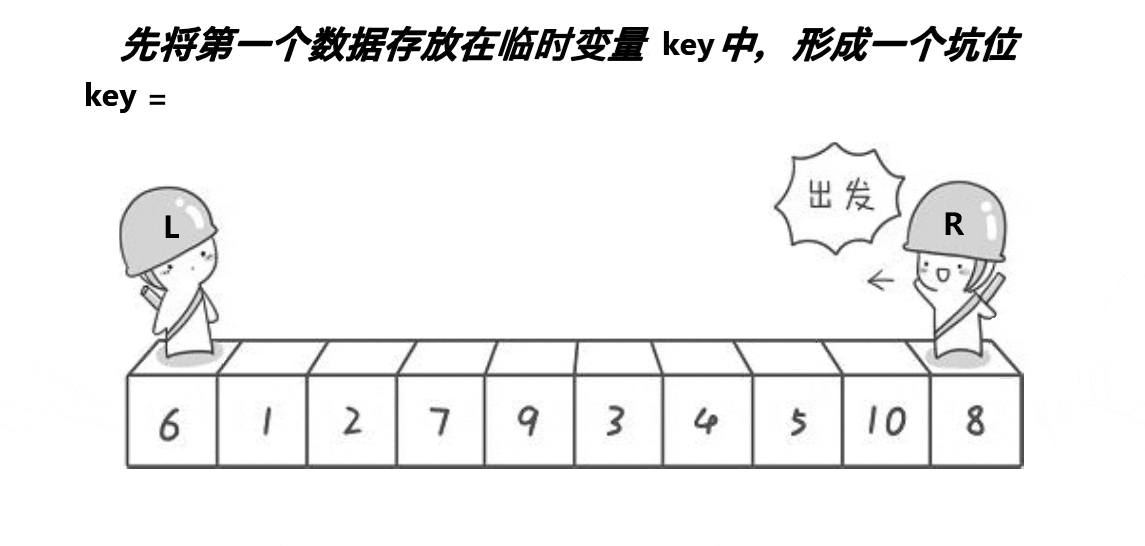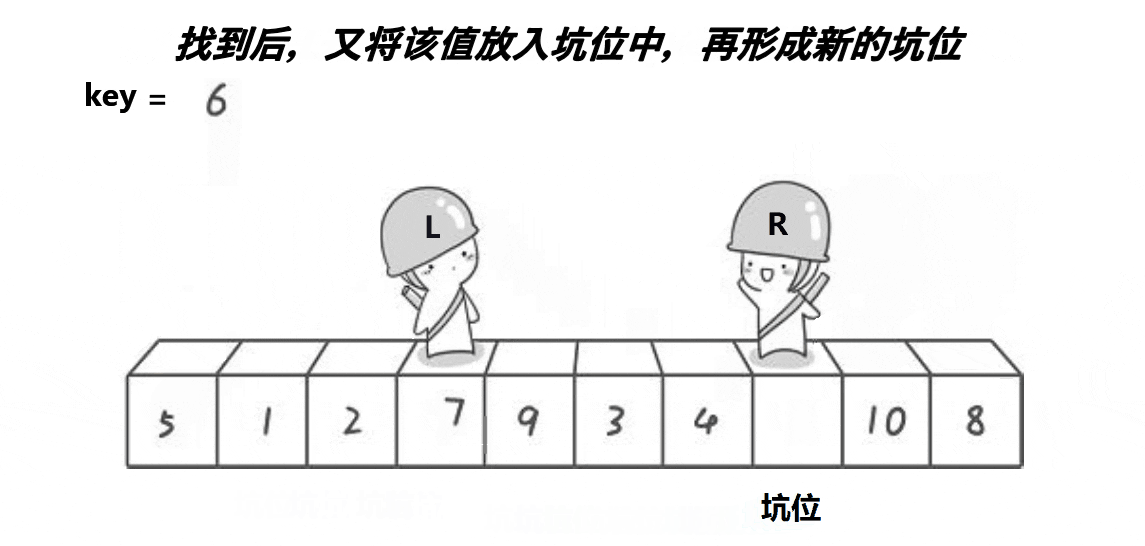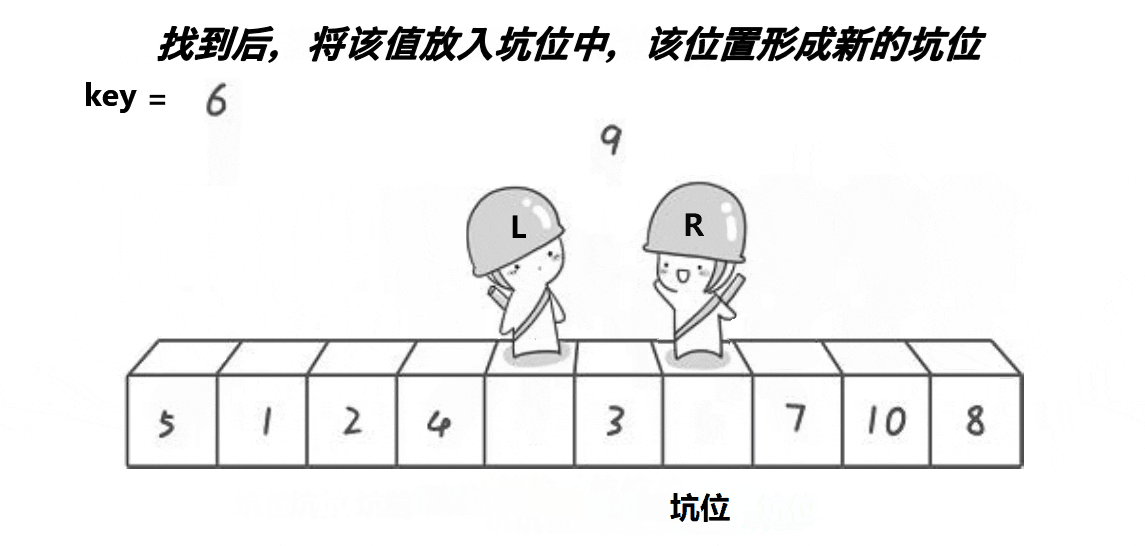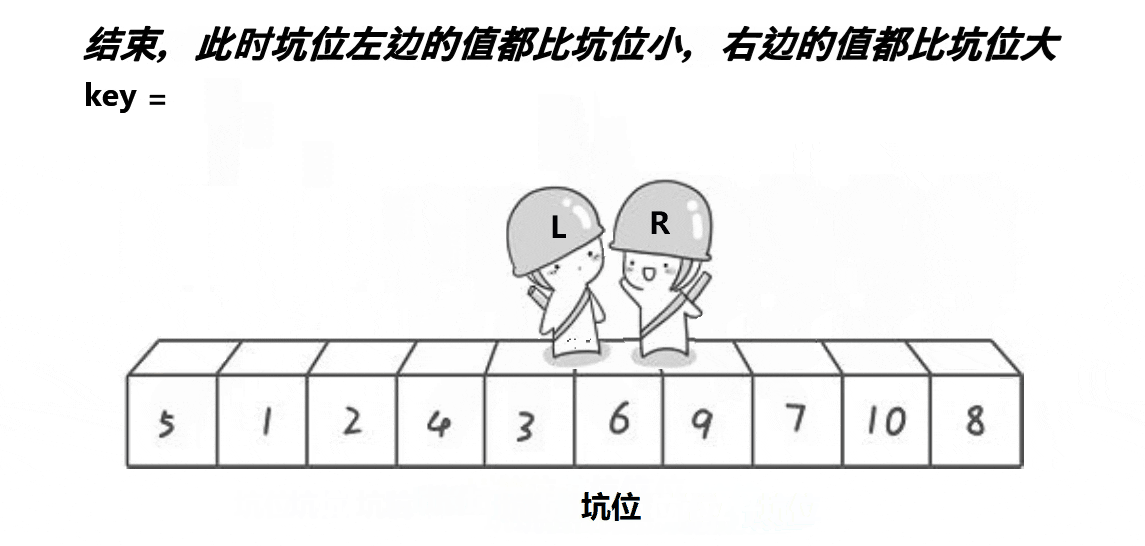
步骤思路
(假设排升序,给数组a)将最左边的值定义key存储起来,最左边的下标用bigen记录,最右边的下标用end记录,定义pivot记录为最左边的下标,即将最左边视为坑位
然后end向左寻找比key小的值放到pivot所指向的位置即坑位中,并将这个地方(end所找到的)视作新的坑(更新pivot的值)。
begin向右寻找比key大的值,放到坑位中,并将这个地方视作新的坑(更新pivot的值)
重复以上步骤直到end<=begin
然后将key填进pivot中,再通过递归,即可完成排序
由于与左右指针法类似就不写单趟,直接上完整代码
void QuickSort2(int* a, int left, int right) { if (left >= right) return; int key = a[left]; int begin = left, end = right; int pivot = left; while (begin < end) { while (a[end] >= key && begin < end) { end--; } a[pivot]=a[end]; pivot = end; while (a[begin] <= key && begin < end) { begin++; } a[pivot] = a[begin]; pivot = begin; } a[pivot] = key; QuickSort2(a, left, pivot - 1); QuickSort2(a, pivot + 1, right); }3. 前后指针法
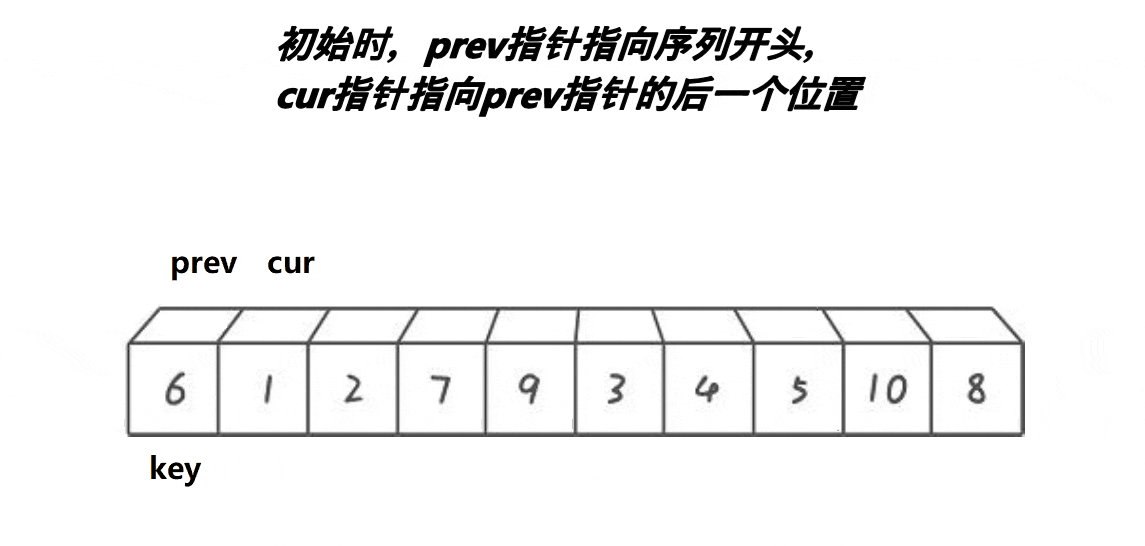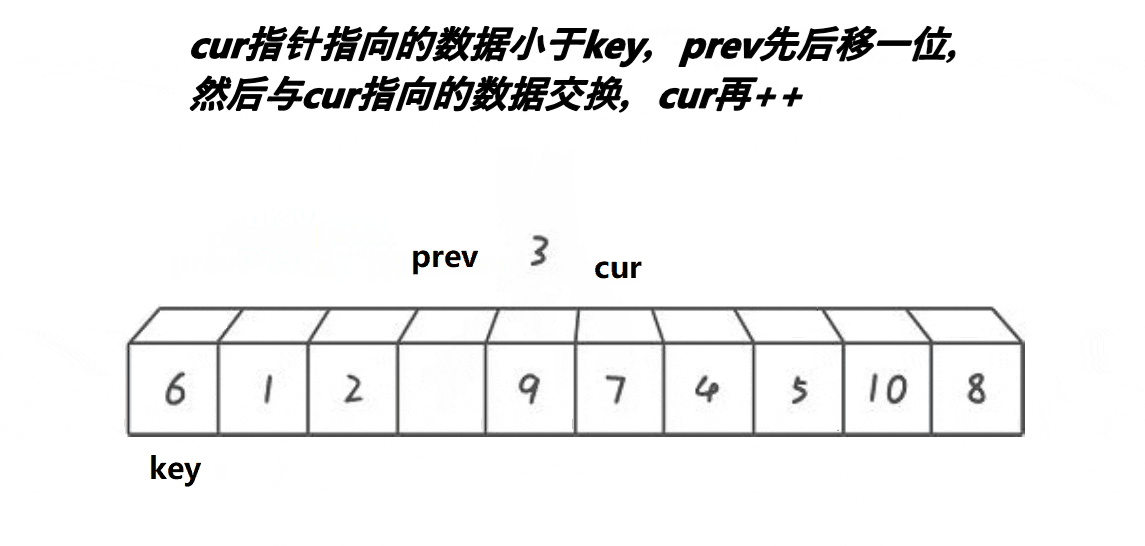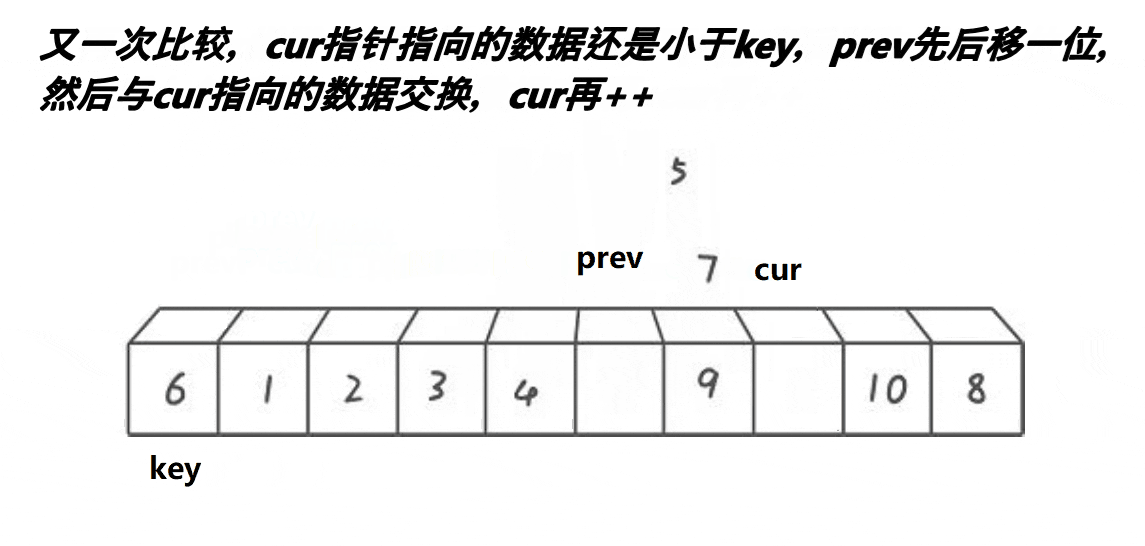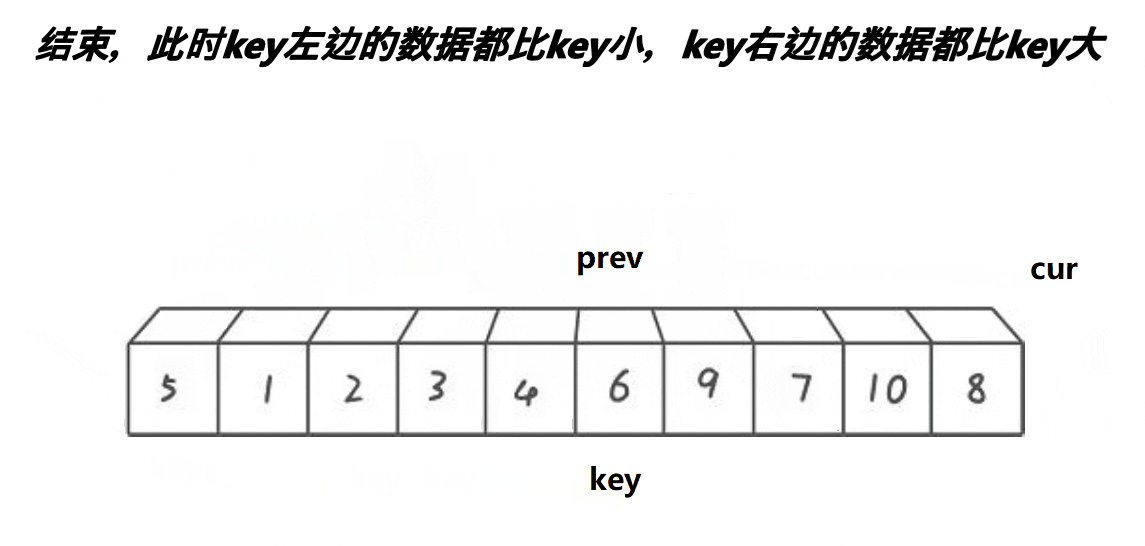
步骤思路
(假设排升序)定义key为数组最左边的下标,并定义,prev=key与after=key+1
after在找到比key指向的值小的值时,prev++,并将after指向的值与现在的prev(即prev++后的值)交换
以此往复,直到after>数组的值
然后将prev所指向的值与key所指向的值交换
代码如下
我们要注意,当prev++后的值==after就会发生与自身交换
完成一次后,效果依然是a[key]左区间的值比其小,右区间的值比其大
int key = left; int prev = left, after = left + 1; while (after<=right) { while (a[after] < a[key]&&++prev!=after) { Swap(&a[prev], &a[after]); } after++; } Swap(&a[prev], &a[key]);递归是和上面两种方法同样的道理
完整代码如下
void QuickSort3(int* a,int left,int right) { if (left >= right) return; int key = left; int prev = left, after = left + 1; while (after<=right) { while (a[after] < a[key]&&++prev!=after) { Swap(&a[prev], &a[after]); } after++; } Swap(&a[prev], &a[key]); QuickSort3(a, left, prev - 1); QuickSort3(a, prev + 1, right); }二. 快速排序的时间和空间复杂度
1. 时间复杂度
①最好情况
每次的划分都使得划分后的子序列长度大致相等,一般在数据已经部分有序或者随机分布的情况下发生。此时时间复杂度为O(Nlog₂N)
②最坏情况
在待排序序列有序的情况下,每一次划分的两个区间都有一个为0,此时快速排序的时间复杂度退化为O(N²)
③平均情况
实际应用中快速排序的平均情况大概会接近于最好情况,因为待排序序列通常不是有序的,我们还可以通过三数取中来优化,减少最坏情况的可能性,所以快速排序的时间复杂度为O(Nlog₂N)
2. 空间复杂度
由于需要递归调用,相当于求递归树的深度,
①最坏情况
当数组接近有序时,递归深度很深,空间复杂度为O(N)
②最好情况
当数组无序时,递归树基本相当与完全二叉树,空间复杂度为O(log₂N)
③平均情况
实际应用中,平均情况大概会接近最好情况,同样可以用三数取中优化
所以快速排序空间复杂的为O(log₂N)
三. 快速排序的优化方法
1. 三数取中优化
为了让每次左右区间长度接近,我们可以使用三数取中,即最左边最右边与中间的值取不大也不小的一个值并返回
int GetMid(int* a, int left, int right) { int mid = (left + right) / 2; if (a[left] < a[mid]) { if (a[mid] < a[right]) return mid; else if (a[left] < a[right])//上面if条件不成立可得a[right]<a[mid] return right; else//又可得 a[left] > a[right] return left; } else//a[left]>=a[mid] { if (a[mid] > a[right]) return mid; else if (a[left]< a[right])//上面if条件不成立可得a[right]>a[mid] return left; else//又可得 a[left] < a[right] return right; } } 将返回值接收并将其指向位置与最左边的值交换,代码如下
if (left >= right) return; int mid = GetMid(a, left, right); Swap(&a[mid], &a[left]); int key = left;2. 小区间优化
当快速排序要排的数据很长时,越递归到后面区间越小递归的层数越多,我们可以考虑,当要递归区间小于10的时候用别的排序来代替,这样就可以省去80%到90%的递归
代码如下
void QuickSort1(int* a, int left,int right) { if ( (right-left+1)<10)//小区间优化 { InsertSort(a+left, right - left + 1); //a+left 有可能是后半段区间 //减少递归层数 } else { if (left >= right) return; int mid = GetMid(a, left, right); Swap(&a[mid], &a[left]); int key = left; int begin = left, end = right; while (begin < end) { while (a[end] >= a[key] && begin < end) { end--; } while (a[begin] <= a[key] && begin < end) { begin++; } Swap(&a[begin], &a[end]); } Swap(&a[key], &a[begin]); QuickSort1(a, left, begin - 1); QuickSort1(a, begin + 1, right); } }四. 使用栈来实现非递归快排
栈的实现可以看一下我以前的博客
步骤思路
初始化栈后,将数组的最右边与最左边分别放入栈(即将一个区间放入栈中)
进入循环(当栈为空时循环结束),用begin和begin1接收栈顶端的值,再删除栈的值,再用end和end1接收栈顶端的值,再删除栈的值,使用左右指针法(挖坑法,前后指针法皆可)(用begin与end来寻找值,begin1与end1不变)进行一趟排序,
如果right1>=begin+1 就往栈里存 right1(当前排序区间的最右边) 和 begin+1 反之不存
如果left1<=begin-1 就往栈里存 begin-1 和 left1(当前排序区间的最左边) 反之不存
最后不要忘记销毁栈
代码如下
void StackQuickSort(int* a, int left, int right) { ST s; StackInit(&s); StackPush(&s, right); StackPush(&s, left); while (!StackEmpty(&s)) { int begin = StackTop(&s); int left1 = begin; StackPop(&s); int end = StackTop(&s); int right1= end; StackPop(&s); int key = begin; //int mid = GetMid(a, begin, end); //Swap(&a[mid], &a[begin]); while (begin < end) { while (a[end] >= a[key] && begin < end) { end--; } while (a[begin] <= a[key] && begin < end) { begin++; } Swap(&a[begin], &a[end]); } Swap(&a[key], &a[begin]); if(right1>=begin+1) { StackPush(&s,right1); StackPush(&s, begin + 1); } if(left1<=begin-1) { StackPush(&s, begin - 1); StackPush(&s, left1); } } StackDestroy(&s); }归并排序
一. 归并排序的递归实现
步骤思路
malloc一个临时数组进入子函数(创建子函数递归会更方便),进行递归,子函数利用分治思想一直递归直到left>=right 开始执行下面操作
k赋初值为当前区间最左边,begin1 , end1来记录左数组最左边和最右边,定义begin2 ,end2 来记录右数组的最左边和最右边,将两个数组从头比较,较小的赋值给临时数组,直到有一方赋完值,再将没赋完值的数组给临时数组赋值。最后给要排序数组left到right赋值为临时数组left到right
代码如下
//递归 void _MergeSort(int* a,int* tmp, int left, int right) { if(left>=right) { return; } int mid = (left + right) / 2; //如果[left,mid][mid+1,right]有序就可以归并了 _MergeSort(a,tmp, left, mid); _MergeSort(a,tmp, mid + 1, right); int begin1 = left; int end1 = mid; int begin2 = mid + 1; int end2 = right; int k=left; while (begin1 <= end1&&begin2<=end2) { if(a[begin1]<a[begin2]) { tmp[k++] = a[begin1++]; } else { tmp[k++] = a[begin2++]; } } while (begin1 <= end1) { tmp[k++] = a[begin1++]; } while (begin2 <= end2) { tmp[k++] = a[begin2++]; } for (int i = left; i <= right; i++) { a[i] = tmp[i]; } } void MergeSort(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc fail"); return; } //_MergeSort(a, tmp, 0, n - 1); _MergeSort2(a,tmp, n); free(tmp); tmp = NULL; }二. 时间复杂度与空间复杂度
1. 时间复杂度
归并排序的时间复杂度是稳定的,不受输入数组的初始顺序影响
将数组分成两个子数组的时间复杂度为O(1),递归对子数组进行排序,假设每个子数组长度为n
则两个子数组排序的总时间复杂度为O(NlogN),将两个有序数组合并为一个有序数组时间复杂度为O(N),所以归并排序时间复杂度为O(NlogN)
2. 空间复杂度
调用栈所需要的额外空间为O(logN),因为我们需要一个额外数组来存储数据所以又额外消耗O(N)的空间,我们将较小的O(logN)忽略可以得到归并排序的空间复杂度为O(N)
三. 非递归实现归并排序
步骤思路
开辟动态空间后定义一个数gap=1来控制区间(gap相当于每组数据个数),(每一次gap*2,使每次区间扩大)gap<数组长度
设计一个for循环i+=gap*=2
每次分两组[i][i+gap-1]和[i+gap][i+2*gap-1] (i每次+=正好跳过这些数据)
将两个区间的值比较放入新开辟的数组,再拷贝到原数组
代码如下
//非递归 void _MergeSort2(int* a,int* tmp,int n) { int gap = 1; while(gap<n) { for (int i = 0; i < n; i += 2 * gap) { int begin1 = i; int end1 = i + gap - 1;; int begin2 = i + gap; int end2 = i + 2 * gap - 1; int k = i; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[k++] = a[begin1++]; } else { tmp[k++] = a[begin2++]; } } while (begin1 <= end1) { tmp[k++] = a[begin1++]; } while (begin2 <= end2) { tmp[k++] = a[begin2++]; } //memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1)); for (int j = i; j < k; j++) { a[j] = tmp[j]; } } gap *= 2; } } 但是我们发现,这样如果会发生越界的现象
一共三种可能
1. [begin1,end1][begin2,end2] end2越界
2. [begin1,end1][begin2,end2] begin2,end2越界
3. [begin1,end1][begin2,end2] end1,begin2,end2越界
第2,3种我们可以直接不递归了,因为后面区间的不存在前面区间的在上一次已经递归好了,
第一种呢我们需要把区间(即end)给修正一下
修正代码如下
//非递归 void _MergeSort2(int* a,int* tmp,int n) { int gap = 1; while(gap<n) { for (int i = 0; i < n; i += 2 * gap) { int begin1 = i; int end1 = i + gap - 1;; int begin2 = i + gap; int end2 = i + 2 * gap - 1; int k = i; if (begin2 >= n)//第二种情况,第二组不存在,不需要归并 break; if (end2 >= n)//第一种情况,需要修正一下 end2 = n - 1; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[k++] = a[begin1++]; } else { tmp[k++] = a[begin2++]; } } while (begin1 <= end1) { tmp[k++] = a[begin1++]; } while (begin2 <= end2) { tmp[k++] = a[begin2++]; } //memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1)); for (int j = i; j < k; j++) { a[j] = tmp[j]; } } gap *= 2; } } 排序算法的稳定性
假定在待排序的记录序列中,存在多个具有相同关键字的记录,若经过排序,这些记录的相对次序保持不变
即原序列中 r[i]=r[j],且r[i]在r[j]之前而在排序后的序列中r[i]仍在r[j]前,则称这种排序算法是稳定的,否则是不稳定的
| 冒泡选择 | 稳定 | |
| 选择排序 | 不稳定*** | 只会考虑自身,假如找到最小值1下标为3,将其与下标为0(假设此处为6)处交换若下标为1处也是6,就改变了 |
| 直接插入排序 | 稳定 | |
| 希尔排序 | 不稳定(分组) | 预排序时相同的值可能分到不同的组 |
| 堆排序 | 不稳定 | 建堆时可能就乱了 |
| 归并排序 | 稳定 | 当两个数相等,让第一个下来就是稳定的(可以控制) |
| 快速排序 | 不稳定 | end先找到 j 和begin交换了,在找到 i 和bigin交换,显然改变了 |
这篇文章就到这里了,感谢大家阅读
(๑′ᴗ‵๑)I Lᵒᵛᵉᵧₒᵤ❤