一、RRT路径规划算法原理
Rapidly-Exploring Random Trees (RRT) 路径规划算法是一种常用于机器人运动规划的算法,旨在通过随机采样和快速探索环境来生成可行路径。该算法由 Steven M. LaValle 在 1998 年提出,至今仍被广泛应用于各种机器人领域。
RRT 算法的核心思想是通过随机采样,在自由空间中快速构建一个树形结构,以探索可能的路径。在每次迭代中,算法随机生成一个节点,并试图将该节点连接到最接近的树节点,形成一条边。通过反复迭代这一过程,不断扩展树的范围,直至达到目标状态或达到最大迭代次数为止。
1.RRT算法流程
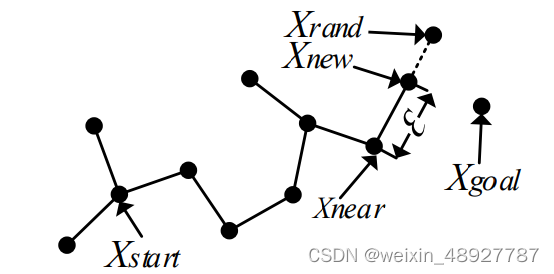
在初始阶段,将起点Xstart添加到随机树的根节点。然后,在地图空间中随机采样一个坐标点作为随机点Xrand,并找到距离随机点Xrand最近的树节点Xnear。接下来,沿着从Xnear到Xrand的方向扩展一个给定的步长 ,得到新节点Xnew。
,得到新节点Xnew。
新节点Xnew的生成分为两种情况:(1)如果Xnear到Xrand的距离大于步长δ,则在Xnear到Xrand的方向上扩展一个步长δ的位置作为Xnew;(2)如果Xnear到Xrand的距离小于等于步长δ,则直接将Xrand作为Xnew的位置。
然后,检测新节点Xnew是否通过了碰撞检测:如果通过了碰撞检测,则将其添加到随机树的根节点中;如果未通过碰撞检测,则重新迭代以寻找新的节点。
接着,判断新节点Xnew是否在目标点Xgoal的阈值范围内,若是,则返回根节点,路径规划完成。
2.RRT算法路径规划过程图
二、RRT算法伪代码

获取随机节点的代码为:
def generate_random_node(self): delta = self.utils.delta #delta为机器人半径大小,从而考虑路径宽度,避免与障碍物碰撞 return Node((np.random.uniform(self.x_range[0] + delta, self.x_range[1] - delta), np.random.uniform(self.y_range[0] + delta, self.y_range[1] - delta))) #x_range和y_range为地图长宽大小 获取临近点的代码为:
@staticmethod def nearest_neighbor(node_list, n): # node_list为随机树中的全部节点信息,n为随机点 return node_list[int(np.argmin([math.hypot(nd.x - n.x, nd.y - n.y) for nd in node_list]))]获取新节点的代码为:
def new_state(self, node_start, node_end): dist, theta = self.get_distance_and_angle(node_start, node_end) #node_start为临近点, node_end为随机点。 dist, theta分别为临近点向随机点的距离和角度 dist = min(self.step_len, dist) #self.step_len为扩展步长,找出扩展步长和两点距离的最小值 node_new = Node((node_start.x + dist * math.cos(theta), node_start.y + dist * math.sin(theta))) #获得新节点 node_new.parent = node_start #将临近点作为新节点的父节点,用以通过父节点,反向找到路径 return node_new @staticmethod def get_distance_and_angle(node_start, node_end): dx = node_end.x - node_start.x dy = node_end.y - node_start.y return math.hypot(dx, dy), math.atan2(dy, dx)新节点在目标点范围内,获得路径的代码为:
def extract_path(self, node_end): #node_end为在目标点范围的新节点 path = [(self.s_goal.x, self.s_goal.y)] #先将目标点加入path列表中 node_now = node_end #将该新节点作为当前节点 while node_now.parent is not None: #判断当前节点的父节点是否存在,如果存在就执行以下内容 node_now = node_now.parent #将当前节点的父节点作为当前节点,目的是重复找父节点,来寻找路径点 path.append((node_now.x, node_now.y)) #将当前节点加入path列表中 return path #重复以上内容,直到当前节点为起点时,没有父节点,结束循环,得到最终路径点三、RRT算法仿真结果
(1)简单环境
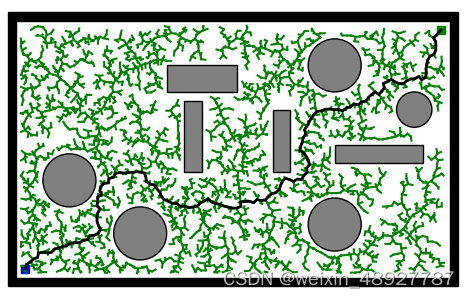
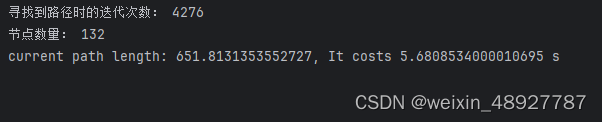
(2)狭窄环境
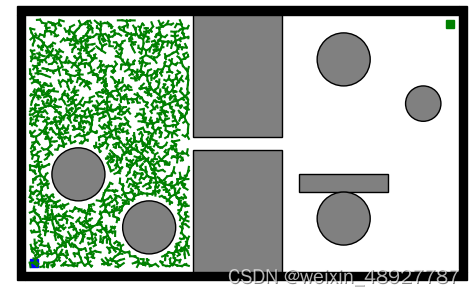
在狭窄环境下,这种算法如果没有足够的迭代次数,就很难找到路径。如上图所示。
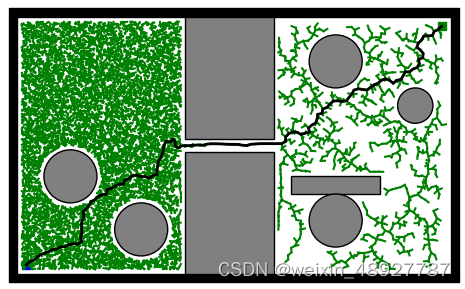
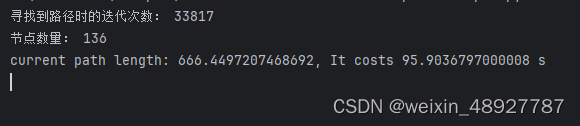
而给了它足够的迭代次数后,虽然能找到路径,但是算法所用的迭代次数和运行时间相比于在简单环境下,无疑也是大大增加。 如上图所示。
四、RRT算法优缺点
从以上两种地图环境可以看出:
RRT 算法具有几个显著的优点。首先,它适用于高维和复杂环境,能够快速生成可行路径。其次,由于采用了随机采样的策略,因此能够有效应对未知环境和动态障碍物。此外,RRT 算法还能够在运行过程中动态调整树的结构,以适应不同的环境条件。
然而,RRT 算法也存在一些局限性。由于其随机性质,算法在生成新节点时没有目标引导性,导致算法随机性较强。另外,算法在搜索过程中对空间的搜索范围较大,这样无疑是在浪费运行的计算量和运行时间。还要考虑的是,随机点引导的新节点所生成的路径可能不够优化,导致路径长度较长或存在不必要的曲折。此外,在某些情况下,算法可能会陷入局部最优解,无法找到全局路径,致使算法规划路径成功率较低。
