这篇文章充分借鉴了这篇文章,基本就是拿这个当模板做的,非常感谢这个文章的作者
链接:https://blog.csdn.net/Lvoving/article/details/128762328
————————————————
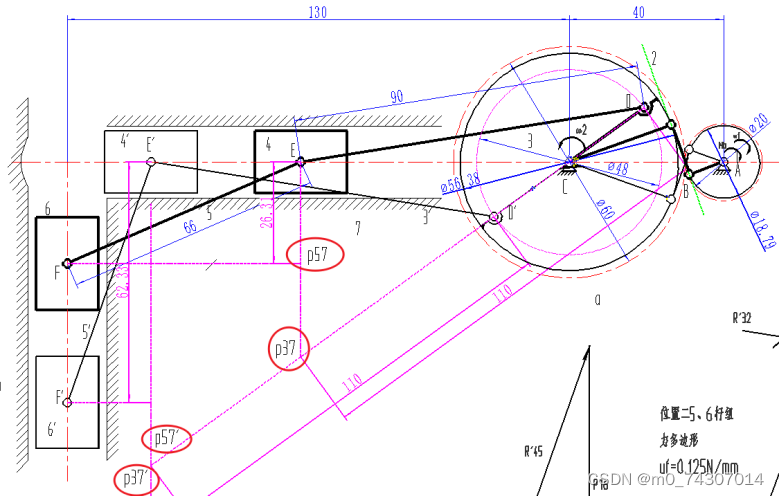
右侧齿轮为齿轮一,匀速转动,顺时针360rpm,左侧齿轮为齿轮二
!!!本文中多项式的length用的 l 代替的
这里面做了一些速度瞬心,是图解法用到的,这里解析法请忽略
当 theta2 > 144*pi/180 && theta2 < 216*pi/180 的时候,滑块4受到向右的生产阻力227N。
表示角度的theta均为与横轴向右的夹角,如下图(有一个命名为theta的数组,包含了角位移和线位移)length4和length6均为E点和F点的位移,在如下坐标系中为负位移,为了保持一致,设L为-130。

根据两个封闭图形列出矢量在x轴、y轴的投影关系
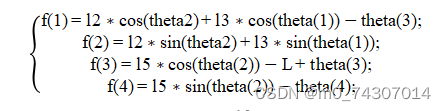
其中L代表-130
求一阶导数
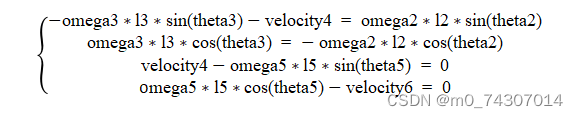
将上述一阶导数的方程组写成矩阵形式
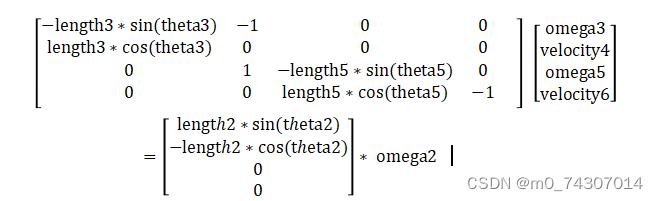
在matlab中:
设A阵
A=[-length3*sin(theta(1)),-1,0,0;
length3*cos(theta(1)),0,0,0;
0,1,-length5*sin(theta(2)),0;
0,0,length5*cos(theta(2)),-1];
设B阵
B=[length2*sin(theta2);-length2*cos(theta2);0;0];
返回omega数组(包含 omega3、velocity4、omega5、velocity6)
omega = A\(B*omega2);
求方程组的二阶导数

将上述一阶导数的方程组写成矩阵形式

在matlab中:
设A1阵
A1 = [-length3*sin(theta(1)),-1,0,0;
length3*cos(theta(1)),0,0,0;
0,1,-length5*sin(theta(2)),0;
0,0,length5*cos(theta(2)),-1];
设At阵
At = [-omega(1)*length3*cos(theta(1)),0,0,0;
-omega(1)*length3*sin(theta(1)),0,0,0;
0,0,-omega(3)*length5*cos(theta(2)),0;
0,0,-omega(3)*length5*sin(theta(2)),0];
设Bt阵
Bt = [omega2*length2*cos(theta2);omega2*length2*sin(theta2);0;0];
返回alpha数组(包含alpha3、alpha_line4、alpha5、alpha_line6)
alpha = A1\(-At*omega+omega2*Bt);
对杆组受力进行正交分解

将上述方程组写成矩阵形式

在matlab中:
设A2阵
A2=[sin(theta(2)),0,0,0;
-sin(theta(2)),1,sin(theta(1)),0,;
-cos(theta(2)),0,cos(theta(1)),0;
0,0,-length2*sin(theta2-theta(1)),28.19];
当 theta2 > 144*pi/180 && theta2 < 216*pi/180 的时候(在这个范围内滑块4受到向右的生产阻力227N)
设B2阵
B2=[alpha(4)*3.8/1000;0;alpha(2)*3.8/1000-227;0];
当其他的时候
设B2阵
B2=[alpha(4)*3.8/1000;0;alpha(2)*3.8/1000;0];
返回R数组(包含R45、R74、R23、R12)
R = A2\B2;
其中,数组R的第四项R(4)为R12
计算原动件齿轮一平衡力矩Mb
Mb=R(4)*r1
r1为齿轮一基圆半径
!!!其实不用高副低代,齿轮一给齿轮二的力矩等于R21对齿轮质心的力矩,所以齿轮二给齿轮一反作用一个力矩,大小和上述力矩相等,对于齿轮一而言,平衡力矩Mb就是用来平衡这个反作用的力矩的,所以大小相等。
接下来是matlab代码
函数一
%函数1 function f=pos_6a(theta,theta2,length2,length3,length5,L) f(1)=length2*cos(theta2)+length3*cos(theta(1))-theta(3); f(2)=length2*sin(theta2)+length3*sin(theta(1)); f(3)=length5*cos(theta(2))-L+theta(3); f(4)=length5*sin(theta(2))-theta(4); end % theta3=theta(1); % theta5=theta(2); % length4=theta(3); % length6=theta(4);函数二(调用了函数一)
%函数2 function output = analysis_data_6a(theta2,omega2,length2,length3,length5,L) options=optimset('display','off'); %x0=[0,0,0,0]; x0=[170.98*pi/180,156.51*pi/180,-138.94/2,-52.62/2]; %返回位移 theta=fsolve(@pos_6a,x0,options,theta2,length2,length3,length5,L); % 计算角速度 omega A=[-length3*sin(theta(1)),-1,0,0; length3*cos(theta(1)),0,0,0; 0,1,-length5*sin(theta(2)),0; 0,0,length5*cos(theta(2)),-1]; B=[length2*sin(theta2);-length2*cos(theta2);0;0]; omega = A\(B*omega2); % 计算角加速度alpha A1 = [-length3*sin(theta(1)),-1,0,0; length3*cos(theta(1)),0,0,0; 0,1,-length5*sin(theta(2)),0; 0,0,length5*cos(theta(2)),-1]; At = [-omega(1)*length3*cos(theta(1)),0,0,0; -omega(1)*length3*sin(theta(1)),0,0,0; 0,0,-omega(3)*length5*cos(theta(2)),0; 0,0,-omega(3)*length5*sin(theta(2)),0]; Bt = [omega2*length2*cos(theta2);omega2*length2*sin(theta2);0;0]; alpha = A1\(-At*omega+omega2*Bt); if theta2 > 144*pi/180 && theta2 < 216*pi/180 %求解力 A2=[sin(theta(2)),0,0,0; -sin(theta(2)),1,sin(theta(1)),0,; -cos(theta(2)),0,cos(theta(1)),0; 0,0,-length2*sin(theta2-theta(1)),28.19]; B2=[alpha(4)*3.8/1000;0;alpha(2)*3.8/1000-227;0]; R = A2\B2; else A2=[sin(theta(2)),0,0,0; -sin(theta(2)),1,sin(theta(1)),0,; -cos(theta(2)),0,cos(theta(1)),0; 0,0,-length2*sin(theta2-theta(1)),28.19]; B2=[alpha(4)*3.8/1000;0;alpha(2)*3.8/1000;0]; R = A2\B2; disp(R); end output = {theta, omega, alpha,R}; end主函数)(求解了滑块4、6的位移、速度、加速度以及齿轮一的平衡力偶,并输出曲线)
%主函数 length2=24; length3=90; length5=66; L=-130; omega2 = 4*pi; alpha2 = 0; hd = pi/180; du = 180/pi; disp('继续'); %定义有361个元素0的数组 theta3 = zeros(1, 361); theta5 = zeros(1, 361); length4 = zeros(1, 361); length6 = zeros(1, 361); omega3 = zeros(1, 361); omega5 = zeros(1, 361); velocity4 = zeros(1, 361); velocity6 = zeros(1, 361); R45 = zeros(1, 361); R74 = zeros(1, 361); R23 = zeros(1, 361); R12 = zeros(1, 361); Mb = zeros(1, 361); %调用函数计算六杆机构的位移、速度、加速度 for n1 = 1:361 theta2 = (n1-1)*hd; % 将角度转换为弧度制 output = analysis_data_6a(theta2,omega2,length2,length3,length5,L); theta = output{1}; % 获取theta数组 omega = output{2}; alpha = output{3}; R = output{4}; theta3(n1) = theta(1); % 杆3的角位移 theta5(n1) = theta(2); % 杆5的角位移 length4(n1) = theta(3); % 杆4的位移 length6(n1) = theta(4); omega3(n1) = omega(1); % 杆2的角速度 velocity4(n1) = omega(2); % 杆4的角速度 omega5(n1) = omega(3); % 杆5的角位移 velocity6(n1) = omega(4); alpha3(n1) = alpha(1); % 杆3的角加速度 alpha_line4(n1) = alpha(2); % 滑块4的加速度 alpha5(n1) = alpha(3); % 杆5的角加速度 alpha_line6(n1) = alpha(4); % 滑块6的加速度 R45(n1)=R(1); R74(n1)=R(2); R23(n1)=R(3); R12(n1)=R(4); %N Mb(n1)=R12(n1)*9.485/1000; %N*m end n1 = 1:361; subplot(2,2,1); plot(n1,length4,'b',n1,length6,'k','LineWidth',2); % 滑块4、6位移随角度变化 xlabel('齿轮二转角 \theta1/\circ'); ylabel('滑块4、6的线位移/mm'); legend('线位移4','线位移6'); grid on; hold on; subplot(2,2,2); %滑块4、6速度变化 plot(n1,velocity4,'b',n1,velocity6,'k'); xlabel('齿轮二转角 \theta1/\circ'); ylabel('滑块4、6速度/ mm\cdots^{-1}'); legend('速度4','速度6'); grid on; hold on; subplot(2,2,3); %滑块4、6加速度变化 plot(n1, alpha_line4,'b',n1,alpha_line6,'k'); xlabel('齿轮二转角 \theta1/\circ'); ylabel('滑块4、6加速度/ mm\cdots^{-2}'); legend('加速度4','加速度6'); grid on; hold on; subplot(2,2,4); %平衡力矩变化(空载和有载) plot(n1, Mb,'b'); xlabel('齿轮二转角 \theta1/\circ'); ylabel('齿轮一(原动件)平衡力矩/ N*m'); legend('平衡力矩'); grid on; hold on; 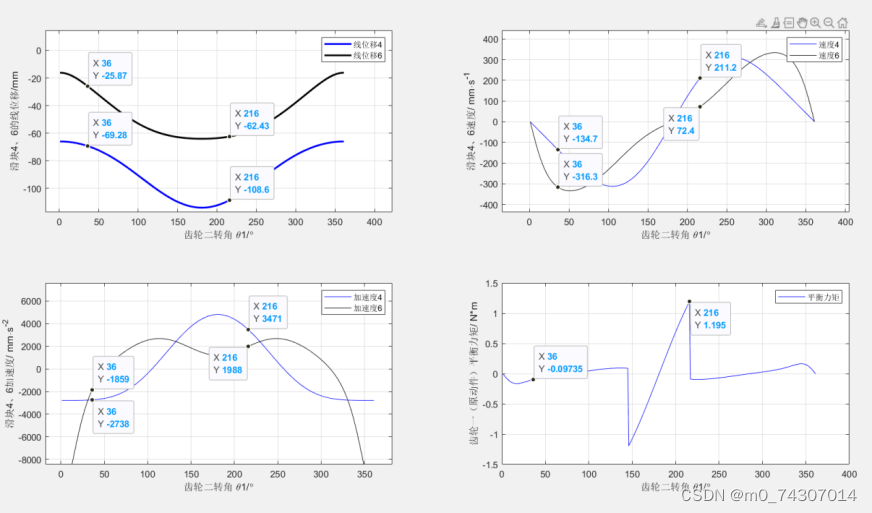
接下来是解析法和图解法的结果对比(我们组10个人)
length4=[-66,-66.7,-69.47,-73.78,-79.64,-86.74,-94.47,-101.99,-108.3,-112.63,-114,-112.5,-108.3,-102,-94.48,-86.74,-79.64,-73.78,-69.47,-66.68]; length6=[-16.13,-19.4,-26.31,-34.59,-42.66,-49.85,-55.62,-59.76,-62.33,-63.48,-64.03,-63.33,-62.33,-59.76,-55.63,-49.85,-42.66,-34.57,-26.31,-19.25]; velocity4=[0,-68.7,-138.4,-204.7,-262.24,-301.6,-315.4,-283,-201,-113,0,116.82,215.9,283,310.96,301.6,262.3,204.7,152.2,68.1]; velocity6=[0,-225.32,-318.48,-333,-310.32,-261.7,-202.6,-132.7,-69.4,-31.4,0,32,25.12,132.6,201.92,261.7,312.1,333,336.7,225.7]; alpha_line4=[-2779.3,-3208.8,-2730.5,-2677.5,-2217.5,-1048.5,335,1918.5,3838.9,4431.5,5014.3,4446.8,3395.5,1923.5,332.5,-1048.5,-2062,-2527,-2432.5,-2762]; alpha_line6=[-11031.8,-7782,-1701.5,311.5,1257,2330.8,2817,2534,2044,1016.5,1227,1682,2018.5,2536,2694.5,2330.8,1462,310.5,-1995,-4547]; Mb=[0,-0.8400924, -0.093,-0.0404,-0.003,0.0226,0.0800,0.08865356875, 0.088, -0.736 ,0,1.61536,1.25,-0.0900,-0.059,-0.0246,0.1101,0.0625941875,0.093, 0.139 ]; n1 = 0:19; n1=n1*1/20*360; subplot(2,2,1); plot(n1,length4,'r',n1,length6,'y'); % 滑块4、6位移随角度变化 xlabel('齿轮二转角 \theta1/\circ'); ylabel('滑块4、6的线位移/mm'); legend('线位移4','线位移6'); grid on; hold on; subplot(2,2,2); %滑块4、6速度变化 plot(n1,velocity4,'r',n1,velocity6,'y'); xlabel('齿轮二转角 \theta1/\circ'); ylabel('滑块4、6速度/ mm\cdots^{-1}'); legend('速度4','速度6'); grid on; hold on; subplot(2,2,3); %滑块4、6加速度变化 plot(n1, alpha_line4,'r',n1,alpha_line6,'y'); xlabel('齿轮二转角 \theta1/\circ'); ylabel('滑块4、6加速度/ mm\cdots^{-2}'); legend('加速度4','加速度6'); grid on; hold on; subplot(2,2,4); %原动件平衡力矩变化 plot(n1,Mb,'r'); xlabel('齿轮二转角 \theta1/\circ'); ylabel('齿轮一(原动件)平衡力矩/ N*m'); legend('平衡力矩'); grid on; hold on; F5运行主函数,再F5运行对比的代码,结果如下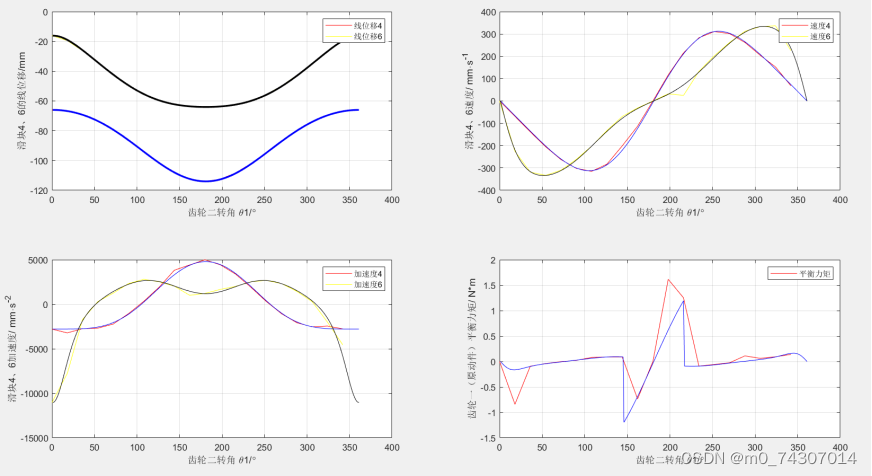
然后是我个人的误差分析

误差原因:(希望可以指出我这里面的错误和不足,原因真的不会写)
- 初始值选择有偏差:fsolve函数需要提供一个初始的猜测解来开始求解过程,我们给出的初始值是caxa在36°位置的测量结果,测量结果存在误差,因此解析法的结果与理论计算存在误差。
- Matlab矩阵计算与理论计算值存在微小误差。
- Caxa绘图测量长度存在误差。
- 图解法过程中VD、aD、ω3、ω5的瞬心法的半径测量值有误差。
- π值保留位数有误差。
