代码随想录–回溯部分
day 23 回溯部分第二天
文章目录
一、力扣39–组合总和
代码随想录题目链接:代码随想录
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
其实和之前的组合总和一样,只是多了个可以重复选取,那么在回溯的时候startIndex不需要加一即可
代码如下:
class Solution { public: int sum = 0; vector<int> path; vector<vector<int>> result; void backTracking(vector<int> candidates, int target, int start) { if(sum > target)return; else if (sum == target) { result.push_back(path); return; } for(int i = start; i < candidates.size(); i ++) { sum += candidates[i]; path.push_back(candidates[i]); backTracking(candidates, target, i); sum -= candidates[i]; path.pop_back(); } } vector<vector<int>> combinationSum(vector<int>& candidates, int target) { backTracking(candidates, target, 0); return result; } }; 二、力扣40–组合总和Ⅱ
代码随想录题目链接:代码随想录
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
其实就是多了个要求:答案去重,粗暴做肯定会超时
所以使用新的数组used来记录每个元素是否被使用过,如果使用过了就跳过
这点有些像力扣15三数之和的去重,应当比较candidates [i]和[i-1]是否一样,一样就把i跳过,因为这样跳过的是搜索过的元素
同时还要通过used来判断目前是同层还是不同层
如果是true,说明这个重复的值是上层递归的,那就可以取,如果为false,说明是同层递归,那再取就会重复了
代码如下:
class Solution { public: int sum = 0; vector<int> path; vector<vector<int>> result; vector<bool> used; void backTracking(vector<int> candidates, int target, int start) { if(sum > target)return; else if (sum == target) { result.push_back(path); return; } for(int i = start; i < candidates.size(); i ++) { if(i > 0 && candidates[i] == candidates[i-1] && used[i - 1] == false)continue; sum += candidates[i]; path.push_back(candidates[i]); used[i] = true; backTracking(candidates, target, i+1); sum -= candidates[i]; path.pop_back(); used[i] = false; } } vector<vector<int>> combinationSum2(vector<int>& candidates, int target) { used = vector<bool>(candidates.size(), false); sort(candidates.begin(), candidates.end()); backTracking(candidates, target, 0); return result; } }; 还是挺抽象的,借助used来表示递归的层数,或许用栈能够更直白一些?
三、力扣–分割回文串
代码随想录题目链接:代码随想录
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
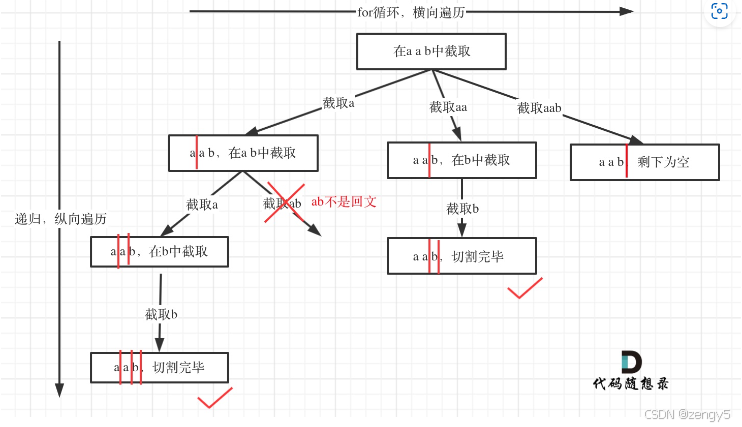
照着图写就行
代码如下:
class Solution { public: vector<vector<string>> result; vector<string> path; bool isPalindrome(const string& s, int start, int end) { for (int i = start, j = end; i < j; i++, j--) { if (s[i] != s[j]) return false; } return true; } void backTracking(string s, int startIndex) { if (startIndex >= s.size()) { result.push_back(path); return; } for(int i = startIndex; i < s.size(); i++) { if(isPalindrome(s, startIndex, i)) { string temp = s.substr(startIndex, i - startIndex + 1); path.push_back(temp); } else continue; backTracking(s, i + 1); path.pop_back(); } } vector<vector<string>> partition(string s) { backTracking(s, 0); return result; } }; 值得一讲的是在回溯前的处理,并不是每个遍历都值得接着向下回溯,实际上如果本次搜索并不是回文串,就可以结束了
因为结果中必须都是回文串,所以一直要搜索到回文串后,才有资格接着向下搜索。