二分查找的时间与空间，算法好坏衡量

时间复杂度，算法好坏衡量

定义

用于衡量一个算法的执行，随数据规模增大，而增长的时间成本。（不依赖环境因素）

具体表现

假设算法要处理的数据规模是n，代码总的执行行数用f(n)来表示。

比如：

线性查找算法函数f(n)= 3*n+3

二分查找算法函数f(n)=(floor(log_2(n))+1)*5+4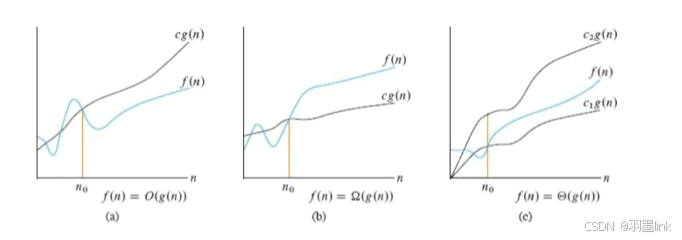

如上分别是：渐进上界O(g(n))，渐进下界O(Ω(n))，渐进紧界 c,c1,c2都是常数 f(n)实质性代码行数与n的函数 g(n)是经过化简，变化趋势与f(n)一致的函数 

渐进上界

举例

线性查找:

f(n)=3*n+3  g(n)=n(把原函数f(n)拆开当做多项式，最高项就是g(n))  若取c=4，在n=3之后g(n)可以作为原函数f(n)的渐进上界，那么就可以写作O(n)。 

二分查找:

f(n)=5*floor(log_2(n))+9 g(n)=log_2(n) O(log_2(n)) 

规则

$$对于f(n)来说，求g(n)1，表达式中相乘的常量可以省略，比如上文线性查找：3\ast n，3可以省略，因为函数g(n)总是要乘一个常数。2，多项式中数量规模更小的(低次项)的表达式，比如存在：n^2+n,那么则忽略n。3，不同底数的对数，渐进上界可以用一个对数函数lo{g}_2(n)表示，比如：存在函数lo{g}_2(n),可以被替换为lg(n)，因为lo{g}_2(n)=lg(n)/lg(2),相乘的常量1/lg(2)可以省略。这步是换底公式lo{g}_{a}b=lo{g}_{c}b/lo{g}_{c}a。4，对数的常数次幂可以省略，比如log(n^c)=c\ast log(n)$$

常见算法大O表示

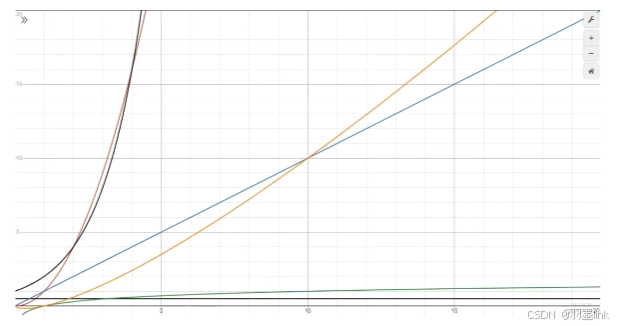
黑色横线O(1):常量时间，算法不随着数据规模而变化 绿色O(log(n)):对数时间 蓝色O(n)，线性时间没算法时间与数据规模成正比 橙色O(n*log(n)),拟线性时间，相近线性时间 红色O(n^2)，平方时间 黑色朝上O(2_n)，指数时间 未画出的O(n!)，巨大变化，最高时间复杂度 

渐进下界

下方线表示该算法的最优情况，从某个常数n_0开始，cg(n)就一直处于f(n)下方，那么记作Ω(g(n))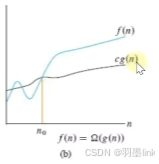

渐进紧界

从某个常数n开始，f(n)总是处于c1 * g(n)与c2 * g(n)之间，那么记作θ(g(n))，既能代表该代码执行的最优情况也可以代表最差情况。(注意这个符号念xi 二声 ta 一声)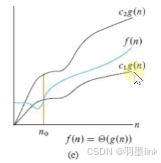

空间复杂度，算法好坏衡量

定义

与时间复杂度类似，一般也是用大O表示发来衡量：一个算法执行随数据规模增大，而增长的额外占用空间成本

具体表现

举例

    private static int binarySearchBasic(int[] a,int target){         //不看原始数据，看新增，这里不看“int[] a,int target”         int i = 0,j = a.length - 1;         //这里i和j指针各占4字节         while(i<=j){             int m = (i + j) / 2;             if (target < a[m]){                 j = m - 1;//目标小于中间值             } else if(target > a[m]){                 i = m + 1;//目标大于中间值             }else{                 return m;             }         }         //循环占用4字节(m)         return -1;     } 

$$总计12字节也就是o(1),常量时间，不会随着n的变化而变化。$$

二分查找性能分析

时间复杂度

最坏情况：O(log n)

最好情况：如果待查找元素恰好在数组中央，只需要循环一次O(1)

空间复杂度

计12字节也就是o(1),常量时间，不会随着n的变化而变化。
$$

二分查找性能分析

时间复杂度

最坏情况：O(log n)

最好情况：如果待查找元素恰好在数组中央，只需要循环一次O(1)

空间复杂度

需要常数个指针i，j，m，因此额外占用的空间是O(1)。