阅读量:4
文章目录
题目解析
给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于等于 target 的长度最小的
子数组
[numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
解题思路
暴力解法,我们可以找出所有的子数组,然后再求解。但是时间复杂度高,不适合。不过我们在子数组的过程可以发现一些规律,得到一些优化。例如 nums = [2,3,1,2,4,3],target = 7,当我们找到子数组[2,3,1,2],这个子数组已经满足里题目要求,如果我们再在这个子数组的基础上向后遍历加上其他数字变为[2,3,1,2,4],(正整数的数组)虽然同样也满足题目要求但数组长度明显会大于前一个数组,所以这样的子数组我们应该排除掉。直接找满足target的最小数组就可以了。
这种用同向指针(两个指针同时向前或后移动),方法有个名字叫滑动窗口。
代码实现
Java实现
class Solution { public int minSubArrayLen(int target, int[] nums) { int n=nums.length; int i=0,j=0,sum=0; int length=1000000; int ret=0; while(j<n) { sum=sum+nums[j]; while(sum>=target) { ret=j-i+1; length=Math.min(length,ret); sum=sum-nums[i++]; } j++; } if(ret==0) { return 0; } return length; } } 解释代码
int n = nums.length; int i = 0, j = 0; // i 和 j 分别表示子数组的起始和结束位置 int sum = 0; // sum 表示当前子数组的和 int length = 1000000; // 初始化一个较大的长度值,用于记录最短子数组的长度 int ret = 0; // ret 用于记录当前子数组的长度 while (j < n) { sum = sum + nums[j]; while (sum >= target) { ret = j - i + 1; // 计算当前子数组的长度 length = Math.min(length, ret); // 更新最短子数组的长度 sum = sum - nums[i++]; // 移动左指针,缩小子数组范围,更新和 } j++; // 移动右指针,扩大子数组范围 } if (ret == 0) { return 0; // 如果没有找到满足条件的子数组,返回 0 } return length; // 返回最短子数组的长度 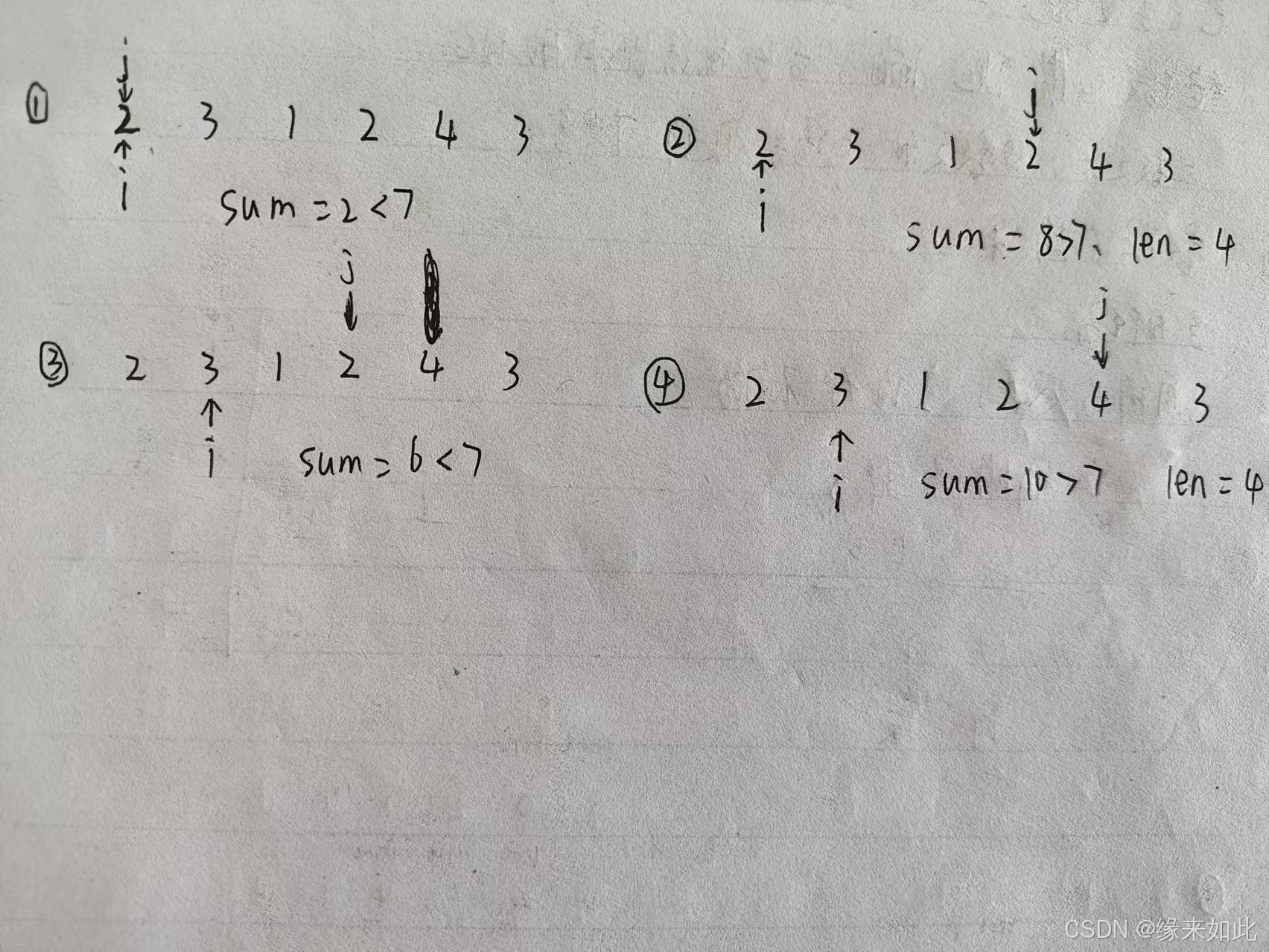
C语言实现
int minSubArrayLen(int target, int* nums, int numsSize) { int i=0; int j=0; int sum=0; int ret=INT_MAX; int length=0; for(j=0;j<numsSize;j++) { sum+=nums[j]; while(sum>=target) { length=j-i+1; ret=ret>length?length:ret; sum=sum-nums[i++]; } } if(length==0) { return 0; } else { return ret; } } 感谢您的阅读,欢迎评论,点赞,你们的支持就是对我最大的鼓励。
