【算法笔记自学】第 11 章 提高篇（5）——动态规划专题

avatar
作者
猴君
阅读量:0

11.1动态规划的递归写法和递推写法

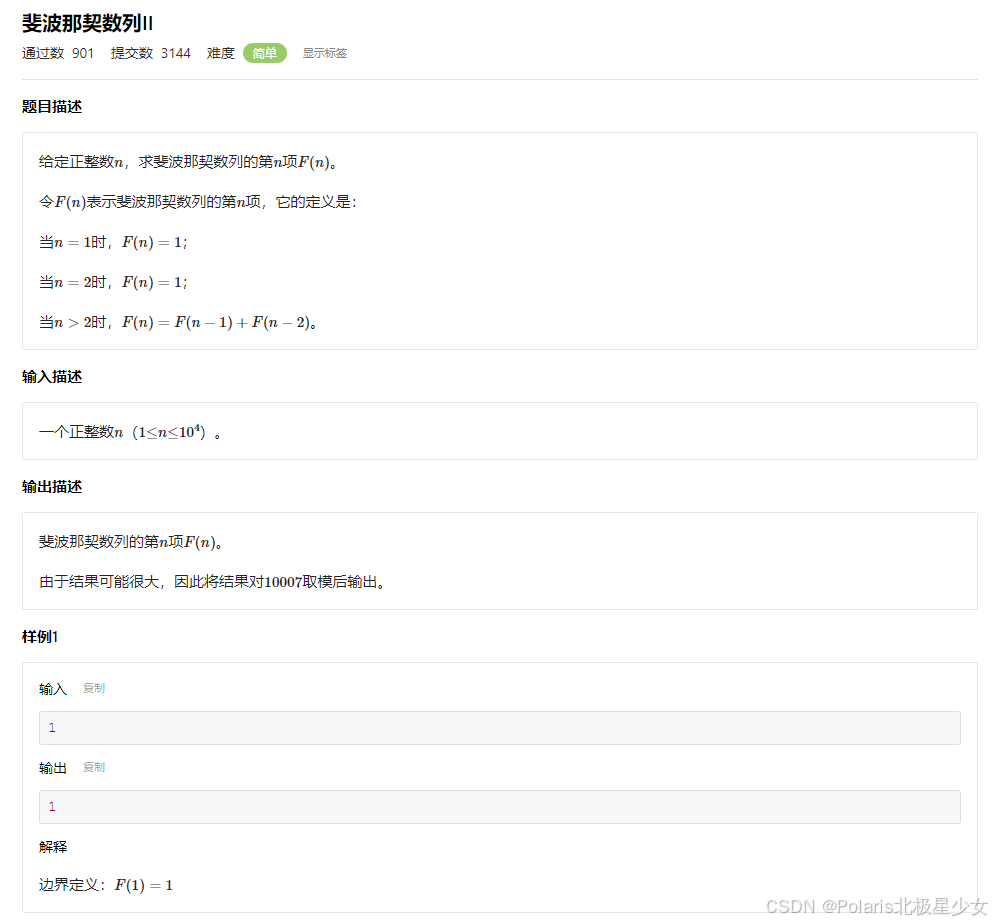
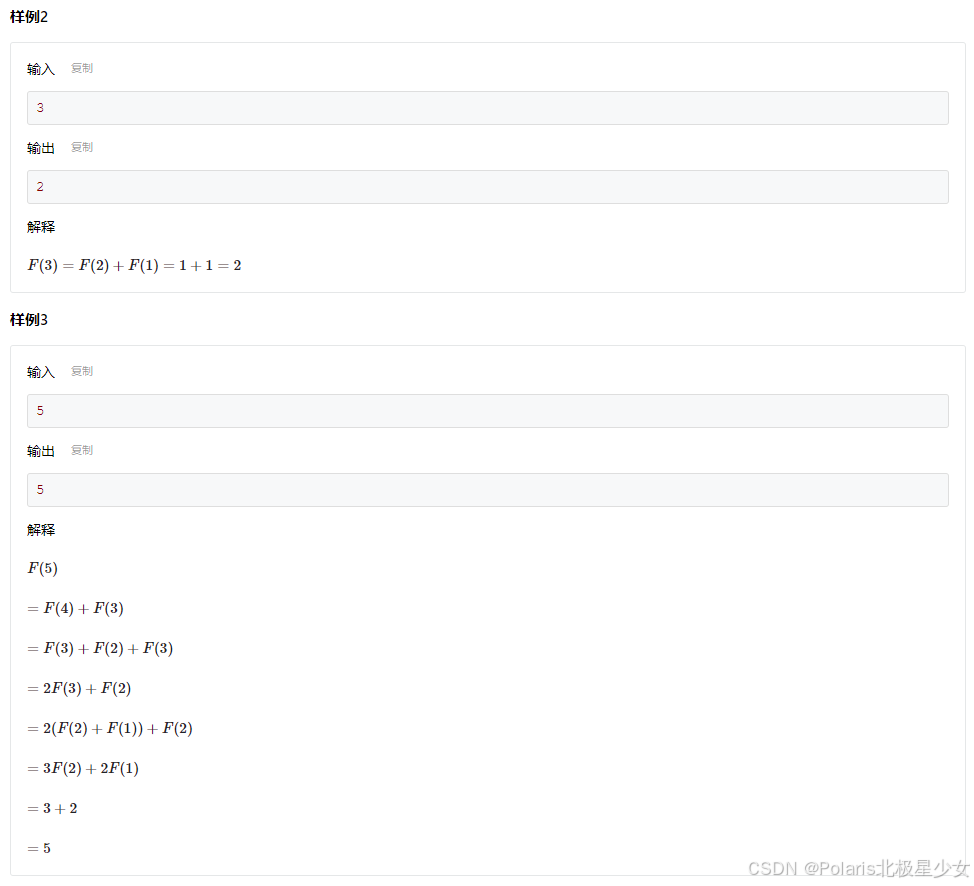
#include <cstdio>  const int MOD = 10007; const int MAXN = 10000 + 1; int fib[MAXN];  int main() {     int n;     scanf("%d", &n);     fib[1] = fib[2] = 1;     for (int i = 3; i <= n; i++) {         fib[i] = (fib[i - 1] + fib[i - 2]) % MOD;     }     printf("%d", fib[n]);     return 0; }

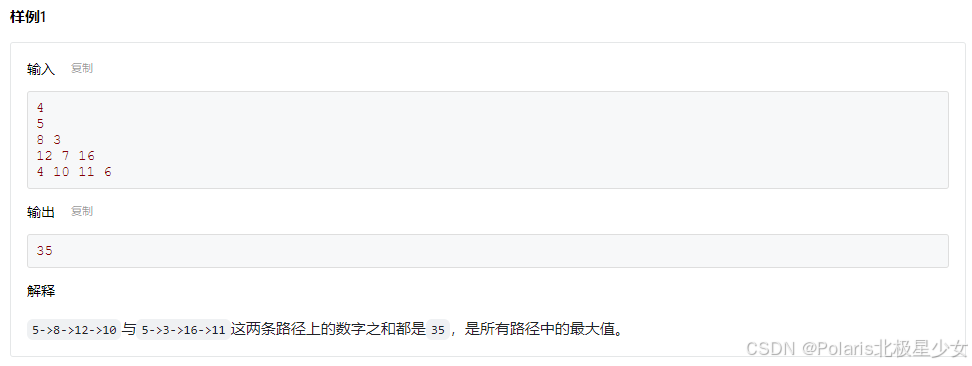
#include <cstdio> #include <algorithm> using namespace std;  const int MAXN = 100 + 1; int a[MAXN][MAXN]; int dp[MAXN][MAXN];  int main() {     int n;     scanf("%d", &n);     for (int i = 1; i <= n; i++) {         for (int j = 1; j <= i; j++) {             scanf("%d", &a[i][j]);         }     }     for (int i = 1; i <= n; i++) {         dp[n][i] = a[n][i];     }     for (int i = n - 1; i >= 1; i--) {         for (int j = 1; j <= i; j++) {             dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + a[i][j];         }     }     printf("%d", dp[1][1]);     return 0; }

11.2最大连续子序列和

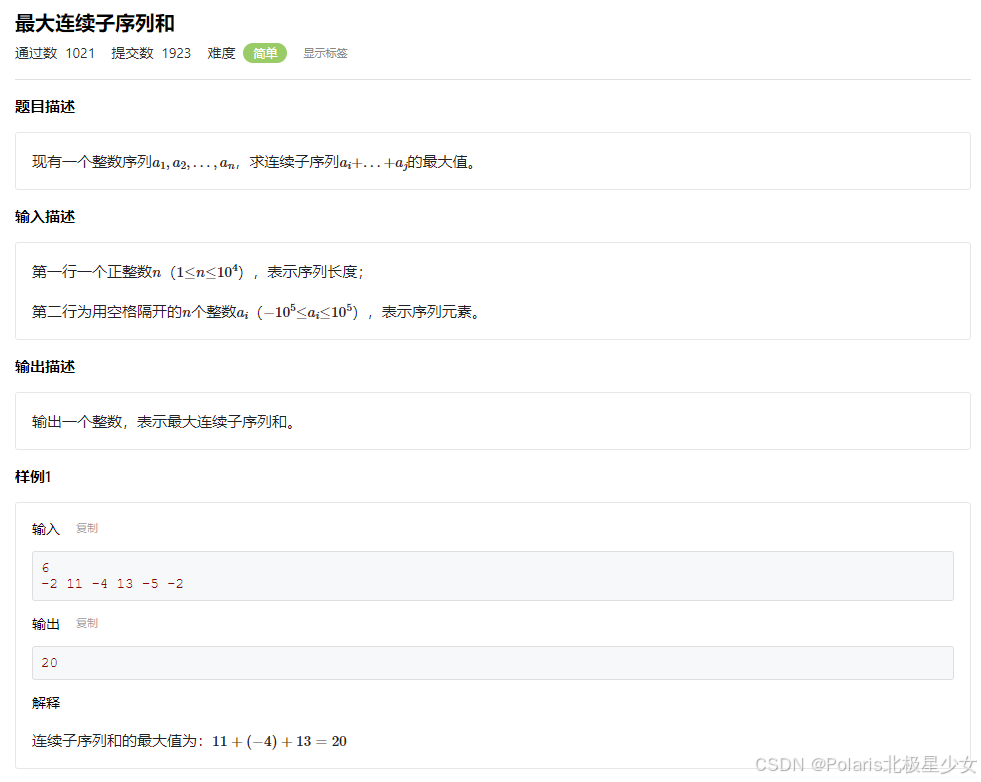
#include <cstdio> #include <algorithm> using namespace std;  const int MAXN = 10000; const int INF = 0x3fffffff; int a[MAXN]; int dp[MAXN];  int main() {     int n;     scanf("%d", &n);     for (int i = 0; i < n; i++) {         scanf("%d", &a[i]);     }     dp[0] = a[0];     for (int i = 1; i < n; i++) {         dp[i] = max(a[i], dp[i - 1] + a[i]);     }     int maxResult = -INF;     for (int i = 0; i < n; i++) {         maxResult = max(maxResult, dp[i]);     }     printf("%d", maxResult);     return 0; }

11.3最长不下降子序列（LIS）

 

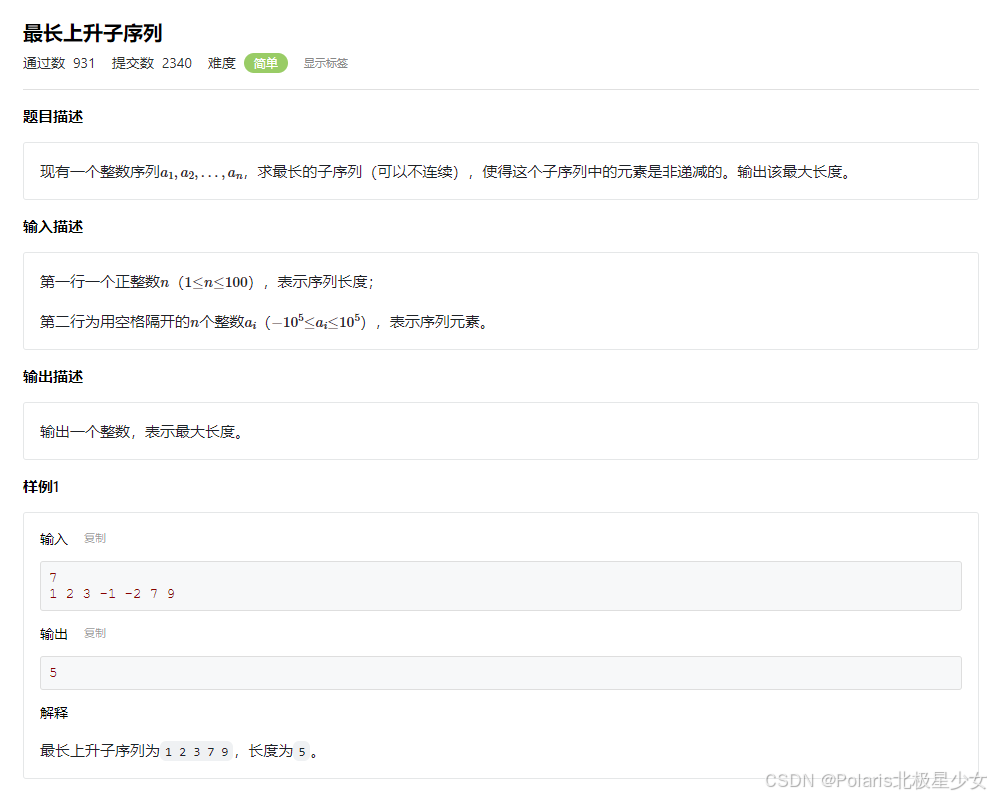
#include <cstdio> #include <algorithm> using namespace std;  const int MAXN = 100; int a[MAXN]; int dp[MAXN];  int main() {     int n;     scanf("%d", &n);     for (int i = 0; i < n; i++) {         scanf("%d", &a[i]);     }     int maxLen = 0;     for (int i = 0; i < n; i++) {         dp[i] = 1;         for (int j = 0; j < i; j++) {             if (a[j] <= a[i] && dp[j] + 1 > dp[i]) {                 dp[i] = dp[j] + 1;             }         }         maxLen = max(maxLen, dp[i]);     }     printf("%d", maxLen);     return 0; }

11.4最长公共子序列（LCS）

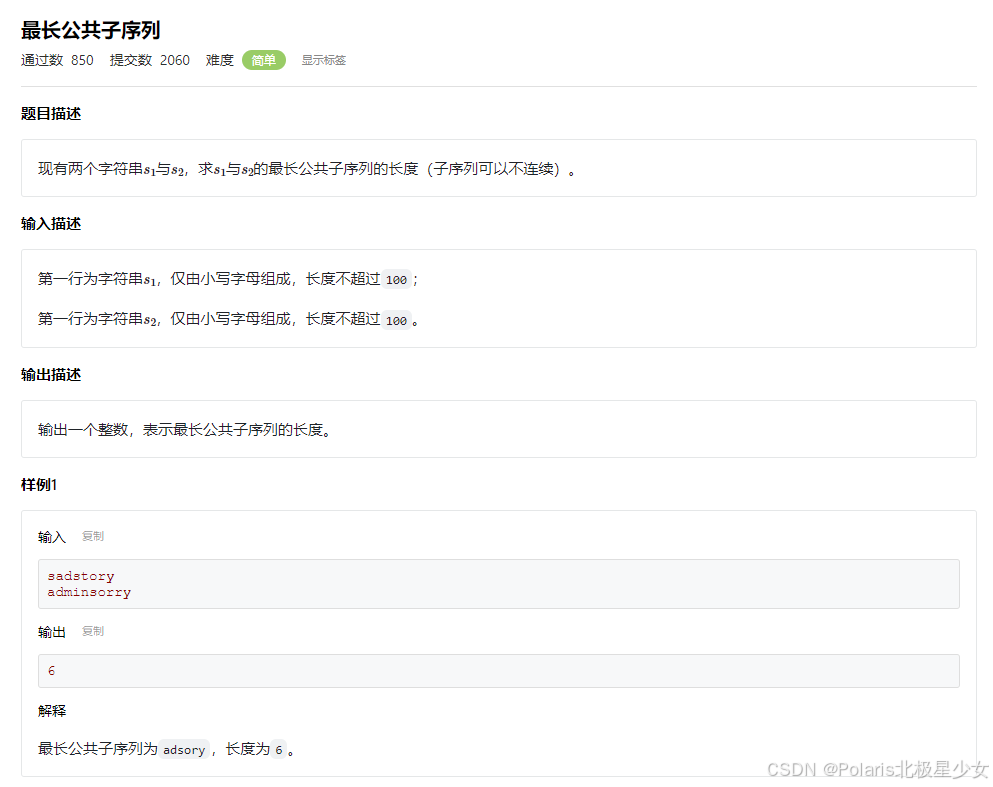
#include <iostream> #include <string> #include <algorithm> using namespace std;  const int MAXN = 100 + 1; int dp[MAXN][MAXN];  int main() {     string s1, s2;     cin >> s1 >> s2;     for (int i = 1; i <= s1.length(); i++) {         for (int j = 1; j <= s2.length(); j++) {             if (s1[i - 1] == s2[j - 1]) {                 dp[i][j] = dp[i - 1][j - 1] + 1;             } else {                 dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);             }         }     }     printf("%d", dp[s1.length()][s2.length()]);     return 0; }

11.5最长回文子串

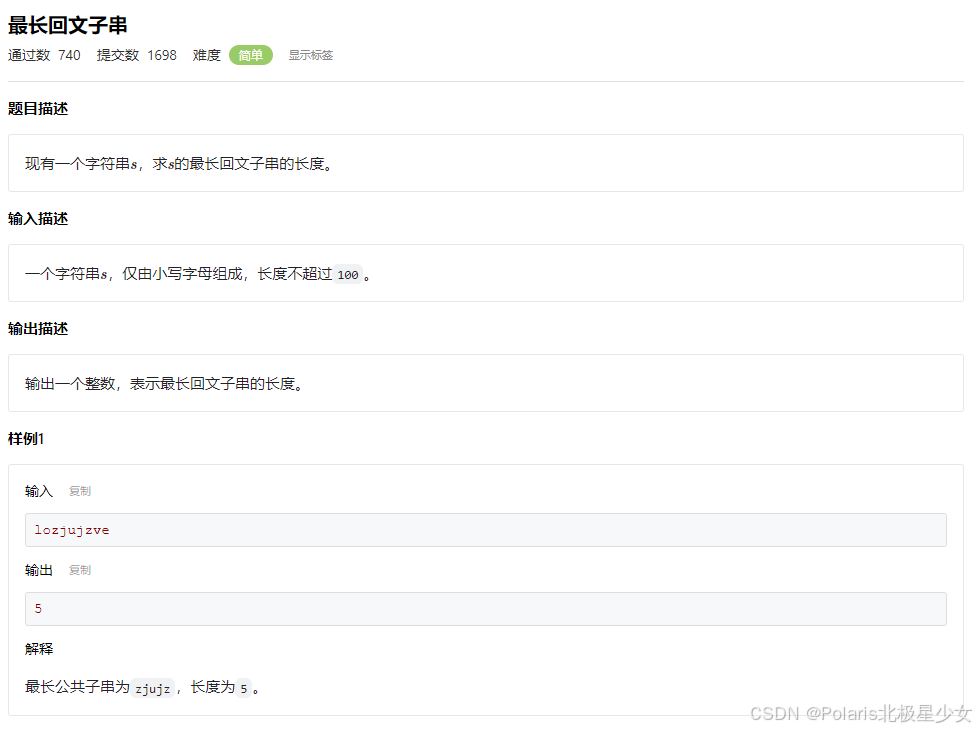
#include <iostream> #include <cstring> #include <string> using namespace std;  const int MAXN = 100; bool dp[MAXN][MAXN];  int main() {     string s;     cin >> s;     int maxLength = 1;     memset(dp, false, sizeof(dp));     for (int i = 0; i < s.length(); i++) {         dp[i][i] = true;     }     for (int i = 0; i < (int)s.length() - 1; i++) {         if (s[i] == s[i + 1]) {             dp[i][i + 1] = true;             maxLength = 2;         }     }     for (int len = 3; len <= s.length(); len++) {         for (int i = 0; i + len - 1 < s.length(); i++) {             int j = i + len - 1;             if (s[i] == s[j] && dp[i + 1][j - 1]) {                 dp[i][j] = true;                 maxLength = len;             }         }     }     printf("%d", maxLength);     return 0; }

11.6DAG最长路

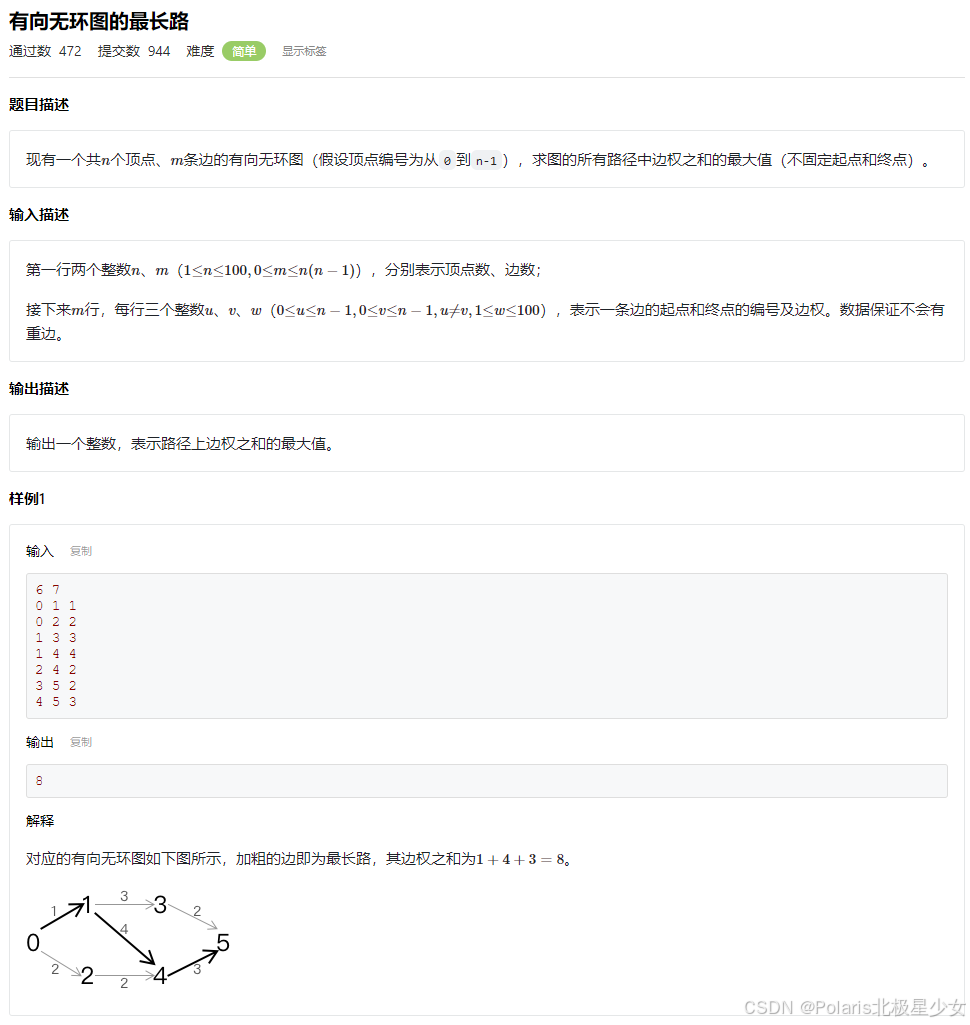
#include <cstdio> #include <cstring> #include <algorithm> using namespace std;  const int MAXN = 100; const int INF = 1e9; int G[MAXN][MAXN]; int dp[MAXN];  int getDAGMaxLength(int i, int n) {     if (dp[i]) {         return dp[i];     }     for (int j = 0; j < n; j++) {         if (G[i][j] != INF) {             dp[i] = max(dp[i], getDAGMaxLength(j, n) + G[i][j]);         }     }     return dp[i]; }  int main() {     memset(dp, 0, sizeof(dp));     fill(G[0], G[0] + MAXN * MAXN, INF);     int n, m;     scanf("%d%d", &n, &m);     int u, v, w;     for (int i = 0; i < m; i++) {         scanf("%d%d%d", &u, &v, &w);         G[u][v] = w;     }     int maxLength = 0;     for (int i = 0; i < n; i++) {         maxLength = max(maxLength, getDAGMaxLength(i, n));     }     printf("%d", maxLength);     return 0; }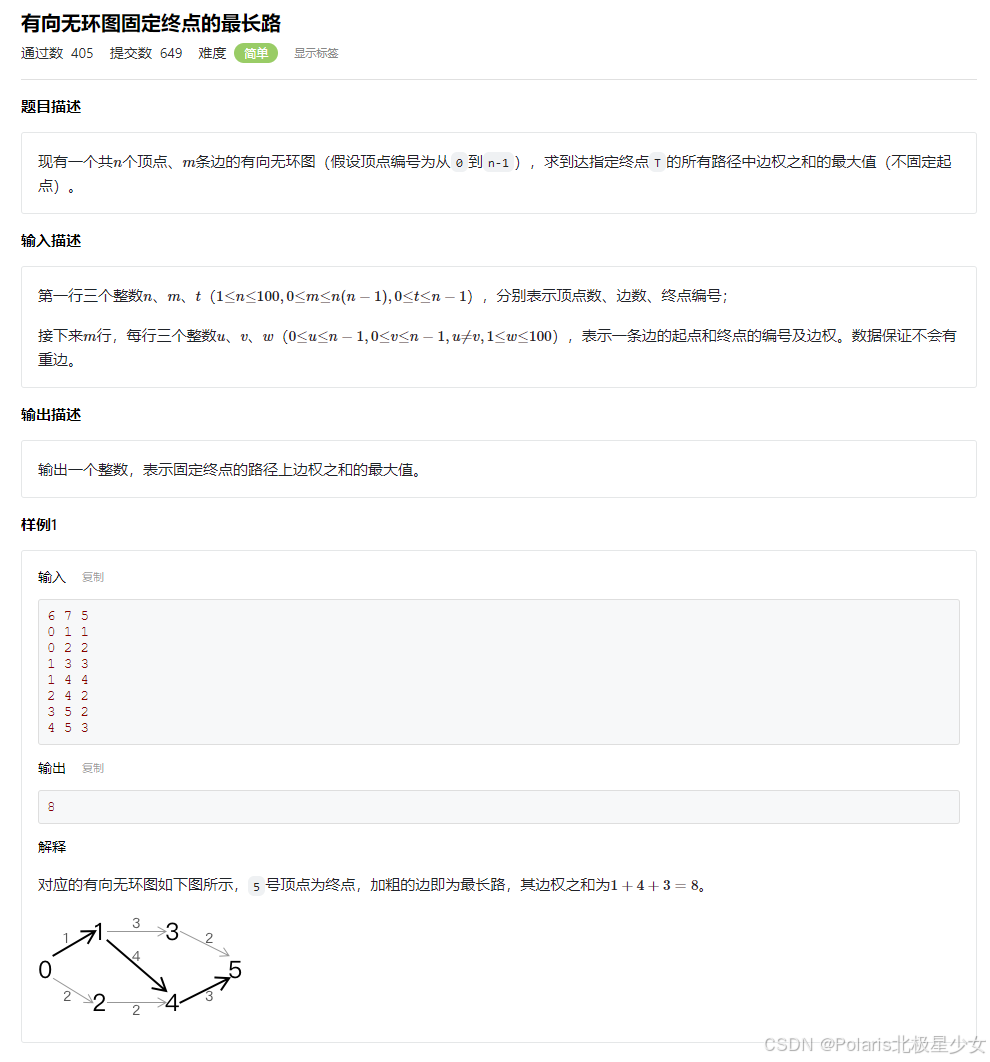

#include <cstdio> #include <cstring> #include <algorithm> using namespace std;  const int MAXN = 100; const int INF = 1e9; int G[MAXN][MAXN]; int dp[MAXN];  int getDAGMaxLength(int i, int n) {     if (dp[i] >= 0) {         return dp[i];     }     for (int j = 0; j < n; j++) {         if (G[i][j] != INF) {             dp[i] = max(dp[i], getDAGMaxLength(j, n) + G[i][j]);         }     }     return dp[i]; }  int main() {     fill(dp, dp + MAXN, -INF);     fill(G[0], G[0] + MAXN * MAXN, INF);     int n, m, t;     scanf("%d%d%d", &n, &m, &t);     dp[t] = 0;     int u, v, w;     for (int i = 0; i < m; i++) {         scanf("%d%d%d", &u, &v, &w);         G[u][v] = w;     }     int maxLength = 0;     for (int i = 0; i < n; i++) {         maxLength = max(maxLength, getDAGMaxLength(i, n));     }     printf("%d", maxLength);     return 0; }

11.7背包问题

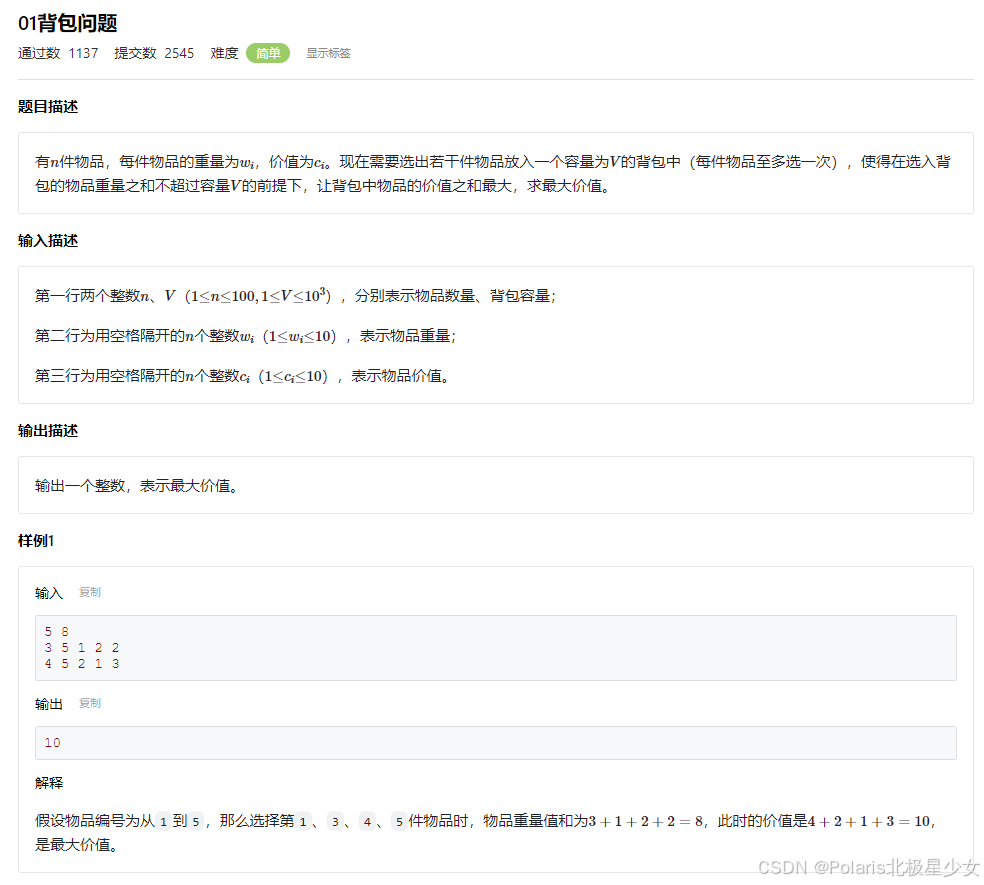
#include <cstdio> #include <cstring> #include <algorithm> using namespace std;  const int MAXN = 100 + 1; const int MAXV = 1000 + 1; int w[MAXN], c[MAXN]; int dp[MAXV];  int main() {     int n, maxW;     scanf("%d%d", &n, &maxW);     for (int i = 1; i <= n; i++) {         scanf("%d", &w[i]);     }     for (int i = 1; i <= n; i++) {         scanf("%d", &c[i]);     }     memset(dp, 0, sizeof(dp));     for (int i = 1; i <= n; i++) {         for (int v = maxW; v >= w[i]; v--) {             dp[v] = max(dp[v], dp[v - w[i]] + c[i]);         }     }     printf("%d", dp[maxW]);     return 0; }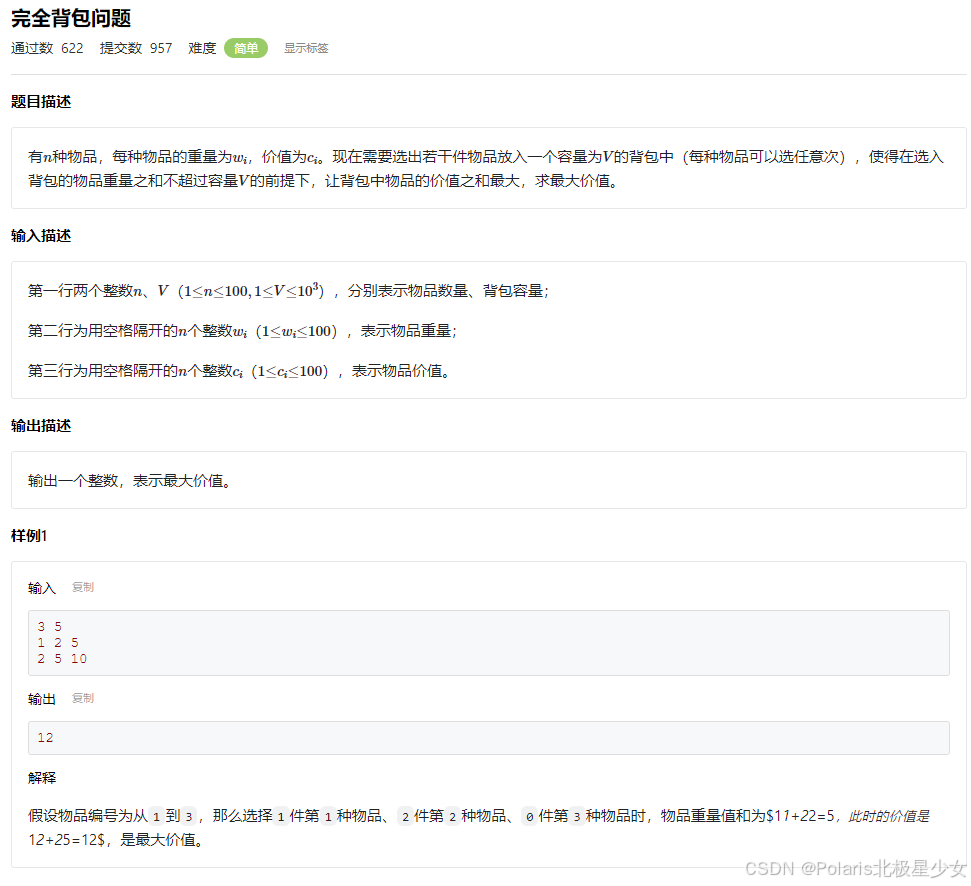

#include <cstdio> #include <cstring> #include <algorithm> using namespace std;  const int MAXN = 100 + 1; const int MAXV = 1000 + 1; int w[MAXN], c[MAXN]; int dp[MAXV];  int main() {     int n, maxW;     scanf("%d%d", &n, &maxW);     for (int i = 1; i <= n; i++) {         scanf("%d", &w[i]);     }     for (int i = 1; i <= n; i++) {         scanf("%d", &c[i]);     }     memset(dp, 0, sizeof(dp));     for (int i = 1; i <= n; i++) {         for (int v = w[i]; v <= maxW; v++) {             dp[v] = max(dp[v], dp[v - w[i]] + c[i]);         }     }     printf("%d", dp[maxW]);     return 0; }

11.8总结

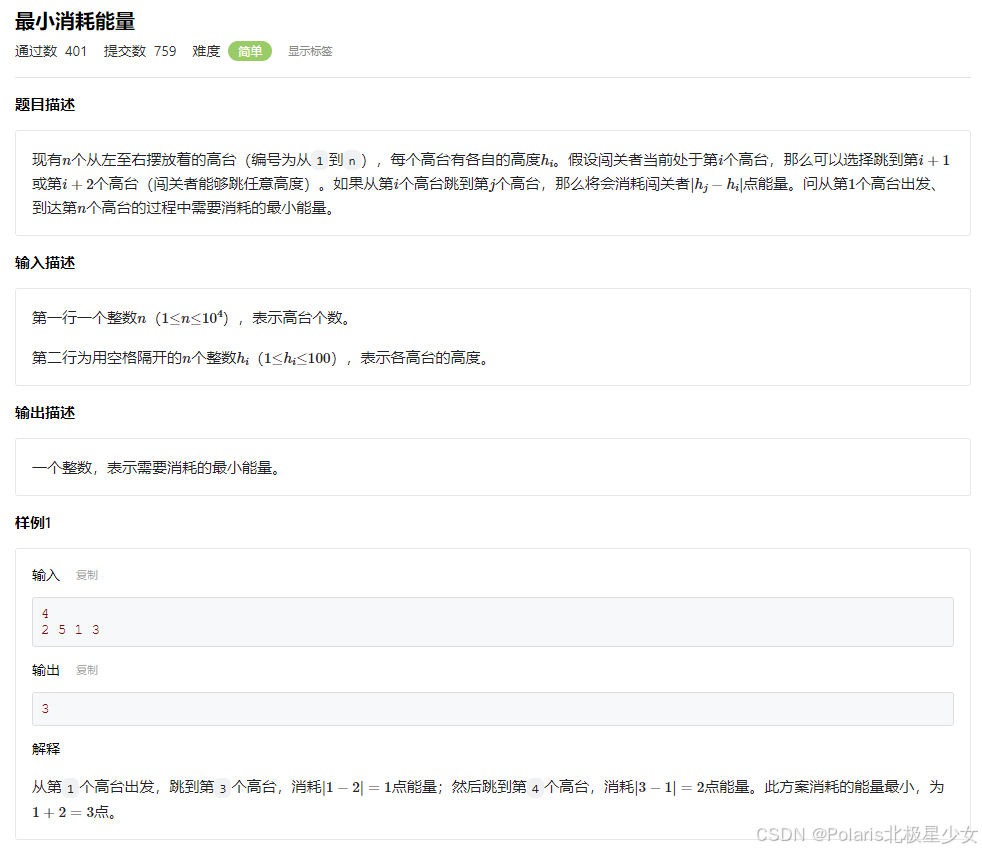
#include <cstdio> #include <algorithm> using namespace std;  const int MAXN = 10000; int h[MAXN]; int dp[MAXN];  int main() {     int n;     scanf("%d", &n);     for (int i = 0; i < n; i++) {         scanf("%d", &h[i]);     }     dp[0] = 0;     for (int i = 1; i < n; i++) {         dp[i] = dp[i - 1] + abs(h[i] - h[i - 1]);         if (i - 2 >= 0) {             dp[i] = min(dp[i], dp[i - 2] + abs(h[i] - h[i - 2]));         }     }     printf("%d", dp[n - 1]);     return 0; }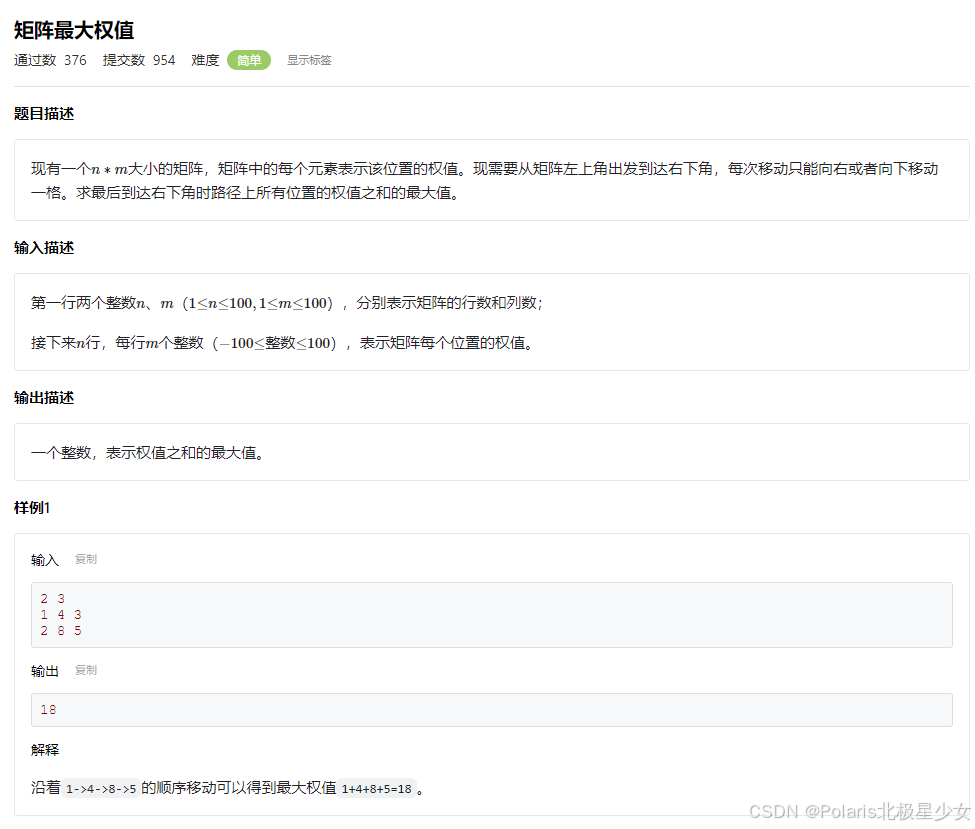

#include <cstdio> #include <algorithm> using namespace std;  const int MAXN = 100; int matrix[MAXN][MAXN]; int dp[MAXN][MAXN] = {0};  int main() {     int n, m;     scanf("%d%d", &n, &m);     for (int i = 0; i < n; i++) {         for (int j = 0; j < m; j++) {             scanf("%d", &matrix[i][j]);         }     }     // 初始化第一行和第一列的dp值     dp[0][0] = matrix[0][0];     for (int i = 1; i < n; i++) {         dp[i][0] = dp[i - 1][0] + matrix[i][0];     }     for (int j = 1; j < m; j++) {         dp[0][j] = dp[0][j - 1] + matrix[0][j];     }     // 状态转移方程     for (int i = 1; i < n; i++) {         for (int j = 1; j < m; j++) {             dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]) + matrix[i][j];         }     }     printf("%d", dp[n - 1][m - 1]);     return 0; }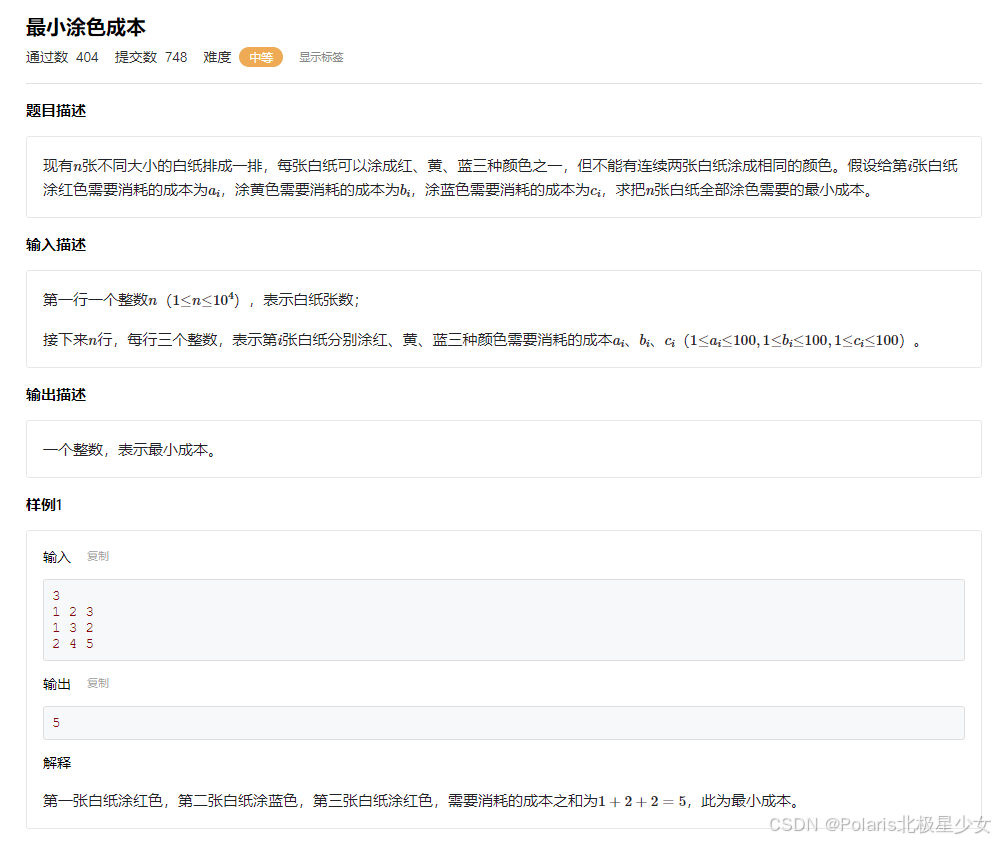

#include <cstdio> #include <algorithm> using namespace std;  const int MAXN = 10000; int a[MAXN], b[MAXN], c[MAXN]; int dp[MAXN][3];  int main() {     int n;     scanf("%d", &n);     for (int i = 0; i < n; i++) {         scanf("%d%d%d", &a[i], &b[i], &c[i]);     }     dp[0][0] = a[0];     dp[0][1] = b[0];     dp[0][2] = c[0];     for (int i = 1; i < n; i++) {         dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + a[i];         dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + b[i];         dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + c[i];     }     printf("%d", min(min(dp[n - 1][0], dp[n - 1][1]), dp[n - 1][2]));     return 0; }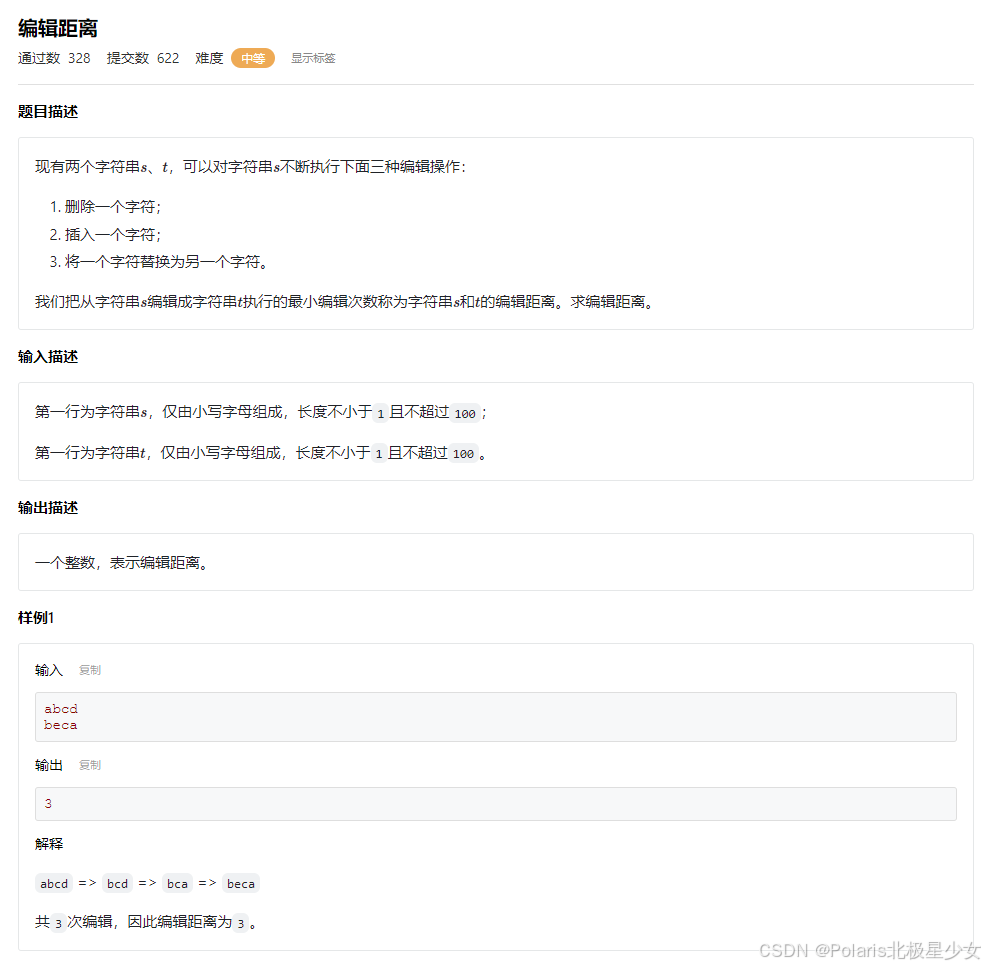

#include <iostream> #include <string> #include <algorithm> using namespace std;  const int MAXN = 100 + 1; int dp[MAXN][MAXN];  int main() {     string s, t;     cin >> s >> t;     for (int i = 0; i <= s.length(); i++) {         dp[i][0] = i;     }     for (int j = 0; j <= t.length(); j++) {         dp[0][j] = j;     }     for (int i = 1; i <= s.length(); i++) {         for (int j = 1; j <= t.length(); j++) {             dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);             dp[i][j] = min(dp[i][j], dp[i - 1][j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1));         }     }     cout << dp[s.length()][t.length()];     return 0; }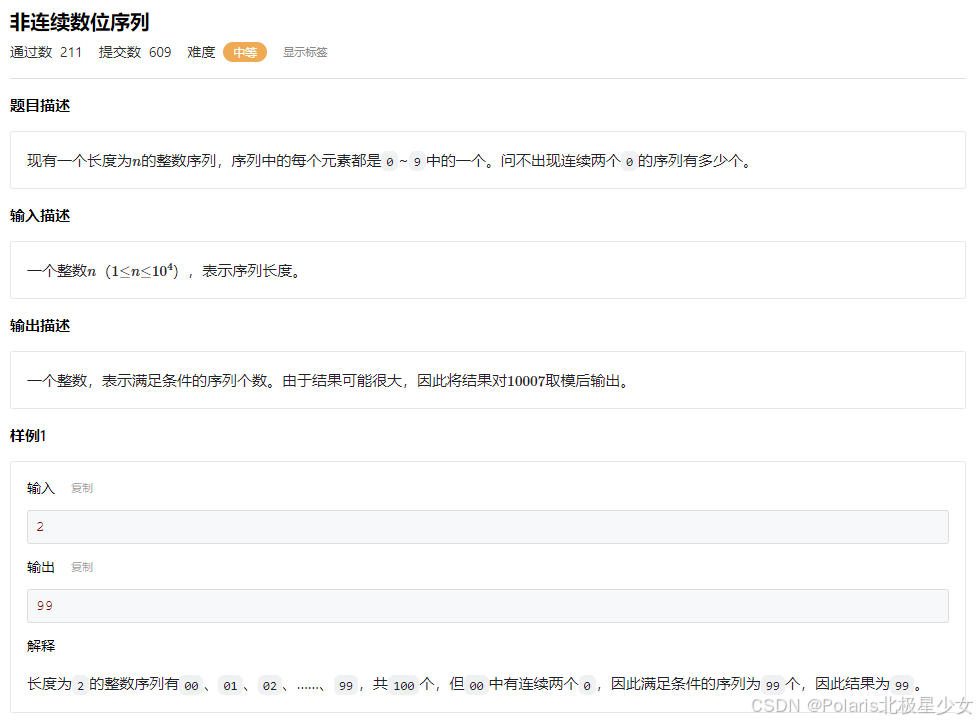

#include <iostream> #include <algorithm> #include <vector> using namespace std; const int mod =1e4+7; vector<int> dp(2,0),tmp(2,0); int n; //dp[0] 表示前一位选 0，dp[1]表示前一位不选0  int main(){      cin>>n;     dp[0]=1,dp[1]=9;     for(int i=2;i<=n;i++){         tmp[0] = dp[1];         tmp[1] = (dp[0]+dp[1])*9 % mod;         dp = tmp;     }     cout<<(dp[0]+dp[1])%mod<<endl;        return 0; }

相关阅读
  1. 如何查看和设置我的Android N设备的权限？
  2. 如何在安卓手机上自定义应用图标？
  3. 如何在安卓微信中同时听语音和查看图片？
  4. 华为哪些设备将支持升级至安卓7.0？
  5. 微信安卓软件中Q10功能有哪些独特之处？
  6. 安卓用户如何挑选最佳视频播放器应用？
  7. 安卓系统中用户文件目录的确切位置是什么？
  8. 小米4用户如何安全升级到安卓8.0系统？
  9. 如何成功将魅蓝5升级至安卓原生7.0版本？
  10. 16GB存储的安卓手机是否能满足日常需求？

广告一刻

为您即时展示最新活动产品广告消息，让您随时掌握产品活动新动态！