【Python实战因果推断】37_双重差分8_业界新闻

发布时间:2024-07-17 23:15

阅读量:4

您需要学习的 DID 的另一个变量是如何在模型中包含干预前协变量。这在您怀疑平行趋势不成立，但条件平行趋势成立的情况下非常有用：

$E\Big[Y(0)_{it = 1}-Y(0)_{it = 0}\Big|D=1,X\Big]=E\Big[Y(0)_{it = 1}-Y(0)_{it = 0}\Big|D=0,X\Big]$

考虑这种情况：您拥有与之前相同的营销数据，但现在您拥有全国多个地区的数据。如果你绘制出每个地区的干预结果和对照结果，你会发现一些有趣的现象：

 mkt_data_all = (pd.read_csv("./data/short_offline_mkt_all_regions.csv")  .astype({"date":"datetime64[ns]"}))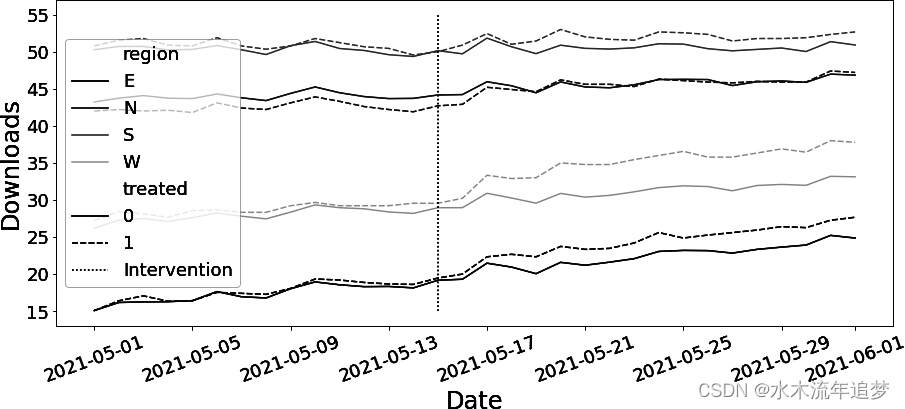

干预前的趋势在一个地区内似乎是平行的，但在不同地区之间却不是。因此，如果在这里简单地运行 DID 的双向固定效应规范，就会得到有偏差的 ATT 估计值：

 print("True ATT: ", mkt_data_all.query("treated*post==1")["tau"].mean())  m = smf.ols('downloads ~ treated:post + C(city) + C(date)',  data=mkt_data_all).fit()  print("Estimated ATT:", m.params["treated:post"])  True ATT: 1.7208921056102682  Estimated ATT: 2.068391984256296

您需要以某种方式考虑每个地区的不同趋势。您可能会认为，只需在回归中加入地区作为额外的协变量就能解决问题。但请再想一想！还记得使用单位固定效应如何消除任何时间固定协变量的影响吗？这不仅适用于不可观测的混杂因素，也适用于跨时间恒定的地区协变量。最终的结果是，天真地将其加入回归是无害的。您将得到与之前相同的结果：

 m = smf.ols('downloads ~ treated:post + C(city) + C(date) + C(region)',  data=mkt_data_all).fit()  m.params["treated:post"]    2.071153674125536

要想在 DID 模型中正确包含干预前协变量，您需要回顾一下 DID 的工作原理，即估算两个重要部分：干预基线和控制趋势。然后将控制趋势投射到治疗基线中。这意味着您必须分别估计每个地区的控制趋势。矫枉过正的做法是对每个地区分别进行差分回归。您可以在各个地区之间循环，或者将整个 DID 模型与地区虚拟变量进行交互：

 m_saturated = smf.ols('downloads ~ (post*treated)*C(region)',  data=mkt_data_all).fit() atts = m_saturated.params[  m_saturated.params.index.str.contains("post:treated")  ]atts  post:treated 1.676808 post:treated:C(region)[T.N] -0.343667 post:treated:C(region)[T.S] -0.985072 post:treated:C(region)[T.W] 1.369363 dtype: float64

请记住，ATT 估计值应根据基线组来解释，在本例中，基线组为东部地区。因此，对北部地区的影响为 1.67-0.34，对南部地区的影响为 1.67-0.98，以此类推。接下来，您可以使用加权平均法对不同的 ATT 进行汇总，其中一个地区的城市数量就是权重：

 reg_size = (mkt_data_all.groupby("region").size()  /len(mkt_data_all["date"].unique()))  base = atts[0]  np.array([reg_size[0]*base]+  [(att+base)*size  for att, size in zip(atts[1:], reg_size[1:])]  ).sum()/sum(reg_size)    1.6940400451471818

尽管我说这是矫枉过正，但这其实是个不错的主意。它很容易实现，也很难出错。不过，它也有一些问题。例如，如果你有很多协变量或连续协变量，这种方法就不切实际了。因此，我认为您应该知道还有另一种方法。与其将区域与治疗后和治疗后虚拟变量交互，您可以只与治疗后虚拟变量交互。这个模型将分别估计每个地区受治疗者的趋势（治疗前和治疗后的结果水平），但它将拟合一个截距移动到受治疗者和治疗后时期：

  m = smf.ols('downloads ~ post*(treated + C(region))',  data=mkt_data_all).fit()  m.summary().tables[1]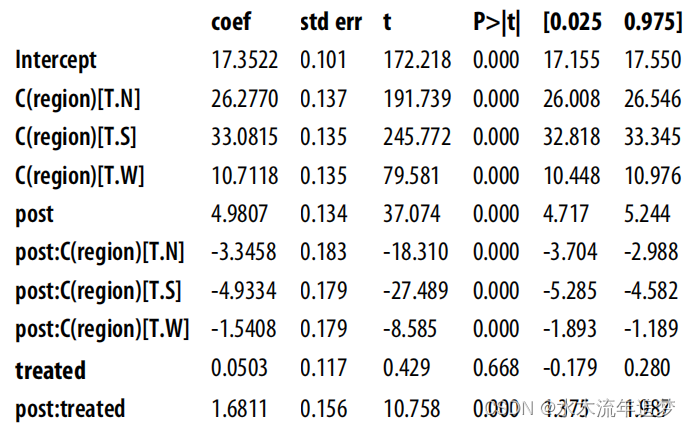

与 post:treated 相关的参数可以解释为 ATT。它与您之前得到的 ATT 并不完全相同，但非常接近。出现这种差异的原因是--您现在应该知道--回归按方差对各地区的 ATT 进行了平均，而之前是按地区大小进行平均的。这意味着回归会使干预分布更均匀（方差更大）的地区占更大比重。

第二种方法运行速度更快，但缺点是需要仔细考虑如何进行交互。因此，我建议您只有在真正了解自己在做什么的情况下才使用这种方法。或者，在使用之前，先尝试建立一些模拟数据，在这些数据中，您知道真实的 ATT，然后看看能否用您的模型恢复它。请记住：为每个地区运行一个 DID 模型并求取平均结果并不丢人。事实上，这是一个特别聪明的想法。