阅读量:1
目录
1. GJK算法
GJK算法是由Gilbert，Johnson，Keerthi 三位学者发明的，用来计算两个凸边形之间的碰撞检测，以及最近距离。
假设有空域形状水平投影构成的多边形A和空域形状水平投影多边形B，空域需求投影之间的水平距离距离d可以表示为：
同时引入闵可夫斯基(Minkowski)差集概念。
用多边形A的所有点减去多边形B中所有的点得到的一个点集合，可以用下式表示，示意图如下图所示：
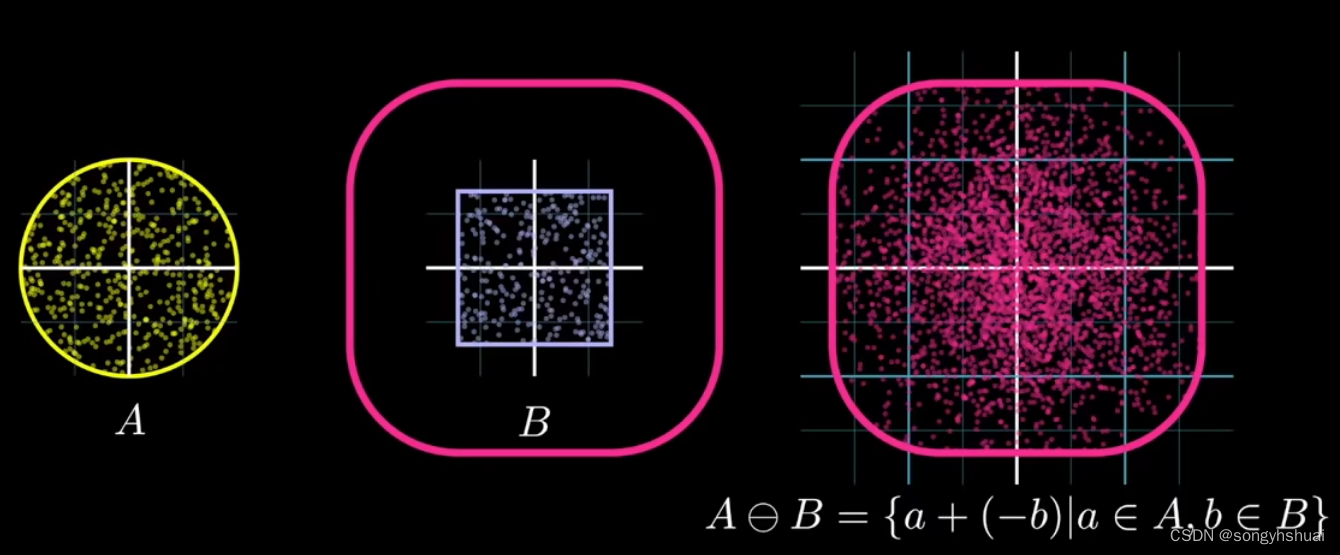
闵可夫斯基差集示意图
闵可夫斯基差集的意义在于可以获取两个多边形顶点间的坐标分布关系：若多边形A 与多边形B相交，那么差集中点会分布在原点四周，也就是说差集会包含原点。差集构成的多边形的形状与两个多边形之间的距离没有直接关系。两个多边形距离越大，则差集的中心位置离原点越远；反之，离原点越近。如果相交，则差集多边形会包含原点。
因此，GJK算法的结论是：如果两个空域形状存在重叠，那么这两个多边形构成的闵可夫斯基差集，必然会包含原点。判定两个形状的相交问题进一步的简化为，是否能够在多边形A、B的闵可夫斯基差中找到三个点以构成包含原点的三角形，这个三角形被称作是单行体。
2. 基于GJK算法的水平冲突检测模型
2.1 建立空间直角坐标系及还原空域本身形状
以用空需求水平范围1000×1000(km)为基础，建立直角坐标系。选定原点以后，取水平向右方向为x轴正方向，横坐标系范围由0至+1000；取竖直向上方向为y轴正方向，纵坐标系范围由0至+1000。由于申请位置集合一般用包含所申请空域的最小外接多边形的顶点表示，因此对于圆形空域和跑道型空域应根据其最小外接多边形还原其本身形状。
2.2 构建闵可夫斯基支撑点
根据多边形的特性，可以将方向映射到多边形上的点，而这个将方向向量映射到形状上的最远的点称为支撑点。选择两个空域需求多边形的中心连接起来的构成的向量，求取其支撑点；接着以该方向的反方向作为第二个多边形B上的方向，求取多边形形B上的支撑点。这两个点相减，就是闵可夫斯基差边界上的支撑点。
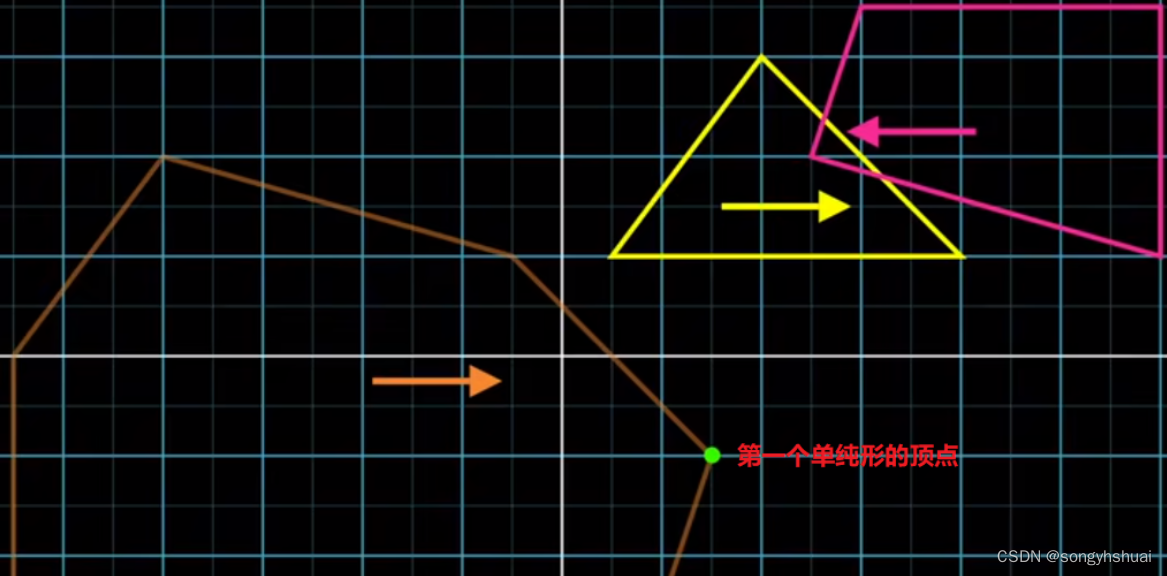
2.3 迭代寻找支撑点，构建三角形
以该支撑点为向量起点，找到指向原点的向量作为新的方向，并找到第二个支撑点。
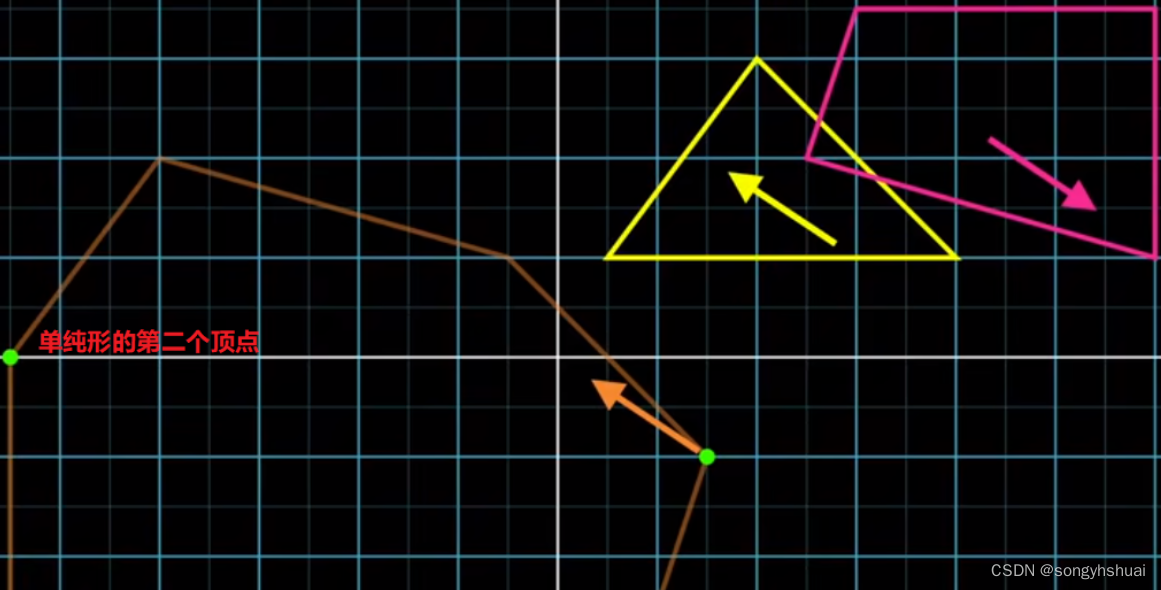我们现在可以做一个理智的判断，看看我们是否越过了原点。我们可以过原点，做垂直于方向D的一条线（二维情形），如果这条线可以把第一个加入单纯形的点和第二个加入单纯形的点分开到A和B两边，那么说明其可以跨越原点。如果不能分到A和B两边，说明其单纯形不可能包含原点，可以直接判断两个多边形不相交（提前终止条件）。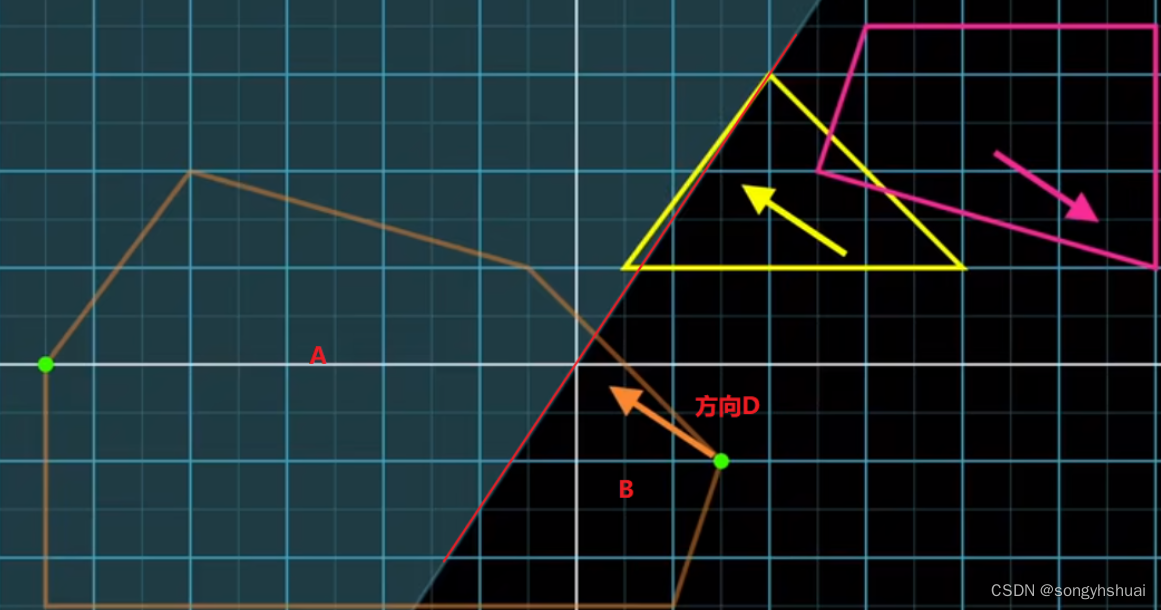
两个支撑点连成一条直线，垂直于该直线的向量，则为新的方向d并求出新的支撑点。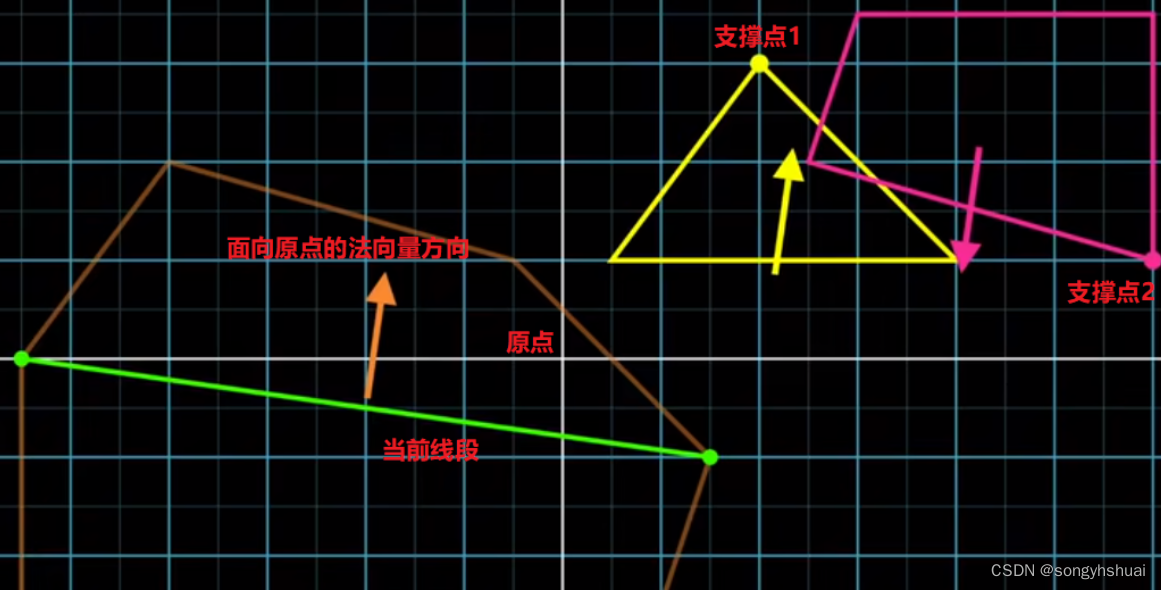
同样的我们做是否过原点判断。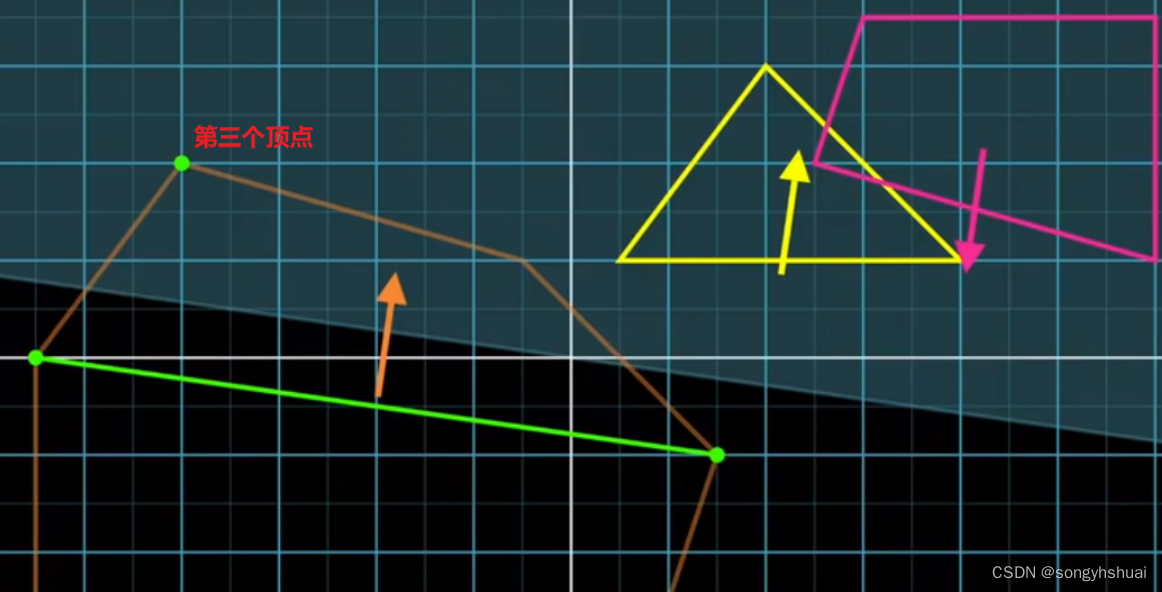
2.4 检查该三角形是否包含原点
根据三个支撑点连接构建三角形。若三角形内包含原点，则说明两个空域需求多边形相交，说明这两空域需求存在水平冲突；
如果三角形没有包含原点，则更新方向，添加新的支撑点。
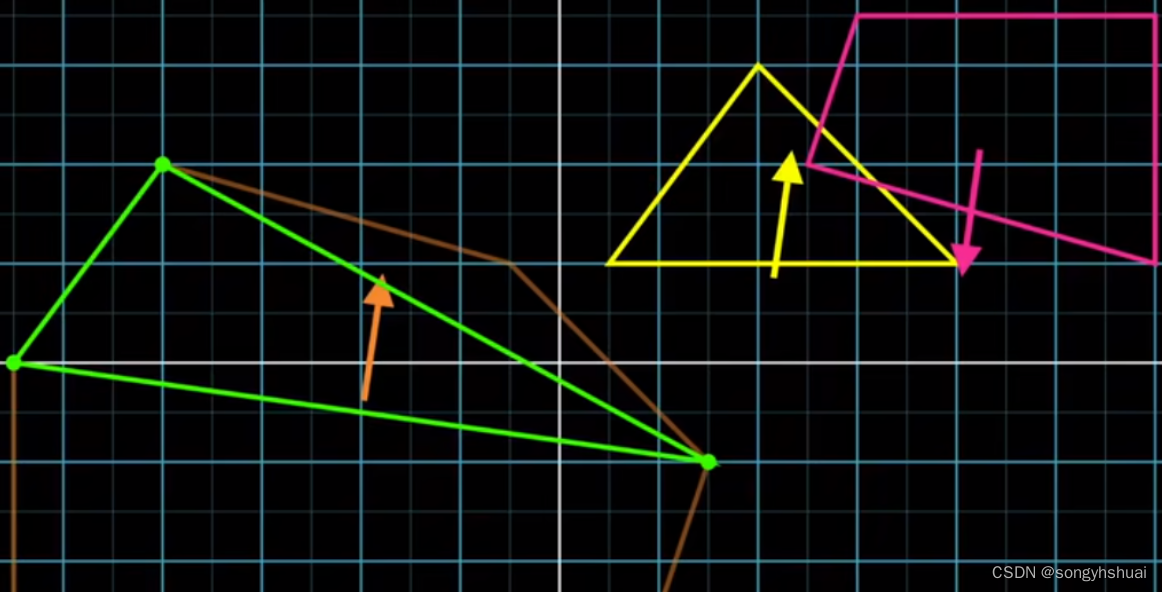选择其距离最接近原点的三角形边的垂直向量并保留这条边上的两个点，删除剩余的一个点，并将该垂直向量作为新的方向再次寻找第三个支撑点，做下一次迭代并判断新的三角形是否包含原点。
如果迭代后新的三角形和原来的三角形是同一个，则说明不存在包含原点的三角形，此时退出迭代循环。
2.5 求解空域形状间最小距离
如果最后三角形不包含原点，此时可以求取空域两个形状间的最小距离。利用点到直线之间的距离公式，可求出原点到最接近原点的边的距离，该距离为两个空域需求多边形之间的最小距离，即两个空域需求水平间隔。
2.6 判断是否存在水平冲突
空域需求之间两两逐对计算空域间的闵可夫斯基差集，判断其与原点的包含关系，检测两两空域间是否存在冲突。若求得三角形图像不包含原点，则判断两个空域需求水平间隔是否小于最小水平安全间隔，若小于最小安全间隔则认为两空域需求之间存在水平冲突，进一步地可以判断出两空域需求间存在空域冲突。
3. GJK算法的matlab实现
3.1 主函数部分
输入的数列shap_1 和 shap_2 涉及到不同的图像，有圆形、多边形和跑道形状。数列的第一项为标识项，1为圆、2为四边形、3为五边形、4为六边形、5为跑道形状。圆的第二三项没有数据，第四五项为圆心坐标（x，y），第六项为半径。其余的图像，第二三项表示各个图象的几何中心，后面的依次为各个图像的顶点坐标（x，y）。其中跑道形状有其外接矩形顶点表示。
输出的out表示不同的情况，1表示迭代过程中，未通过过原点检测，退出迭代；2表示形成的三角形可以包围原点；3表示迭代形成的三角形前后重复。
mindiastance为最小距离
ci表示循环迭代的次数
function [out,mindistance,ci] = GJK(shap_1,shap_2) % 初始化单纯形 out = 0; simple = []; origin = [0,0]; % 原点 n = 1; % 记录迭代次数 % 第一次迭代 direction = getInitDirection(shap_1,shap_2); % 获取初始方向 vertex = getNewVertex(shap_1,shap_2,direction); % 根据给定的方向和多边形，获取单纯形新顶点 simple(n,1:2) = vertex; % 第二次迭代 n = n + 1; direction = diff_1(origin,vertex); vertex = getNewVertex(shap_1,shap_2,direction); % 过原点检查 if isCrossingOriginVector(diff_1([0 0],simple(1,1:2)),vertex) == 1 out = 1; % 此时可以证明无法发生碰撞 end simple(n,1:2) = vertex; n = n+1; % 第三次迭代 direction = getLineFaceToOriginVector(simple(1,1:2),simple(2,1:2)); direction = direction vertex = getNewVertex(shap_1,shap_2,direction); % 过原点检查 if isCrossingOriginVector(direction,vertex) == 1 out = 1; % 此时可以证明无法发生碰撞 n1 = 1 end % if isCrossingOriginVector(simple(2,1:2),vertex) == 0 % out = 1; % 此时可以证明已经过原点，可以证明会发生碰撞,并且是边缘碰撞 % end simple(n,1:2) = vertex; n = n+1; ci = 0; % disp(simple); if out == 0 % 开始循环 for i = 1:10000 % 判断当前的单纯形体的三个顶点构成的三角形是否包含原点 if isContainOrigin(simple(1,1:2),simple(2,1:2),simple(3,1:2)) == 1 out = 2; % 此时可以证明已经过原点，可以证明会发生碰撞,并且是绝对碰撞 break; end % 找到三角形距离原点最近的边 minIndex1 = -1; minIndex2 = -1; for x = 1:length(simple)-1 for y = x+1:length(simple) distance = calcPointToLineDistance([0 0],simple(x,1:2),simple(y,1:2)); if minIndex1 == -1 || distance < minDistance minDistance = distance; minIndex1 = x; minIndex2 = y; end end end % 找方向 direction = getLineFaceToOriginVector(simple(minIndex1,1:2),simple(minIndex2,1:2)); vertex = getNewVertex(shap_1,shap_2,direction); % 是否存在当前单纯形检查 for z = 1: length(simple) if isEquals(simple(z,1:2),vertex) == 1 out = 3; end end if out == 3 break; % 如果未通过单纯形体检查则跳出该循坏 end % 过原点检查 if isCrossingOriginVector(direction,vertex) == 1 out = 1; % 此时可以证明未通过过原点检测 % 更新单纯形 vertex1 = simple(minIndex1,1:2); vertex2 = simple(minIndex2,1:2); simple(1,1:2) = vertex1; simple(2,1:2) = vertex2; simple(3,1:2) = vertex; break; end % 更新单纯形 vertex1 = simple(minIndex1,1:2); vertex2 = simple(minIndex2,1:2); simple(1,1:2) = vertex1; simple(2,1:2) = vertex2; simple(3,1:2) = vertex; end ci = i; end % 找到三角形距离原点最近的边 mindistance = 0; minIndex1 = -1; for x = 1:length(simple)-1 for y = x+1:length(simple) distance = calcPointToLineDistance([0 0],simple(x,1:2),simple(y,1:2)); if minIndex1 == -1 || distance < mindistance mindistance = distance; minIndex1 = x; end end end disp(simple); end 3.2 获取初始方向
获取初始两个几何形状之间的方向，有两个几何图形中心相减。
function [out] = getInitDirection(shap_1,shap_2) if(shap_1(1) == 1 ) out_1(1:2) = shap_1(4:5); else out_1(1:2) = shap_1(2:3); end if(shap_2(1) == 1 ) out_2(1:2) = shap_2(4:5); else out_2(1:2) = shap_2(2:3); end out = out_1 - out_2; end3.3 根据给定的方向和多边形，获取单纯形新顶点
% 根据给定的方向和多边形，获取单纯形新顶点 % 先把跑道轨迹看成矩形 function [out] = getNewVertex(shap_1,shap_2,direction) if shap_1(1) == 1 supportPoint1 = supportCircle(shap_1,direction); elseif shap_1(1) == 5 supportPoint1 = supportP(shap_1,direction); else supportPoint1 = support(shap_1,direction); end if shap_2(1) == 1 supportPoint2 = supportCircle(shap_2,-direction); elseif shap_2(1) == 5 supportPoint2 = supportP(shap_2,-direction); else supportPoint2 = support(shap_2,-direction); end supportPoint1 = supportPoint1 supportPoint2 = supportPoint2 out = diff_1(supportPoint1,supportPoint2); end 若图形为圆
% Support 函数(圆形) function [out] = supportCircle(shap,direction) theta = calc2DVectorsAngle(direction,[1,0]); if(direction(2)<0) theta = 2*pi - theta; end out = [shap(4)+shap(6)*cos(theta),shap(5)+shap(6)*sin(theta)]; end% 计算两个二维向量的夹角[0,PI] function [out] = calc2DVectorsAngle(direction,shap) d1 = norm(direction,2); d2 = norm(shap,2); out = acos((direction(1)*shap(1)+direction(2)*shap(2))/(d1*d2)); end若图形为多边形
% support 函数（常规多边形） function [out] = support(shap,direction) maxIndex = 0; maxDot = dot_1([shap(4),shap(5)],direction); if shap(1) == 2 || shap(1) == 5 n = 4; elseif shap(1) == 3 n = 5; elseif shap(1) == 4 n = 6; end for i = 1:n-1 d = dot_1([shap(4+2*i),shap(5+2*i)],direction); if d > maxDot maxDot = d; maxIndex = 2*i; end end out = [shap(4+maxIndex),shap(5+maxIndex)]; % 输出多边形和给定方向的顶点 end %两维向量点乘 function [out] = dot_1(v1,v2) out = v1(1)*v2(1)+v1(2)*v2(2); end若图像为跑道
% 跑道图形 function [out] = supportP(shap,direction) r = (shap(11)-shap(9))/2; low = shap(8)+r;high = shap(4)-r; % shap_1 = [0 0 0 high shap(5) high shap(7) low shap(7) low shap(5)]; % row = diff_1([low shap(9)+r],[shap(2) shap(3)]); % row_1 = diff_1([high shap(9)+r],[shap(2) shap(3)]); if direction(1) <= 0 out = supportCircle([1,0,0,low,shap(9)+r,r],direction); else out = supportCircle([1,0,0,high shap(9)+r,r],direction); end end % 二维向量相减 function [out] = diff_1(shap_1,shap_2) out = shap_1 - shap_2; end 3.4 过原点检测函数
% 过原点检查 function [out] = isCrossingOriginVector(v1,v2) if dot_1(v1,v2)>=0 out = 0; else out = 1; end end 3.5 根据两个支撑点求取方向
% 传入两个点，获取它构成的边面向原点的法向量 function [out] = getLineFaceToOriginVector(A,B) if A(1) == B(1) if A(1) >= 0 out = [-1 0]; else out = [1 0]; end elseif A(2) == B(2) if A(2) >= 0 out = [0 -1]; else out = [0 1]; end else k = (A(2) - B(2))/(A(1) - B(1)); k1 = -1/k; b = A(2) - k*A(1); x = -k*b/(k*k+1); y = k1*x; out = diff_1([0 0],[x y]); end end 3.6 判断三角形是否包含原点
% 传入三个点，判断由三个点组成的三角形是否包含原点 function [out] = isContainOrigin(p1,p2,p3) origin = [0 0]; a = calcTriangleArea(origin,p1,p2); b = calcTriangleArea(origin,p1,p3); c = calcTriangleArea(origin,p2,p3); s = calcTriangleArea(p3,p1,p2); if abs(a+b+c-s) <0.00001 out = 1; % 证明原点在三角形内 else out = 0; % 证明原点不在三角形内 end end% 传入三个点，根据海伦公式计算三角形的面积 function [out] = calcTriangleArea(p1,p2,p3) a = calcPointToPointDistance(p1,p2); b = calcPointToPointDistance(p1,p3); c = calcPointToPointDistance(p2,p3); p = (a+b+c)/2; out = sqrt(p*(p-a)*(p-b)*(p-c)); end% 计算两个点的距离 function [out] = calcPointToPointDistance(p1,p2) out = sqrt((p1(1)-p2(1))^2+(p1(2)-p2(2))^2); end3.7 求取原点到边的距离
% 求取原点到一条边的距离 function [out] = calcPointToLineDistance(p0,p1,p2) out2 = norm(p1,2); out3 = norm(p2,2); if p2(1) - p1(1) == 0 out = abs(p2(1)); else a = (p2(2)-p1(2))/(p2(1)-p1(1)); b = -1; c = p1(2)-a*p1(1); out1 = abs(a*p0(1)+b*p0(2)+c)/sqrt(a*a+b*b); x = (-1*a*c)/(a*a+1); if (x >= p1(1) && x <= p2(1)) || (x >= p2(1) && x <= p1(1)) out = out1; elseif out2 <= out3 out = out2; else out = out3; end end end 3.8 判断前后迭代形成的新的支撑点是否重复
% 判断两维向量是否相等 function [out] = isEquals(p1,p2) if abs(p1(1) - p2(1)) == 0 && abs(p1(2) - p2(2)) == 0 out = 1; else out = 0; end end