【计算几何】凸多面体重叠判断算法：GJK 算法详解 & C++代码实现二维情形的凸多边形重叠判断

avatar
作者
筋斗云
  • 首页»
  • 业界新闻»
  • 新闻资讯»
  • 【计算几何】凸多面体重叠判断算法：GJK 算法详解 & C++代码实现二维情形的凸多边形重叠判断
阅读量:1

文章目录

一、GJK 算法简介

GJK 算法是由 Gilbert，Johnson，Keerthi 三位前辈发明的，用来计算两个凸多面体之间的碰撞检测，以及最近距离。

GJK 算法可以在 O ( M + N ) O(M+N) O(M+N) 的时间复杂度内，检测出碰撞，算法在每次迭代的过程中，都会优先选择靠近原点的方向，因此收敛速度会很快。算法的证明过程比较复杂，但是原理还是比较容易理解的。

GJK的初衷是确定两个凸包之间的距离。GJK还可以用于在小距离穿透情况下获取碰撞信息，并可以通过其他算法进行补充以实现更大距离的穿透。

二、前置知识

2.1 二维向量的点乘和叉乘

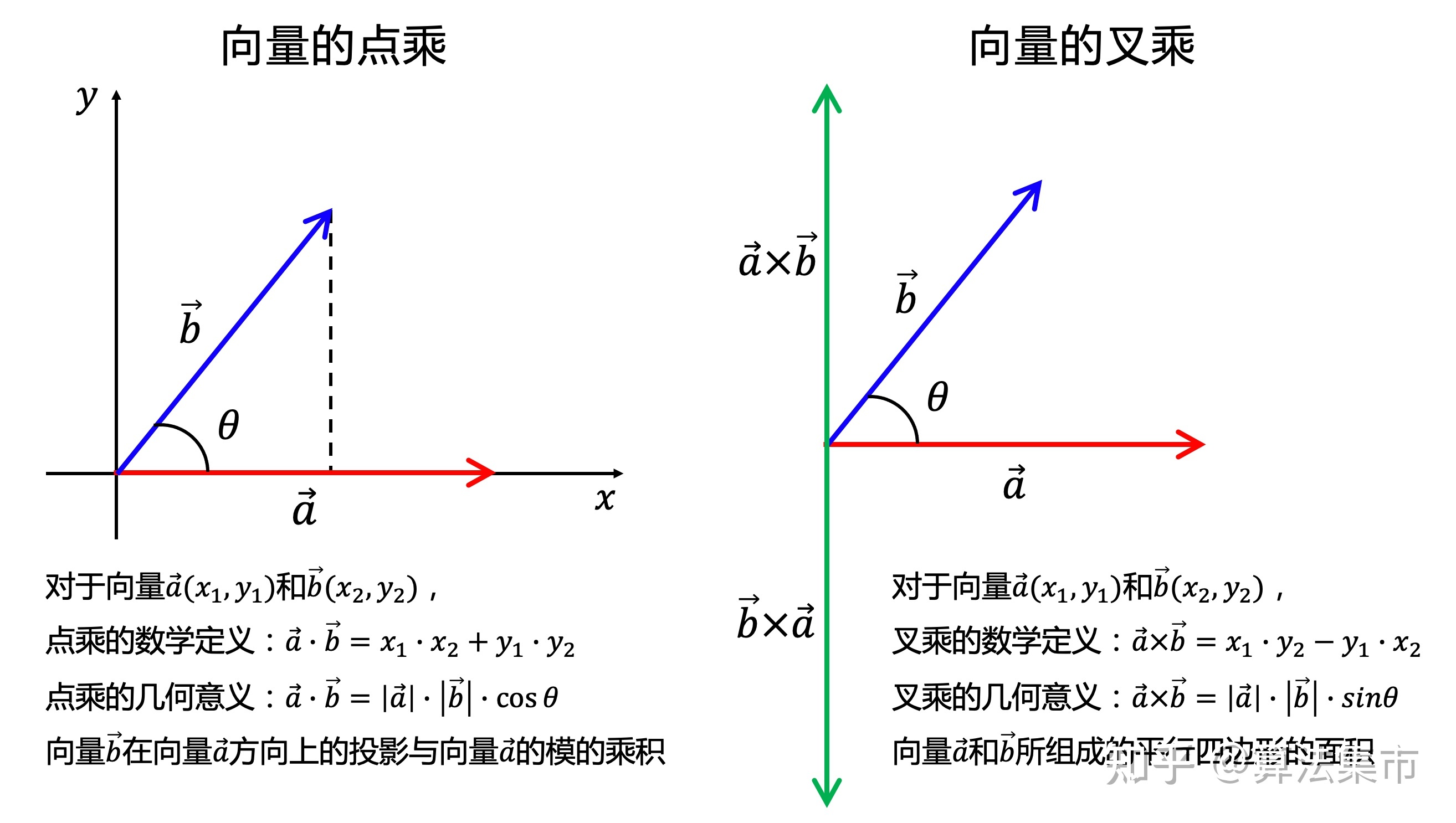
下图来自知乎：算法集市

  • 向量的点乘用来判断两个向量是否同方向
  • 向量的叉乘用来判断一点在一线段的左侧还是右侧

在这里插入图片描述

下面是C++代码实现的向量点乘和叉乘（二维情形）

/* 二维向量叉乘 */ double product(double* v1,double* v2){ 	return v1[0] * v2[1] - v1[1] * v2[0]; }  /* 二维向量点乘 */ double dot(double* v1, double* v2){ 	return v1[0] * v2[0] + v1[1] * v2[1]; }

2.2 三维向量叉乘

下图来自 向量的内积与外积
在这里插入图片描述

C++代码实现：

/* 三维向量叉乘 */ double* product3D(double* v1, double* v2){ 	return new double[]{v1[1] * v2[2] - v2[1] * v1[2],-(v1[0] * v2[2] - v2[0] * v1[2]),v1[0] * v2[1] - v2[0] * v1[1]}; }

2.3 凸多边形

凸多边形是一个内部为凸集的简单多边形。凸多边形（Convex Polygon）指如果把一个多边形的所有边中，任意一条边向两方无限延长成为一直线时，其他各边都在此直线的同旁，那么这个多边形就叫做凸多边形，其内角全不是优角，任意两个顶点间的线段位于多边形的内部或边上。

优角(reflex angle)亦称凹角，指大于平角(180°)而小于周角(360°)的角。直角、锐角和钝角统称劣角。

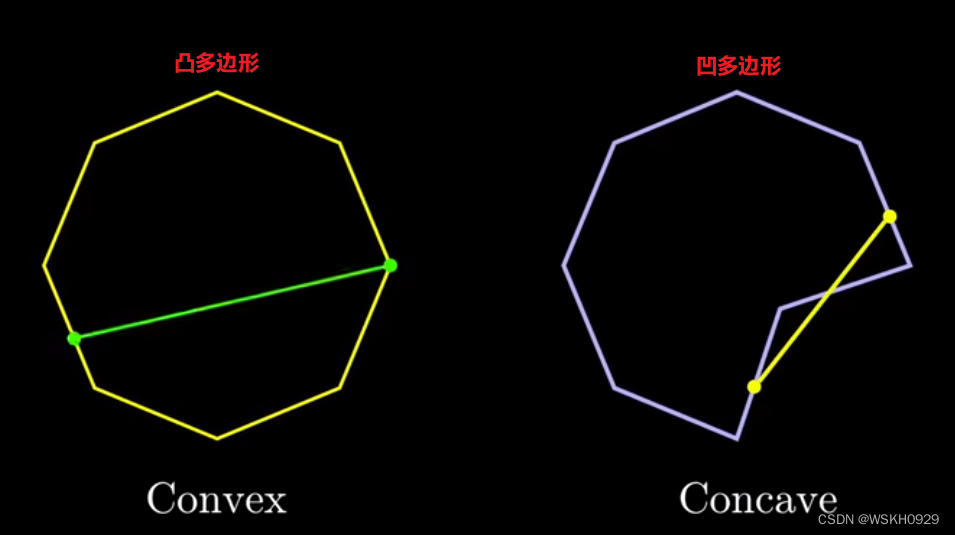
在这里插入图片描述
在程序中，我们可以利用向量的叉乘来判断一个多边形是否为凸多边形：

  • 若多边形的顶点是逆时针序列，则向量的叉乘 a x b，b x c，c x d，d x e，e x a 的结果均大于0（abcde代表多边形的5个顶点，这里只是举例，实际不一定是5个）
  • 若多边形的顶点是顺时针序列，则向量叉乘的结果均小于0
  • 但若同时存在大于0 和 小于0 的结果，则说明是凹多边形

下面是判断多边形是否为凸多边形的C++代码实现（二维情形）

/* 判断一个多边形是否为凸多边形 */ bool isConvex(vector<double*> poly){ 	// 判断多边形是否为顺时针 	bool clockwise = product(new double[]{poly[1][0] - poly[0][0], poly[1][1] - poly[0][1]}, new double[]{-1, 0}) >= 0; 	for (int i = 0; i < poly.size(); i++){ 		double d = i + 1 < poly.size() ? product(poly[i], poly[i + 1]) : product(poly[i], poly[0]); 		if ((clockwise && d > 0) || (!clockwise && d < 0)){ 			return false; 		} 	} 	return true; }

2.4 闵可夫斯基差

闵可夫斯基差，也可以叫做闵可夫斯基和，它的定义也很好理解，点集A与B的闵可夫斯基和被定义为：

A + B = { a + b ∣ a ∈ A ， b ∈ B } A + B = \{a + b | a ∈ A，b ∈ B\} A+B={a+b∣a∈A，b∈B}

定理：如果 A 和 B 是两个凸多边形，则 A + B 也是凸多边形。

闵可夫斯基和从几何上的直观理解是A集合沿B的边际连续运动一周扫过的区域与B集合本身的并集，也可以是B沿着A的边界连续运动扫过区域与A自身的并集。

GJK算法用到的不是闵可夫斯基和，而是闵可夫斯基差，即：

A − B = { a − b ∣ a ∈ A ， b ∈ B } A - B = \{a - b | a ∈ A，b ∈ B\} A−B={a−b∣a∈A，b∈B}

虽然使用的是减法运算，但其仍然是闵可夫斯基和，相当于先对B中的所有点做负运算（相对原点的镜像），然后再与A做加法

运用：GJK算法的核心就是闵可夫斯基差，即若两个多边形相交，则它们的闵可夫斯基差必然包括原点

下面来看两个例子：

第一个例子：下图展示了多边形A和B相交的情况，他们的闵可夫斯基差包含原点

在这里插入图片描述
第二个例子：下图展示了多边形A和B不相交的情况，他们的闵可夫斯基差没有包含原点

在这里插入图片描述

2.5 单纯形

k 阶单纯形（simplex），指的是k维空间中的多胞形，该多胞形是 k+1 个顶点组成的凸包。

在 GJK 算法中，单纯形被大量使用。单纯形指的是点、线段、三角形或四面体。例如，0阶单纯形是点，1阶单纯形是线段，2阶单纯形是三角形，3阶单纯形是四面体。

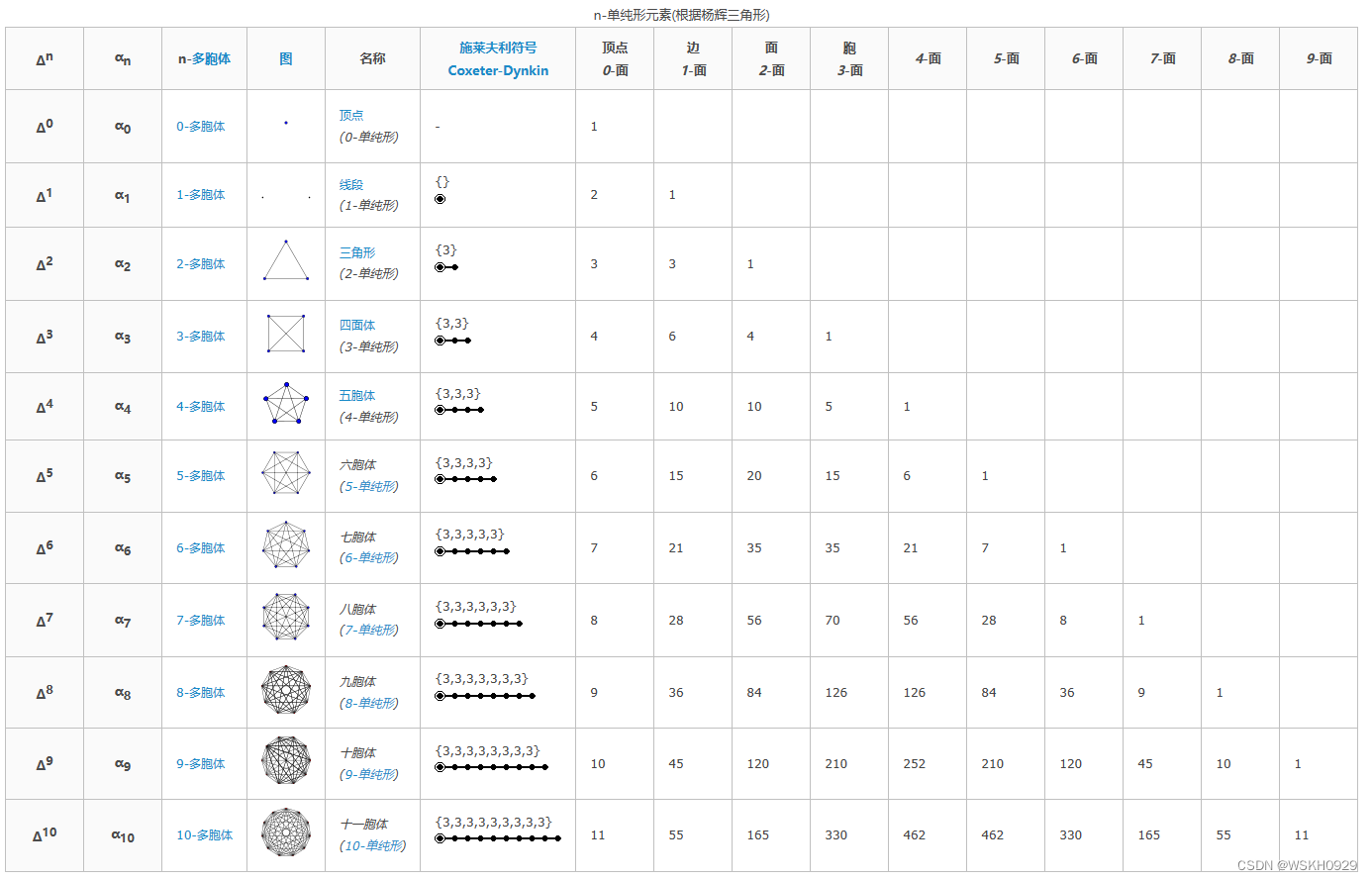
在这里插入图片描述

对于二维空间的多边形，最多用到2阶单纯形。那单纯形到底有什么作用呢？

对于上面两个相交的多边形例子，实际应用中，其实不需要求出完整的闵可夫斯基差，只需要在闵可夫斯基差内形成一个多边形，如下图所示，并使这个多边形尽可能包围原点，这个多边形就称为单纯形。即假如单纯形包围原点，则闵可夫斯基差必然包围原点。

2.6 Support 函数

Support 函数的作用是计算多边形在给定方向上的最远点。

如下图所示，在向量 d 方向的最远点为 v0 点。这里在寻找给定方向上的最远点时，需要用到向量的点乘。我们可以遍历每个顶点和向量d的点乘，找到点乘值最大的顶点，它就是向量 d 方向的最远点。这个点也被称为支撑点。

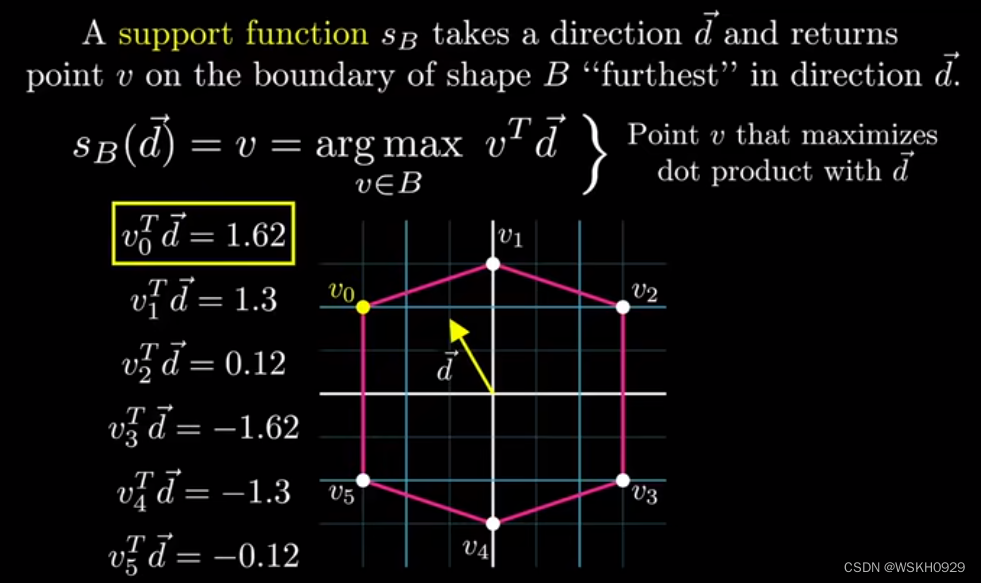
在这里插入图片描述

为什么需要Support函数呢？这是因为在构建单纯形时，我们希望尽可能得到闵可夫斯基差的顶点，而不是其内部的一个点，这样产生的单纯形才能包含最大的区域，增加算法的快速收敛性。

值得一提的是，针对一些特殊的多边形，例如：圆、椭圆等，我们可以利用其参数方程，很容易的得到其方向 d 上的最远顶点。

在这里插入图片描述
在这里插入图片描述

下面是C++代码实现常规多边形、圆形和椭圆形的 Support 函数

/* Support 函数（常规多边形） */ double* support(vector<double*> poly, double* direction){ 	int maxIndex = 0; 	double maxDot = dot(new double[]{poly[0][0], poly[0][1]}, direction); 	for (int i = 1; i < poly.size(); i++){ 		double d = dot(new double[]{poly[i][0], poly[i][1]}, direction); 		if (d > maxDot){ 			maxDot = d; 			maxIndex = i; 		} 	} 	return new double[]{poly[maxIndex][0], poly[maxIndex][1]}; }  /* 计算两个二维向量的夹角（度）[0,PI] */ double calc2DVectorsAngle(double* v1, double* v2){ 	double d1 = sqrt(pow(v1[0] - 0, 2) + pow(v1[1] - 0, 2)); 	double d2 = sqrt(pow(v2[0] - 0, 2) + pow(v2[1] - 0, 2)); 	// 获取弧度夹角 [0,PI] 	return acos((v1[0] * v2[0] + v1[1] * v2[1]) / (d1*d2)); }  /* Support 函数（圆形） */ double* supportCircle(double* centerPoint,double r, double* direction){ 	// 获取theta 	double theta = calc2DVectorsAngle(direction, new double[]{1, 0}); 	if (direction[1] < 0){ 		theta = 2 * PI - theta; 	} 	// 根据圆的参数方程返回支撑点 	return new double[]{centerPoint[0] + r * cos(theta), centerPoint[1] + r * sin(theta)}; }  /* Support 函数（椭圆形） */ double* supportEillpse(double* centerPoint, double a,double b, double* direction){ 	// 获取theta 	double theta = calc2DVectorsAngle(direction, new double[]{1, 0}); 	if (direction[1] < 0){ 		theta = 2 * PI - theta; 	} 	// 根据椭圆的参数方程返回支撑点 	return new double[]{centerPoint[0] + a * cos(theta), centerPoint[1] + b * sin(theta)}; }

综上所述，只要需要进行重叠判断的两个多边形都可以被Support，且都为凸多边形，那么就可以采用GJK算法进行求解

三、GJK 算法讲解

有了上述前置知识，接下来就可以开始讲解 GJK 算法了

首先我们要明确的，GJK 的核心逻辑是：给定两个多边形 A 和 B，以及一个初始方向，通过迭代的方式构建、更新单纯形，并判断单纯形是否包含原点，若包含原点则两个多边形相交，否则不相交。

3.1 熟悉 GJK 算法流程

下面让我们用两个例子，熟悉一下GJK 算法的流程

3.1.1 多边形重叠的情形

首先，我们可以通过随机的方式，得到一个初始方向，然后，其中一个多边形用初始方向找支撑点，另一个多边形则用初始方向的反方向找支撑点。这样就得到了两个支撑点

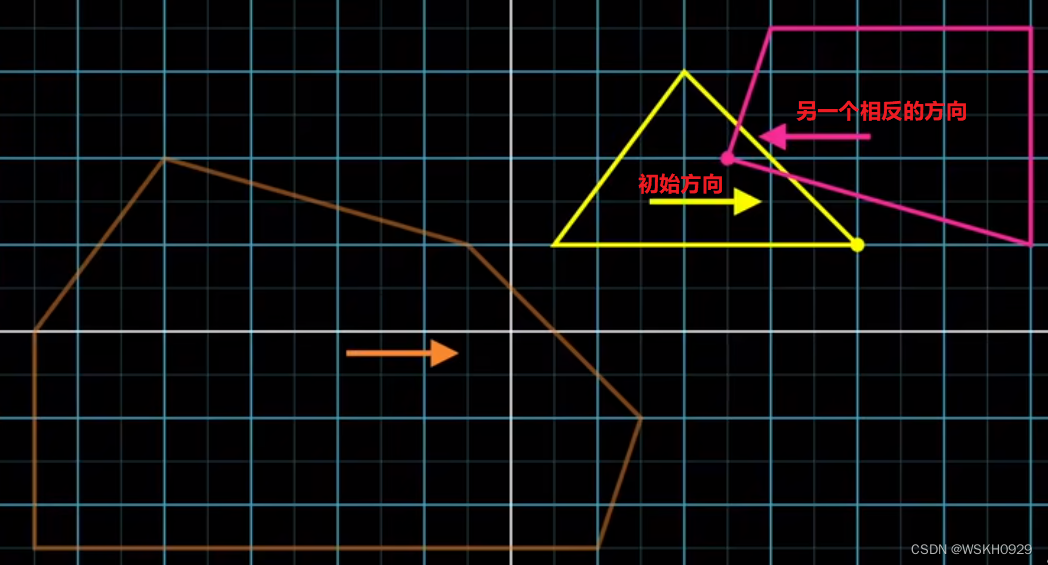
在这里插入图片描述

然后根据找到的两个支撑点，做闵可夫斯基差，得到第一个单纯形的顶点

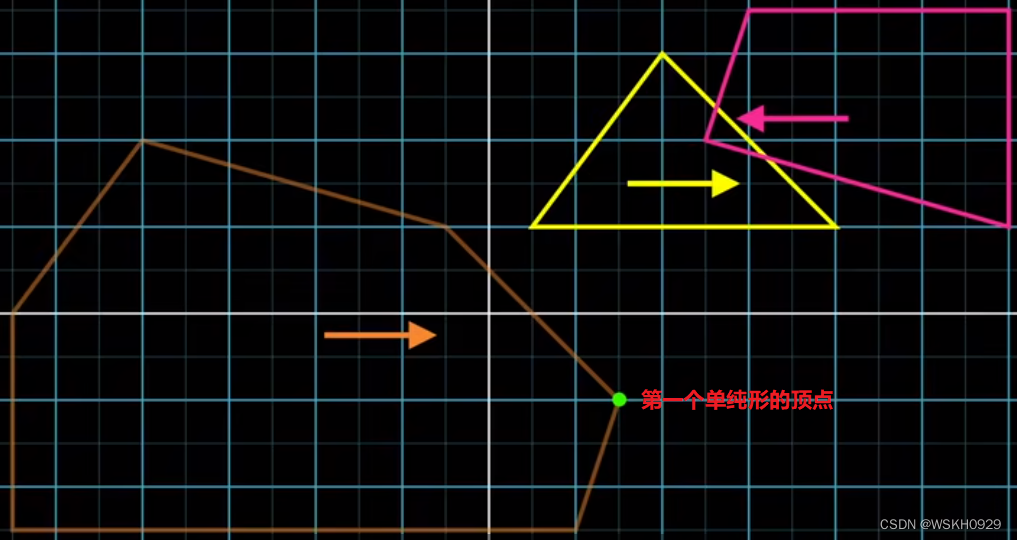
在这里插入图片描述

根据经验，我们知道下一个最有探索意义的方向是第一个单纯形顶点朝向原点的方向，如下图所示。同样，方向确定，我们可以通过 Support 函数分别得到两个多边形在该方向上的支撑点

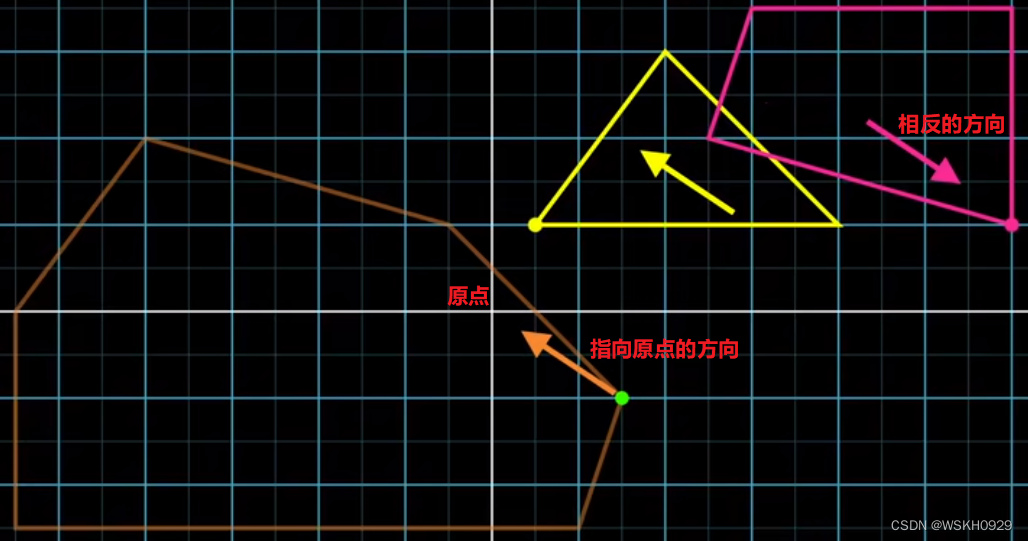
在这里插入图片描述

然后，再根据得到的两个支撑点做闵可夫斯基差，得到单纯形的第二个顶点，如下图所示

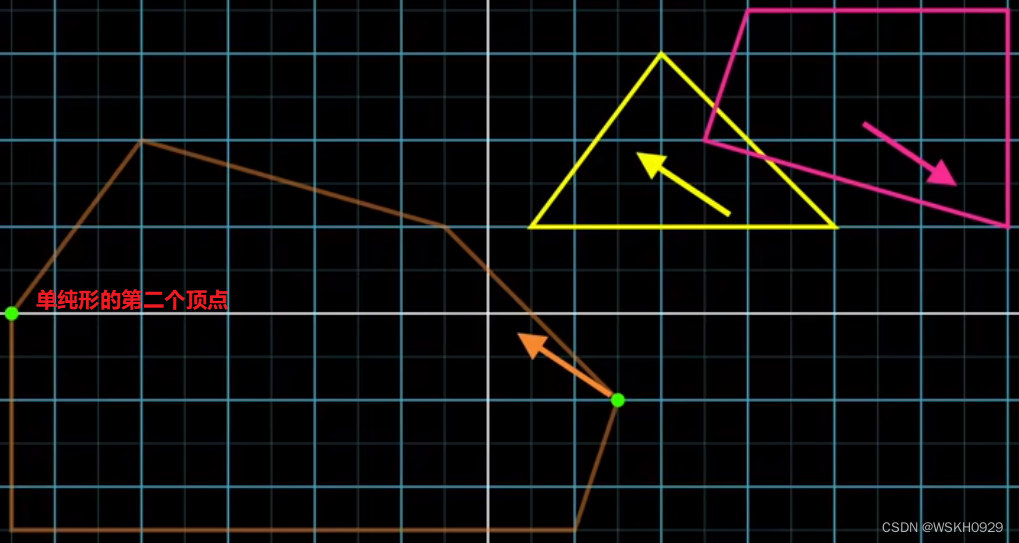
在这里插入图片描述

我们现在可以做一个理智的判断，看看我们是否越过了原点。我们可以过原点，做垂直于方向D的一条线（二维情形），如果这条线可以把第一个加入单纯形的点和第二个加入单纯形的点分开到A和B两边，那么说明其可以跨越原点。如果不能分到A和B两边，说明其单纯形不可能包含原点，可以直接判断两个多边形不相交（提前终止条件）。

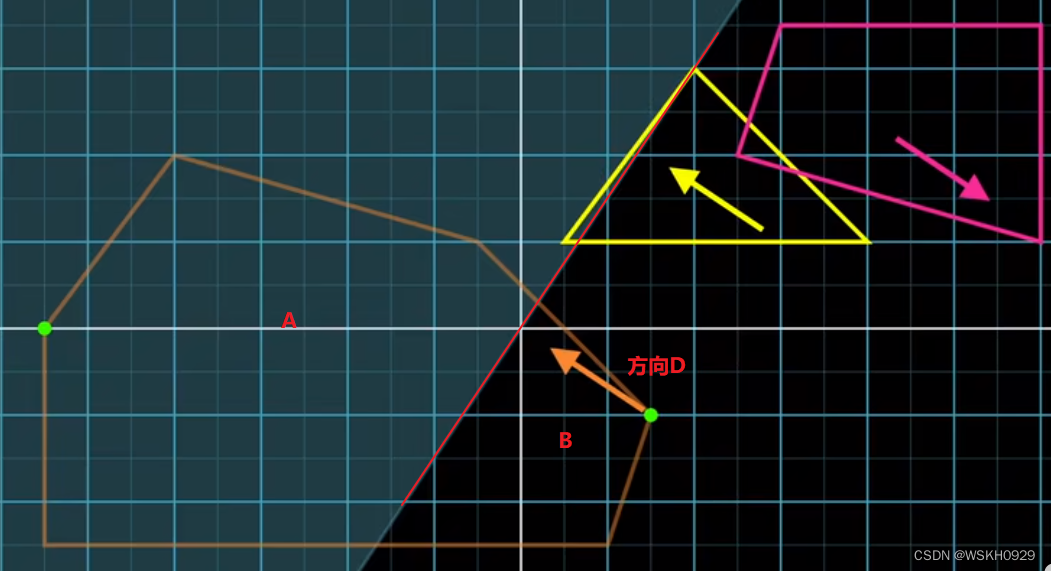
在这里插入图片描述
我们现在需要选择下一个方向，GJK 选择的方向是当前线段面向原点的法向量方向。然后我们可以根据这个方向分别得到两个多边形的支撑点

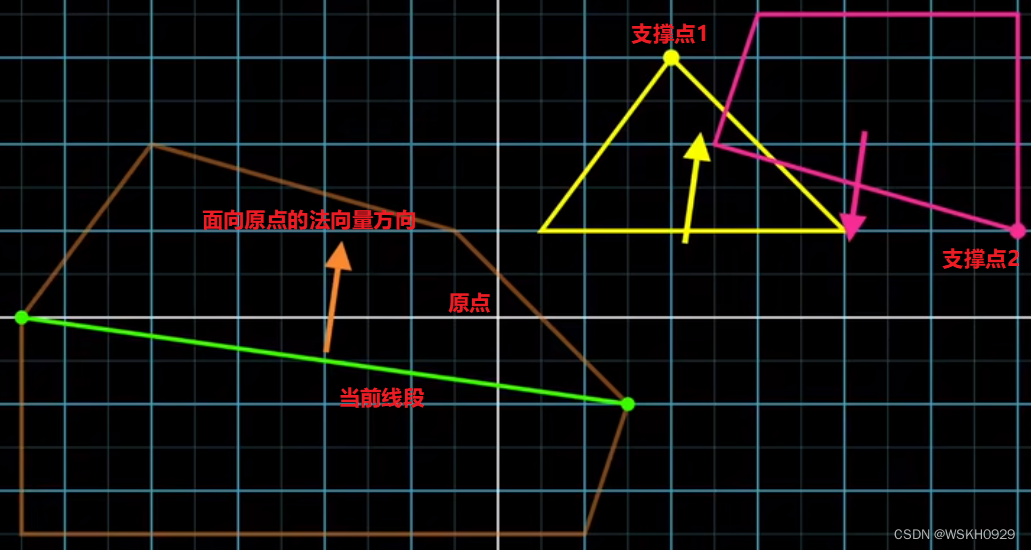
在这里插入图片描述

根据得到的两个支撑点做闵可夫斯基差，得到单纯形的第三个顶点。同样，我们做理智的检查以确保我们通过了原点。

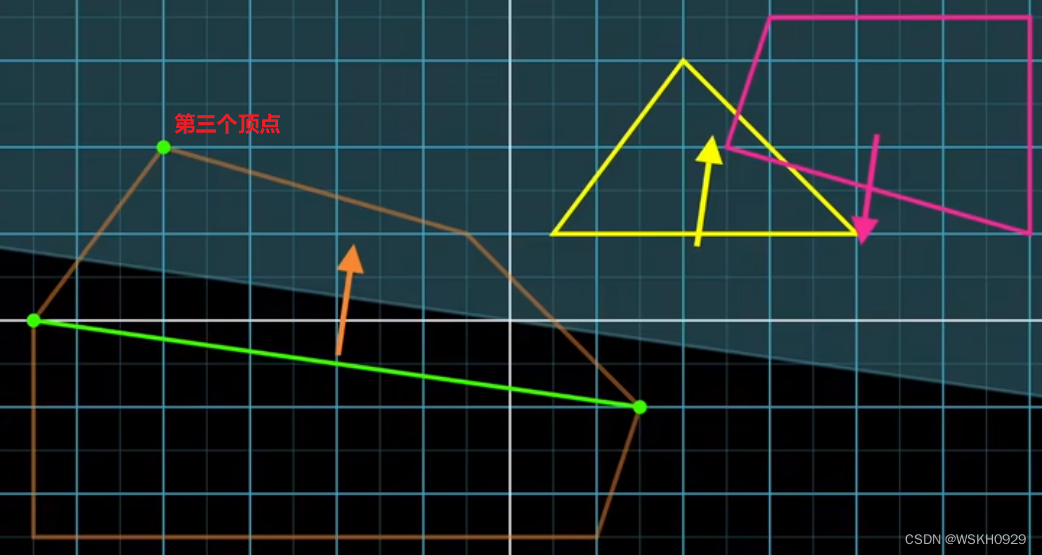
在这里插入图片描述

由于当前单纯形已经有了三个顶点，构成一个三角形，我们需要判断三角形中是否包含原点，很显然，它没有。所以我们的下一步是找到另一个新的三角形

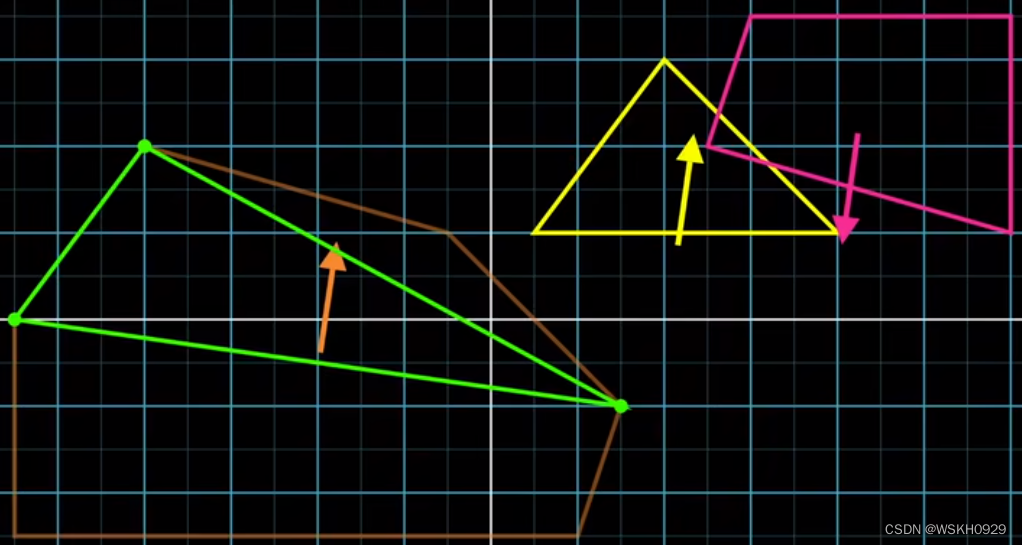
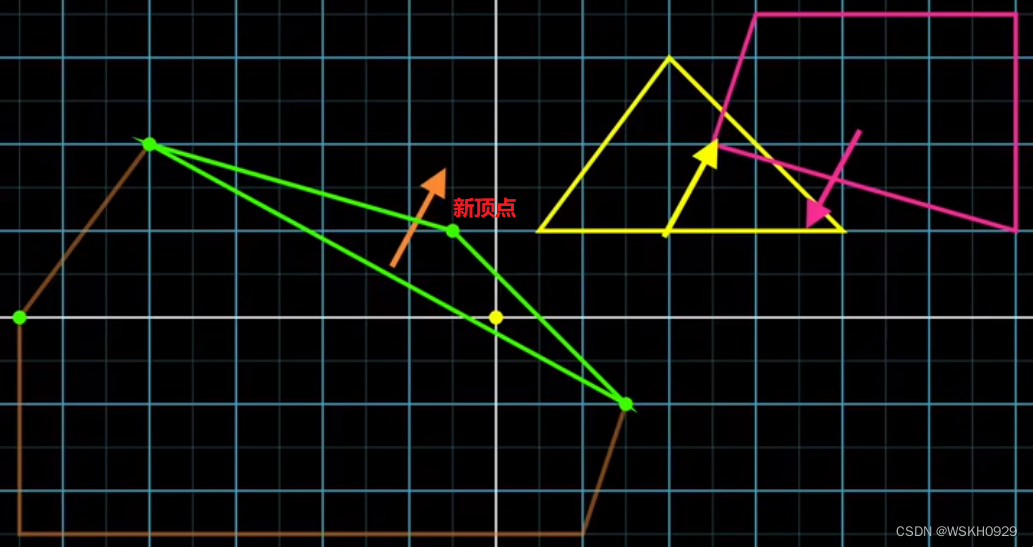
在这里插入图片描述

为了找到新的三角形，我们需要一个新的方向，GJK 选择的是当前三角形中最接近原点的边的面向原点的法向量方向，如下图所示，我们可以得到新的顶点。然后用新的顶点和刚刚用到的边构成新的三角形。此时，新三角形包含了原点，所以我们可以断定，两个多边形是重叠的。至此，程序结束。

在这里插入图片描述

3.1.2 多边形不重叠的情形

下面，我们观察多边形不重叠的情形，看看会发生什么

首先，我们用同样的初始化方式得到单纯形的第一个顶点

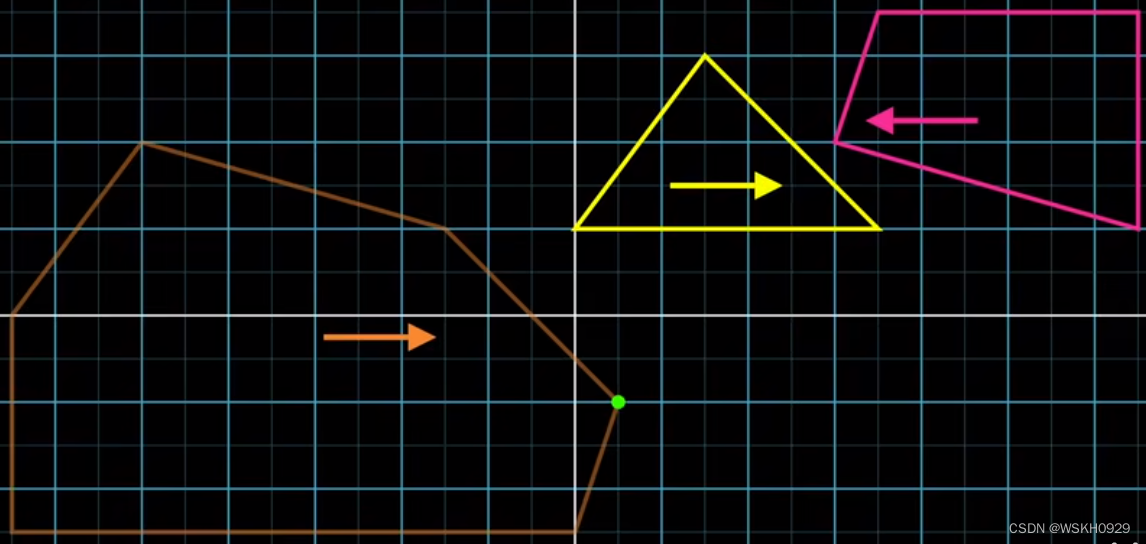
在这里插入图片描述

下一个方向是向着原点，我们可以得到第二个顶点，且这个点是经过原点的（通过了检查）

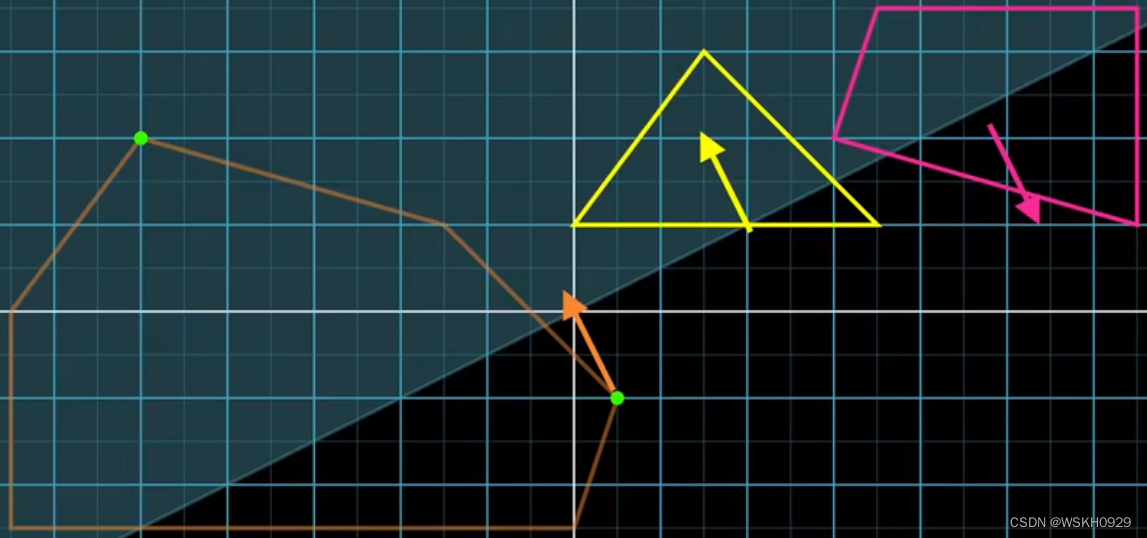
在这里插入图片描述

然后，我们根据单纯形中前两个点组成的线段的面向原点的法向量方向得到单纯形的第三个点，它也经过原点，通过了检查。

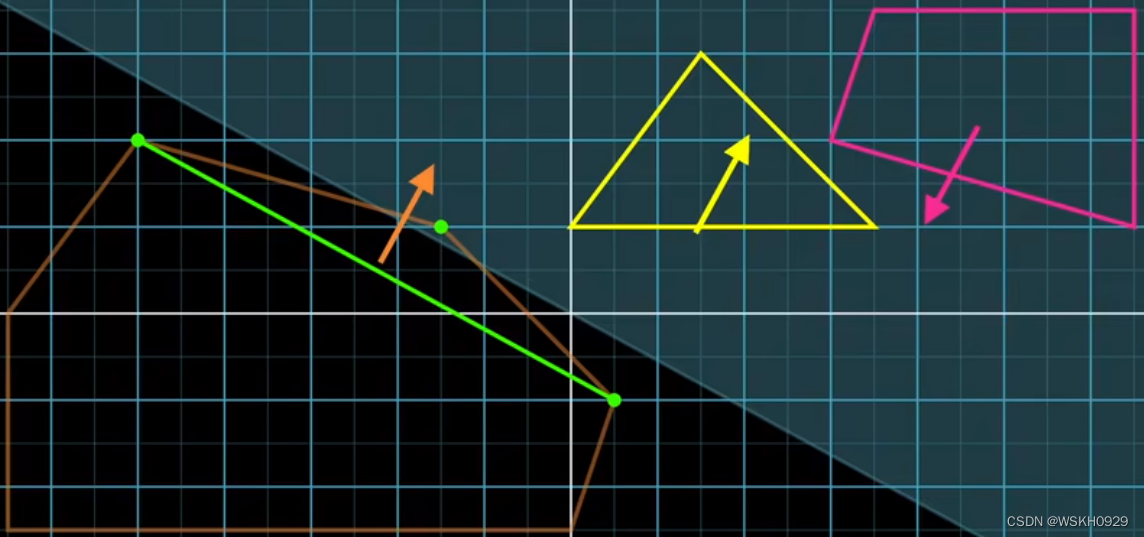
在这里插入图片描述

由于当前单纯形中已经有三个点了，所以我们可以判断它构成的三角形是否包含原点，如下图所示，三角形没有包含原点

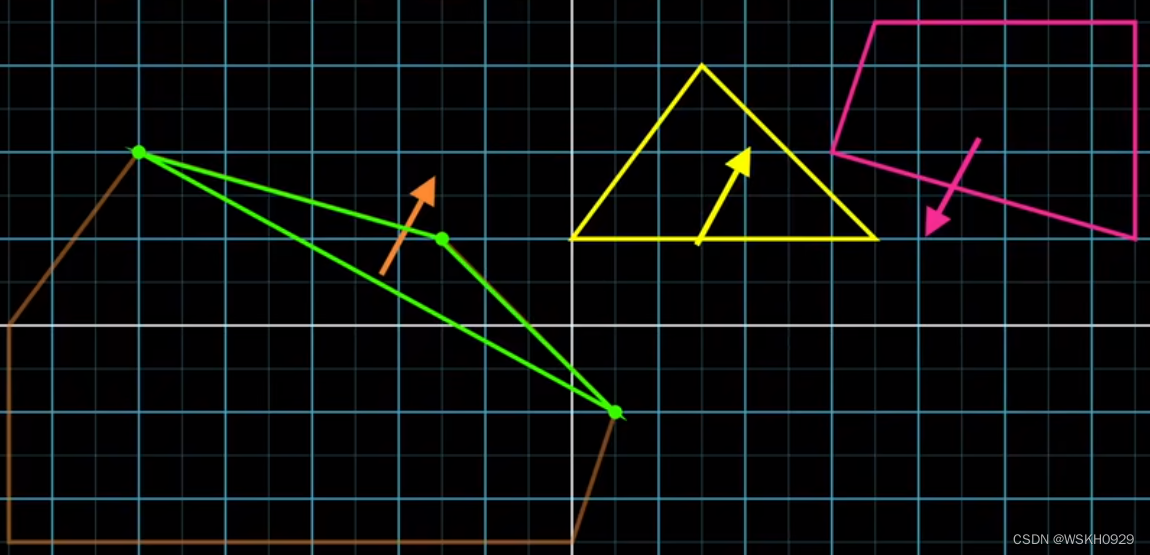
在这里插入图片描述

我们将新方向设置为三角形中最靠近原点的边的面向原点的法向量方向，然后计算出新的单纯形顶点，然而我们得到的单纯形顶点已经存在于当前单纯形中了，所以我们可以断定两个多边形肯定没有重叠。至此，程序结束。

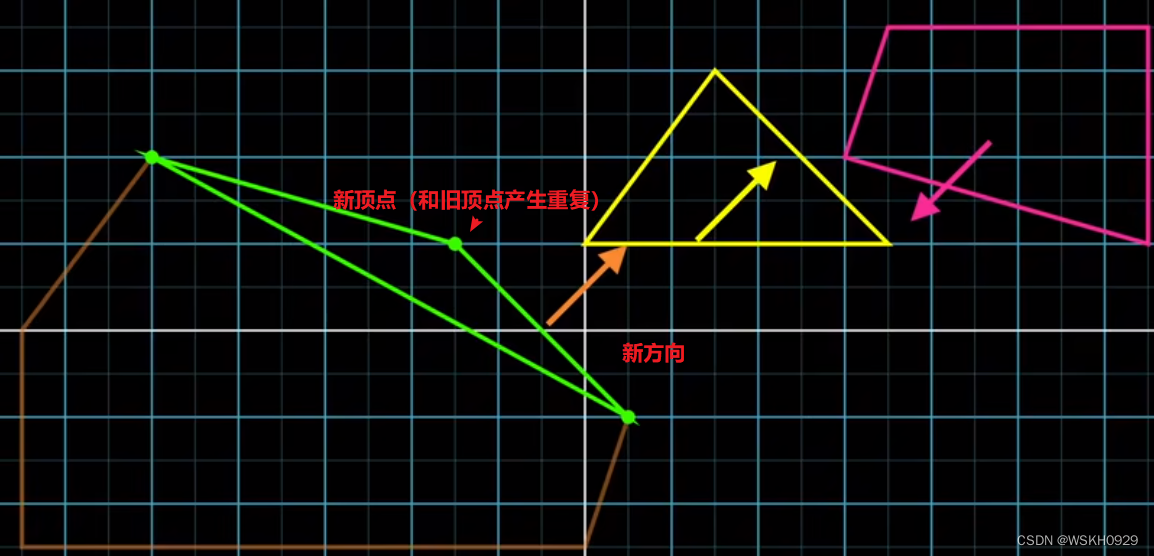
在这里插入图片描述

3.2 总结 GJK 算法步骤

  1. 通过随机的方式获取初始方向
  2. 根据初始方向，用 Support 函数分别得到两个多边形的支撑点，再做闵可夫斯基差，获得第一个顶点，并放到单纯形中
  3. 以第一个顶点面向原点的方向作为第二次迭代方向
  4. 根据第二次迭代方向，用 Support 函数分别得到两个多边形的支撑点，再做闵可夫斯基差，获得第二个顶点，此时对第二个顶点做过原点检查，如果没有通过检查则能够断定两个多边形没有重叠（程序结束），否则继续下面的步骤
  5. 将第二个顶点加入单纯形
  6. 以第一个和第二个顶点构成的线段的面向原点的法向量方向作为第三次迭代的方向
  7. 根据第三次迭代方向，用 Support 函数分别得到两个多边形的支撑点，再做闵可夫斯基差，获得第三个顶点，此时对第三个顶点做过原点检查，如果没有通过检查则能够断定两个多边形没有重叠（程序结束），否则继续下面的步骤
  8. 将第三个顶点加入单纯形
  9. 开始循环：
    • 判断当前单纯形中三个顶点组成的三角形是否包含原点，如果包含则可以断定两个多边形重叠（程序结束），否则进行下面的步骤
    • 以当前单纯形中三个顶点组成的三角形中最靠近原点的边B的面向原点的法向量方向作为下一次的迭代方向D
    • 根据迭代方向D，用 Support 函数分别得到两个多边形的支撑点，再做闵可夫斯基差，获得新的顶点
    • 对新的顶点做过原点检查，如果没有通过检查则能够断定两个多边形没有重叠（程序结束），否则继续下面的步骤
    • 如果新的顶点已经存在于当前单纯形，那么可以断定两个多边形没有重叠（程序结束），否则继续下面的步骤
    • 以新的顶点和边B的两个端点构成新的单纯形，返回到循环的第一步

3.3 讲解 GJK 算法细节

3.3.1 如何检查新的顶点是否过原点？

如下图所示，如果我们要判断A点相对B点是否过了原点，那么就可以判断原点指向A点的向量和B点指向原点的向量的点乘是否小于0，如果小于0，则A没过原点，否则A过原点。

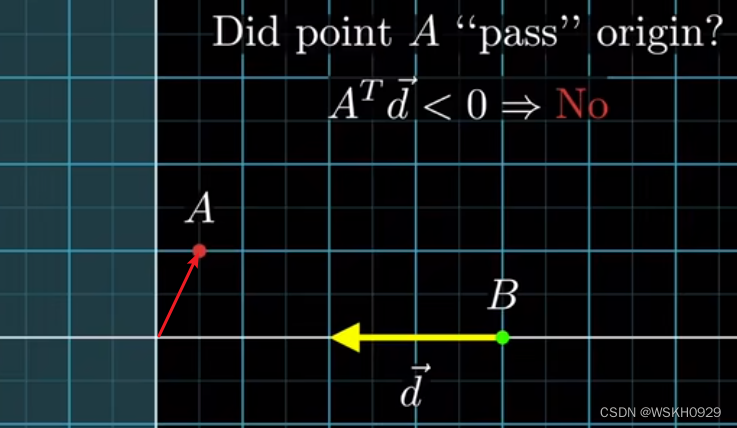
在这里插入图片描述

3.3.2 如何找到一条边面向原点的法向量方向？

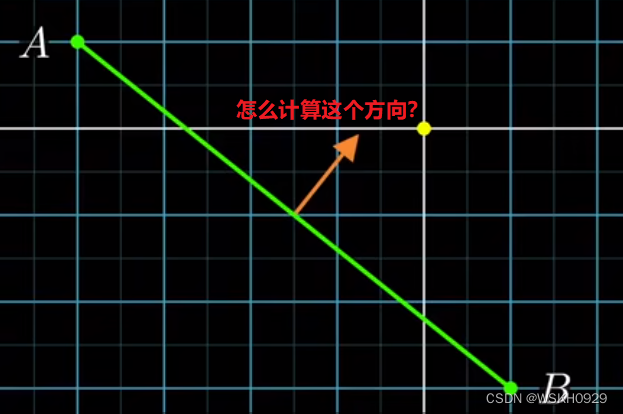
在这里插入图片描述

首先我们定义两个向量 AO 和 AB，如下图所示

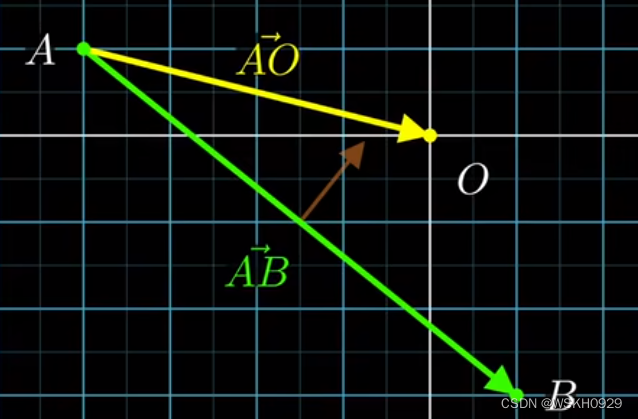
在这里插入图片描述

我们可以通过 AO 和 AB 的叉乘，找到他们的所在平面的法向量方向，如下图所示

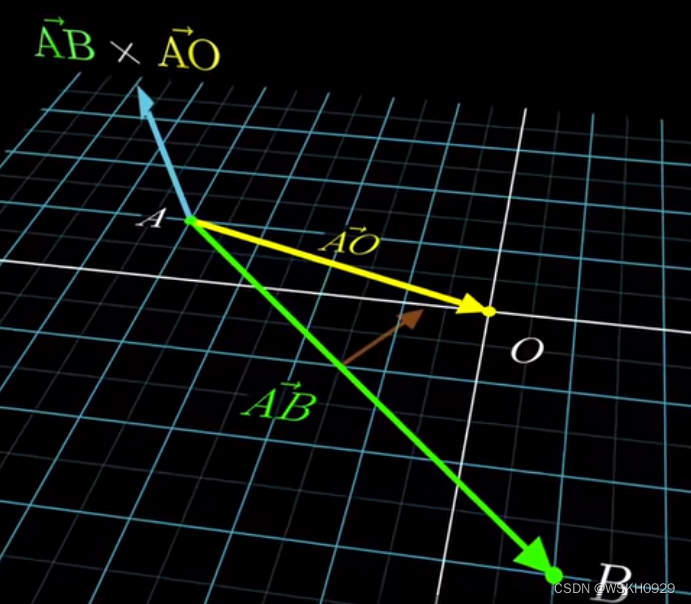
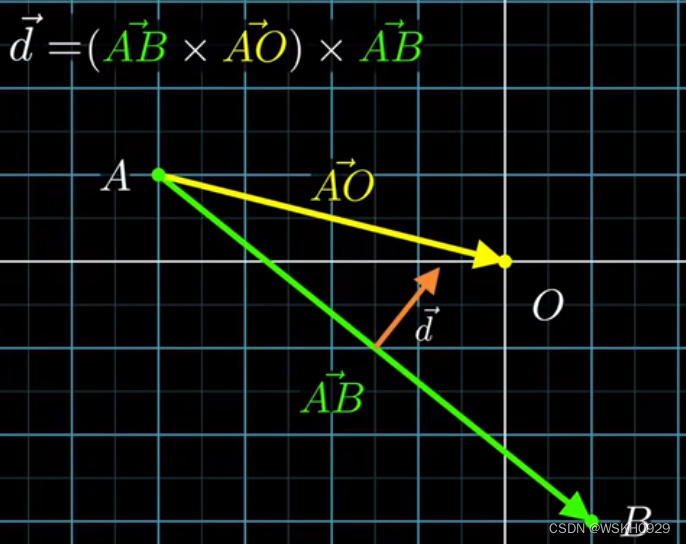
在这里插入图片描述

然后再将上一步的结果和 AB 做叉乘，就可以得到指向原点的目标方向。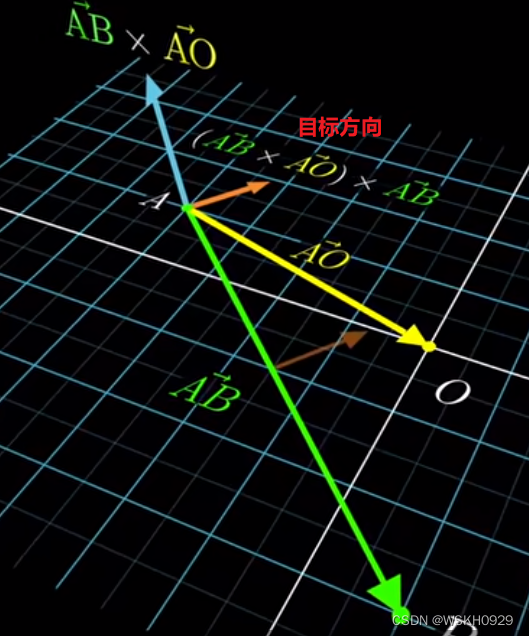
在这里插入图片描述

这种方法被称为矢量三重积

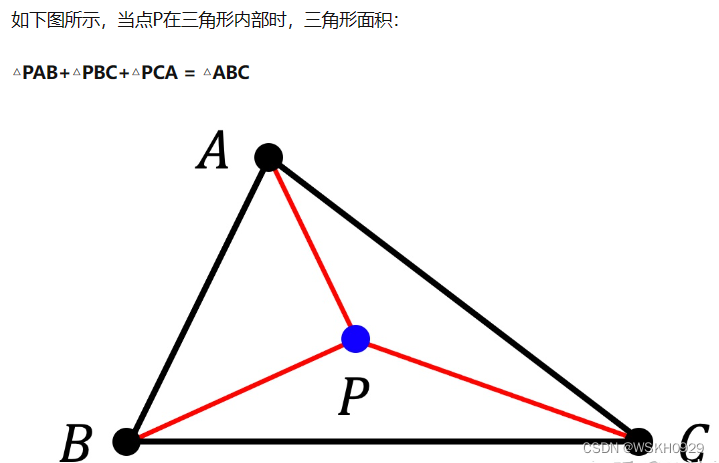
在这里插入图片描述

3.3.3 如何判断一点是否在三角形内部？

可以采用三角形面积法进行判断。

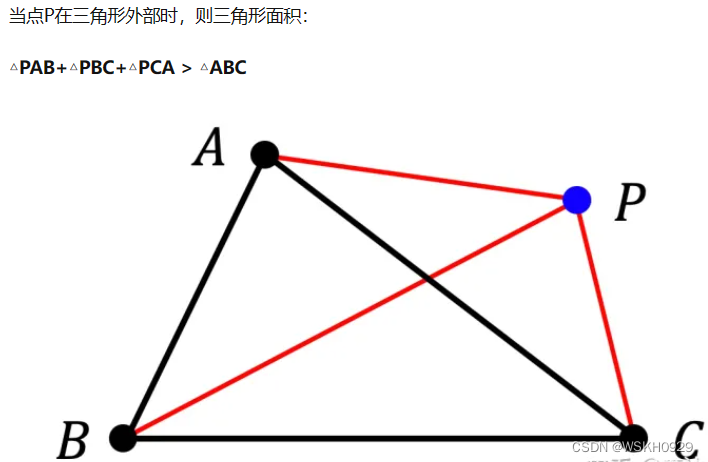
在这里插入图片描述
在这里插入图片描述

计算三角形面积可以采用海伦公式

在这里插入图片描述

3.3.4 如何找到三角形中离原点最近的边？

首先，我们要了解，如何计算原点到边的距离。

要计算点到边的距离，在二维情形下可以很简单的用点到直线距离公式求得。

但是我们要先根据边的两个端点，获取直线方程

设边的两个端点坐标分别为 （ x 1 ， y 1 ）（ x 2 ， y 2 ） （x_1，y_1）（x_2，y_2） （x1​，y1​）（x2​，y2​）

根据斜截式可得：

  • 求斜率： k = ( y 2 − y 1 ) / ( x 2 − x 1 ) k=(y_2-y_1)/(x_2-x_1) k=(y2​−y1​)/(x2​−x1​)

  • 再把 k k k 代入 y − y 1 = k ( x − x 1 ) y-y_1=k(x-x_1) y−y1​=k(x−x1​) 即可得到直线方程

  • 化为标准式： A x + B y + C = 0 Ax + By + C = 0 Ax+By+C=0，其中 A = k , B = − 1 , C = y 1 − k × x 1 A =k ,B =-1 ,C=y_1-k×x_1 A=k,B=−1,C=y1​−k×x1​

 设直线  L  的方程为  A x + B y + C = 0  ，点  P  的坐标为  ( x 0 , y 0 )  ，则点  P  到直线  L  的距离为:  ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 \text { 设直线 } \mathrm{L} \text { 的方程为 } \mathrm{Ax}+\mathrm{By}+\mathrm{C}=0 \text { ，点 } \mathrm{P} \text { 的坐标为 }(\mathrm{x} 0, \mathrm{y} 0) \text { ，则点 } \mathrm{P} \text { 到直线 } \mathrm{L} \text { 的距离为: } \frac{\left|A x_0+B y_0+C\right|}{\sqrt{A^2+B^2}}  设直线 L 的方程为 Ax+By+C=0 ，点 P 的坐标为 (x0,y0) ，则点 P 到直线 L 的距离为: A2+B2​∣Ax0​+By0​+C∣​

C++代码实现：

/* 传入三个点，计算点p0到p1和p2构成的边的距离 */ double calcPointToLineDistance(double* p0,double* p1,double* p2){ 	double k = (p2[1] - p1[1]) / (p2[0] - p1[0]); 	double A = k; 	double B = -1; 	double C = p1[1] - k * p1[0]; 	return abs(A * p0[0] + B * p0[1] + C) / sqrt(A*A+B*B); }

知道如何计算计算原点到边的距离之后，我们只需要对三角形的三条边进行遍历，即可找到离原点最近的边了。

四、C++ 完整代码（含测试样例）

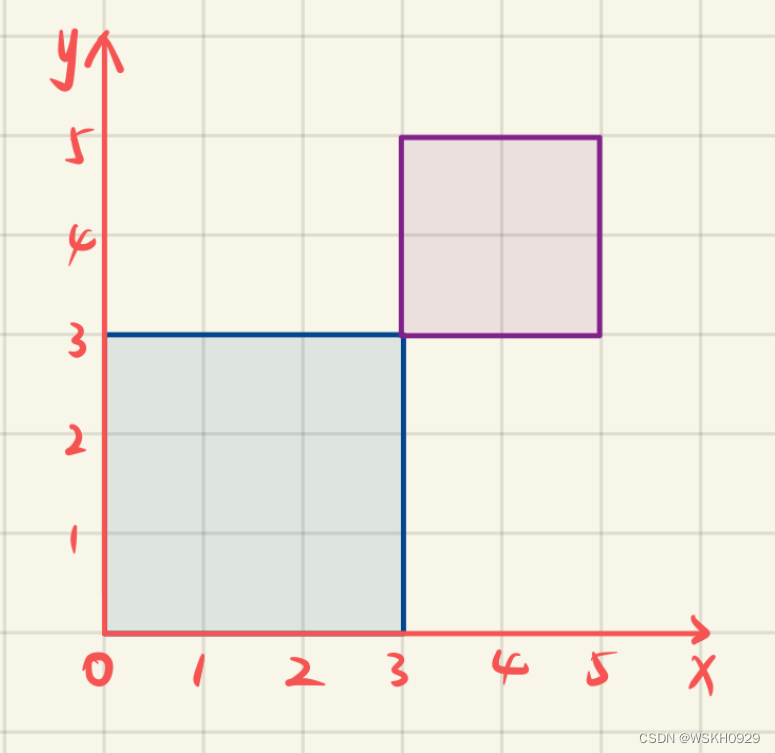
/* 描述：本代码实现了GJK算法求解二维情形下两个凸多边形的重叠判断问题 时间：2023-1-21 15:41 作者：WSKH 博客：wskh0929.blog.csdn.net */  #include <iostream> #include <vector> // 圆周率 #define PI acos(-1) // 浮点型误差精度 #define ERROR 0.0000001 using namespace std;  // 原点坐标 double* origin = new double[]{0, 0};  /* 打印单纯形信息 */ void printSimplex(int epoch, vector<double*> simplex){ 	cout << "---------------------------------- 第 " << epoch << " 次迭代 , 单纯形的顶点信息 ----------------------------------" << endl; 	for (int i = 0; i < simplex.size(); i++){ 		cout << "(" <<simplex[i][0] << " , " << simplex[i][1] << ")" << endl; 	} }  /* 打印终止信息 flag = 0: 过原点检查不通过，提前返回 false flag = 1: 三角形包含原点，提前返回 true flag = 2: 新顶点重复存在，提前返回 false */ void printStopInfo(int epoch, int flag){ 	cout << "第 " << epoch << " 次迭代："; 	switch (flag) 	{ 	case 0: 		cout << "过原点检查不通过，提前返回 false" << endl; 		break; 	case 1: 		cout << "三角形包含原点，提前返回 true" << endl; 		break; 	case 2: 		cout << "新顶点重复存在，提前返回 false" << endl; 		break; 	default: 		break; 	} }  /* 判断两个二维向量/点是否相等 */ bool isEquals(double* p1,double* p2){ 	return abs(p1[0] - p2[0]) < ERROR && abs(p1[1] - p2[1]); }  /* 计算两个点的距离 */ double calcPointToPointDistance(double* p1, double* p2){ 	return sqrt(pow(p1[0] - p2[0],2) + pow(p1[1] - p2[1],2)); }  /* 二维向量相减 */ double* diff(double* v1, double* v2){ 	return new double[]{v1[0] - v2[0], v1[1] - v2[1]}; }  /* 二维向量相加 */ double* sum(double* v1, double* v2){ 	return new double[]{v1[0] + v2[0], v1[1] + v2[1]}; }  /* 二维向量叉乘 */ double product(double* v1,double* v2){ 	return v1[0] * v2[1] - v1[1] * v2[0]; }  /* 二维向量点乘 */ double dot(double* v1, double* v2){ 	return v1[0] * v2[0] + v1[1] * v2[1]; }  /* 三维向量叉乘 */ double* product3D(double* v1, double* v2){ 	return new double[]{v1[1] * v2[2] - v2[1] * v1[2],-(v1[0] * v2[2] - v2[0] * v1[2]),v1[0] * v2[1] - v2[0] * v1[1]}; }  /* 判断一个多边形是否为凸多边形 */ bool isConvex(vector<double*> poly){ 	// 判断多边形是否为顺时针 	bool clockwise = product(new double[]{poly[1][0] - poly[0][0], poly[1][1] - poly[0][1]}, new double[]{-1, 0}) >= 0; 	for (int i = 0; i < poly.size(); i++){ 		double d = i + 1 < poly.size() ? product(poly[i], poly[i + 1]) : product(poly[i], poly[0]); 		if ((clockwise && d > 0) || (!clockwise && d < 0)){ 			return false; 		} 	} 	return true; }  /* Support 函数（常规多边形） */ double* support(vector<double*> poly, double* direction){ 	int maxIndex = 0; 	double maxDot = dot(new double[]{poly[0][0], poly[0][1]}, direction); 	for (int i = 1; i < poly.size(); i++){ 		double d = dot(new double[]{poly[i][0], poly[i][1]}, direction); 		if (d > maxDot){ 			maxDot = d; 			maxIndex = i; 		} 	} 	return new double[]{poly[maxIndex][0], poly[maxIndex][1]}; }  /* 计算两个二维向量的夹角（度）[0,PI] */ double calc2DVectorsAngle(double* v1, double* v2){ 	double d1 = sqrt(pow(v1[0] - 0, 2) + pow(v1[1] - 0, 2)); 	double d2 = sqrt(pow(v2[0] - 0, 2) + pow(v2[1] - 0, 2)); 	// 获取弧度夹角 [0,PI] 	return acos((v1[0] * v2[0] + v1[1] * v2[1]) / (d1*d2)); }  /* Support 函数（圆形） */ double* supportCircle(double* centerPoint,double r, double* direction){ 	// 获取theta 	double theta = calc2DVectorsAngle(direction, new double[]{1, 0}); 	if (direction[1] < 0){ 		theta = 2 * PI - theta; 	} 	// 根据圆的参数方程返回支撑点 	return new double[]{centerPoint[0] + r * cos(theta), centerPoint[1] + r * sin(theta)}; }  /* Support 函数（椭圆形） */ double* supportEillpse(double* centerPoint, double a,double b, double* direction){ 	// 获取theta 	double theta = calc2DVectorsAngle(direction, new double[]{1, 0}); 	if (direction[1] < 0){ 		theta = 2 * PI - theta; 	} 	// 根据椭圆的参数方程返回支撑点 	return new double[]{centerPoint[0] + a * cos(theta), centerPoint[1] + b * sin(theta)}; }  /* 根据给定方向和多边形，获取单纯形新顶点 */ double* getNewVertex(vector<double*> poly1, vector<double*> poly2, double* direction){ 	double* supportPoint1 = support(poly1, direction); 	double* supportPoint2 = support(poly2, new double[]{-direction[0], -direction[1]}); 	return diff(supportPoint1, supportPoint2); }  /* 获取初始方向 */ double* getInitDirection(){ 	return new double[]{1, 0}; }  /* 判断两个点是否过原点 */ bool isCrossingOrigin(double* A,double* B){ 	return dot(A, diff(origin, B)) >= 0; }  /* 传入三个点，计算点p0到p1和p2构成的边的距离 */ double calcPointToLineDistance(double* p0,double* p1,double* p2){ 	double k = (p2[1] - p1[1]) / (p2[0] - p1[0]); 	double A = k; 	double B = -1; 	double C = p1[1] - k * p1[0]; 	return abs(A * p0[0] + B * p0[1] + C) / sqrt(A*A+B*B); }  /* 传入两个点，获取它构成的边面向原点的法向量 */ double* getLineFaceToOriginVector(double* A, double* B){ 	double* AB = diff(B, A); 	double* AO = diff(origin, A); 	double* res = product3D(new double[]{AB[0], AB[1], 0}, new double[]{AO[0], AO[1],0}); 	return product3D(res, new double[]{AB[0], AB[1], 0}); }  /* 传入三个点，根据海伦公式计算三角形面积 */ double calcTriangleArea(double* p1, double* p2, double* p3){ 	double a = calcPointToPointDistance(p1, p2); 	double b = calcPointToPointDistance(p1, p3); 	double c = calcPointToPointDistance(p2, p3); 	double p = (a + b + c) / 2.0; 	return sqrt(p*(p-a)*(p-b)*(p-c)); }  /* 传入三个点，判断由三个点组成的三角形是否包含原点 */ bool isContainOrigin(double* p1, double* p2, double* p3){ 	double s1 = calcTriangleArea(origin,p1,p2); 	double s2 = calcTriangleArea(origin, p1, p3); 	double s3 = calcTriangleArea(origin, p2, p3); 	double s = calcTriangleArea(p1, p2, p3); 	return abs(s1 + s2 + s3 - s) < ERROR; }  /* GJK算法（返回两个多边形是否重叠） */ bool GJK(vector<double*> poly1, vector<double*> poly2){ 	// 初始化单纯形 	vector<double*> simplex; 	// 第1次迭代 	double* direction = getInitDirection(); 	double* vertex = getNewVertex(poly1,poly2,direction); 	simplex.push_back(vertex); 	printSimplex(1, simplex); 	// 第2次迭代 	direction = diff(origin, vertex); 	vertex = getNewVertex(poly1, poly2, direction); 	// 过原点检查 	if (!isCrossingOrigin(simplex[0], vertex)){ 		printStopInfo(2, 0); 		return false; 	} 	simplex.push_back(vertex); 	printSimplex(2, simplex); 	// 第3次迭代 	direction = getLineFaceToOriginVector(simplex[1], simplex[0]); 	vertex = getNewVertex(poly1, poly2, direction); 	// 过原点检查 	if (!isCrossingOrigin(simplex[0], vertex)){ 		printStopInfo(3, 0); 		return false; 	} 	simplex.push_back(vertex); 	printSimplex(3, simplex); 	// 开始循环 	for (int epoch = 4;; epoch++){ 		// 判断当前单纯形的三个顶点组成的三角形是否包含原点 		if (isContainOrigin(simplex[0], simplex[1], simplex[2])){ 			printStopInfo(epoch - 1, 1); 			return true; 		} 		// 找到三角形离原点最近的边 		double minDistance; 		int minIndex1 = -1; 		int minIndex2 = -1; 		for (int i = 0; i < simplex.size(); i++){ 			for (int j = i + 1; j < simplex.size(); j++){ 				double distance = calcPointToLineDistance(origin, simplex[i], simplex[j]); 				if (minIndex1 == -1 || distance < minDistance){ 					minDistance = distance; 					minIndex1 = i; 					minIndex2 = j; 				} 			} 		} 		// 找方向 		direction = getLineFaceToOriginVector(simplex[minIndex1], simplex[minIndex2]); 		vertex = getNewVertex(poly1, poly2, direction); 		// 是否存在于当前单纯形检查 		for (int i = 0; i < simplex.size(); i++){ 			if (isEquals(simplex[i], vertex)){ 				printStopInfo(epoch, 2); 				return false; 			} 		} 		// 过原点检查 		if (!isCrossingOrigin(simplex[0], vertex)){ 			printStopInfo(epoch, 0); 			return false; 		} 		// 更新单纯形 		double* vertex1 = simplex[minIndex1]; 		double* vertex2 = simplex[minIndex2]; 		simplex.clear(); 		simplex.push_back(vertex); 		simplex.push_back(vertex1); 		simplex.push_back(vertex2); 		printSimplex(epoch, simplex); 	} }  /* 程序主函数 */ int main(){ 	// 返回码 	int returnCode = 0;  	// 创建两个多边形 poly1 和 poly2 	vector<double*> poly1; 	poly1.push_back(new double[]{0,0}); 	poly1.push_back(new double[]{3,0}); 	poly1.push_back(new double[]{3,3}); 	poly1.push_back(new double[]{0,3}); 	vector<double*> poly2; 	// 重叠测试 	//poly2.push_back(new double[]{2,2}); 	//poly2.push_back(new double[]{5,2}); 	//poly2.push_back(new double[]{5,5}); 	//poly2.push_back(new double[]{2,5});  	// 不重叠测试 	poly2.push_back(new double[]{3, 3}); 	poly2.push_back(new double[]{5, 3}); 	poly2.push_back(new double[]{3, 5}); 	poly2.push_back(new double[]{3, 5});  	// 检验两个多边形是否为凸 	if (!isConvex(poly1)){ 		cout << "错误: poly1 为凹多边形" << endl; 		returnCode = -1; 	} 	if (!isConvex(poly2)){ 		cout << "错误: poly2 为凹多边形" << endl; 		returnCode = -1; 	}  	// 调用GJK算法进行重叠判断 	if (returnCode == 0){ 		bool isOverlap = GJK(poly1, poly2); 		cout << "重叠判断结果为: 两个多边形 <" << (isOverlap ? "重叠" : "未重叠") << ">" << endl; 	} 	 	system("pause"); 	return returnCode; }

4.1 重叠测试

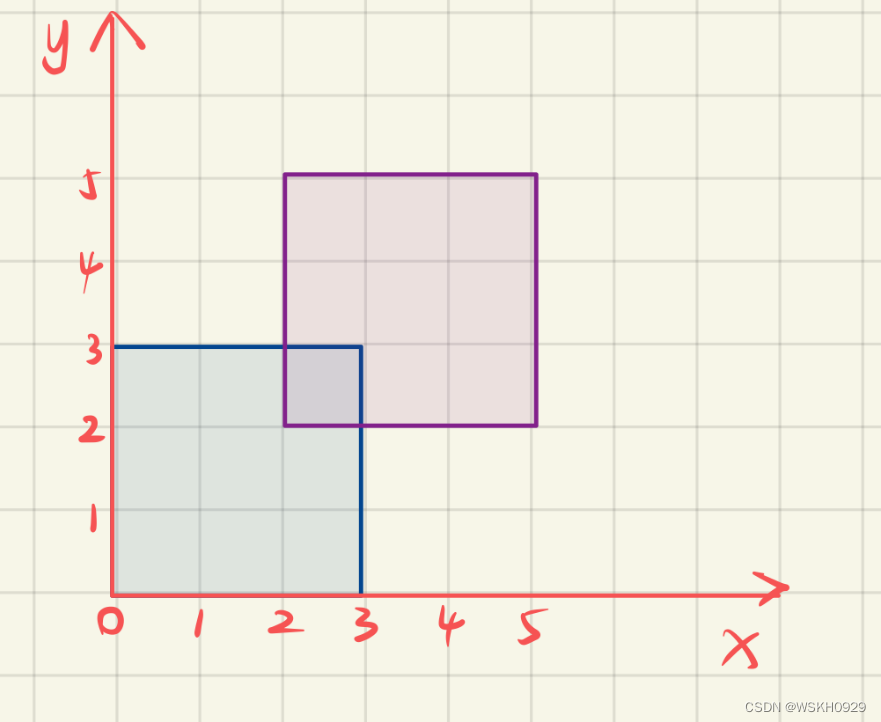
在这里插入图片描述

运行结果展示：

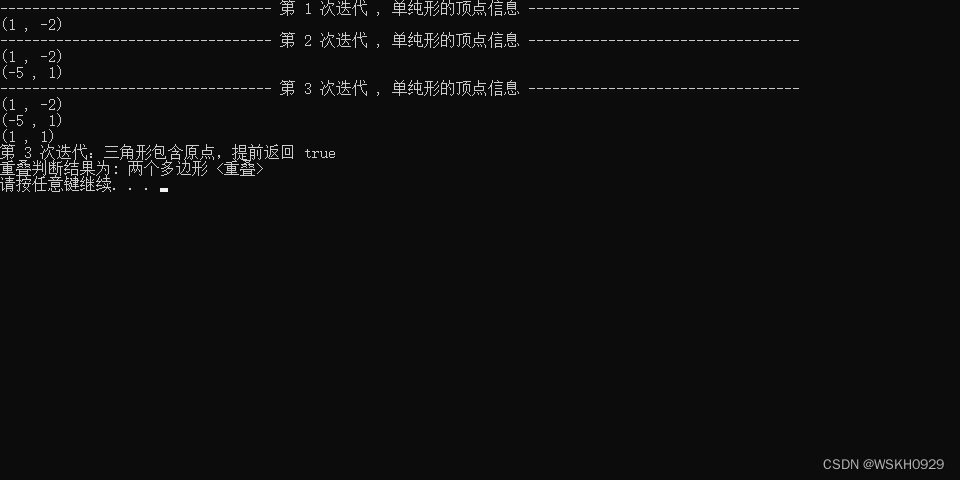
在这里插入图片描述

4.2 不重叠测试

在这里插入图片描述

在这里插入图片描述

相关阅读
  1. 如何查看和设置我的Android N设备的权限？
  2. 如何在安卓手机上自定义应用图标？
  3. 如何在安卓微信中同时听语音和查看图片？
  4. 华为哪些设备将支持升级至安卓7.0？
  5. 微信安卓软件中Q10功能有哪些独特之处？
  6. 安卓用户如何挑选最佳视频播放器应用？
  7. 安卓系统中用户文件目录的确切位置是什么？
  8. 小米4用户如何安全升级到安卓8.0系统？
  9. 如何成功将魅蓝5升级至安卓原生7.0版本？
  10. 16GB存储的安卓手机是否能满足日常需求？

广告一刻

为您即时展示最新活动产品广告消息，让您随时掌握产品活动新动态！