
🧧🧧🧧🧧🧧个人主页🎈🎈🎈🎈🎈
🧧🧧🧧🧧🧧数据结构专栏🎈🎈🎈🎈🎈
🧧🧧🧧🧧🧧【数据结构】优先级队列——堆🎈🎈🎈🎈🎈
文章目录
1. 排序的概念及引用
1.1 排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2常见排序
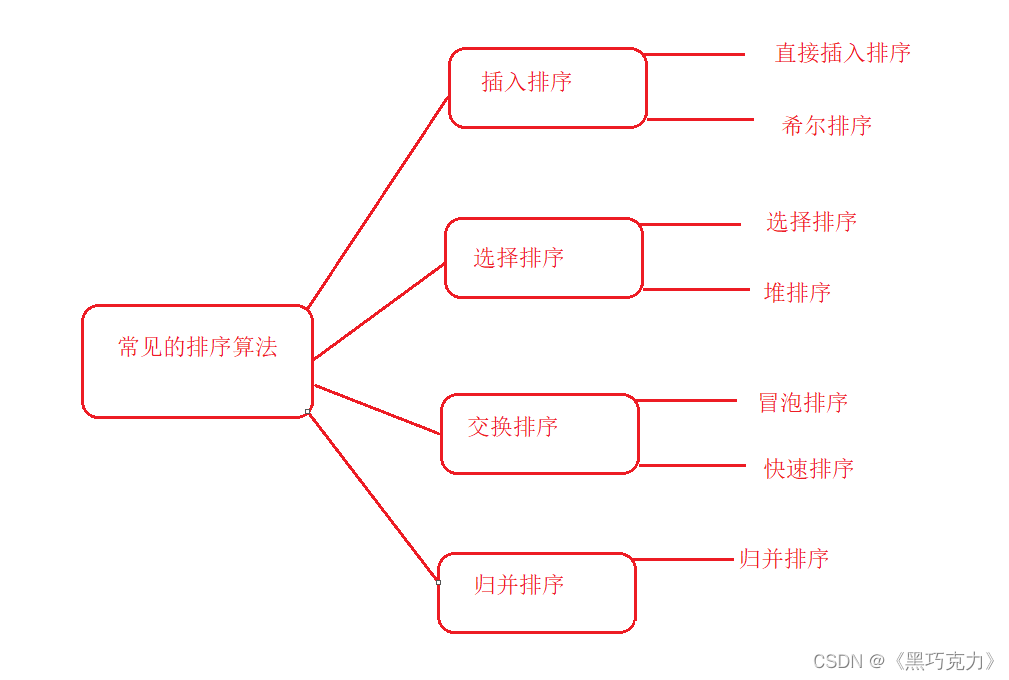
2. 常见排序算法的实现
2.1 插入排序
2.1.1基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。实际中我们玩扑克牌时,就用了插入排序的思想。
2.1.2思路分析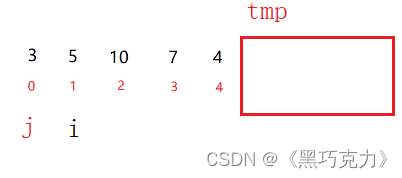
大前提:
1.我们定义一个tmp临时变量
2.定义两个指针一个i一个j,i从第二个开始,j = i -1.
1.遍历这个数组,将i下标的数值先放入tmp临时变量
2.由j下标的值与tmp中的值比较
2.1array[j] > tmp
将j下标的值放入j+1下标,然后j-1下标的值再去与tmp的值进行比较,重复这个过程,直到j下标越界,跳出这个循环
2.2array[j] < tmp
直接将tmp的值放入j+1下标中,说明j下标之前的值都是有序的
2.1.3绘图分析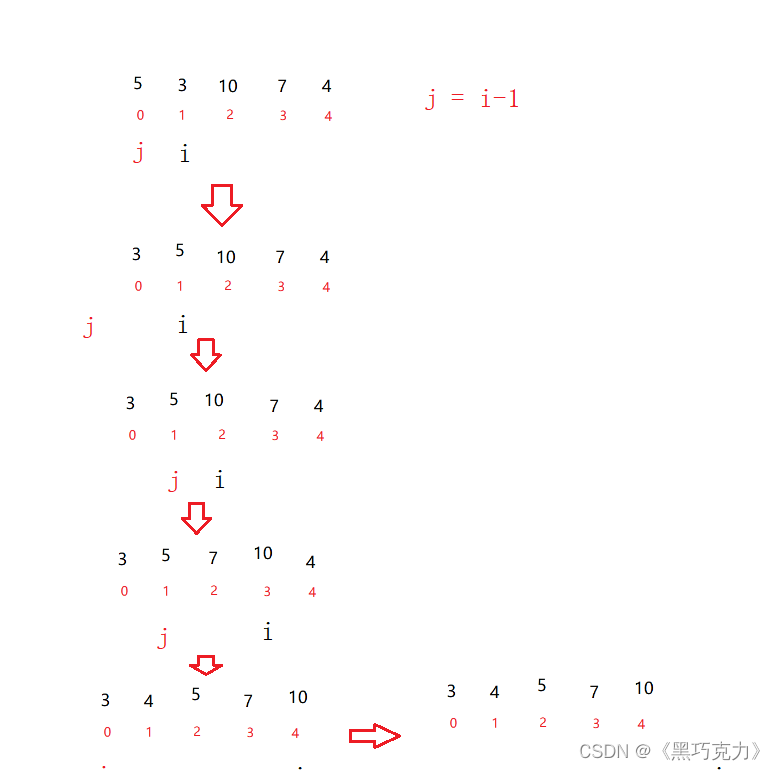
2.1.4代码实现
/** * 直接插入排序 * 时间复杂度 0(n^2) * 空间复杂度 O(1) * 稳定性:稳定的 * @param array */ public static void insertSort(int[] array) { //从数组的第二个数开始比较 for (int i = 1; i < array.length; i++) { //将i下标的元素放入临时变量tmp中 int tmp = array[i]; int j = i-1; //j是从i-1开始 for (; j >=0 ; j--) { //比较j下标的值与tmp的值 if(array[j] > tmp) { //array[j] > tmp array[j+1] = array[j]; } else { //array[j] < tmp break; } } //走到这里说明要么就是array[j] < tmp 要么就是j不满足条件 array[j+1] = tmp; } } 2.2希尔排序
2.2.1基本思想
先选定一个整数,把待排序文件中所有记录分成多个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序
2.2.2思路分析
假设数组中一共有N个数
1.先确定gap(组数),有很多种分组的方式,我举几个例子,分别为gap = N/2 和 gap = N/3+1,gap越大,组中的数据越小,一般采取跳跃式分组,这样可以使组中的数据小的放在前面,大的放在后面。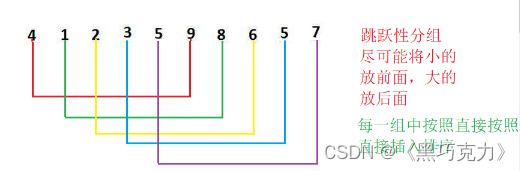
2.采取直接插入排序
3.采取直接插入排序时,i定义为gap,j定义为i-gap而每一次i++加1即可,不需要加gap,这样使得gap组可以同时进行,j在回退的过程中不能j–,必须j-=gap。
2.2.3绘图分析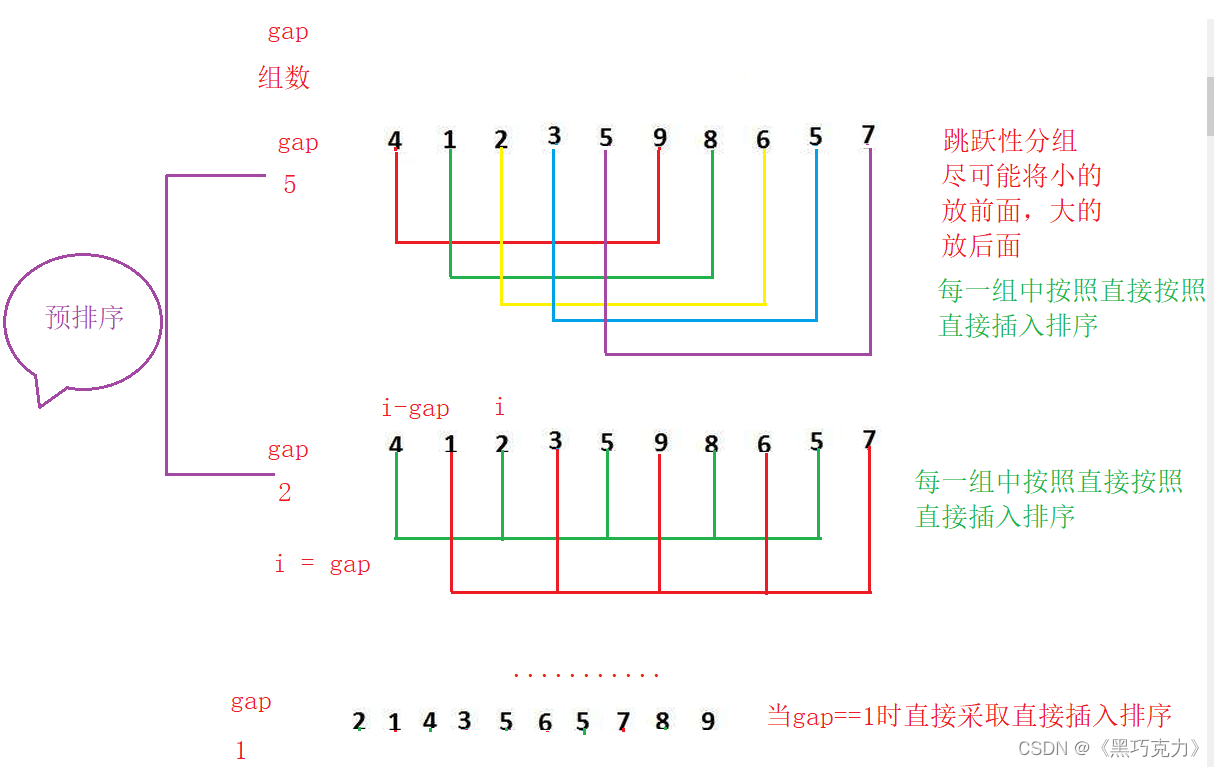
2.2.4代码实现
/** * 希尔排序 * 时间复杂对 O(n^2) * 空间复杂度 O(1) * 稳定性:不稳定 * @param array */ public static void shellSort(int[] array) { //确定分组 int gap = array.length; while(gap > 1) { gap /= 2; insertSort1(array,gap); } } private static void insertSort1(int[] array,int gap) { //从数组的第二个数开始比较 for (int i = gap; i < array.length; i++) { //将i下标的元素放入临时变量tmp中 int tmp = array[i]; int j = i-gap; //j是从i-1开始 for (; j >=0 ; j -= gap) { //比较j下标的值与tmp的值 if(array[j] > tmp) { //array[j] > tmp array[j+gap] = array[j]; } else { //array[j] < tmp break; } } //走到这里说明要么就是array[j] < tmp 要么就是j不满足条件 array[j+gap] = tmp; } } 注意:此处的gap直接会影响这个排序的时间复杂度。
2.3选择排序
2.3.1基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
2.3.2思路分析
大前提:
1.需要两个指针i,j来遍历这个数组
2.需要一个临时变量minIndex来存储数组中最小值的下标
思路分析:
1.i从0下标开始,先将i下标存储再minIndex中
2.j从i+1开始向后遍历,再遍历的过程中与minIndex下标的值比较,小于则更新minIndex之后j++,大于则直接j++
3.找到了这个数组最小值的下标,此时minIndex就是最小值的下标,然后将与i下标的值进行交换然后i++,重复上述步骤直到数组有序
2.3.3绘图分析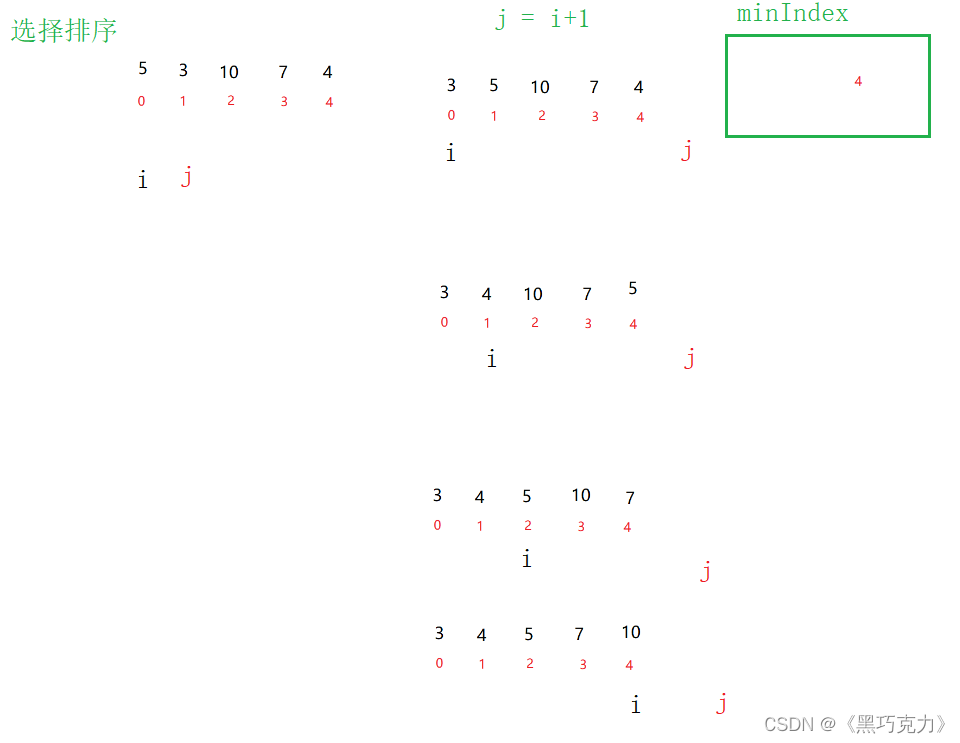
2.3.4代码实现
/** * 选择排序 * 时间复杂对 O(n^2) * 空间复杂度 O(1) * 稳定性:不稳定 * @param array */ public static void selectSort1(int[] array) { for (int i = 0; i < array.length; i++) { //先将i的下标存储再minIndex中 int minIndex = i; for (int j = i