数据结构-构造哈夫曼树【详解+代码+图示】一文解惑！

哈夫曼树 (Huffman Tree)

文章目录

• 哈夫曼树 (Huffman Tree)
• • 导论
  • 构造哈夫曼树
  • • 语言描绘
    • 图形化理解
  • 证明结论
  • 代码实现
  • 测试
  • 结果对照
  • 总结

导论

我们在学习哈夫曼树之前需要先了解 什么是哈夫曼树?

• 哈夫曼树 是一种最优树,是一类带权路径长度最短的二叉树,通过哈夫曼算法可以构建一棵哈夫曼树,利用哈夫曼树可以构造一种不等长的二进制编码,并且构造所得的哈夫曼编码是一种最优前缀码.

• 通俗来讲 : n 个带权节点均作为叶子节点,构造出的一棵带权路径长度最短的二叉树,则把这棵树称为"哈夫曼树" 、“赫夫曼树” 、“Huffman Tree” 或者 “最优二叉树” . (备注 : 本文均用 “哈夫曼树” 来称呼)

第一次接触 哈夫曼树 的小伙伴可能对上述的定义不能第一时间消化,我们可以先来明确几个学哈夫曼树之前必须掌握的几个会用到的名词的概念,把这几个概念理解透了之后会帮助你更好的认识哈夫曼树.

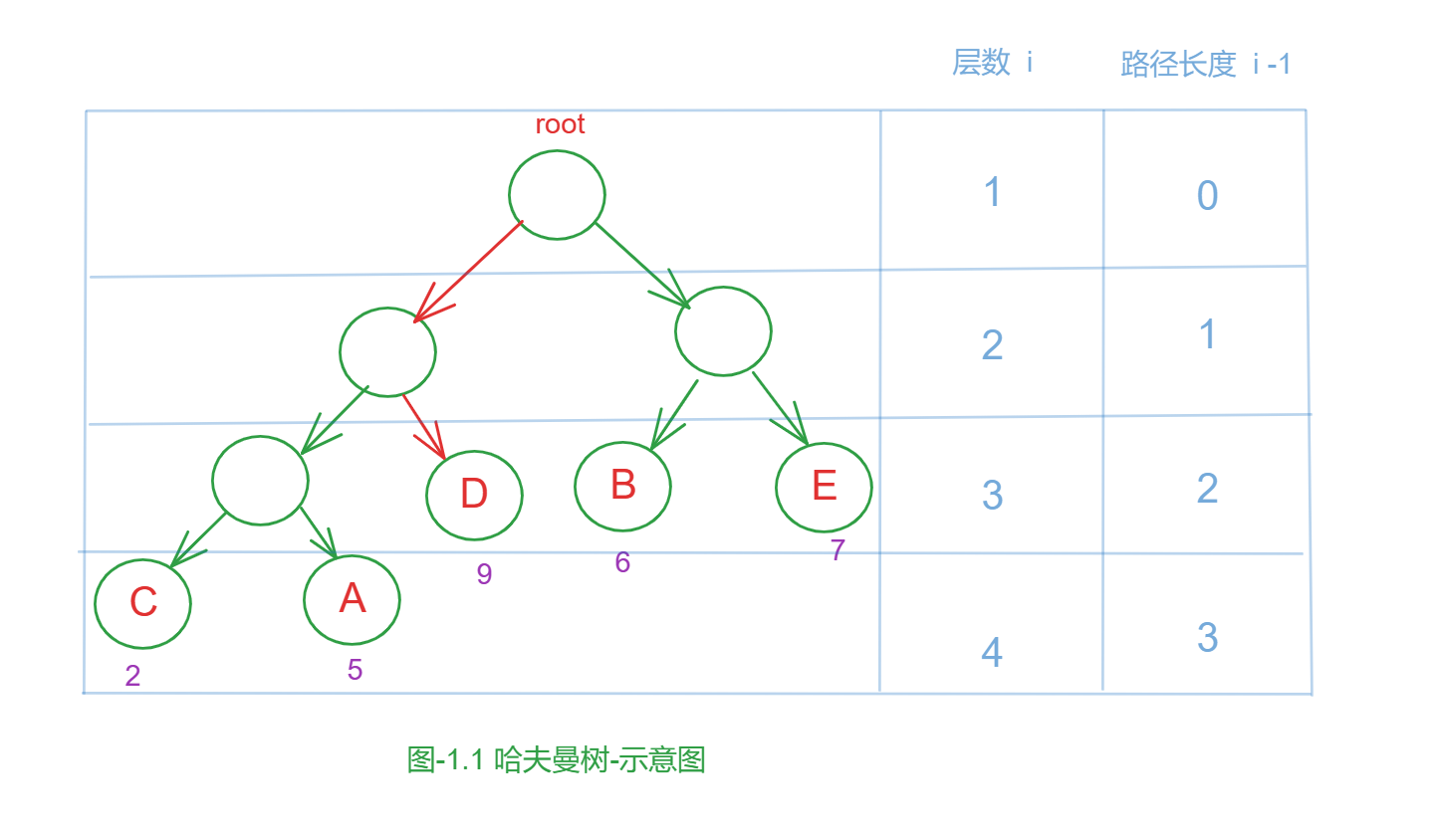
• 路径： 在一棵树中 ,从一个结点到另外一个结点的通路就称为 树的路径 .如图1.1 从根节点root到D节点之间的通路就是二叉树中的一条路径
• 路径长度 : 在路径中,每经过一个结点路径长度就加一 .如果我们规定根节点所在的树的 层数为第一层,那么从根节点出发 走到第 i 层 ,那么当前层的节点的 路径长度 等于 i-1,如图1.1所示
• 树的路径长度 : 从根节点出发到所有结点的路径长度之和.
• 结点的权值 :  一个结点的权值实际上就是这个结点子树在整个树中所占的比例. 如图1.1 所示 ,C、A、D、B、E结点的权分别为2、5、9、6、7.
• 结点的带权路径长度 : 结点到树根之间的路径长度与该结点权值的乘积.如图1.1 所示 ,D结点的带权路径长度 = 2 * 9 = 18
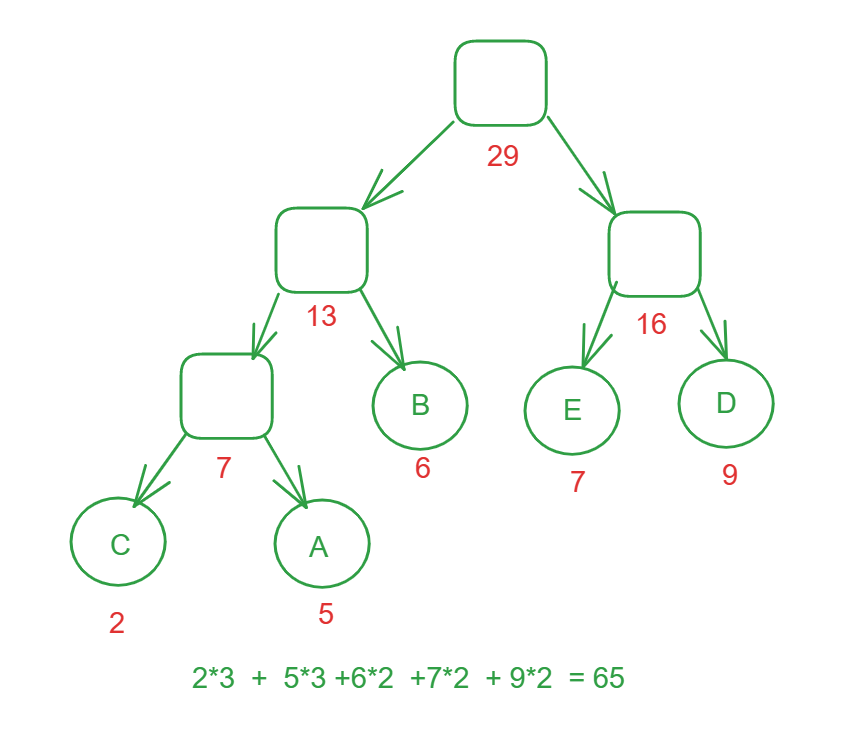
• 树的带权路径长度 ( Weighted Path Length of Tree 简称为 WPL): 树中所有叶子结点的带权路径长度之和.如图1.1 所示,该哈夫曼树的带权路径长度 WPL =2 * 3 + 5 * 3 + 9 * 2 + 6 * 2 + 7 * 2 = 65
  
  

构造哈夫曼树

要记住 哈夫曼树 中的权值越大的结点离根节点越近,权值越小的结点离根节点越远,这意味着一组带权结点构造出来的哈夫曼树中权值最小的结点离哈夫曼树最远,权值最大的结点离哈夫曼树最近,也就是我们 图1.1 中可以观察出来的.

构造哈夫曼树的过程其实就是"爸爸去哪儿"的过程.

语言描绘

• 形象叙述构造哈夫曼树的步骤

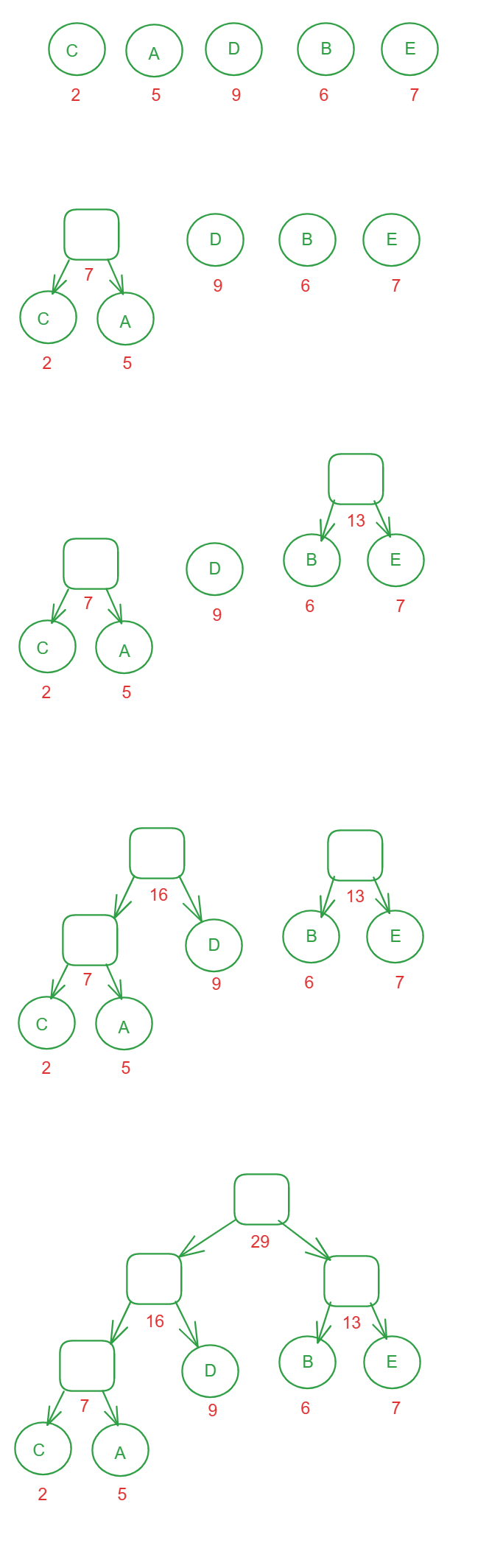
  从下往上构造,从已知的剩余权值集合中权值最小的那两个结点(如果权值相同那么直接就是相同的这两个结点),让他们成为兄弟结点,两兄弟的权值相加,合力找到父亲结点,此时父亲节点的权值就是两兄弟结点的权值的和,然后把父亲节点的权值添加到权值集合中的同时删除这两个兄弟节点,.重复循环"爸爸去哪儿"这个过程,直至权值集合中只剩下祖宗(根节点)为止. 那么这棵哈夫曼树也就构造完了.

  备注: 感觉核心就是你现在计划创建一棵二叉树,但是这棵二叉树你不能随意创建,而是要按照生成 “最优二叉树” 的规则来创建 ,这样想是不是就简单许多 ! 而这个规则就是哈夫曼算法.

  ---

• 严谨的构造哈夫曼树的步骤

对于给定的有各自权值的 n 个结点

1. 在 n 个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和；
2. 在原有的 n 个权值中删除那两个最小的权值，同时将新的权值加入到 n–2 个权值的行列中，以此类推；
3. 重复 1 和 2 ，直到所以的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树/最优二叉树。

注意:

1. 最优二叉树的形态不唯一,但是WPL最小.
2. 最优二叉树中,权越大的叶子离根越近.

图形化理解

例如: 已知权值 W = {2,5,9,6,7},请构造哈夫曼树.

证明结论

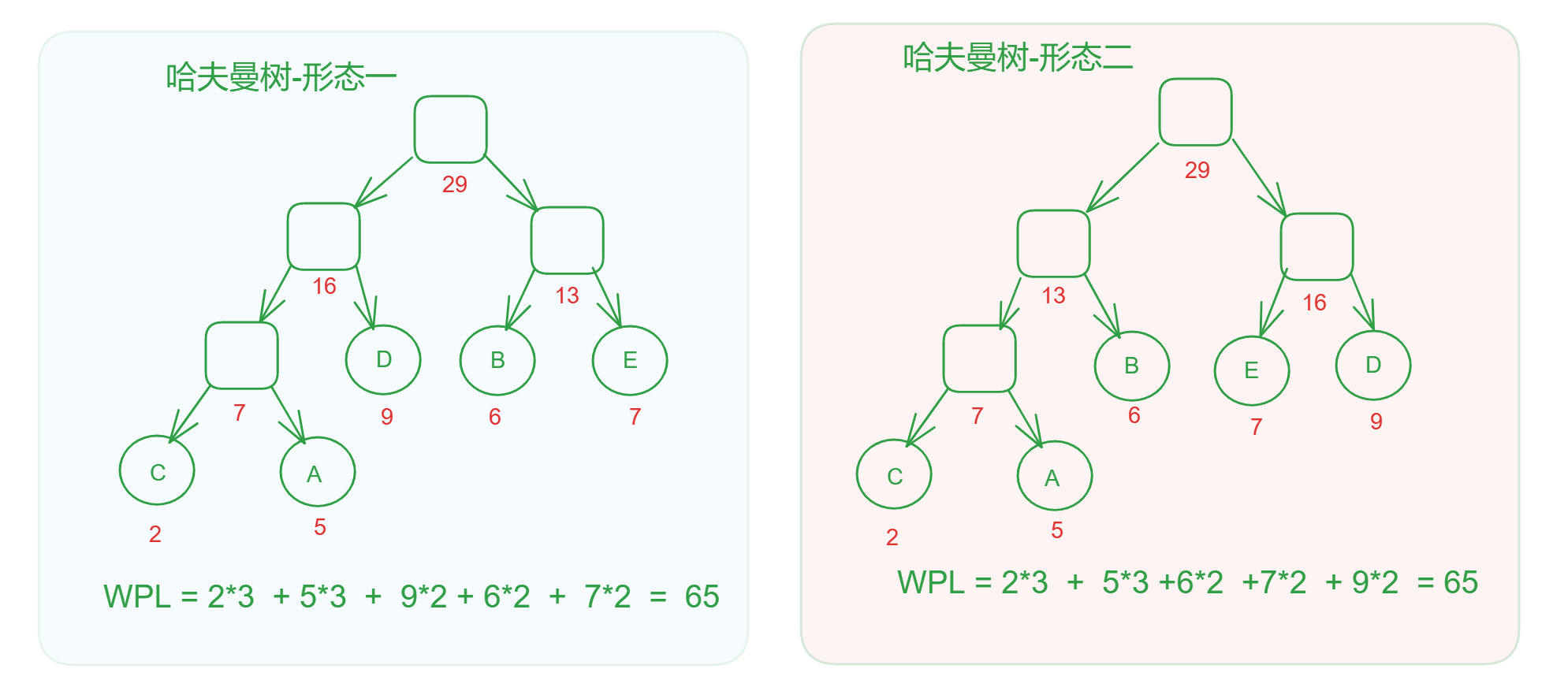
最优二叉树的形态不唯一,但是WPL最小

• 先证明第一句话: 相同的权值构造出来的哈夫曼树形态不唯一

同样是上述的例子,我们可以构造出另一种形态的哈夫曼树,同时我们可以计算出两种形态的二叉树的带权路径,看看是否相等 ?

• 然后我们来证明第二句话 : 证明哈夫曼算法构造出的哈夫曼树的WPL一定是最小的，且其他二叉树的WPL一定大于等于哈夫曼树的WPL。

1. 定义：

• 带权路径长度（WPL）是指每个叶子节点的权值乘以其深度的总和。

2. 引理：

• 对于任意的二叉树，交换任意两个叶子节点的位置，WPL都会增加。

3. 证明：

• 哈夫曼树的构造过程：

  1. 哈夫曼算法每次选择权值最小的两个节点合并，构造出一颗二叉树。
  2. 重复这个过程，直到所有节点合并成一个根节点，形成哈夫曼树。

• 交换叶子节点的影响：

  • 考虑哈夫曼树的构造过程，每次选择最小的两个节点合并，如果我们交换了两个叶子节点的位置，这两个节点的权值就不再是最小的了。
  • 在构造过程中，我们总是选择权值最小的节点，因此交换叶子节点位置后，这两个节点的合并会在构造树的过程中晚一些，导致它们在更深的层次上，从而增加了WPL。

  如果这里不懂这里的影响是什么,我会再下一篇的博客中详细解释,这涉及到了 贪心策略

• 结论：

  • 由于哈夫曼算法保证了每次合并都选择最小权值的节点，任何对于叶子节点位置的交换都会导致合并发生在更深的层次上，增加WPL。
  • 因此，哈夫曼树的构造方式保证了WPL最小。

4. 总结：

• 哈夫曼树的构造方式保证了每次合并都是最优的选择，从而使得整个树的WPL最小。
• 如果使用其他方式构造二叉树，由于不能保证每次都选择最小权值的节点进行合并，可能会导致WPL更大。

代码实现

在构造哈夫曼树的过程中，我们首先需要定义一个节点类来表示树的节点，然后编写一个构造哈夫曼树的算法。

1. 定义了一个HuffmanNode类，用于表示哈夫曼树的节点
2. 在HuffmanTree类中，实现一个buildHuffmanTree方法，该方法接受一个权值数组
3. 使用优先队列来构造哈夫曼树
4. 通过main方法演示了如何使用这个方法来构造哈夫曼树

这个实现涉及到了优先队列（PriorityQueue），它是一个能够保证每次取出的元素都是队列中权值最小的元素的数据结构。在哈夫曼树的构建中，我们不断地合并权值最小的两个节点，而优先队列正好能够满足这个需求。

package src.test.java;  import java.util.PriorityQueue;  // 定义哈夫曼树节点类 class HuffmanNode implements Comparable<HuffmanNode> {     int weight;          // 权值     HuffmanNode left;    // 左子节点     HuffmanNode right;   // 右子节点      public HuffmanNode(int weight) {         this.weight = weight;     }      // 实现Comparable接口，用于PriorityQueue的比较     @Override     public int compareTo(HuffmanNode other) {         return this.weight - other.weight;     } }  public class HuffmanTree {      // 构造哈夫曼树的方法     public static HuffmanNode buildHuffmanTree(int[] weights) {         // 使用优先队列来存储节点，每次都取出权值最小的两个节点进行合并         PriorityQueue<HuffmanNode> pq = new PriorityQueue<>();                  // 将权值数组中的每个元素转化为节点并添加到优先队列中         for (int weight : weights) {             pq.add(new HuffmanNode(weight));         }          // 不断合并节点直到只剩一个节点，即哈夫曼树的根节点         while (pq.size() > 1) {             HuffmanNode left = pq.poll();   // 弹出权值最小的节点             HuffmanNode right = pq.poll();  // 弹出权值次小的节点              // 创建一个新节点，权值为两个子节点的权值之和             HuffmanNode parent = new HuffmanNode(left.weight + right.weight);             parent.left = left;             parent.right = right;              // 将新节点添加回优先队列             pq.add(parent);         }          // 返回哈夫曼树的根节点         return pq.poll();     }      // 打印哈夫曼树的方法（可选）     public static void printHuffmanTree(HuffmanNode root, String prefix) {         if (root != null) {             System.out.println(prefix + root.weight);             printHuffmanTree(root.left, prefix + "0");             printHuffmanTree(root.right, prefix + "1");         }     }      public static void main(String[] args) {         int[] weights = {2, 5, 9, 6, 7};          // 构造哈夫曼树         HuffmanNode root = buildHuffmanTree(weights);          // 打印哈夫曼树（可选）         printHuffmanTree(root, "");     } }  

测试

package src.test.java;  public class HuffmanTreeTest {      public static void main(String[] args) {         int[] weights = {2, 5, 9, 6, 7};          // 构造哈夫曼树         HuffmanNode root = HuffmanTree.buildHuffmanTree(weights);          // 打印哈夫曼树的结构         System.out.println("Huffman Tree Structure:");         printHuffmanTreeStructure(root, "");     }      // 递归打印哈夫曼树的结构     private static void printHuffmanTreeStructure(HuffmanNode root, String prefix) {         if (root != null) {             System.out.println(prefix + "Weight: " + root.weight);             if (root.left != null || root.right != null) {                 System.out.println(prefix + "├── Left:");                 printHuffmanTreeStructure(root.left, prefix + "│    ");                 System.out.println(prefix + "└── Right:");                 printHuffmanTreeStructure(root.right, prefix + "     ");             }         }     } }  

结果对照

• 控制台输出结果

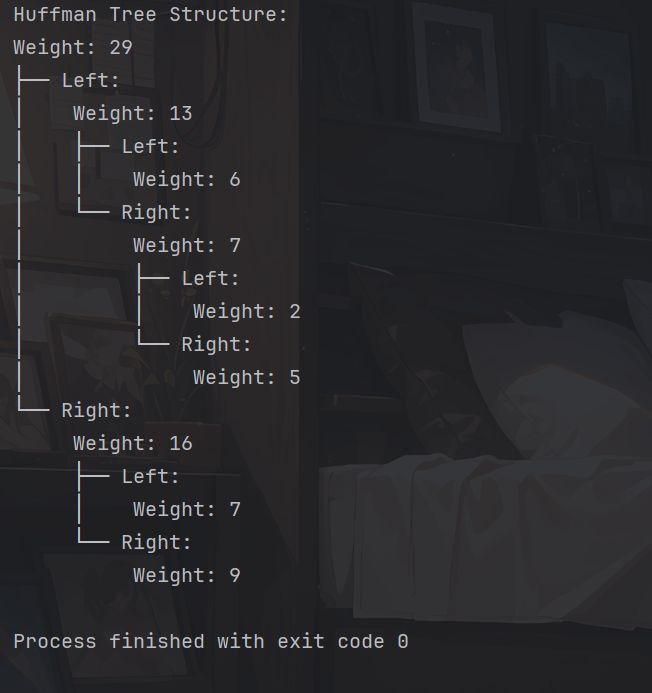
• 哈夫曼树图形

总结

1. 基础概念：深入了解了哈夫曼树的概念，包括路径、路径长度、带权路径长度等基础知识。

2. 构造过程：通过图形化和语言描述，清晰演示了从下而上构造哈夫曼树的步骤，以及最终得到最优二叉树的过程。

3. 证明方法：通过引理和推导，解释了为何哈夫曼树的构造方式能够保证带权路径长度最小，涉及到了贪心策略的应用。

4. 实际应用：通过Java代码实现展示了哈夫曼树的构造过程，将理论知识转化为实际应用，加深了对算法的理解。