阅读量:4

目录
226. 翻转二叉树
题目描述
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
做题思路
本题属于二叉树的基础题目,需要牢牢掌握。
参考代码
//DFS递归 class Solution { /** * 前后序遍历都可以 * 中序不行,因为先左孩子交换孩子,再根交换孩子(做完后,右孩子已经变成了原来的左孩子),再右孩子交换孩子(此时其实是对原来的左孩子做交换) */ public TreeNode invertTree(TreeNode root) { if (root == null) { return null; } invertTree(root.left); invertTree(root.right); swapChildren(root); return root; } private void swapChildren(TreeNode root) { TreeNode tmp = root.left; root.left = root.right; root.right = tmp; } } //BFS class Solution { public TreeNode invertTree(TreeNode root) { if (root == null) {return null;} ArrayDeque<TreeNode> deque = new ArrayDeque<>(); deque.offer(root); while (!deque.isEmpty()) { int size = deque.size(); while (size-- > 0) { TreeNode node = deque.poll(); swap(node); if (node.left != null) {deque.offer(node.left);} if (node.right != null) {deque.offer(node.right);} } } return root; } public void swap(TreeNode root) { TreeNode temp = root.left; root.left = root.right; root.right = temp; } } 101. 对称二叉树
题目描述
给你一个二叉树的根节点 root , 检查它是否轴对称。
做题思路
本题属于二叉树的基础题目,需要牢牢掌握。
参考代码
/** * 递归法 */ public boolean isSymmetric1(TreeNode root) { return compare(root.left, root.right); } private boolean compare(TreeNode left, TreeNode right) { if (left == null && right != null) { return false; } if (left != null && right == null) { return false; } if (left == null && right == null) { return true; } if (left.val != right.val) { return false; } // 比较外侧 boolean compareOutside = compare(left.left, right.right); // 比较内侧 boolean compareInside = compare(left.right, right.left); return compareOutside && compareInside; } /** * 迭代法 * 使用双端队列,相当于两个栈 */ public boolean isSymmetric2(TreeNode root) { Deque<TreeNode> deque = new LinkedList<>(); deque.offerFirst(root.left); deque.offerLast(root.right); while (!deque.isEmpty()) { TreeNode leftNode = deque.pollFirst(); TreeNode rightNode = deque.pollLast(); if (leftNode == null && rightNode == null) { continue; } // if (leftNode == null && rightNode != null) { // return false; // } // if (leftNode != null && rightNode == null) { // return false; // } // if (leftNode.val != rightNode.val) { // return false; // } // 以上三个判断条件合并 if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) { return false; } deque.offerFirst(leftNode.left); deque.offerFirst(leftNode.right); deque.offerLast(rightNode.right); deque.offerLast(rightNode.left); } return true; } /** * 迭代法 * 使用普通队列 */ public boolean isSymmetric3(TreeNode root) { Queue<TreeNode> deque = new LinkedList<>(); deque.offer(root.left); deque.offer(root.right); while (!deque.isEmpty()) { TreeNode leftNode = deque.poll(); TreeNode rightNode = deque.poll(); if (leftNode == null && rightNode == null) { continue; } // if (leftNode == null && rightNode != null) { // return false; // } // if (leftNode != null && rightNode == null) { // return false; // } // if (leftNode.val != rightNode.val) { // return false; // } // 以上三个判断条件合并 if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) { return false; } // 这里顺序与使用Deque不同 deque.offer(leftNode.left); deque.offer(rightNode.right); deque.offer(leftNode.right); deque.offer(rightNode.left); } return true; } 104.二叉树的最大深度
题目描述
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
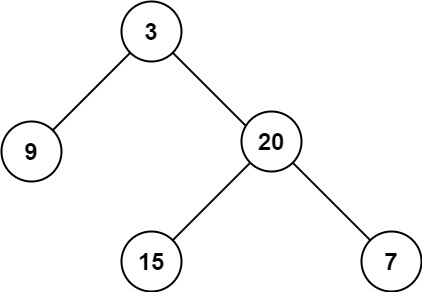
输入:root = [3,9,20,null,null,15,7] 输出:3 示例 2:
输入:root = [1,null,2] 输出:2 提示:
- 树中节点的数量在
[0, 104]区间内。 -100 <= Node.val <= 100
参考代码
class solution { /** * 递归法 */ public int maxDepth(TreeNode root) { if (root == null) { return 0; } int leftDepth = maxDepth(root.left); int rightDepth = maxDepth(root.right); return Math.max(leftDepth, rightDepth) + 1; } } 111.二叉树的最小深度
题目描述
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
示例 1:
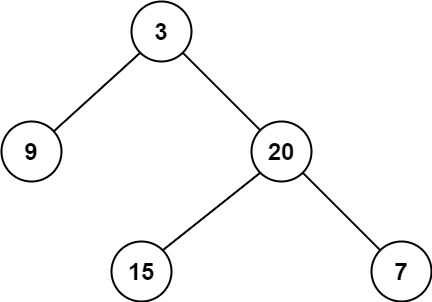
输入:root = [3,9,20,null,null,15,7] 输出:2 示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5 提示:
- 树中节点数的范围在
[0, 105]内 -1000 <= Node.val <= 1000
参考代码
class Solution { /** * 递归法,相比求MaxDepth要复杂点 * 因为最小深度是从根节点到最近**叶子节点**的最短路径上的节点数量 */ public int minDepth(TreeNode root) { if (root == null) { return 0; } int leftDepth = minDepth(root.left); int rightDepth = minDepth(root.right); if (root.left == null) { return rightDepth + 1; } if (root.right == null) { return leftDepth + 1; } // 左右结点都不为null return Math.min(leftDepth, rightDepth) + 1; } } 