基于GARCH-Copula-CVaR模型的金融系统性风险溢出效应matlab模拟仿真

目录

1.程序功能描述

2.测试软件版本以及运行结果展示

3.核心程序

4.本算法原理

5.完整程序

1.程序功能描述

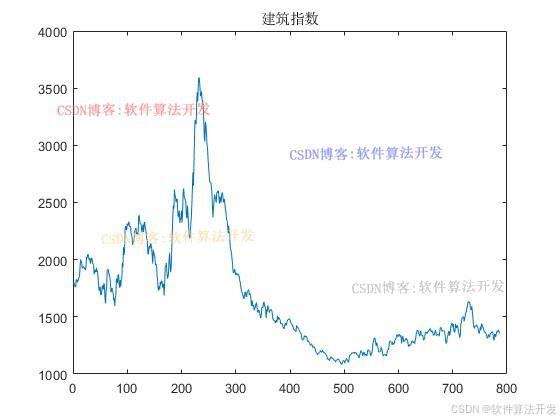
       基于GARCH-Copula-CVaR模型的金融系统性风险溢出效应matlab模拟仿真，仿真输出计算违约点，资产价值波动率，信用溢价，信用溢价直方图等指标。

2.测试软件版本以及运行结果展示

MATLAB2022A版本运行

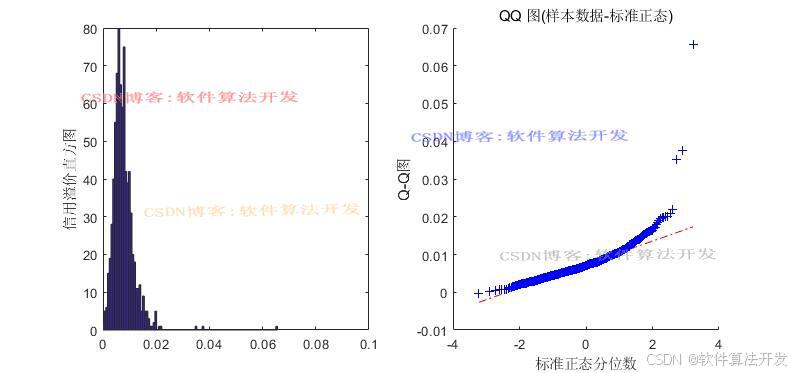
（完整程序运行后无水印）

3.核心程序

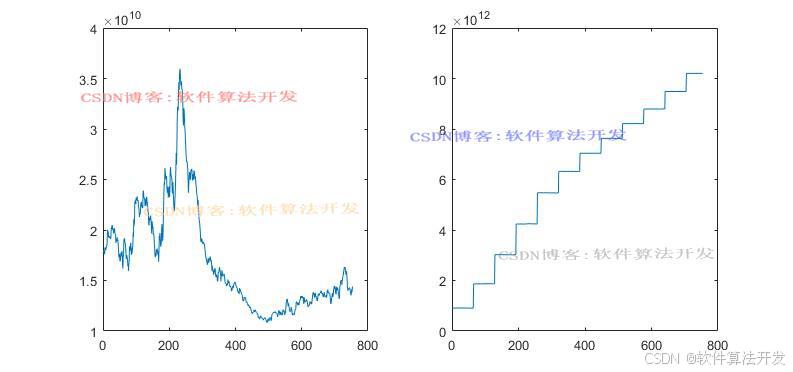
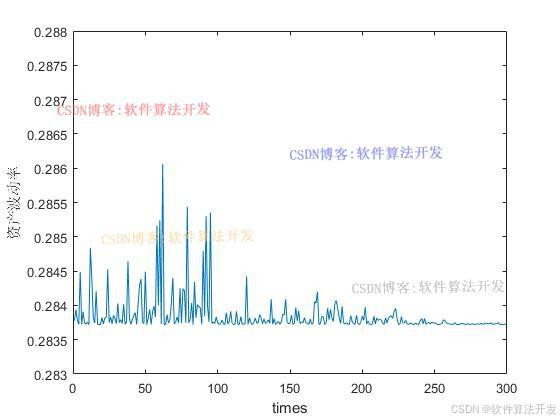
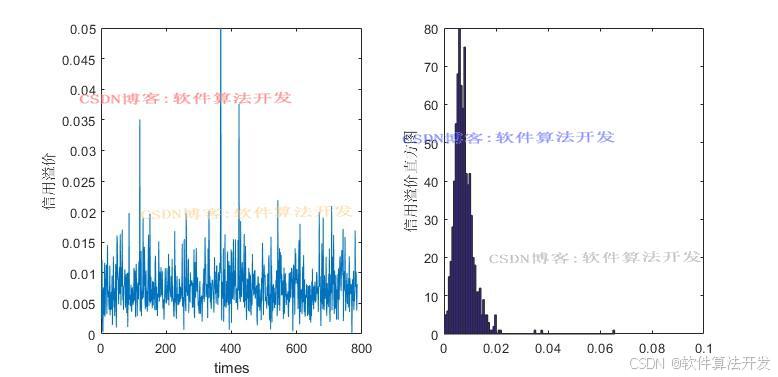
.......................................................... %计算违约点 DP = SD+k*LD;  figure; subplot(121); plot(SD(1:end-NN/2)); subplot(122); plot(DP(1:end-NN/2));   %% %资产价值波动率-图2 R    = func_Rsy(dat1); zeta = func_GARCH(R); figure; plot(zeta); xlabel('times'); ylabel('资产波动率'); axis([0,300,0.283,0.288]);   %% %信用溢价和表2数据分析 [Rc,d] = func_xyyj(dat1,zeta,DP);  figure; subplot(121); plot(Rc); xlabel('times'); ylabel('信用溢价'); axis([0,800,0.0,0.05]);  subplot(122); hist(Rc,100); axis([0,0.1,0.0,80]);  ylabel('信用溢价直方图'); d(1:7)' d(8)'   %% %信用风险部分的参数估计表3的结果 beta_mean = mean(Rc); %求均值 beta_std = std(Rc);   %求标准差 a = (((1-beta_mean)*(beta_mean.^2))/(beta_std.^2) - beta_mean);  b = ((1-beta_mean)/beta_mean)*a;    disp('a值'); a  disp('b值'); b  %自信区间 [a-1.96*beta_std*a,a+1.96*beta_std*a]  [b-1.96*beta_std*b,b+1.96*beta_std*b]     %% %QQ图 figure; subplot(121); hist(Rc,100); axis([0,0.1,0.0,80]);  ylabel('信用溢价直方图'); subplot(122); qqplot(Rc); ylabel('Q-Q图');  %% %Var Cvar  [VaR1,CVaR1]=var_cvar(Rc,0.95);  [VaR2,CVaR2]=var_cvar(Rc,0.99);   disp('历史模拟'); disp('    0.95                0.99'); [VaR1,CVaR1,VaR2,CVaR2]   [VaR1,CVaR1]=var_cvar_mtkl(Rc,0.95);  [VaR2,CVaR2]=var_cvar_mtkl(Rc,0.99);   disp('蒙特卡洛模拟'); disp('    0.95                0.99'); [VaR1,CVaR1,VaR2,CVaR2] 16_043m

4.本算法原理

        GARCH-Copula-CVaR模型是一种复杂的风险度量框架，广泛应用于金融市场，特别是用于分析和量化系统性风险的溢出效应。该模型结合了三个重要的理论框架：广义自回归条件异方差模型（Generalized Autoregressive Conditional Heteroskedasticity, GARCH）、Copula理论以及条件价值风险（Conditional Value at Risk, CVaR）。

       GARCH模型主要用于描述和预测资产收益序列的波动性。基本的GARCH(p,q)模型表述为：

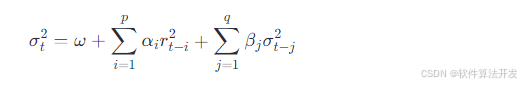
其中，σt2​表示在时间t上的条件波动率；ω是常数项；αi​和βj​分别是过去收益率平方项和过去波动率项的权重系数；p和q分别为模型的滞后阶数；rt​是资产的日对数收益率。

       Copula是用来描述多个随机变量之间依赖结构的一种强大工具。假设我们有两个资产的边际分布函数分别为F1​(x)和F2​(y)，通过一个合适的Copula函数C(u1​,u2​)，我们可以得到它们的联合分布函数：

        其中，u1​=F1​(x)和u2​=F2​(y)是变量的边际分布的累积分布函数值。常见的Copula函数有高斯Copula、t-Copula、Clayton和Frank Copula等，它们各自捕捉不同类型的依赖结构。

        CVaR，也称为期望尾部损失（Expected Shortfall），是风险度量的一种，它衡量的是在给定的置信水平α下，预期超过VaR（Value at Risk）的损失平均值。对于一个随机变量X，其在置信水平α下的CVaR定义为：

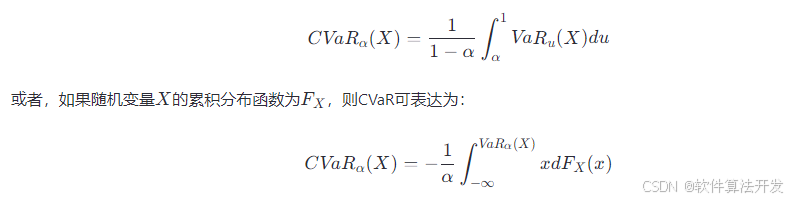
       在GARCH-Copula-CVaR模型中，首先使用GARCH模型估计单个资产的波动性，然后通过Copula方法捕捉资产间的相关性和极端事件的依赖结构，最后应用CVaR来度量整个金融系统的风险溢出效应。

具体步骤如下：

GARCH模型应用：对每个资产的收益率序列分别拟合GARCH模型，得到每个资产的条件波动率序列{σti​}。

Copula联合分布：利用各资产收益率的边际分布函数和选择的Copula函数，构建多资产的联合分布。首先，将每个资产的收益率标准化为标准正态分布（或其他分布），然后通过Copula函数得到联合分布。

系统性风险溢出计算：基于联合分布，计算整个系统在特定置信水平下的CVaR。这一步骤涉及计算所有资产组合的损失分布的上尾部分，反映了极端市场情况下整个系统可能面临的平均损失水平，即系统性风险溢出。

5.完整程序

VVV