论文翻译：通过云计算对联网多智能体系统进行预测控制_业界新闻

发布时间:2024-07-17 19:22

阅读量:9

通过云计算对联网多智能体系统进行预测控制

文章目录

通过云计算对联网多智能体系统进行预测控制
摘要

摘要

本文研究了基于云计算的网络化多智能体预测控制系统的设计与分析。该文提出一种网络化多智能体系统（NMAS）云预测控制方案，以同时实现一致性和稳定性，并主动补偿网络时延。详细介绍了NMAS云预测控制器的设计。对云预测控制方案的分析给出了闭环网络化多智能体控制系统稳定性和一致性的必要和充分条件。通过仿真验证了所提方案表征NMAS的动力学行为和控制性能。研究结果为NMAS及其应用的合作和协调控制的发展奠定了基础。

论文链接：Predictive Control of Networked Multiagent Systems via Cloud Computing | IEEE Journals & Magazine | IEEE Xplore

期刊：IEEE Transactions on Cybernetics

分区：Q1

论文引用：G. -P. Liu, “Predictive Control of Networked Multiagent Systems via Cloud Computing,” in IEEE Transactions on Cybernetics, vol. 47, no. 8, pp. 1852-1859, Aug. 2017, doi: 10.1109/TCYB.2017.2647820.

前言

多智能体系统（MAS）是一组相互通信的智能体，其中每个智能体都是抽象实体或物理实体。近年来，通信技术，特别是互联网技术的进一步发展，导致一些MAS利用通信网络相互交换信息。这导致了一个名为联网MAS（NMAS）的新系统。该系统通常由许多通过网络交互的简单智能体/子系统组成。最重要的NMAS应用是物联网（IoT）[1]，它是全球经济中最热门的增长部门之一。

各种NMAS广泛应用于科学和工程领域，如智能电网，卫星通信，GPS，机器人网络，生物网络，传感器网络，无人驾驶车辆，电力系统等。[2]–[5]。NMAS 中的每个智能体在执行特定操作时都有自己的分布式知识、功能或技能。但是，尽管存在常见的松散耦合网络拓扑，但隔离智能体单独执行操作是不寻常的，甚至是无用的。NMAS中的所有智能体都应位于类似的环境中，并且它们可以通过一系列交互协议进行通信。因此，NMAS可用于对许多现有的复杂系统进行建模，其相应的研究可以为我们带来新的方法来处理任何单个智能体无法解决的问题。至于NMAS技术使用的相关优势，与目前其他可用方法相比，有很多优点，例如可靠性，灵活性，鲁棒性，可重用性，可扩展性，可维护性等。

NMAS合成涉及通过智能体之间的局部交互协议生成所需的集体行为。NMAS的主要研究可分为两个方向：1）传感器网络分布式估计技术的发展和2）使用通过网络获得的信息控制移动自主智能体。在过去的几年里，对这两个方向都作出了各种重要贡献。更具体地说，已经通过采用从控制系统理论到图论的方法研究了移动机器人编队的控制策略，并且在[6]中介绍了机器人在编队中可以具有的许多可能转换。基于虚拟结构方法，解决了多航天器的编队控制思路[7]。已经研究了一组在具有可测量向量场的空间中动态进化的自主智能体的编队控制和同时跟踪，所提出的方法可以通过合作控制它们的轨迹来保证能够实现和维持智能体所需的形成[8]。基于尺度理论和分布式线性迭代的算法，提出了一种实现任意维相对感知网络的简单分布式算法，并分析了其收敛特性[9]。提出了一种在有向图上对MAS进行分布式协同最优控制的逆最优方法[10]。解决了具有活动领导者和可变互连拓扑的多智能体的一致性控制问题，并且为每个自治智能体给出了基于邻居的本地控制器和基于邻居的状态估计规则，以便遵循这样的领导者[11]。提出了一种具有可变时延和切换拓扑结构的连续时间MAS异步一致性策略，并提供了一种有效的分布式一致性算法来克服不可靠的通信信道造成的困难[12]。

NMAS分析研究网络架构和网络组件之间的交互如何影响全球目标。NMAS的关键问题是一致性问题，需要与所有智能体商达成协议。这意味着分布式控制策略需要使用本地信息进行设计，以便所有智能体就某些数量的兴趣达成所需的协议。这个话题已经在工程和科学的各个领域得到了解决，并且在一致性问题上取得了许多有趣的结果。NMAS的一致性能力通常与每个智能体的隔离动力学及其连接拓扑结构有关。一旦确定了隔离的智能体动态，NMAS的一致性能力取决于其连接拓扑结构。在NMAS中，已经见证了各种开创性的贡献涉及不同的分布式策略达成一致性。具有和没有网络延迟的通信网络的一致性标准已经引入，并针对具有固定和交换拓扑的MAS进行收敛分析[13]，[14]。已经讨论了具有网络延迟的非定向NMAS的平均一致性问题，并在有界网络延迟下推导出了其存在的充分条件[15]。[16]中解决了具有时变延迟的MAS的渐近平均一致性问题，[17]中已经考虑了具有随机网络延迟的二阶马尔可夫跳跃MAS的一致性问题。复杂动态网络（CDN）通常由大量互连的动态节点组成，最近引起了极大的关注[18]。由于通信连接拓扑在形成 CDN 行为中起着至关重要的作用，因此已经研究了各种连接拓扑，以了解网络的通信拓扑如何影响网络的行为。CND的同步是影响网络行为的最重要问题之一，并且已经对具有不同节点的CDN进行了广泛的研究[19]。CDN同步问题的思想和结果已应用于NMAS的一致性问题[20]。

这篇关于NMAS的论文基于其计算效率和速度，极大地降低了系统的建立，运行和维护费用。然而，NMAS的研究仍然面临许多挑战和困难，特别是在设计和分析方面。例如，如何制定或分解相关任务和目标;如何设计高效有效的控制协议来补偿通信约束;如何保证稳定性，同时达成一致性。这些问题需要解决，以便NMAS的广泛应用，特别是物联网。针对上述挑战和难点，本文考虑了两个目标：1）NMAS的稳定性和一致性，提出了主动高效地补偿通信时延的云预测控制方案;2）推导出闭环NMAS稳定性和一致性的必要和充分条件。此外，仿真还利用所提出的云预测控制方案说明了NMAS的动态行为和控制性能。

通过云计算实现联网的多智能体控制系统

在 NMAS 中，存在多个控制器而不是单个控制器，并且智能体之间存在各个智能体控制器必须考虑的交互。每个单独的智能体控制器都采用一种控制策略，例如网络预测控制（NPC）[21]。它现在不仅考虑动态和目标，还考虑沟通限制。每个智能体控制器根据自己的信息解决控制问题，并与其他智能体控制器共享信息，以提高整体性能。在NMAS中，随着系统规模的增加，捕获的实时数据和所需的实时计算将急剧增长。存在许多挑战，包括数据的捕获、存储、可视化、共享、传输、搜索和分析，以及计算任务的分配和协调。使用传统的数据库管理和处理工具很难处理这种实时大数据和计算。

随着网络技术和计算技术的发展，云计算已经走进了我们的日常生活。现在，云计算已经超越了它最初的产品概念，成为一种服务。它提供了一个动态可扩展和虚拟化资源的共享池，包括数据访问、计算、软件和存储服务。云控制系统的概念在[22]和[23]中作为网络控制系统的延伸进行了简要讨论，表明云控制系统的研究将在不久的将来对控制系统理论和实际应用做出新的贡献。本文将云计算和预测控制以通用形式引入网络化多智能体控制系统，以克服传统NMAS中存在的实时大数据、通信时延、重计算和多任务协调等难题。针对云计算的优点，该文提出一种基于云的NMAS控制策略。通过云计算的网络化多智能体控制系统的架构如图1所示。

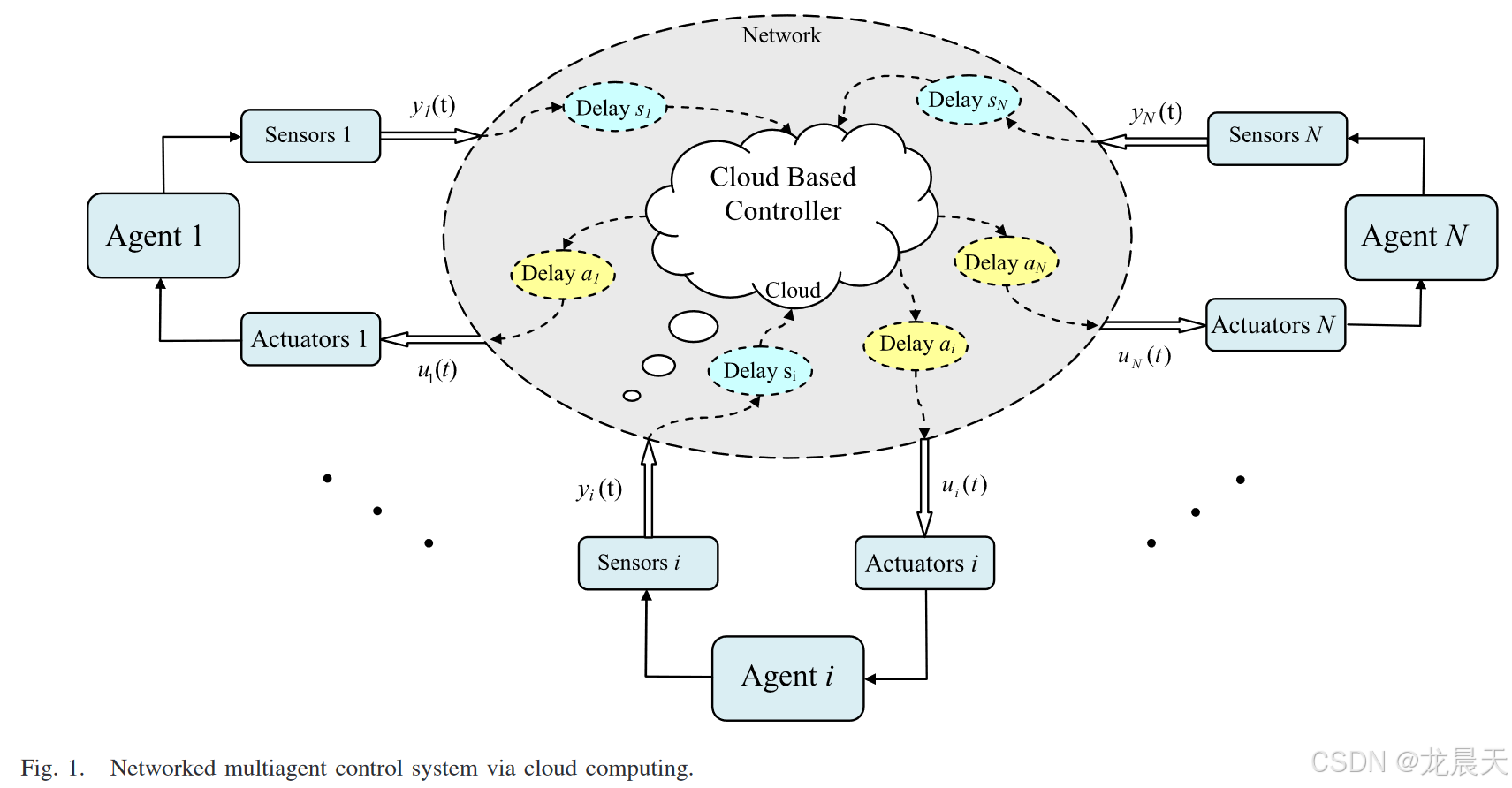
采用云化控制策略，通过云计算实现NMAS控制方法。传感器捕获的NMAS实时数据将通过网络发送到云计算系统，数据按照网络化控制方法处理后，将生成控制序列并通过网络发送回各个智能体的执行器。每个智能体通过网络链接到云计算系统中的控制器云节点。所有控制器云节点在云计算系统中链接并交换信息。每个控制器云节点都具有任务管理、数据收集和计算功能，并在其域上以一定的频率持续广播请求，以便其覆盖域中的所有非控制器云节点都能接收到该请求。在每个采样周期内，会选择一些合适的非控制器云节点来执行控制器云节点分配的各种子任务（如状态估计、参数优化、智能体配合、控制预测等），并将结果返回给控制器云节点。这样，基于云的控制策略将为NMAS的控制提供强大的工具，这是以前无法想象的。

由于 NMAS 中的所有智能体都通过网络与云计算系统通信，因此存在影响 NMAS 建模和设计的通信约束。关键的通信约束是网络延迟、数据丢失和数据安全。它们严重影响NMAS的控制性能。网络延迟是第i个智能体的传感器与云计算系统之间的延迟 $s_i$ ，以及第i个智能体的执行器与云计算系统之间的延迟 $a_i，∀i∈N$ ，其中 $N = {1, 2, .. .,N}$ 和 $a_i$ 和 $s_i$ 是整数。下一节将考虑对网络延迟的补偿。数据丢失和数据安全可以分别通过 [21] 和 [24] 中使用的策略来处理。

网络化多智能体系统的云预测控制器设计

无论网络类型如何，NMAS 的性能始终受到通信约束的影响。众所周知，这些约束会降低网络系统的性能。因此，为了处理闭环NMAS中的通信约束，需要一种先进的控制方法。为了应对这些限制，需要开发一种新的网络控制结构。通信网络的主要特征之一是它们每次都可以传输一个数据包，而不是单个数据，这在非网络控制系统中无法完成。充分利用这一网络特性，引入NMAS的NPC策略[21]，克服随机网络延迟和数据丢失的影响。该策略将由控制预测生成器和网络约束补偿器组成。控制预测生成器基于动态模型和要优化的性能函数，将使用可用信息生成控制预测序列t ，其中包含多个提前一步控制预测t 向前。该控制预测序列将被打包在一起，并通过网络传输到受控智能体端。受控智能体侧的网络约束补偿器将为时间选择最新的控制预测t 从所有可用的控制预测序列中就通信约束的类型而言，并将其应用于受控智能体的执行器。通过这种方式，通信约束，特别是网络时延和数据丢失将得到积极补偿，NPC策略将提供与NMAS相同或渐近相同的控制性能，而没有通信约束。

为简化表述，做出以下假设：

云控制器与第 $i$ 个智能体传感器之间存在网络延迟 $s_i$ ，云控制器与第 i 个智能体执行器之间存在网络延迟 $a_i$ ；
云计算系统中节点间的网络时延远小于联网时延，忽略不计；

网络延迟 $s_i$ 和 $a_i$ 是已知整数，是智能体采样率的倍数。

为了说明如何轻松地设计、分析和执行云预测控制方案，下面考虑了线性非同一多智能体。实际上，该方案可以扩展到更一般的 NMAS，例如具有不确定性和干扰的非线性 NMAS
$\begin{align} x_{i} (t+1)=&A_{i} x_{i} (t)+B_{i} u_{i} (t) \notag \\ y_{i} (t)=&C_{i} x_{i} (t) \end{align}$
∀i ∈ N，其中 $x_i∈R^{n_i}$ ， $y_i∈l$ ， $u_i∈m_i$ 分别是第 $i$ 个智能体的状态、输出和输入向量， $A_i∈R^{n_i×n_i}$ ， $B_i ∈R^{n_i×m_i}$ ， $C_i ∈R^{l×n_i}$ 是第 i 个智能体的矩阵。

假设所有智能体都是可观察的，但它们的状态是不可测量的。然后，基于输出 $y_i(t − s_i)$ 和控制输入 $u_i(t − s_i)$ ，第 i 个智能体的状态观察器设计如下：
$\begin{align} \hat {x}_{i} \left ({t-s_{i} +1 | t-s_{i} }\right )=&A_{i} \hat {x}_{i} \left ({t-s_{i} | t-s_{i} -1}\right )+B_{i} u_{i} \left ({t-s_{i} }\right )\notag \\&+ \,\, F_{i} \left ({y_{i} \left ({t-s_{i} }\right )-\hat {y}_{i} \left ({t-s_{i} | t-s_{i} -1}\right )}\right ) \notag \\ \hat {y}_{i} \left ({t-s_{i} | t-s_{i} -1}\right )=&C_{i} \hat {x}_{i} \left ({t-s_{i} | t-s_{i} -1}\right ) \end{align}$
其中 $\hat {x}_{i} (t-k|t-j)\in \Re ^{n_{i}} (k<j)$ 表示第 i 个智能体根据时间 $t - j$ 之前的可用信息对时间 $t - k$ 的状态预测， $\hat {y}_{i} (.|.)\in \Re ^{l_{i}}$ 是输出预测， $F_{i} \in \Re ^{n_{i} \times l_{i}}$ 是观察者增益矩阵。

要使用直到时间 $t − s_i$ 的可用信息来预测第 i 个智能体的状态，可以使用从 $t − s_i + 2$ 到 $t + a_i$ 开始的以下时间状态估计：
$\begin{align} \hat {x}_{i} \left ({t-s_{i} +k | t-s_{i} }\right )=&A_{i} \hat {x}_{i} \left ({t-s_{i} +k-1 | t-s_{i} }\right )\notag \\&+ \,\, B_{i} u_{i} \left ({t-s_{i} +k-1}\right ) \\ \hat {y}_{i} \left ({t-s_{i} +k | t-s_{i} }\right )=&C_{i} \hat {x}_{i} \left ({t-s_{i} +k | t-s_{i} }\right ) \end{align}$
假设所需的参考输入由阶跃信号向量 $r_0$ 表示，并且仅应用于其中一个智能体，例如，具有 $a_1 ≥ a_i，∀i ∈ N − {1}$ 的第一个智能体。为了跟踪这个所需的参考输入，引入了一组动态变量
$\begin{align} z_{1} \left ({t+1+a_{1}}\right )=&z_{1} \left ({t+a_{1}}\right )+\hat {y}_{1} \left ({t+a_{1} | t-s_{1} }\right )-r_{0}\qquad \\ z_{i} \left ({t+1+a_{i} }\right )=&z_{i} \left ({t+a_{i}}\right )+\hat {y}_{i} \left ({t +a_{i} | t-s_{i} }\right )\notag \\&- \,\, \hat {y}_{1} \left ({t +a_{i} | t- s_{1} }\right ). \end{align}$
(5)和(6)中动态变量的作用相当于常规控制系统中的积分作用，可以消除稳态跟踪误差。为了主动补偿网络延迟 $s_i$ 和 $a_i，∀i ∈ N$ ，NMAS 的预测控制协议如下：
$\begin{align} \hat {u}_{i} \left ({t+a_{i} | t-s_{i} }\right )=&G_{i} z_{i} \left ({t+a_{i} }\right )\notag \\&+ \,\, H_{i} \sum _{j=1}^{N}c_{ij} \Biggl ({\hat {y}_{j} \left ({t+a_{i} | t-s_{j} }\right )}\notag \\&\qquad \qquad \qquad {- \,\, \hat {y}_{i} \left ({t+a_{i} | t-s_{i} }\right )}\Biggr )\qquad \end{align}$
其中
$\begin{equation} c_{ij} =\begin{cases} {1}, & {\mathrm{ if}}~a_{i} \, \le \, a_{j}\\ {0},& {\mathrm{ if}}~a_{i} \, >a_{j}. \end{cases} \end{equation}$
$G_i ∈R^{m_i×m_i}$ 和 $H_i ∈R^{m_i×l_i}$ 是需要设计的增益矩阵。以上暗示预测控制协议利用基于时间 $t − s_i,∀i ∈ N$ 可用信息的输出预测来估计时间 $t + a_i,∀i ∈ N$ 的未来控制行为。实际上，所提出的预测控制协议由两部分组成。一个是让智能体 1 跟踪所需的参考，让其他智能体跟踪智能体 1 的输出，这由 (7) 中右侧的第一项表示。另一个是智能体之间的协调，由（7）中右侧的第二项表示。

然后，第 i 个智能体的预测控制输入被设计为
$\begin{equation} u_{i} \left ({t+a_{i}}\right )=\hat {u}_{i} \left ({t+a_{i} | t-s_{i}}\right ). \end{equation}$
因此，第 i 个智能体的控制输入为
$\begin{equation} u_{i} (t)=\hat {u}_{i} \left ({t | t-s_{i} -a_{i}}\right ). \end{equation}$

因此，云预测控制方案被提出如下。

来自传感器的所有智能体的输出数据 $y_i(t),∀i ∈ N$ , 在每个采样时间 t 被发送到网络。

基于从网络接收到的输出数据 $y_i(t − s_i),∀i ∈ N$ ，云计算系统计算预测 $\hat {x}_{i} (t+a_{i} |t-s_{i} ),~\hat {y}_{i} (t+a_{i} |t-s_{i} ),~\hat {u}_{i} (t+a_{i} |t-s_{i} ),~\forall i\in {\mathbb N},$ , 分别使用（3），（4）和（7）的智能体的状态，输出和控制输入，和动态变量 $z_{i}(t+a_{i})$ , $\forall i \in N$ 使用 (5) 和 (6)。
由(9)给出的控制输入预测 $u_{i} (t+a_{i}),∀i ∈ N$ 通过网络从云计算系统发送到每个智能体的执行器。
所有智能体的执行器在每个采样时间 t 从网络接收由 (10) 给出的控制输入 $u_i(t), ∀i ∈ N$ 。

NMAS 的云预测控制方案如图 2 所示。它显示了云预测控制器如何根据智能体输出 $y_i(t − s_i),∀i ∈ N$ 通过云计算系统计算后生成智能体控制输入 $u_{i}(t+a_{i})$ $, \forall i \in N$ 。

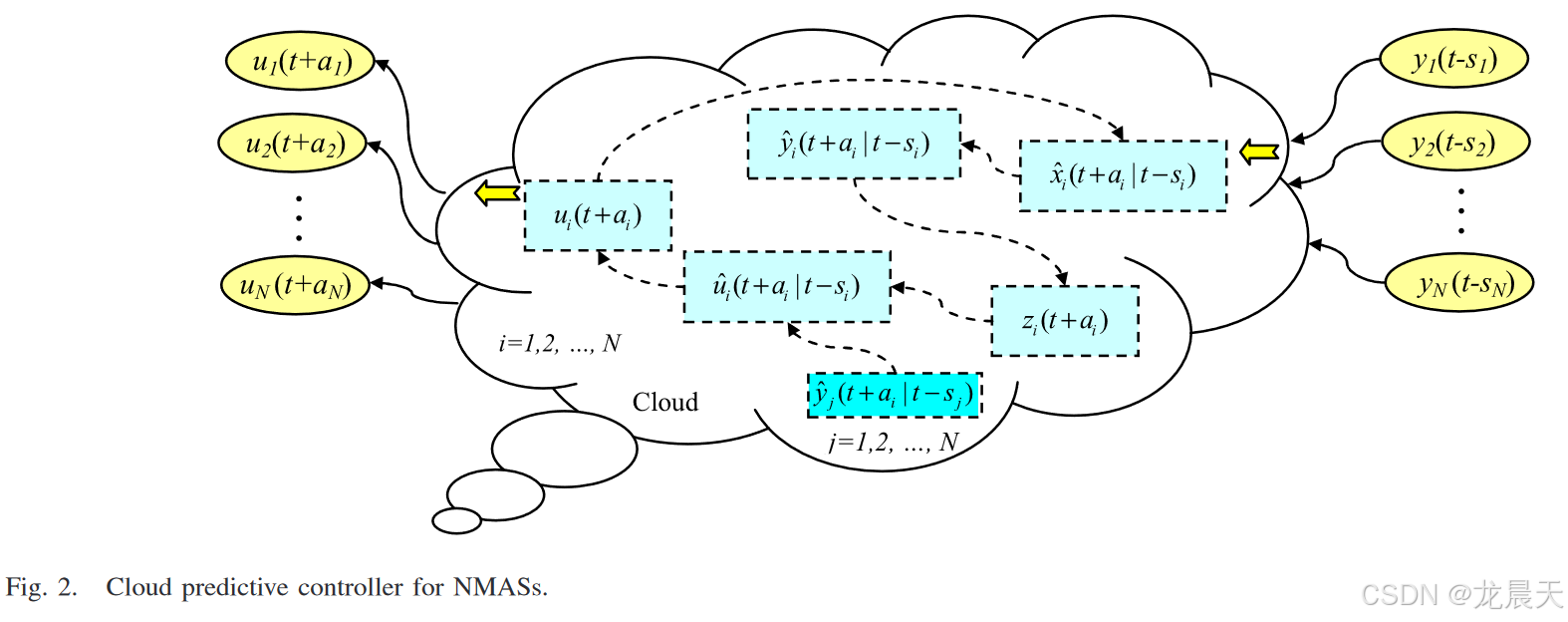
云预测控制系统的稳定性和一致性分析

在实践中，多智能体控制系统不仅需要考虑一致性，还需要考虑稳定性。一致性和稳定性都是多智能体控制系统中非常重要的问题。但目前多智能体控制系统的研究工作往往忽略稳定性问题。在这里，同时分析了具有云预测控制方案的闭环 NMAS 的一致性和稳定性。

定义 1：如果满足以下条件，具有云预测控制方案的 NMAS (1) 输入输出稳定并实现输出一致：

$\lim _{t \to \infty }\left |{ y_{i}(t)-y_{j}(t)}\right |=0, \forall i,j \in \Pi$
$\lim _{t \to \infty }\left |{ y_{i}(t)}\right | < \infty$ ,对于 $t \geq 0$ , $r (·) = r_0$ , 其中 0 取常数， $r_0| < ∞$ .

定义 1 中的条件 1) 意味着所有智能体都实现了输出一致性，条件 2) 意味着每个个体智能体都是输入输出稳定的。

在观察者中将 t 向前移动 $s_i$ 步 (2) 给出
$\begin{align} \hat {x}_{i} \left ({t+1 | t}\right )=&A_{i} \hat {x}_{i} \left ({t | t-1}\right )+B_{i} u_{i} (t)+F_{i} \left ({y_{i} (t) -\hat {y}_{i} \left ({t | t-1}\right )}\right ) \notag \\ \hat {y}_{i} \left ({t | t-1}\right )=&C_{i} \hat {x}_{i} \left ({t | t-1}\right ). \end{align}$
将状态估计误差定义为 $e_{i} (t) =x_{i} (t) -\hat {x}_{i} (t | t-1)$ 。由（1）和（11）可得下列等式：
$\begin{equation} e_{i} (t+1)=\left ({A_{i} -F_{i} C_{i} }\right )e_{i} (t). \end{equation}$
令第 i 个智能体的总网络延迟为 $τ_i = a_i + s_i$ ，第 i 个和第 j 个智能体的混合网络延迟为 $τ_{ij} = a_i + s_j$ 。使用 (3) 递归地计算状态预测导致以下 $τ_i$ 步超前状态预测：
$\begin{align}&\hat {x}_{i} \left ({t+a_{i} | t-s_{i} }\right ) \\[-6pt]&=A_{i}^{\tau _{i} -1} \hat {x}_{i} \left ({t-s_{i} +1 | t-s_{i} }\right ) +\sum _{k=2}^{\tau _{i}}A_{i}^{\tau _{i} -k} B_{i} u_{i} \left ({t+k-s_{i} -1 }\right ) \\&=A_{i}^{\tau _{i} -1} \left ({A_{i} -F_{i} C_{i} }\right )\hat {x}_{i} \left ({t-s_{i} | t-s_{i} -1}\right ) +A_{i}^{\tau _{i} -1} F_{i} C_{i} x_{i} \left ({t-s_{i} }\right ) \\[-2pt]&\quad +\sum _{k=1}^{\tau _{i}}A_{i}^{\tau _{i} -k} B_{i} u_{i} \left ({t+k-s_{i} -1 }\right ) .\qquad ~~ \end{align}$
将上式中的 t 替换为 $t − a_i$ 。然后
$\begin{align} \hat {x}_{i} \left ({t | t-\tau _{i} }\right )=&A_{i}^{\tau _{i} -1} \left ({A_{i} -F_{i} C_{i} }\right )\hat {x}_{i} \left ({t-\tau _{i} | t-\tau _{i} -1}\right )\notag \\&+ \,\, A_{i}^{\tau _{i} -1} F_{i} C_{i} x_{i} \left ({t-\tau _{i} }\right ) \notag \\&+\sum _{k=1}^{\tau _{i}}A_{i}^{\tau _{i} -k} B_{i} u_{i} \left ({t+k-\tau _{i} -1 }\right ) . \end{align}$
递归地使用 (1) 导致
$\begin{equation} x_{i} (t)=A_{i}^{\tau _{i}} x_{i} \left ({ t-\tau _{i} }\right )+\sum _{k=1}^{\tau _{i}}A_{i}^{\tau _{i} -k} B_{i} u_{i} \left ({t+k-\tau _{i} -1 }\right )\qquad \end{equation}$
意思是
$\begin{equation} \sum _{k=1}^{\tau _{i}}A_{i}^{\tau _{i} -k} B_{i} u_{i} \left ({t+k-\tau _{i} -1 }\right ) =x_{i} (t)-A_{i}^{\tau _{i}} x_{i} \left ({ t-\tau _{i} }\right ).\qquad \end{equation}$
将 (14) 右侧的第三项替换为 (16) 产量
$\begin{align} \hat {x}_{i} \left ({t | t-\tau _{i} }\right )=&A_{i}^{\tau _{i} -1} \left ({A_{i} -F_{i} C_{i} }\right )\hat {x}_{i} \left ({t-\tau _{i} | t-\tau _{i} -1}\right ) \notag \\&+ \,\, A_{i}^{\tau _{i} -1} F_{i} C_{i} x_{i} \left ({t-\tau _{i} }\right )+x_{i} (t)-A_{i}^{\tau _{i}} x_{i} \left ({ t-\tau _{i} }\right )\notag \\=&x_{i} (t)+A_{i}^{\tau _{i} -1} \left ({A_{i} -F_{i} C_{i} }\right )\hat {x}_{i} \left ({t-\tau _{i} | t-\tau _{i} -1}\right )\notag \\&- \,\, A_{i}^{\tau _{i} -1} \left ({A_{i} -F_{i} C_{i}}\right )x_{i} \left ({t-\tau _{i}}\right ) \notag \\=&x_{i} (t)-A_{i}^{\tau _{i} -1} \left ({A_{i} -F_{i} C_{i} }\right )e_{i} \left ({ t-\tau _{i} }\right )\notag \\=&x_{i} (t)-A_{i}^{\tau _{i} -1} e_{i} \left ({ t-\tau _{i} +1}\right ) \end{align}$
它使用（12）。采用上述状态预测，云预测控制协议（10）可以重写为
$\begin{align} u_{i} (t)=&\hat {u}_{i} \left ({t | t-\, s_{i} -\, a_{i} }\right )\, =\hat {u}_{i} \left ({t | t-\tau _{i} }\right ) \notag \\[-1pt]=&G_{i} z_{i} (t)+H_{i} \sum _{j=1}^{N}c_{ij} \left ({C_{j} \hat {x}_{j} \left ({t | t-\, \tau _{ij} }\right )-C_{i} \hat {x}_{i} \left ({t | t-\, \tau _{i} }\right )}\right ) \notag \\[-1pt]=&G_{i} z_{i} (t)+H_{i} \sum _{j=1}^{N}c_{ij} \left ({C_{j} x_{j} (t)-C_{i} x_{i} (t)}\right )\notag \\[-1pt]&+ \,\, H_{i} \sum _{j=1}^{N}c_{ij} \Biggl ({C_{i} A_{i}^{\tau _{i} -1} e_{i} \left ({ t-\tau _{i} +1}\right )}\notag \\[-1pt]&\qquad \qquad \qquad {- \,\, C_{j} A_{j}^{\tau _{ij} -1} e_{j} \left ({ t-\tau _{ij} +1}\right )}\Biggr ). \end{align}$
定义 $\Delta x_{i} (t)=x_{i} (t) -x_{i} (t-1)$ 和 $\Delta z_{i} (t)=z_{i} (t) -z_{i} (t-1)$ 。从（1）和（18）可以直接得到第 i 个智能体的以下状态增量：
$\begin{align} \Delta x_{i} (t+1)=&A_{i} \Delta x_{i} (t)\, +B_{i} G_{i} \Delta z_{i} (t) \notag \\[2pt]&+ \,\, B_{i} H_{i} \sum _{j=1}^{N}c_{ij} \left ({C_{j} \Delta x_{j} (t)\, -\, C_{i} \Delta x_{i} (t)}\right )\notag \\[2pt]&+ \,\, B_{i} H_{i} \sum _{j=1}^{N}c_{ij} \Biggl ({C_{i} A_{i}^{\tau _{i} -1} \Delta e_{i} \left ({ t-\tau _{i} +1}\right )}\notag \\[2pt]&\qquad \qquad \qquad {- \,\, C_{j} A_{j}^{\tau _{ij} -1} \Delta e_{j} \left ({ t-\tau _{ij} +1}\right )}\Biggr )\notag \\[2pt]=&\left .{ \left ({A_{i} -B_{i} d_{i} H_{i} }\right )C_{i} }\right )\Delta x_{i} (t)+B_{i} G_{i} \Delta z_{i} (t)\notag \\[2pt]&+ \,\, B_{i} H_{i} \sum _{j=1}^{N}c_{ij} C_{j} \Delta x_{j} (t)\notag \\[2pt]&+ \,\, B_{i} H_{i} \sum _{j=1}^{N}c_{ij} \Biggl ({C_{i} A_{i}^{\tau _{i} -1} \Delta e_{i} \left ({ t-\tau _{i} +1}\right )}\notag \\[2pt]&~\qquad \qquad \quad {-\,C_{j} A_{j}^{\tau _{ij} -1} \Delta e_{j} \left ({ t-\tau _{ij} +1}\right )}\Biggr )\qquad ~ \end{align}$
其中 $d_i = c_{i1} + c_{i2} +···+c_{iN}$ 。因此，NMAS的所有状态增量可以用以下紧凑形式表示：
$\begin{equation} \Delta X(t+1) = \left ({A_{d} -B_{h} +B_{a} }\right )\Delta X(t)+B_{g} \Delta Z(t)+V(t)\qquad ~ \end{equation}$
其中
$\begin{align*} \Delta X(t)=&\left [{\begin{array}{cccc} {\Delta x_{1}^{T} (t)} & {\Delta x_{2}^{T} (t)} & {\cdots } & {\Delta x_{N}^{T} (t)} \end{array}}\right ]^{T}\\[2pt] \Delta Z(t)=&\left [{\begin{array}{cccc} {\Delta z_{1}^{T} (t)} & {\Delta z_{2}^{T} (t)} & {\cdots } & {\Delta z_{N}^{T} (t)} \end{array}}\right ]^{T}\\[2pt] A_{d}=&{\mathrm{ diag}}\left \{{ A_{1} ,\, A_{2} ,\cdots ,\, A_{N} }\right \}\\[2pt] B_{h}=&{\mathrm{ diag}}\left \{{ B_{1} d_{1} H_{1} C_{1} ,\, B_{2} d_{2} H_{2} C_{2} ,\cdots ,B_{N} d_{N} H_{N} C_{N} }\right \}\\[2pt] B_{a}=&\left [{\begin{array}{cccc} {c_{11} B_{1} H_{1} C_{1}} & {c_{12} B_{1} H_{1} C_{2}} & {\cdots } & {c_{1N} B_{1} H_{1} C_{N}} \\[2pt] {c_{21} B_{2} H_{2} C_{1}} & {c_{22} B_{2} H_{2} C_{2}} & {\cdots } & {c_{2N} B_{2} H_{2} C_{N}} \\[2pt] {\vdots } & {\vdots } & {\ddots } & {\vdots } \\[2pt] {c_{N1} B_{N} H_{N} C_{1}} & {c_{N1} B_{N} H_{N} C_{2}} & {\cdots } & {c_{NN} B_{N} H_{N} C_{N}} \end{array}}\right ]\\[2pt] B_{g}=&{\mathrm{ diag}}\left \{{ B_{1} G_{1} ,\, B_{2} G_{2} ,\cdots ,\, B_{N} G_{N} }\right \}\\[2pt] V(t)=&\left [{v_{1}^{T} (t),v_{2}^{T} (t),\cdots ,v_{N}^{T} (t)}\right ]^{T}\\[2pt] v_{i} (t)=&B_{i} H_{i} \sum _{j=1}^{N}c_{ij} C_{j} A_{j}^{\tau _{ij} -1} \left ({e_{j} \left ({ t\, -\, \tau _{ij} }\right )-e_{j} \left ({ t\, -\, \tau _{ij} +1}\right )\, }\right )\\[2pt]&+ \,\, d_{i} B_{i} H_{i} C_{i} A_{i}^{\tau _{i} -1} \Biggl ({e_{i} \left ({ t\, -\, \tau _{i} +1}\right )}\\[2pt]&\qquad \qquad \qquad \qquad \qquad {- \,\, e_{i} \left ({ t\, -\, \tau _{i} }\right )\, }\Biggr ),\forall i\in {\mathbb N}. \end{align*}$
从 (5)、(6) 和 (17) 可以推导出 $z_i(t + 1)$
$\begin{align} \Delta z_{1} (t+1)=&\Delta z_{1} (t)+C_{1} \Delta x_{1} (t)\notag \\&- \,\, C_{1} A_{1}^{\tau _{1} -1} \Delta e_{1} \left ({ t-\tau _{1} +1}\right ) \\ \Delta z_{i} (t+1)=&\Delta z_{i} (t)+\Delta \hat {y}_{i} \left ({t | t-\, \tau _{i} }\right )-\Delta \hat {y}_{1} \left ({t | t-\, \tau _{i1} }\right )\notag \\=&\Delta z_{i} (t)+C_{i} \Delta x_{i} (t)-C_{1} \Delta x_{1} (t)\notag \\&+ \,\, C_{1} A_{1}^{\tau _{i1} -1} \Delta e_{1} \left ({ t-\tau _{i1} +1}\right )\notag \\&- \,\, C_{i} A_{i}^{\tau _{i} -1} \Delta e_{i} \left ({ t-\tau _{i} +1}\right ) \end{align}$
∀i ∈ N −{1}。然后，(21) 和 (22) 的紧凑形式可以描述为 b
$\begin{equation} \Delta Z(t+1) = \left ({\, C_{d} -J_{N} \otimes \, C_{1} }\right )\Delta X(t)\, +\, \Delta Z(t)+W(t)\qquad \end{equation}$
其中
$\begin{align*} C_{d}=&{\mathrm{ diag}}\left \{{ C_{1} ,\, C_{2} ,\cdots ,\, C_{N} }\right \}\\ J_{N}=&\left [{\begin{array}{cc} {\left [{0,1,\cdots ,1}\right ]^{T}} & {0_{n\times (n-1)}} \end{array}}\right ]\\ W(t)=&\left [{w_{1}^{T} (t),w_{2}^{T} (t),\cdots ,w_{N}^{T} (t)}\right ]^{T}\\ w_{1} (t)=&C_{1} A_{1}^{\tau _{1} -1} \left ({e_{1} \left ({ t-\tau _{1} }\right )-e_{1} \left ({ t-\tau _{1} +1}\right )}\right )\\ w_{i} (t)=&C_{1} A_{1}^{\tau _{i1} -1} \left ({e_{1} \left ({ t-\tau _{i1} +1}\right )-e_{1} \left ({ t-\tau _{i1} }\right )}\right )\\&- \,\, C_{i} A_{i}^{\tau _{i} -1} \left ({e_{i} \left ({ t-\tau _{i} +1}\right )-e_{i} \left ({ t-\tau _{i} }\right )}\right ),~\forall i\in {\mathbb N}-\{ 1\} \end{align*}$
⊗ 表示矩阵的克罗内克积。

由(12)可知
$\begin{equation} \varepsilon (t+1)=A_{e} \varepsilon (t)~ \end{equation}$
其中
$\begin{align*} \varepsilon (t)=&\Biggl [{e_{1}^{T} \left ({t-\tau _{1} +1}\right ),e_{1}^{T} \left ({t-\tau _{1} }\right ),e_{2}^{T} \left ({t-\tau _{2} +1}\right ),e_{2}^{T} \left ({t-\tau _{2} }\right ),}\\&\qquad {\cdots ,e_{N}^{T} \left ({t-\tau _{N} }\right )}\Biggr ]^{T}\\ A_{e}=&{\mathrm{ diag}}\Biggl \{{ A_{1} -F_{1} C_{1} ,\, A_{1} -F_{1} C_{1} ,A_{2} -F_{2} C_{2} ,A_{2} -F_{2} C_{2},}\\&\qquad {\cdots ,\, A_{N} -F_{N} C_{N} ,\, A_{N} -F_{N} C_{N} }\Biggr \} . \end{align*}$
因此，结合 (20)、(23) 和 (24)，具有云预测控制方案的闭环 NMAS 可以表示为以下紧凑形式：
$\begin{equation} \left [{\begin{array}{c} {\delta (t+1)} \\ {\varepsilon (t+1)} \end{array}}\right ]=\left [{\begin{array}{cc} {A_{xz}} & {R_{e}} \\ \mathbf {0} & {A_{e}} \end{array}}\right ]\left [{\begin{array}{c} {\delta (t)} \\ {\varepsilon (t)} \end{array}}\right ] \end{equation}$
其中
$\begin{equation} A_{xz} =\left [{\begin{array}{cc} {A_{d} -B_{h} +B_{a}} & {B_{g}} \\ {C_{d} -J_{N} \otimes \, C_{1}} & \mathbf {I} \end{array}}\right ] \end{equation}$
$\delta (t)=[{\Delta X^{T} (t)} \quad {\Delta Z^{T} (t)}]^{T} ,~R_{e} \varepsilon (t)=\, [{V^{T} (t)} \quad {W^{T} (t)}]$

$\delta (t)=[{\Delta X^{T} (t)} \quad {\Delta Z^{T} (t)}]^{T} ,~R_{e} \varepsilon (t)=\, [{V^{T} (t)} \quad {W^{T} (t)}]$

0 和 I 分别表示具有适当维数的零矩阵和单位矩阵。

定理 1：当且仅当所有矩阵 $A_{xz}$ 和 $A_i − F_iC_i, ∀i ∈ N$ , 都是 Schur 稳定时，NMAS (1) 与云预测控制协议 (7) 是稳定的并且达成一致性。

证明：由上可知，采用云预测控制方案的闭环NMAS等价于(25)。这意味着闭环网络化多智能体控制系统稳定的充分必要条件是所有矩阵 $A_{xz}$ 和 $A_e$ 都是Schur稳定的，这意味着矩阵 $A_{xz}$ 和 $A_i-F_iC_i，∀i∈N$ ，是Schur稳定的。

如果系统 (25) 是稳定的，则意味着 $\Delta δ(t) → 0$ 和 $\Deltaε(t) → 0$ ，随着t →∞，这意味着 $x_i(t) → 0，z_i(t) → 0$ 和 $e_i(t) → 0$ 随着 $t \to \infty, \forall i \in N .$

对于 $e_i(t) → 0$ 随着 $t \to \infty$ ，由 (4) 和 (12) 可以得出 $\hat {x}_{i} (t|t-\tau _{i} )\to x_{i} (t)$ 和 $\hat {y}_{i} (t|t-\tau _{i} )\to \hat {y}_{1} (t|t-\tau _{i1} )\to y_{1} (t)$

重写 (5) 和 (6) 可以导致
$\begin{align*} \Delta z_{1} (t+1)=&\hat {y}_{1} \left ({t\, |t-\tau _{1} }\right )-r_{0}\\ \Delta z_{i} (t+1)=&\hat {y}_{i} \left ({t\, |t-\tau _{i} }\right )-\hat {y}_{1} \left ({t | t-\tau _{i1} }\right ),\forall i\in {\mathbb N}-\{ 1\} . \end{align*}$
对于 $\Delta zi(t) → 0ast →∞, ∀i ∈ N,$ 从上面可以看出 $\hat {y}_{1} (t|t-\tau _{1} )\to r_{0}$ , $\hat {y}_{i} (t|t-\tau _{i} )\to y_{i} (t)$

显然，从以上分析可以得出， $y_1(t ) → r_0$ 为 $→∞，y_i(t ) \rightarrow y_1(t)$ 为 $t →∞，∀i ∈ N −{1}$ 。这意味着满足定义 1 的两个条件。

因此，具有云预测控制方案的闭环 NMAS 不仅稳定而且能够达成一致性。注1：上述定理表明，云预测控制方案可以同时实现闭环网络化多智能体控制系统的一致性并保证其稳定性。这是网络多智能体控制系统设计和分析的重大成就。

例子

以具有三个智能体的 MAS 为例来说明 NMAS 的云预测控制方案的性能。三个具有不同动态的智能体的矩阵给出如下：
$\begin{align*} A_{1}=&\left [{\begin{array}{cc} {1.7} & {-1.3} \\ {1.6} & {-1.8} \end{array}}\right ],B_{1} =\left [{\begin{array}{c} {1.0} \\ {2.0} \end{array}}\right ],C_{1} =\left [{\begin{array}{c} {1.0} \\ {0.3} \end{array}}\right ]^{T}\\ A_{2}=&\left [{\begin{array}{cc} {1.8} & {-1.4} \\ {1.8} & {-1.9} \end{array}}\right ],B_{2} =\left [{\begin{array}{c} {1.7} \\ {3.4} \end{array}}\right ],C_{2} =\left [{\begin{array}{c} {0.7} \\ {0.2} \end{array}}\right ]^{T}\\ A_{3}=&\left [{\begin{array}{cc} {1.4} & {-1.1} \\ {1.3} & {-1.5} \end{array}}\right ],B_{3} =\left [{\begin{array}{c} {0.8} \\ {1.6} \end{array}}\right ],C_{3} =\left [{\begin{array}{c} {1.1} \\ {0.4} \end{array}}\right ]^{T} . \end{align*}$
实际上，智能体 1 不稳定，智能体 2 临界稳定，智能体 3 稳定。这三个智能体通过网络由云控制器控制。网络智能体和云计算系统之间的网络延迟设置为a1 = 3，a2 = 2，a3 = 3，s1 = 2，s2 = 4，s3 = 1。可以从（8）中得到c11 = 1，c12 = 0，c13 = 1，c21 = 1，c22 = 1，c23 = 1，c31 = 1，c32 = 0，c33 = 1。在这个例子中，所有智能体状态的初始条件，控制输入和观察者状态为零。第一个智能体所需的参考输入 r0 对于 t ∈ [0, 100) 和 t ∈ [200, 300) 是 1，并且是 0fort ∈ [100, 200)。

控制协议（7）中的增益 $G_i$ 和 $H_i$ 是通过特征结构分配方法[25]设计的，它给出了使矩阵 Axz 稳定的可能解决方案之一，即
$\begin{align*} G_{1}=&-0.16,G_{2} =-0.18,G_{3} =-0.14\\ H_{1}=&-0.12,H_{2} =-0.10,H_{3} =-0.14. \end{align*}$
为了使观察者状态具有良好的收敛速度，观察者的极点应位于理想区域，该区域通常靠近离散时间系统的坐标原点。因此，三个智能体的观察者增益矩阵设计为
$\begin{equation*} F_{1} =\left [{\begin{array}{c} {\mathrm{ -0.4483}} \\ {\mathrm{ -1.1724}} \end{array}}\right ],F_{2} =\left [{\begin{array}{c} {\mathrm{ -0.6803}} \\ {\mathrm{ -1.6191}} \end{array}}\right ],F_{3} =\left [{\begin{array}{c} {\mathrm{ -0.3908}} \\ {\mathrm{ -0.9254}} \end{array}}\right ] \end{equation*}$
使用 MATLAB 中称为“place”的极点放置函数将三个观察者的所需极点分配给 0.3 和 0.4，这为观察者提供了所需的瞬态响应。

本例考虑两种情况。一种是没有网络延迟，另一种是有网络延迟。

情况 1（无网络延迟）：对于这种情况，网络三智能体控制系统中的网络延迟为零（即 $a_i = s_i = 0$ ，对于 i = 1、2、3）和云控制协议(7) 成为
$\begin{equation*} u_{i} (t)= G_{i} z_{i} (t)+H_{i} \sum _{j=1}^{3}c_{ij} \left ({y_{j} (t )-y_{i} (t)}\right ) ,{\mathrm{ for}}~i=1,2,3 \end{equation*}$

$z_{1} (t+1)=z_{1} (t)+y_{1} (t)-r_{0}$ , $z_{i} (t+1)=z_{i} (t)+y_{i} (t)-y_{1} (t ),$

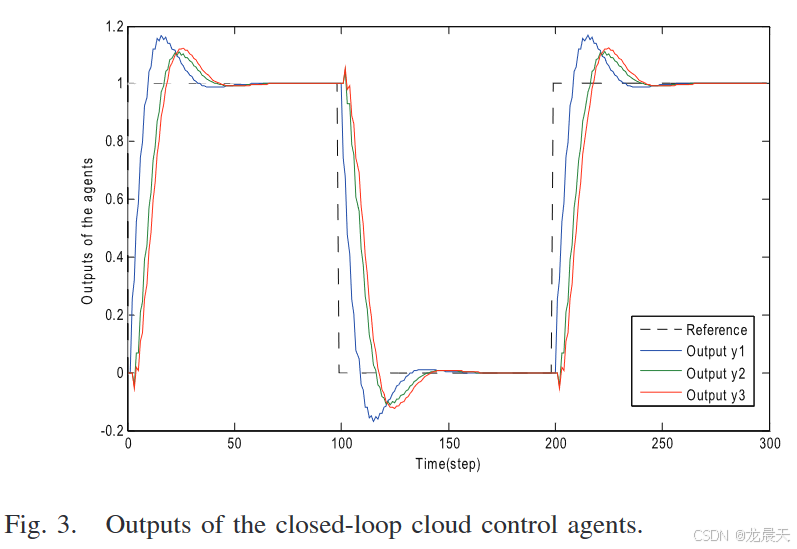
三个闭环云控制智能体的输出 $y_i(t)$ 如图 3 所示。显然，三个智能体是稳定的并且达成一致性非常好。

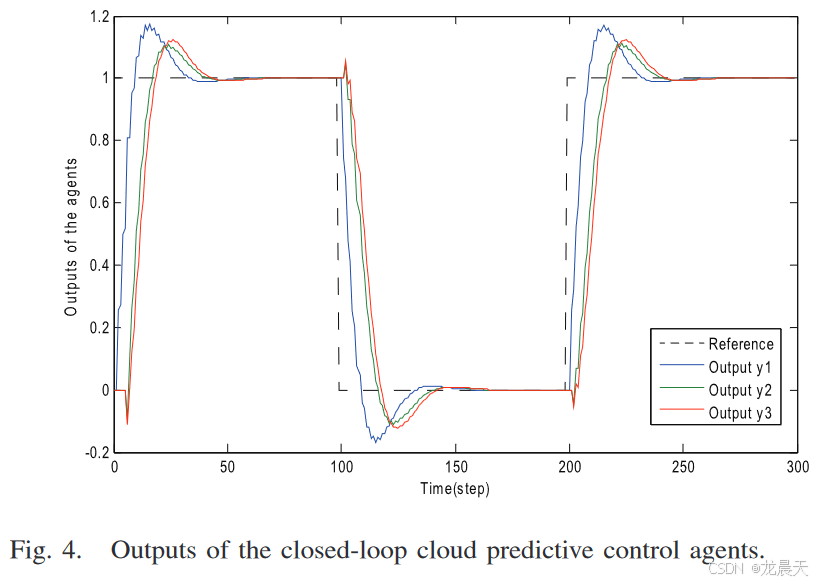
2）案例2（有网络延迟）：对于这种情况，网络三智能体控制系统中存在网络延迟，并且利用云预测控制协议（7），即
$\begin{align*} u_{i} (t)=&G_{i} z_{i} (t)+H_{i} \sum _{j=1}^{3}c_{ij} \Biggl ({\hat {y}_{j} \left ({t | t-a_{i} -s_{j} }\right )}\\&\qquad \qquad \qquad \qquad {- \,\, \hat {y}_{i} \left ({t | t-a_{i} -s_{i} }\right )}\Biggr ),{\mathrm{ for}}~i=1,2,3 \end{align*}$
三个闭环云预测控制智能体的输出 yi(t) 如图 4 所示。从仿真结果可以看出，三个闭环云预测控制智能体的稳定性和一致性性能与案例1之一。

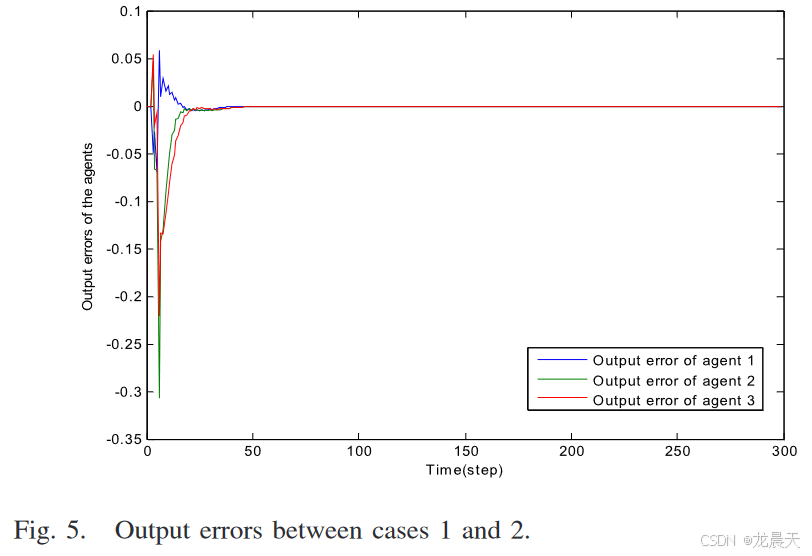
为了精确比较案例 1 和案例 2 的性能，案例 1 和案例 2 之间的输出误差如图 5 所示。很明显，0 ≤ t ≤ 50 存在较大的输出误差，因为状态观察者需要一些时间三个智能体收敛。在这些状态观察器收敛 t > 50 后，情况 1 和 2 之间的输出误差几乎为零。这意味着具有网络延迟的网络多智能体云预测控制系统的性能几乎与没有网络延迟的系统相同。这表明本文提出的云预测控制方案能够很好地主动补偿网络延迟。

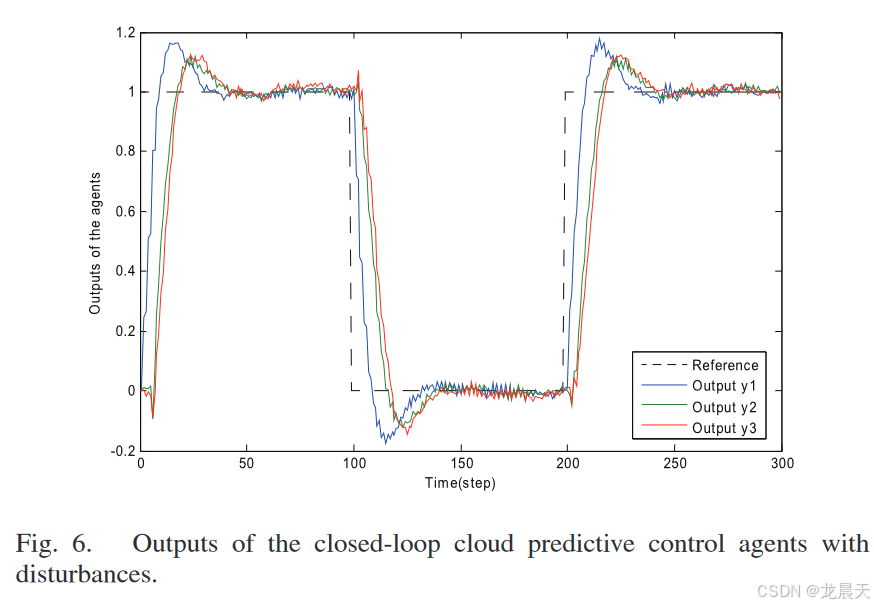
为了说明云预测控制方案的干扰抑制，不同的随机干扰 $d_i(t)∈2x1$ ，对于 i = 1、2、3，在振幅 ±0.005 内被添加到所有个体智能体的状态。这意味着状态方程由 $x_{i} (t+1)=A_{i} x_{i} (t)+B_{i} u_{i} (t)+d_{i} (t)$ ,描述，其中 i = 1、2、3。三个闭环云预测的输出响应控制智能体在图 6 中给出。它表明所提出的云预测控制方案具有干扰抑制能力。

结论

在本文中，提出了一种通过云计算的 NMAS 云预测控制方案，以同时实现一致性和稳定性，并主动补偿通信延迟。研究了网络化多智能体云预测控制系统的设计和分析。它详细介绍了云预测控制架构的外观、如何设计云预测控制器以及如何通过云计算系统实现控制器。导出了闭环网络化多智能体云预测控制系统稳定性和一致性的充分必要条件。一个模拟示例成功地证明了所提出的 NMAS 云预测控制方案的稳定性、一致性和控制性能。云预测控制是一个新思想，以前没有研究过。网络化多智能体云预测控制系统在实践中存在许多潜在的应用，例如智能电网中电力生产和分配的电子功率控制、GPS 卫星编队控制等。虽然本文提供了所提出的云预测控制方案的细节，并且仿真示例演示了它的性能，但它仍处于理论研究阶段，对于一般应用还有很多工作要做。

计和分析。它详细介绍了云预测控制架构的外观、如何设计云预测控制器以及如何通过云计算系统实现控制器。导出了闭环网络化多智能体云预测控制系统稳定性和一致性的充分必要条件。一个模拟示例成功地证明了所提出的 NMAS 云预测控制方案的稳定性、一致性和控制性能。云预测控制是一个新思想，以前没有研究过。网络化多智能体云预测控制系统在实践中存在许多潜在的应用，例如智能电网中电力生产和分配的电子功率控制、GPS 卫星编队控制等。虽然本文提供了所提出的云预测控制方案的细节，并且仿真示例演示了它的性能，但它仍处于理论研究阶段，对于一般应用还有很多工作要做。