【数据结构】初探数据结构面纱：栈和队列全面剖析

avatar
作者
筋斗云
阅读量:1

【数据结构】初探数据结构面纱：栈和队列全面剖析

🔥个人主页：大白的编程日记

🔥专栏：数据结构

文章目录

前言

哈喽，各位小伙伴大家好！今天咱们就正式开始学习数据结构了。我们今天要学习的数据结构分别是栈和队列。话不多说，咱们进入正题！向大厂冲锋！

一.栈

1.1栈的概念及结构

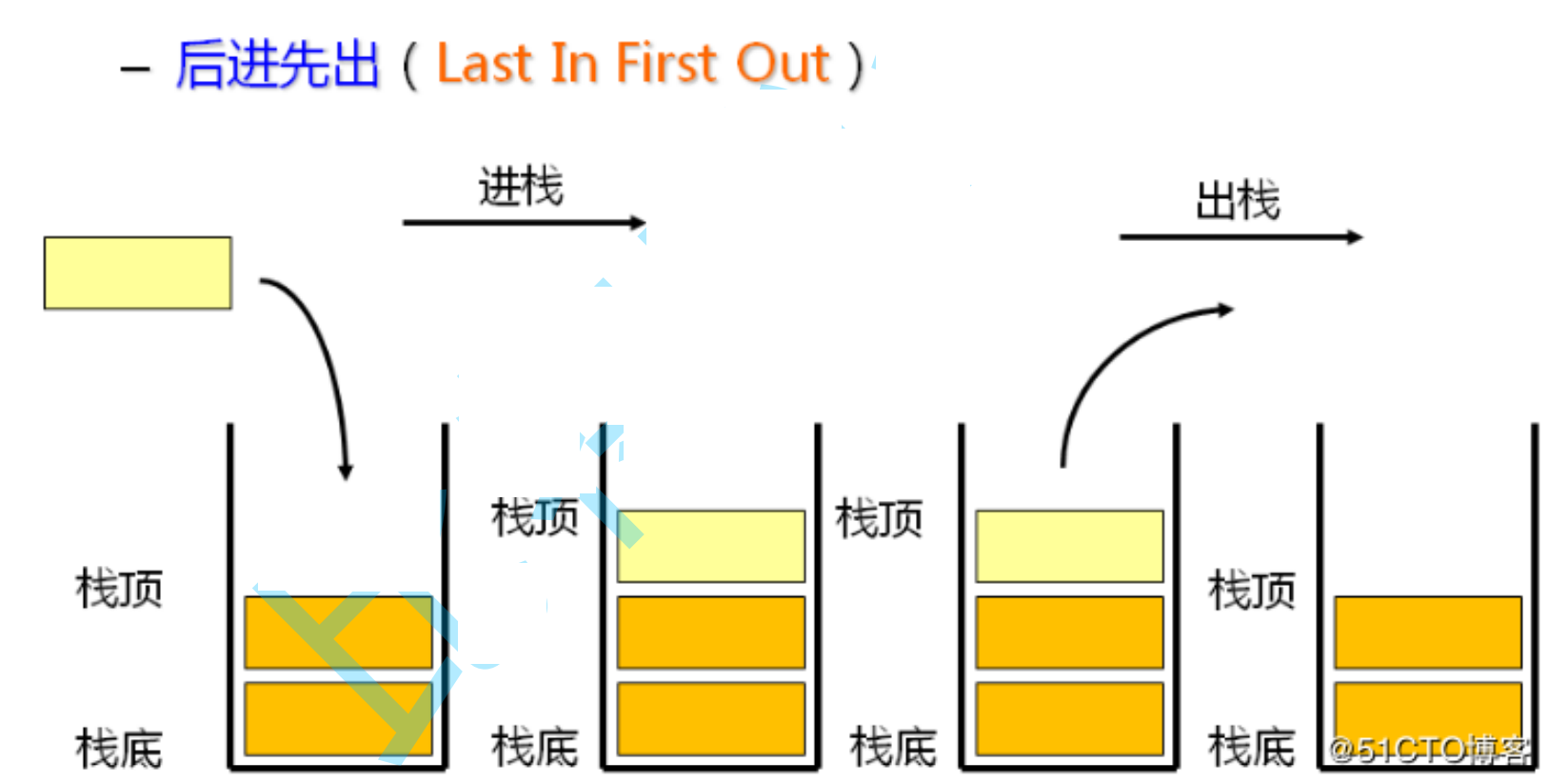
栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

栈是一种遵循后进先出的结构。类似生活中我们生活中的弹夹，羽毛球桶等等。

在这里插入图片描述

  • 入栈
    入栈就是往栈顶增添数据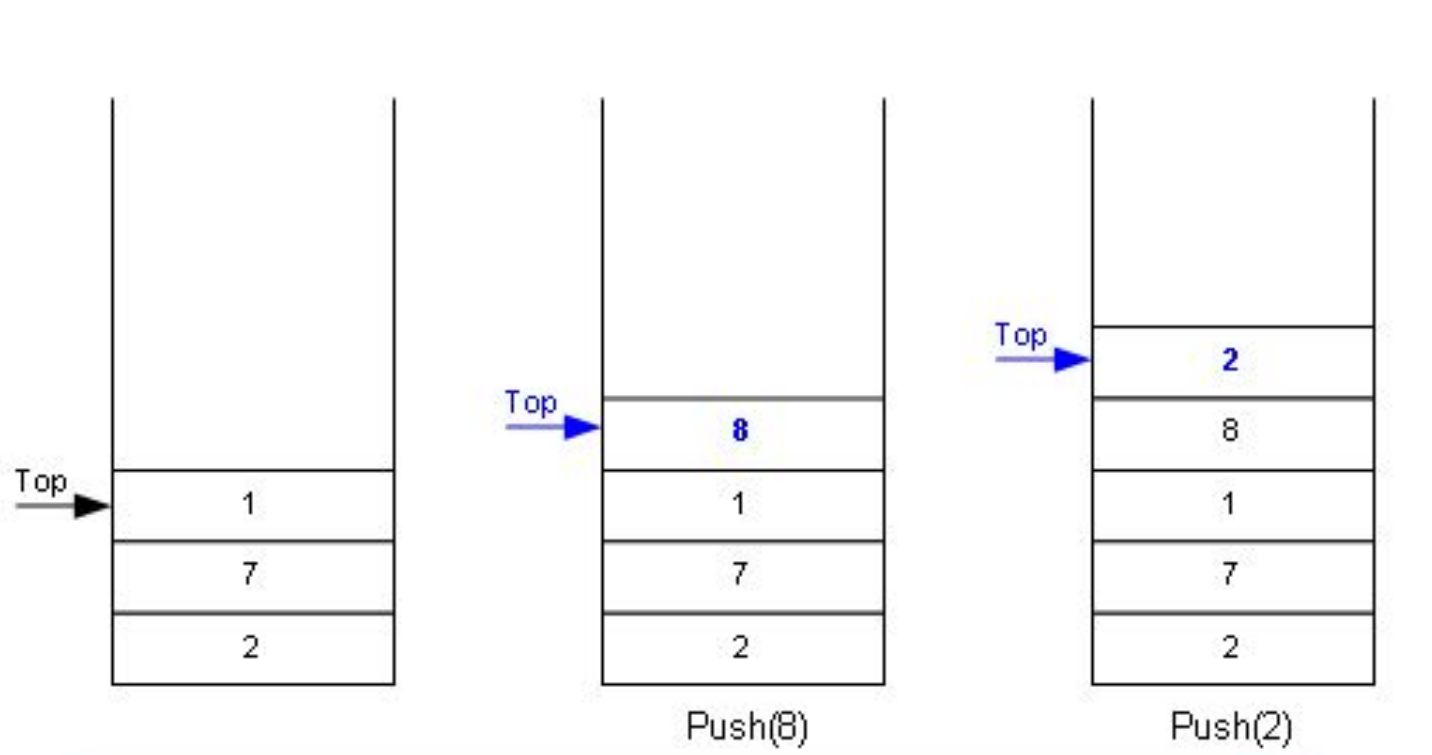

  • 出栈
    出栈就是在栈顶删除元素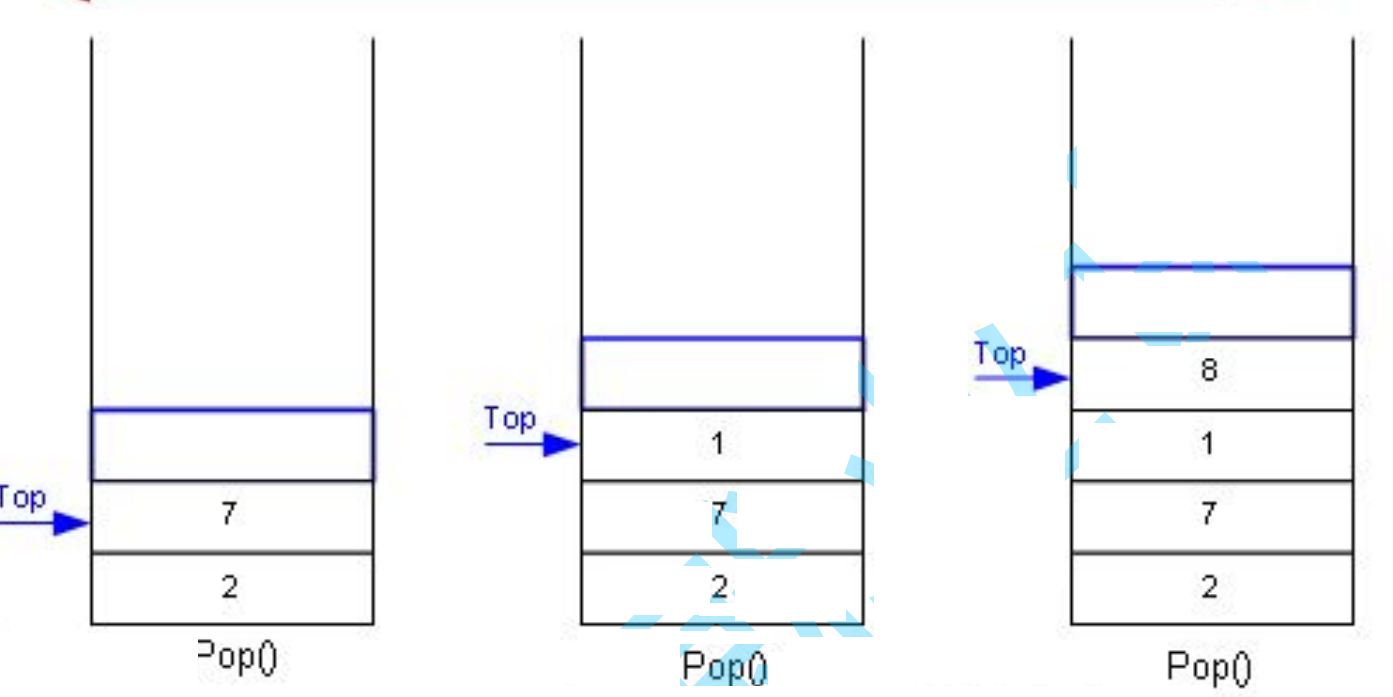

1.2栈的结构选择

  • 数组

我们可以用数组实现栈用下标控制栈顶元素的入栈和出栈

  • 单链表
    单链表其实不好实现栈，因为出栈时会修改上一个节点的指针。但单链表无法找到上一个节点。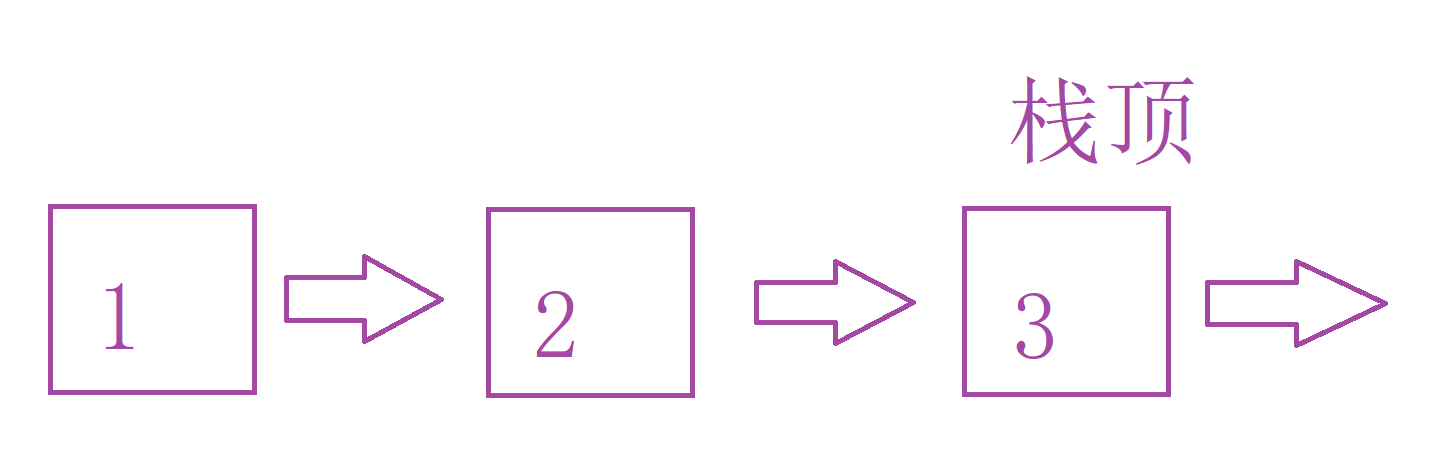

    所以我们把栈顶放在左边，栈顶是头节点，这样入栈出栈都可以。不需要修改上一个节点。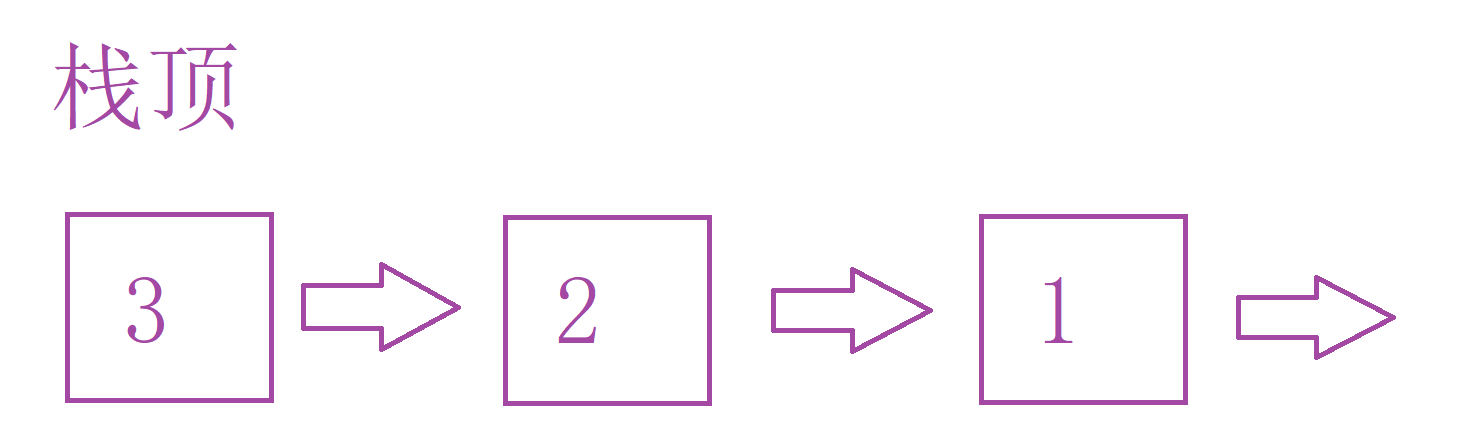
  • 双向链表
    为了解决单链表找上一个节点的问题，我们可以用双向链表来解决。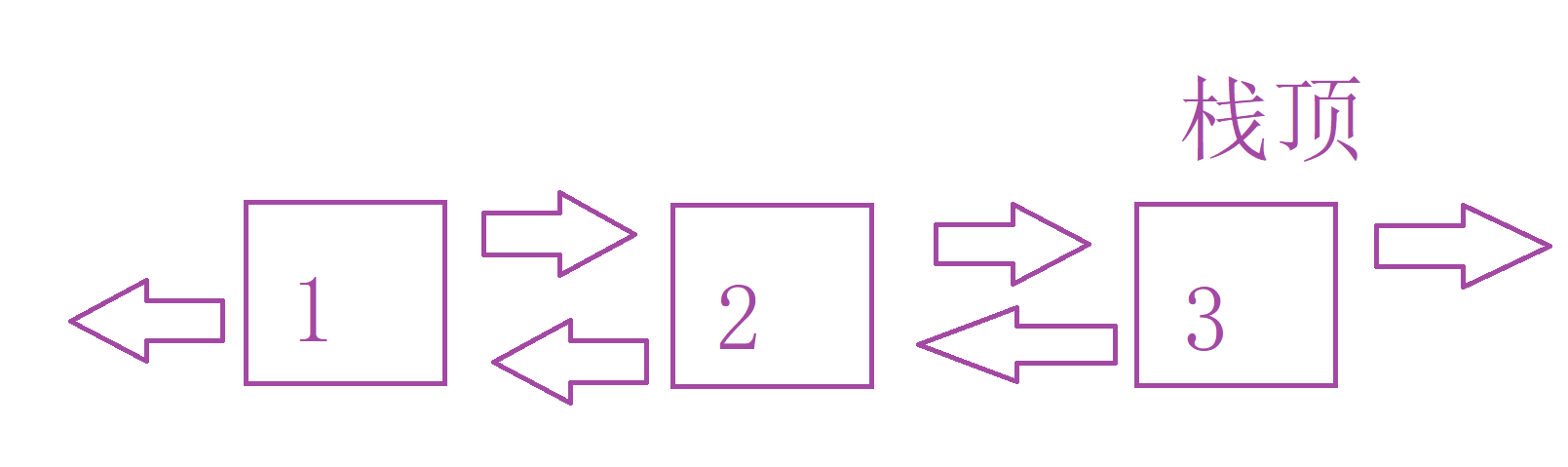

那这三个我们改选择那里一个呢？
首先我们可以先排除双向链表，因为它单链表还多了一个指针，多浪费了空间而且还要多维护一个指针。那单链表和数组我们选哪一个呢？其实都差不多。顺序表有扩容的问题。但是顺序表的缓存利用率高（文章有解释）。所以我们就选择数组吧。

1.3栈的实现

  • 栈的定义
    我们先定义一个栈结构体，里面放有栈数组的指针。top是栈顶元素的下标。capacity则是栈数组现在的空间大小。
typedef int STDataType; typedef struct Stack { 	STDataType* a; 	int top; 	int capacity; }ST;
  • 栈的初始化
    我们先断言一下。然后把空间大小和top都初始化为0。
    top的初始化有两种方式
void STInit(ST* pst) { 	assert(pst); 	pst->a = NULL; 	pst->capacity = pst->top = 0;//指向栈顶元素的下一个 }

一种是初始化为-1，代表top指向栈顶元素。为什么要给-1呢？
因为如果给0的话，当栈为空时，0既能表示栈为空也能代表栈有一个元素，下标为0。所以初始化要给-1。
第二种就是初始化给0，代表top指向栈顶元素的下一个位置。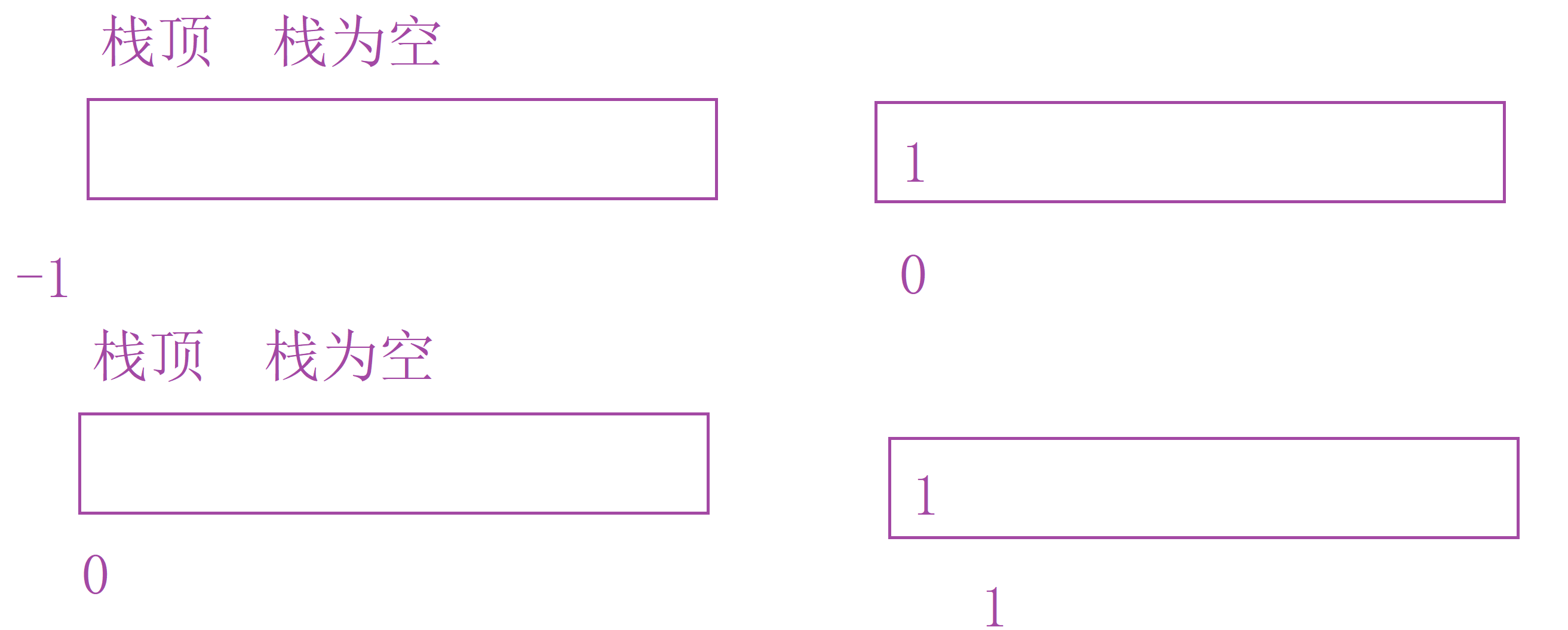

  • 栈的销毁

栈的销毁我们先free销毁数组，然后再给数组指针给空。
top和capacity都给0表示栈为空。

void STDestroy(ST* pst) { 	assert(pst); 	free(pst->a); 	pst->a = NULL; 	pst->capacity = pst->top = 0; }
  • 入栈
    入栈我们需要先对栈判满，如果满了我们就扩容到原来的2倍。
    如果没开空间就先开4个空间。当我们没开空间时,a是空指针，此时realloc相当与malloc。然后再更新a和capacity。赋值x，top++。
void STPush(ST* pst, STDataType x) { 	assert(pst); 	if (pst->capacity == pst->top)//栈满了 	{ 		int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;//未开空间就给4个空间，否则就在原来的空间扩容两倍 		STDataType* tmp = (STDataType*)realloc(pst->a,sizeof(STDataType)*newcapacity); 		if (tmp == NULL) 		{ 			perror("realloc fail~"); 			return; 		} 		pst->a = tmp; 		pst->capacity = newcapacity; 	} 	pst->a[pst->top++] = x;//赋值 top++ }
  • 出栈

出栈我们只需要控制top，让top–即可。

void STPop(ST* pst) { 	assert(pst); 	assert(pst->top > 0); 	pst->top--; }
  • 获取栈顶元素

因为我们top是指向栈顶元素的下一个，所以我们返回下标为top-1的元素

STDataType STTop(ST* pst) { 	assert(pst); 	assert(pst->top > 0); 	return pst->a[pst->top-1]; }
  • 判空

top等于0时就是空。

bool STEmpty(ST* pst) { 	assert(pst); 	return 0 == pst->top; }
  • 栈的元素个数
    因为我们的top指向栈顶元素的下一个，就相当于栈的元素个数size。
    我们直接返回top即可。
int STSize(ST* pst) { 	assert(pst); 	return pst->top; }
  • 栈的遍历
    栈在遍历的时候先获取栈顶元素，然后在出栈。直到栈为空。
int main() { 	ST s; 	STInit(&s); 	STPush(&s, 1); 	STPush(&s, 2); 	STPush(&s, 3); 	STPush(&s, 4); 	while (!STEmpty(&s)) 	{ 		printf("%d ", STTop(&s)); 		STPop(&s); 	} 	STDestroy(&s); 	return 0; }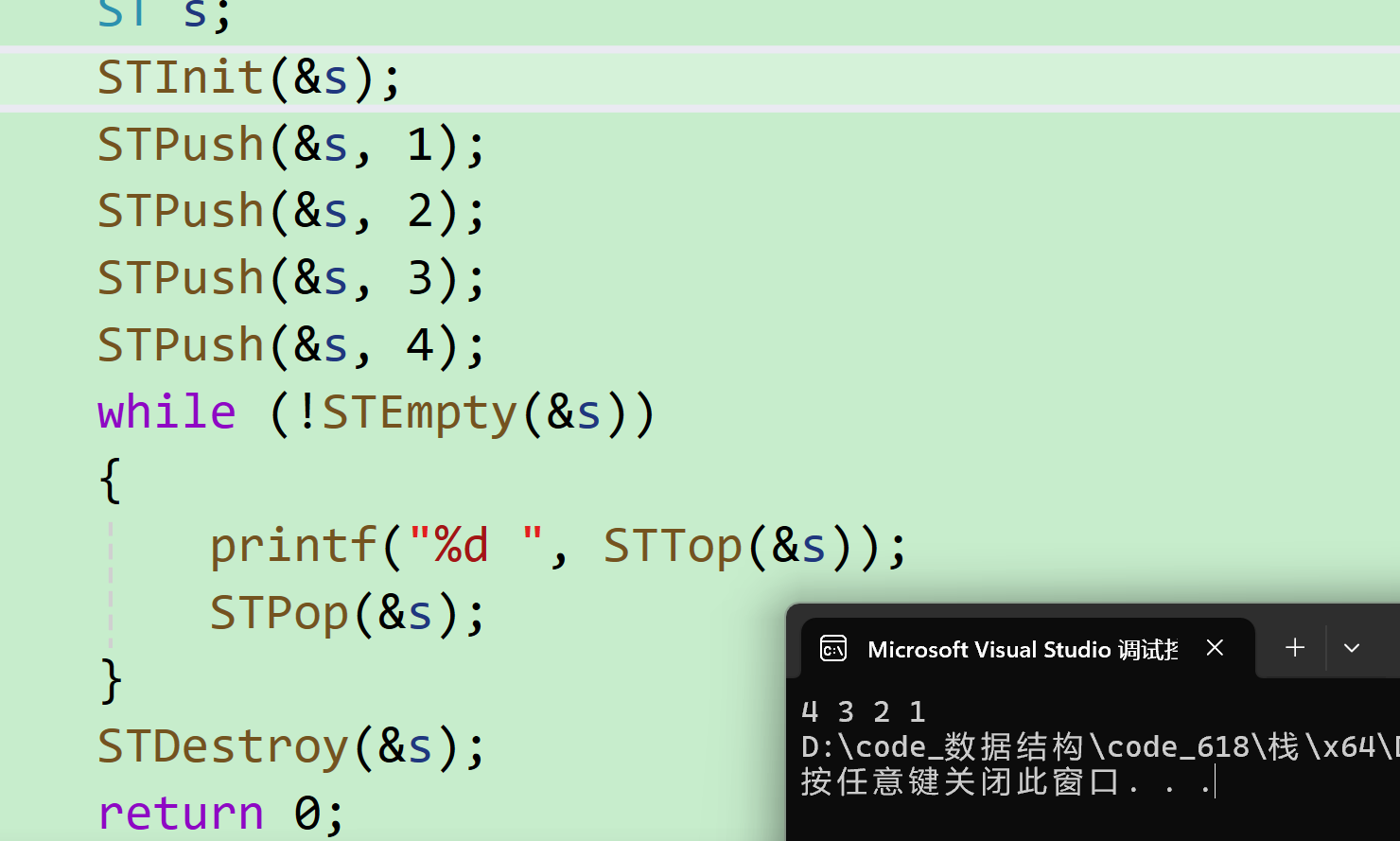


注意栈有可能边入边出，这时的输出结果顺序就不是与与输入顺序相反了

int main() { 	ST s; 	STInit(&s); 	STPush(&s, 1); 	STPush(&s, 2); 	printf("%d ", STTop(&s)); 	STPop(&s); 	STPush(&s, 3); 	STPush(&s, 4); 	while (!STEmpty(&s)) 	{ 		printf("%d ", STTop(&s)); 		STPop(&s); 	} 	STDestroy(&s); 	return 0; }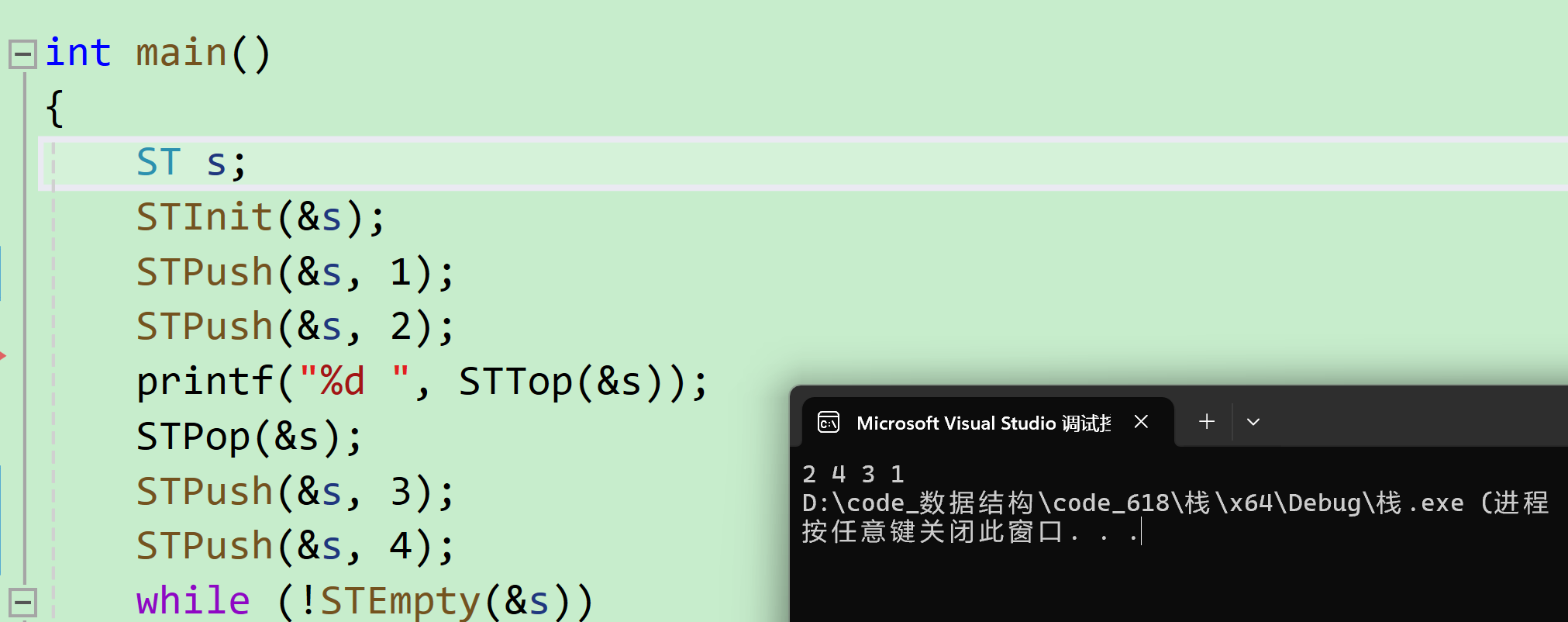

1.4栈OJ

-题目
有效的括号

  • 思路分析
    让左括号入栈，右括号与左括号匹配。

  • 代码实现

typedef char STDataType; typedef struct Stack { 	STDataType* a; 	int top; 	int capacity; }ST; void STInit(ST* pst) { 	assert(pst); 	pst->a = NULL; 	pst->capacity = pst->top = 0; } void STDestroy(ST* pst) { 	assert(pst); 	free(pst->a); 	pst->a = NULL; 	pst->capacity = pst->top = 0; } void STPush(ST* pst, STDataType x) { 	assert(pst); 	if (pst->capacity == pst->top) 	{         int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity; 		STDataType* tmp = (STDataType*)realloc(pst->a,sizeof(STDataType)*newcapacity); 		if (tmp == NULL) 		{ 			perror("realloc fail~"); 			return; 		} 		pst->a = tmp; 		pst->capacity = newcapacity; 	} 	pst->a[pst->top++] = x; } void STPop(ST* pst) { 	assert(pst); 	assert(pst->top > 0); 	pst->top--; } STDataType STTop(ST* pst) { 	assert(pst); 	assert(pst->top > 0); 	return pst->a[pst->top-1]; } bool STEmpty(ST* pst) { 	assert(pst); 	return 0 == pst->top; } int STSize(ST* pst) { 	assert(pst); 	return pst->top; } bool isValid(char* s)  {     ST t;     STInit(&t);     while(*s)     {         if(*s=='('||*s=='['||*s=='{')         {             STPush(&t,*s);//左括号入栈         }         else         {             if(STEmpty(&t))//没有左括号匹配             {                 return false;             }            char tmp=STTop(&t);//获取栈顶元素匹配            STPop(&t);            if(*s==')'&&tmp!='('            ||*s=='}'&&tmp!='{'            ||*s==']'&&tmp!='[')//匹配            {              return false;            }         }         s++;     }     bool ret=STEmpty(&t);//判空     STDestroy(&t);     return ret;  }
  • 题目
    用栈实现队列
  • 思路分析

    因为栈导数据到另一个栈后，数据相反。由后进先出边先进先出。所以我们固定一个栈入数据，一个栈出数据即可。
  • 代码实现
typedef int STDataType; typedef struct Stack { 	STDataType* a; 	int top; 	int capacity; }ST; void STInit(ST* pst) { 	assert(pst); 	pst->a = NULL; 	pst->capacity = pst->top = 0; } void STDestroy(ST* pst) { 	assert(pst); 	free(pst->a); 	pst->a = NULL; 	pst->capacity = pst->top = 0; } void STPush(ST* pst, STDataType x) { 	assert(pst); 	if (pst->capacity == pst->top) 	{ 		int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity; 		STDataType* tmp = (STDataType*)realloc(pst->a,sizeof(STDataType)*newcapacity); 		if (tmp == NULL) 		{ 			perror("realloc fail~"); 			return; 		} 		pst->a = tmp; 		pst->capacity = newcapacity; 	} 	pst->a[pst->top++] = x; } void STPop(ST* pst) { 	assert(pst); 	assert(pst->top > 0); 	pst->top--; } STDataType STTop(ST* pst) { 	assert(pst); 	assert(pst->top > 0); 	return pst->a[pst->top-1]; } bool STEmpty(ST* pst) { 	assert(pst); 	return 0 == pst->top; } int STSize(ST* pst) { 	assert(pst); 	return pst->top; } typedef struct {     ST pushst;     ST popst; } MyQueue; MyQueue* myQueueCreate() {     MyQueue* pq=malloc(sizeof(MyQueue));     STInit(&pq->pushst);     STInit(&pq->popst);     return pq; } void myQueuePush(MyQueue* obj, int x) {     STPush(&obj->pushst,x); } int myQueuePeek(MyQueue* obj) {     if(STEmpty(&obj->popst))     {         while(!STEmpty(&obj->pushst))         {             int top=STTop(&obj->pushst);             STPush(&obj->popst,top);             STPop(&obj->pushst);         }     }     int top=STTop(&obj->popst);     return top; } int myQueuePop(MyQueue* obj) {    int ret=myQueuePeek(obj);    STPop(&obj->popst);    return ret; } bool myQueueEmpty(MyQueue* obj) {     return STEmpty(&obj->pushst)&&STEmpty(&obj->popst); } void myQueueFree(MyQueue* obj) {     STDestroy(&obj->pushst);     STDestroy(&obj->popst);     free(obj);     obj=NULL; }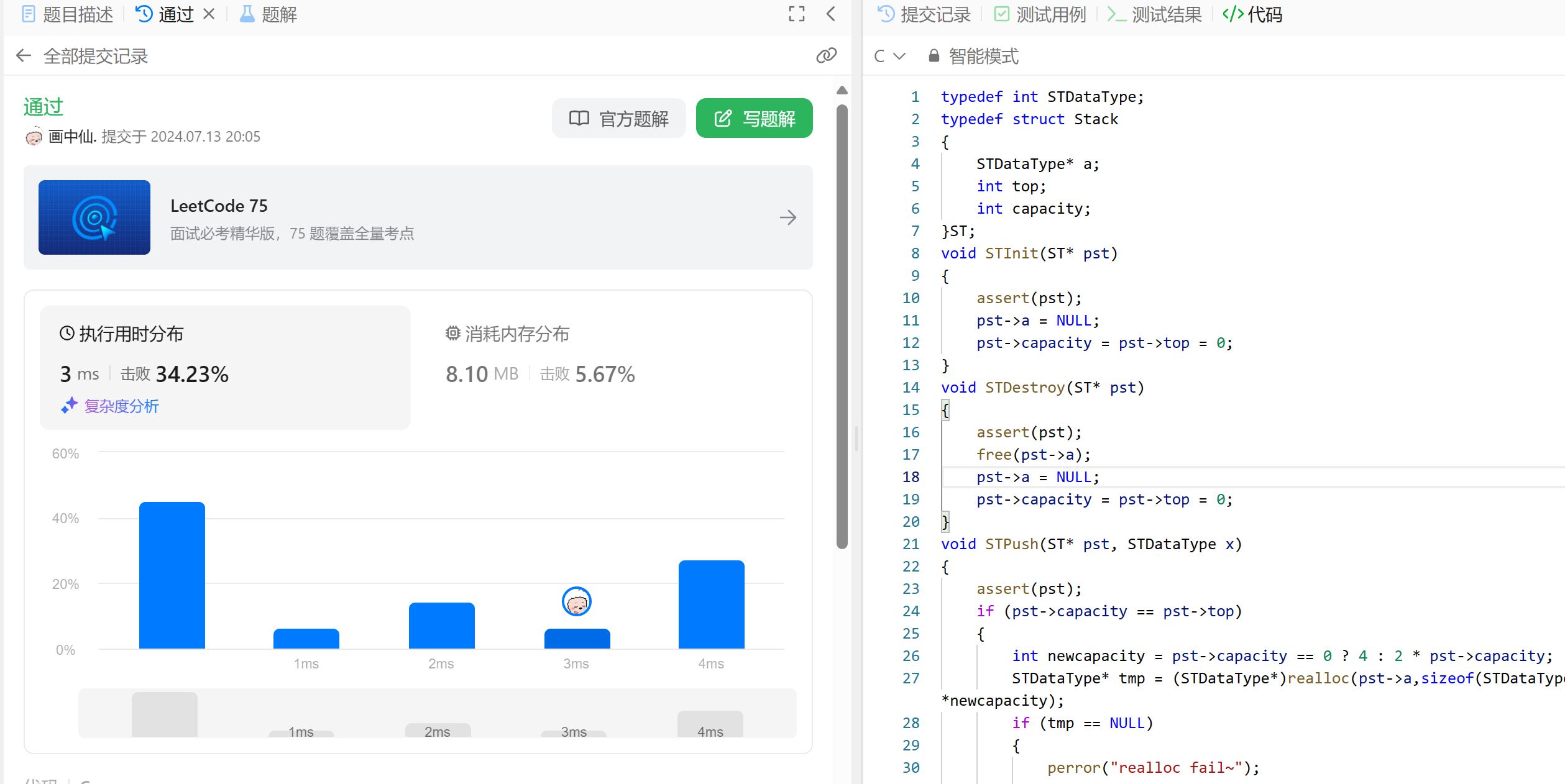

二. 队列

2.1队列的概念及结构

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out)
入队列：进行插入操作的一端称为队尾
出队列：进行删除操作的一端称为队头


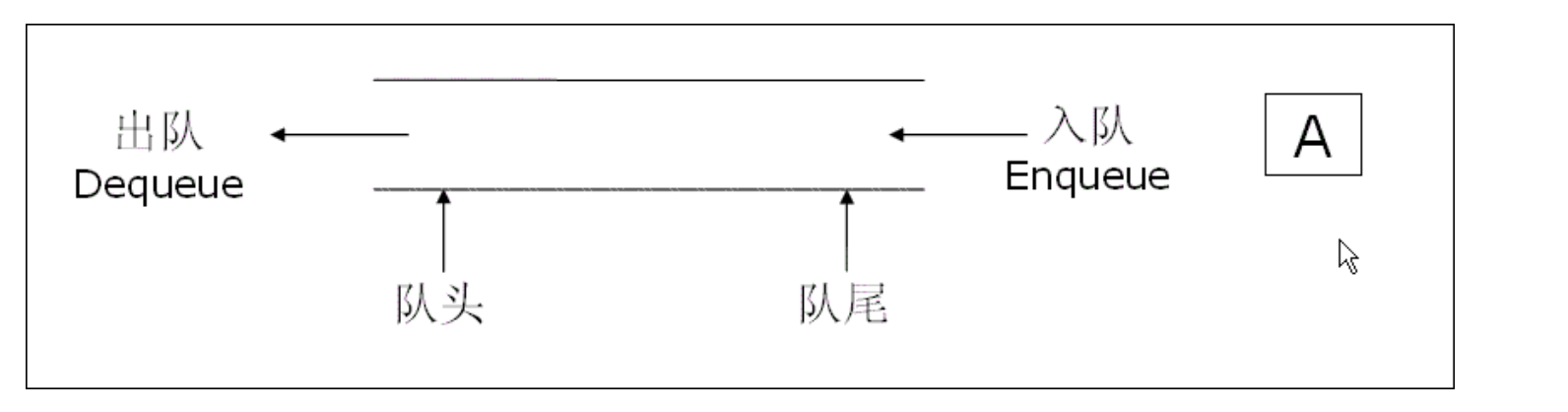
与栈相反，队列遵循先进先出的原则。只能在队尾入数据，队头出数据。

2.2队列的应用

  • 抽号机
    我们平时在日常生活中都会遇到取票排队。取票后我们就把票数尾插到抽号机里，要取票时我们就在队头出数据。这样就能保证先取票的先出号。
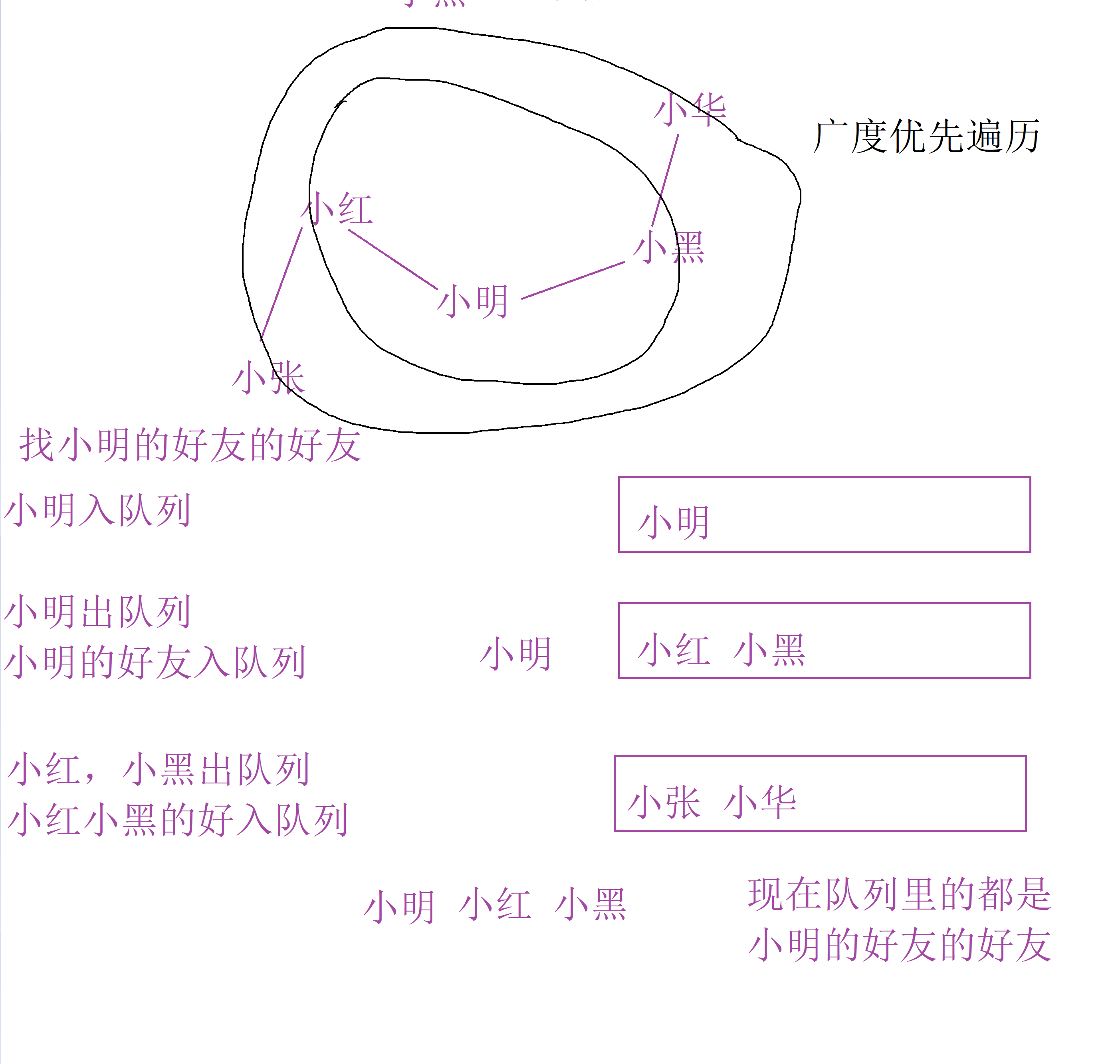
  • 好友推荐
    队列还可以做好友推荐。也就是广度优先遍历（DFS）。

2.3队列的选择

  • 顺序表
    顺序表不好实现队列。因为队列是队头出数据，顺序表头删需要挪动数据。

  • 双向链表
    双向链表其实实现啥都好。但是双向链表多开一个指针，浪费内存。还要多维护一个指针。

  • 单链表
    单链表实现队列非常合适。因为队列在队尾入数据，队头出数据。单链表头删和尾删都不需要上一个节点。

所以我们用单链表实现。

2.4队列的实现

  • 队列结构体
    我们先定义一个队列节点的结构体，然后在用一个头指针，一个尾指针，和一个size维护整个队列。
typedef struct QueueNode { 	struct QueueNode* next; 	QDataType val; }QNode; typedef struct Queue { 	QNode* phead; 	QNode* ptail; 	int size; }Queue;
  • 队列的初始化
    我们把头指针和尾指针都初始化为空，size初始化为0.
void QueueInit(Queue* pq) { 	assert(pq); 	pq->phead = pq->ptail = NULL; 	pq->size = 0; }
  • 队列的销毁

我们创建一个cur指针指向头节点，然后遍历销毁即可。注意要先保存下一个节点在销毁当前节点，然后移动cur即可。最后让头指针尾指针指向空。size为0即可。

void QueueDestroy(Queue* pq) { 	assert(pq); 	QNode* cur = pq->phead; 	while (cur) 	{ 		QNode* next = cur->next; 		free(cur); 		cur = next; 	}; 	pq->phead = pq->ptail = NULL; 	pq->size = 0; }
  • 队列的插入
    我们malloc一个节点。因为是尾插，所以让节点指向空。赋值为x。如果没有节点，那头节点和尾节点都是指向新节点。否则尾插在尾节点后。新节点成为新的尾节点。最后size++。
void QueuePush(Queue* pq, QDataType x) { 	assert(pq); 	QNode* node = (QNode*)malloc(sizeof(QNode)); 	if (node == NULL) 	{ 		perror("malloc fail"); 		return; 	} 	node->next = NULL; 	node->val = x; 	if (pq->phead == NULL)//没有节点 	{ 		pq->phead = pq->ptail = node; 	} 	else//至少有一个节点 	{ 		pq->ptail->next = node; 		pq->ptail = node; 	} 	pq->size++; }

-获取队头元素

我们先断言一下判断队列是否为空，然后返回队头节点元素的值。

QDataType QueueFron(Queue* pq) { 	assert(pq); 	assert(pq->size != 0); 	return pq->phead->val; }
  • 获取队尾元素
    我们先断言一下判断队列是否为空，然后返回队尾节点元素的值。
QDataType QueueBack(Queue* pq) { 	assert(pq); 	assert(pq->size != 0); 	return pq->ptail->val; }
  • 队头的删除
    我们先断言一下判断队列是否为空，然后分两种情况
    第一种情况，当队列只有一个节点时。
    队头指针和队尾指针都指向空，size–。
    第二种情况，当队列不是一个节点时。
    保存队头节点的下一个节点，释放头节点，保存的节点成为新的头节点。size–。
void QueuePop(Queue* pq) { 	assert(pq); 	assert(pq->size != 0); 	if (pq->phead == pq->ptail)//只有一个节点 	{ 		free(pq->phead); 		pq->phead = pq->ptail = NULL; 		pq->size--; 	} 	else 	{ 		QNode* next = pq->phead->next; 		free(pq->phead); 		pq->phead = next; 		pq->size--; 	} }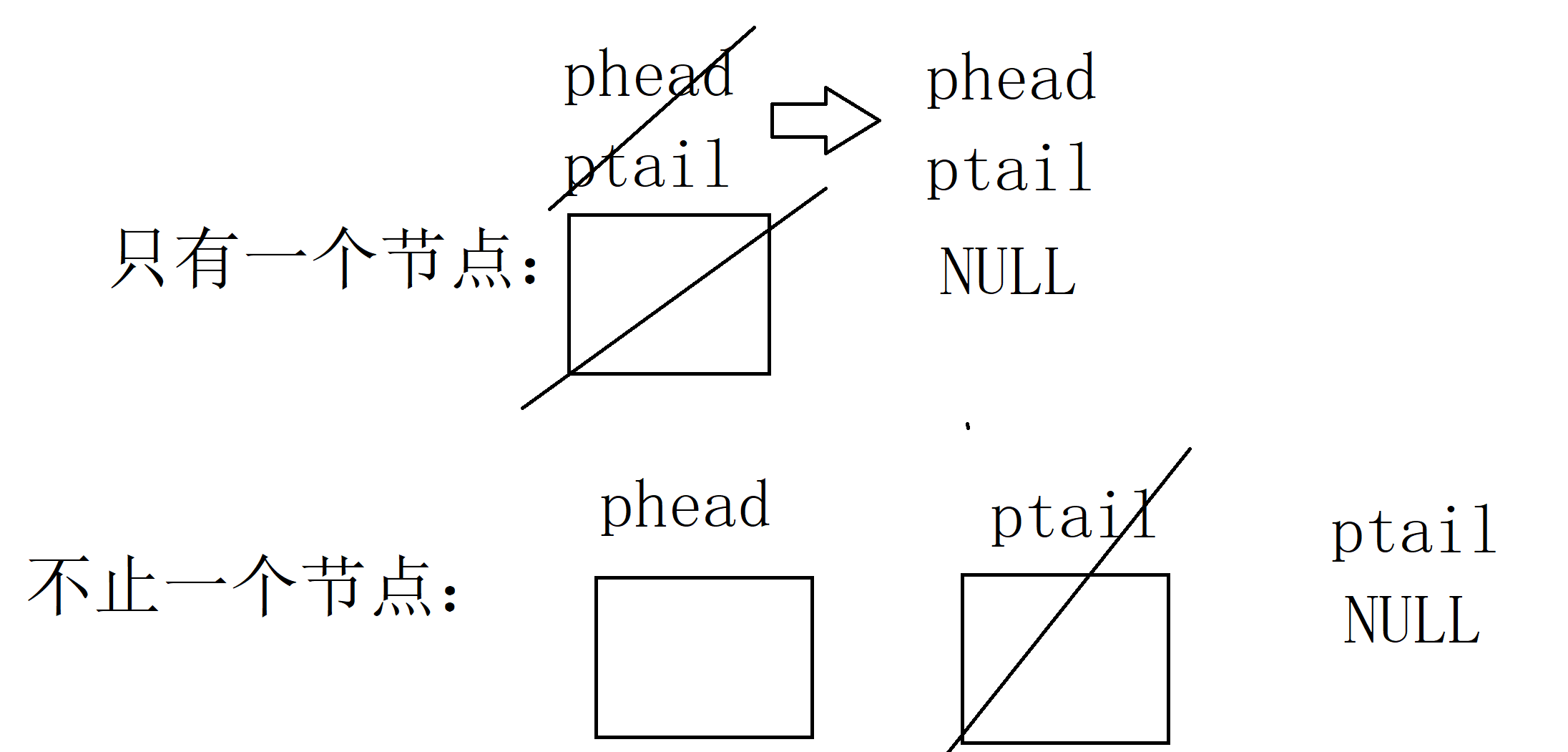

  • 队列的判空

判断size是否为0即可

bool QueueEmpty(Queue* pq) { 	assert(pq); 	return pq->size == 0; }
  • 队列的元素个数

因为我们前面用size记录了个数，直接返回size即可。
防止遍历找.实现O(1).

int QueueSize(Queue* pq) { 	assert(pq); 	return pq->size; }
  • 队列的遍历

队列的遍历就是获取队头元素，然后删除队头元素直到队列为空。

int main() { 	Queue q; 	QueueInit(&q); 	QueuePush(&q, 1); 	QueuePush(&q, 2); 	QueuePush(&q, 3); 	QueuePush(&q, 4); 	while (q.size) 	{ 		printf("%d ", QueueFron(&q)); 		QueuePop(&q); 	} 	QueueDestroy(&q); 	return 0; }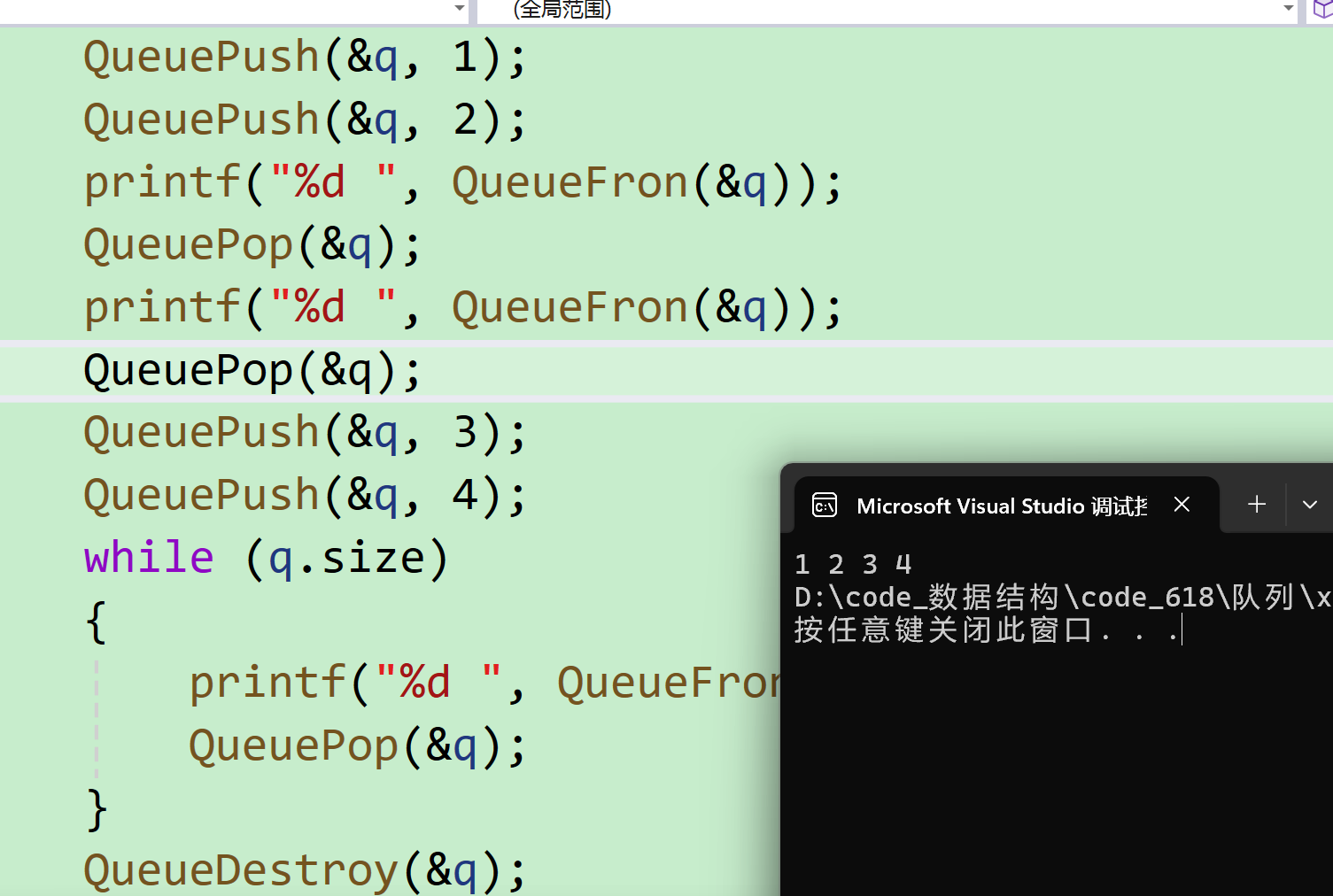

注意不论是否边入边出。队列输出的顺序都与入队列顺序一致。

int main() { 	Queue q; 	QueueInit(&q); 	QueuePush(&q, 1); 	QueuePush(&q, 2); 	printf("%d ", QueueFron(&q)); 	QueuePop(&q); 	printf("%d ", QueueFron(&q)); 	QueuePop(&q); 	QueuePush(&q, 3); 	QueuePush(&q, 4); 	while (q.size) 	{ 		printf("%d ", QueueFron(&q)); 		QueuePop(&q); 	} 	QueueDestroy(&q); 	return 0; }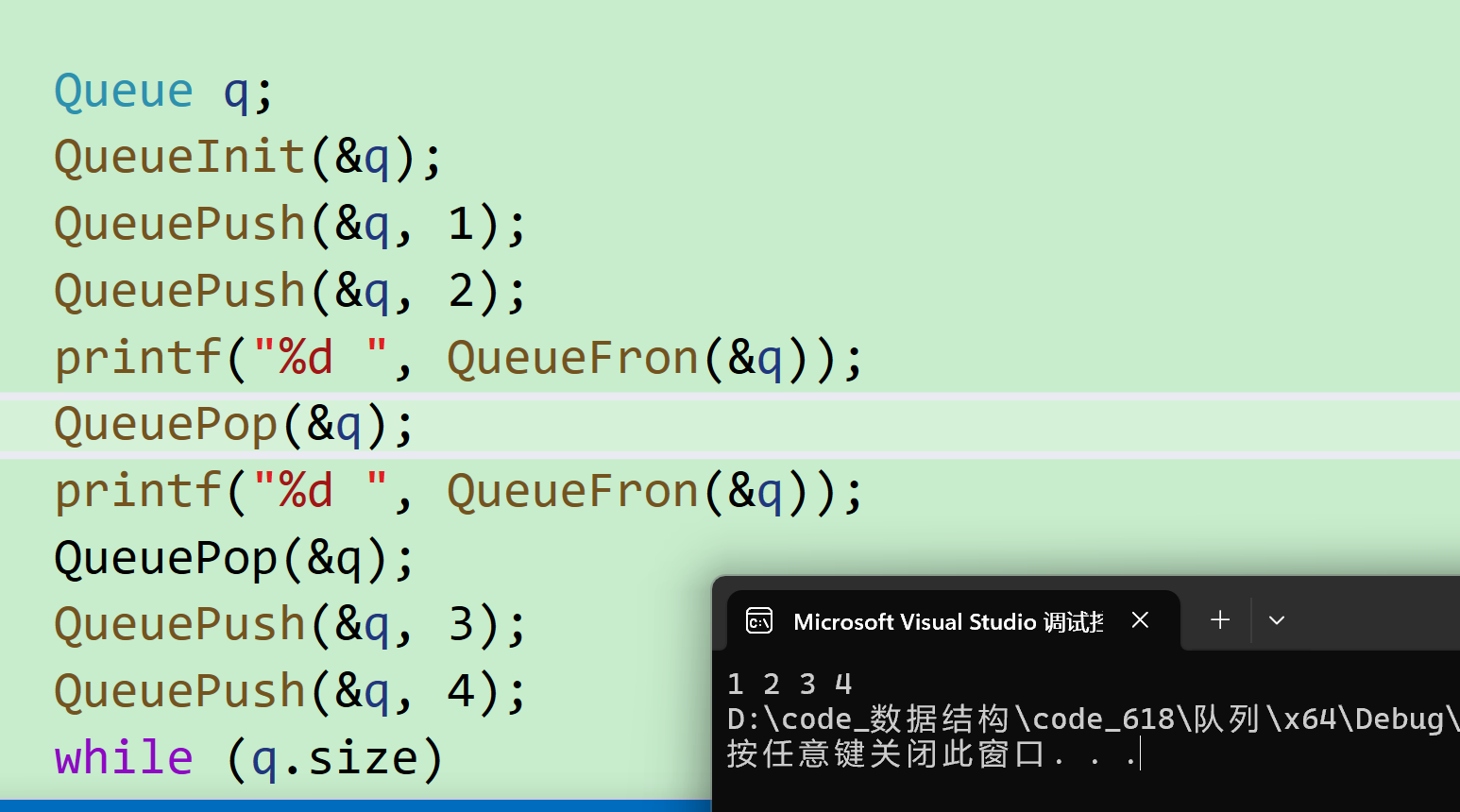

2.5队列OJ

  • 题目
    用队列实现栈

  • 思路分析
    我们保持一个队列有数据，一个队列没数据。
    出栈时，往空队列导入数据即可拿到栈顶元素。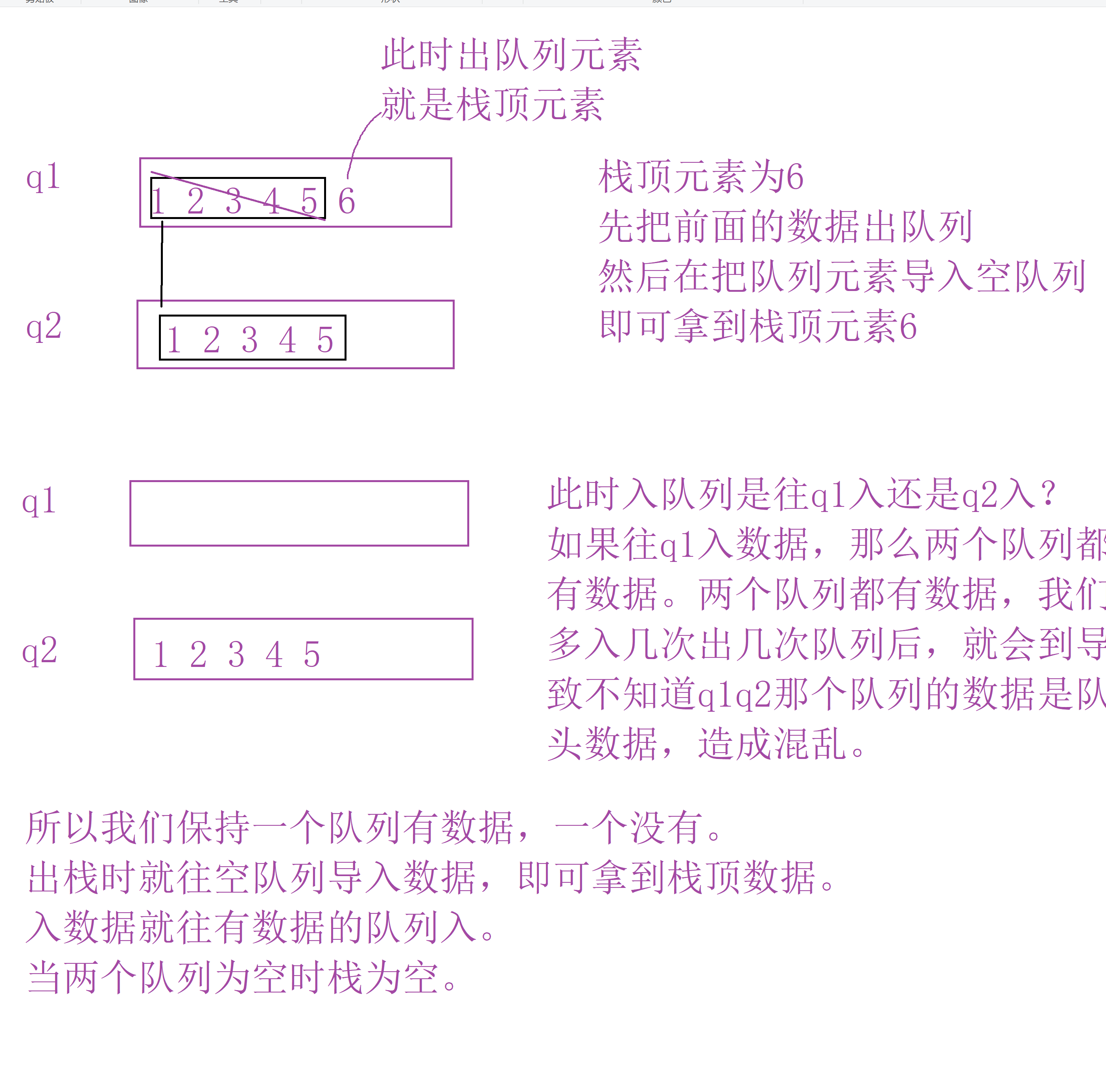

  • 代码实现

typedef int QDataType; typedef struct QueueNode { 	struct QueueNode* next; 	QDataType val; }QNode; typedef struct Queue { 	QNode* phead; 	QNode* ptail; 	int size; }Queue; void QueueInit(Queue* pq) { 	assert(pq); 	pq->phead = pq->ptail = NULL; 	pq->size = 0; } void QueueDestroy(Queue* pq) { 	assert(pq); 	QNode* cur = pq->phead; 	while (cur) 	{ 		QNode* next = cur->next; 		free(cur); 		cur = next; 	}; 	pq->phead = pq->ptail = NULL; 	pq->size = 0; } void QueuePush(Queue* pq, QDataType x) { 	assert(pq); 	QNode* node = (QNode*)malloc(sizeof(QNode)); 	if (node == NULL) 	{ 		perror("malloc fail"); 		return; 	} 	node->next = NULL; 	node->val = x; 	if (pq->phead == NULL) 	{ 		pq->phead = pq->ptail = node; 	} 	else 	{ 		pq->ptail->next = node; 		pq->ptail = node; 	} 	pq->size++; } QDataType QueueFron(Queue* pq) { 	assert(pq); 	assert(pq->size != 0); 	return pq->phead->val; } QDataType QueueBack(Queue* pq) { 	assert(pq); 	assert(pq->size != 0); 	return pq->ptail->val; } bool QueueEmpty(Queue* pq) { 	assert(pq); 	return pq->size == 0; } void QueuePop(Queue* pq) { 	assert(pq); 	assert(pq->size != 0); 	if (pq->phead == pq->ptail) 	{ 		free(pq->phead); 		pq->phead = pq->ptail = NULL; 		pq->size--; 	} 	else 	{ 		QNode* next = pq->phead->next; 		free(pq->phead); 		pq->phead = next; 		pq->size--; 	} } //统计个数 int QueueSize(Queue* pq) { 	assert(pq); 	return pq->size; } typedef struct {     Queue q1;     Queue q2; } MyStack; MyStack* myStackCreate() {     MyStack* q=(MyStack*)malloc(sizeof(MyStack));     QueueInit(&(q ->q1));     QueueInit(&(q->q2));     return q; } void myStackPush(MyStack* obj, int x) {     if(!QueueEmpty(&obj->q1))//往不为空的队列入数据     {         QueuePush(&obj->q1,x);     }     else     {         QueuePush(&obj->q2,x);     } } int myStackPop(MyStack* obj) {     Queue* empty=&obj->q1;     Queue* noempty=&obj->q2;     if(!QueueEmpty(&obj->q1))     {         noempty=&obj->q1;         empty=&obj->q2;     }//假设法     while(QueueSize(noempty)>1)//数据入队列直到剩下一个数据     {         QueuePush(empty,QueueFron(noempty));         QueuePop(noempty);     }     int top=QueueFron(noempty);     QueuePop(noempty);     return top; } int myStackTop(MyStack* obj) {     if(!QueueEmpty(&obj->q1))//返回不为空的队尾元素     {         return QueueBack(&obj->q1);     }     else     {         return QueueBack(&obj->q2);     } } bool myStackEmpty(MyStack* obj) {     return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);//判断两个队列是否为空 } void myStackFree(MyStack* obj) {     QueueDestroy(&obj->q1);//销毁队列1     QueueDestroy(&obj->q2);//销毁队列2     free(obj);//销毁结构体     obj=NULL; }
  • 题目

设计循环队列

  • 思路分析


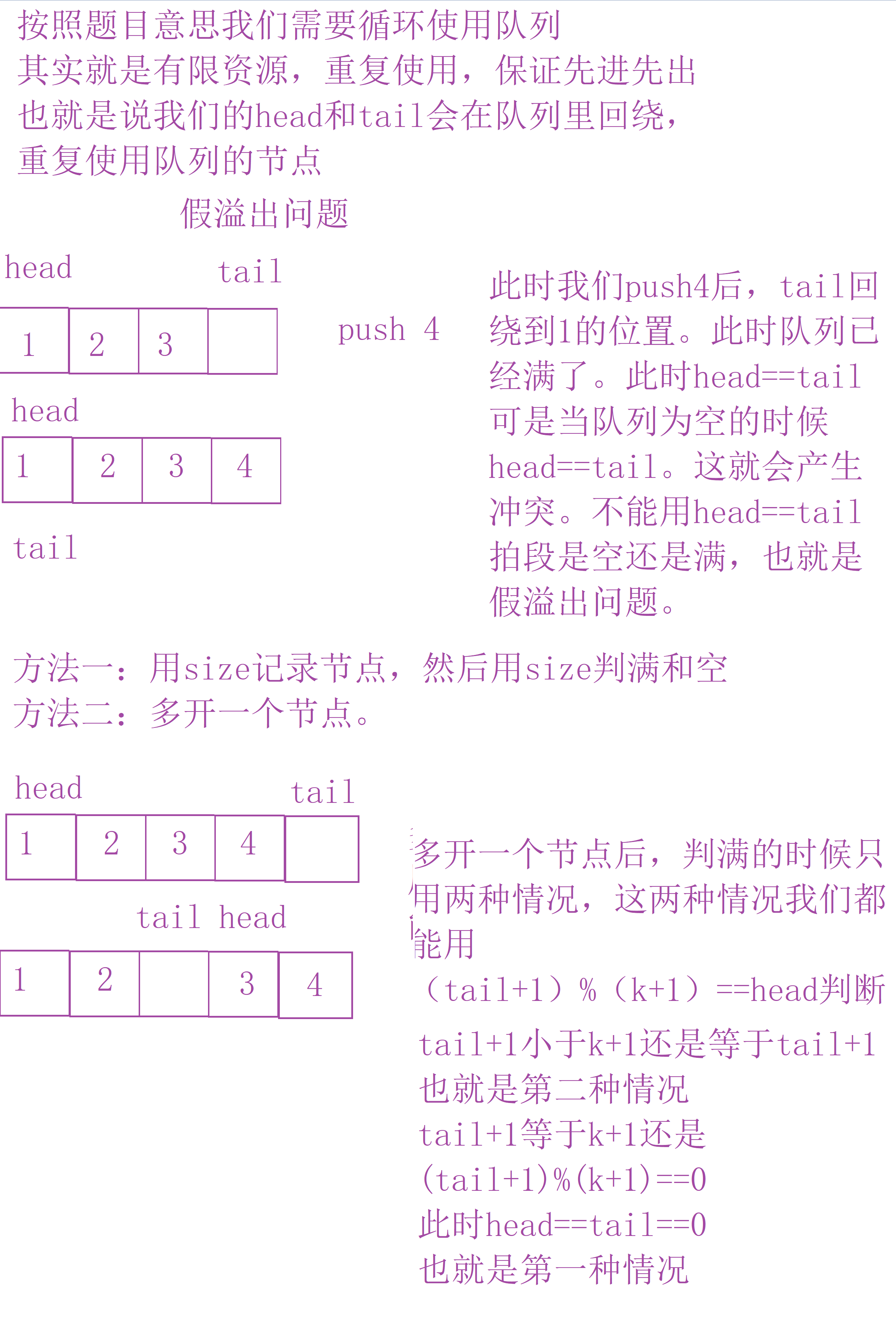
主要就是回绕的问题和假溢出的问题

  • 队列结构体
    这里我们用一个数组指针指向队列，一个head和tail控制队列的头和尾。在记录一个k表示循环队列长度。
typedef struct {     int* a;     int head;     int tail;     int k; } MyCircularQueue;
  • 队列初始化
    malloc一个队列结构体，在malloc一个队列。k+1多开一个空间解决假溢出问题。然后初始化head和tail为0。赋值k。
MyCircularQueue* myCircularQueueCreate(int k) {     MyCircularQueue* pq=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));     pq->a=(int*)malloc(sizeof(int)*(k+1));     pq->head=0;     pq->tail=0;     pq->k=k;     return pq; }
  • 队列判空
    当head==tail时队列为空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {     return obj->head==obj->tail; }
  • 队列判满

当(tail+1)%(k+1)==head时为满。
%(k+1)是为了解决回绕的问题。

bool myCircularQueueIsFull(MyCircularQueue* obj) {     return (obj->tail+1)%(obj->k+1)==obj->head; }
  • 队列的插入

先判断队列是否为满。如果不满就直接在tail的位置插入，然后tail+1继续%k+1解决回绕。

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {      if (!myCircularQueueIsFull(obj))      {         obj->a[obj->tail] = value;         obj->tail = (obj->tail + 1) % (obj->k + 1);         return true;      }      return false; }
  • 队列的删除

先判空。队列的删除直接让head+1%k+1解决回绕即可。

bool myCircularQueueDeQueue(MyCircularQueue* obj) {     if (!myCircularQueueIsEmpty(obj))     {        obj->head  = (obj->head + 1) % (obj->k + 1);        return true;     }       return false; }
  • 队列的队头元素

先判空。不为空直接返回下标为head的值

int myCircularQueueFront(MyCircularQueue* obj) {     if(myCircularQueueIsEmpty(obj))     {         return -1;     }     return obj->a[obj->head]; }
  • 队列的队尾元素
int myCircularQueueRear(MyCircularQueue* obj) {     if(myCircularQueueIsEmpty(obj))     {         return -1;     }     return obj->a[(obj->tail-1+obj->k+1)%(obj->k+1)]; }

正常情况我们可以直接返回下标为tail-1的值。可是会有越界的情况

  • 队列的销毁

先把队列数组销毁，然后销毁队列结构体即可。

void myCircularQueueFree(MyCircularQueue* obj) {     free(obj->a);     obj->a=NULL;     free(obj);     obj=NULL; }

后言

这就是栈和队列的内容。栈和队列都是很重要的数据结构。大家一定要多加掌握和熟练。今天就分享到这里。感谢大家的耐心垂阅，咱们下期见！拜拜~
在这里插入图片描述

相关阅读
  1. 如何查看和设置我的Android N设备的权限？
  2. 如何在安卓手机上自定义应用图标？
  3. 如何在安卓微信中同时听语音和查看图片？
  4. 华为哪些设备将支持升级至安卓7.0？
  5. 微信安卓软件中Q10功能有哪些独特之处？
  6. 安卓用户如何挑选最佳视频播放器应用？
  7. 安卓系统中用户文件目录的确切位置是什么？
  8. 小米4用户如何安全升级到安卓8.0系统？
  9. 如何成功将魅蓝5升级至安卓原生7.0版本？
  10. 16GB存储的安卓手机是否能满足日常需求？

广告一刻

为您即时展示最新活动产品广告消息，让您随时掌握产品活动新动态！