找往期文章包括但不限于本期文章中不懂的知识点:
个人主页:我要学编程(ಥ_ಥ)-CSDN博客
所属专栏:数据结构(Java版)
目录
队列有关概念
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 的特点。
入队列:进行插入操作的一端称为队尾(Tail/Rear) ;
出队列:进行删除操作的一端称为队头 (Head/Front)。
队列和我们在日常生活中买东西排队或者在食堂打饭的场景是一样的。如下图:
队列的使用
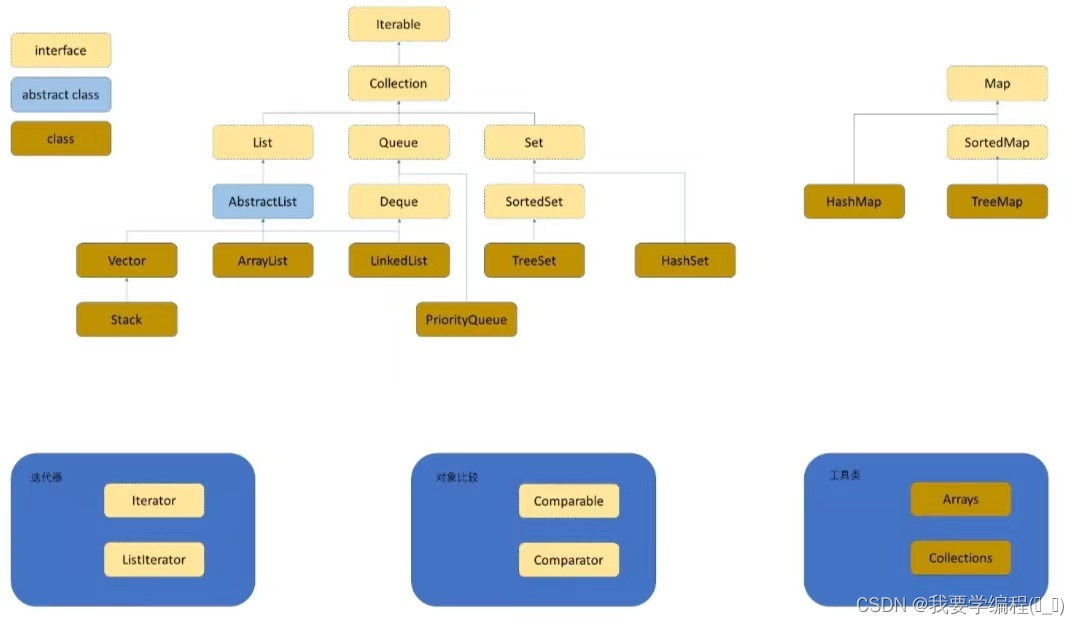
上面这张图中,Queue 便是队列,可以看到其底层是 LinkedList ,也就是双向链表实现的。
| 方法 | 功能 |
| boolean offer(E e) | 往队尾添加元素 |
| E poll() | 获取并删除队头元素 |
| peek() | 获取队头元素 |
| int size() | 获取队列中有效元素个数 |
| boolean isEmpty() | 检测队列是否为空 |
public class Test { public static void main(String[] args) { Queue<Integer> queue = new LinkedList<>(); // 判断队列是否为空 System.out.println(queue.isEmpty()); // 往队尾插入元素 queue.offer(1); queue.offer(2); queue.offer(3); queue.offer(4); queue.offer(5); // 获得并删除对头元素 System.out.println(queue.poll()); // 获取对头元素 System.out.println(queue.peek()); // 判断队列是否为空 System.out.println(queue.isEmpty()); int x = queue.size(); System.out.println(x); // 循环遍历队列中的元素并删除 for (int i = 0; i < x; i++) { System.out.print(queue.poll()+" "); } System.out.println(); // 注意这个poll()方法并不会因为队列为空而抛出空指针异常 System.out.println(queue.poll()); } } 因为上面代码中队列是用 LinkedList 实现的,那么我们就应该去其源码下,查看 poll() 方法

队列模拟实现
// 用链表模拟实现队列 public class MyQueue { static class ListNode { int val; ListNode prev; ListNode next; public ListNode(int val) { this.val = val; } } public ListNode head; public ListNode last; public int size; // 减少时间复杂度去遍历链表 // 往队尾添加元素 public boolean offer(int val) { // 创建一个新的节点 ListNode newNode = new ListNode(val); // 队列为空 if (head == null) { head = newNode; last = newNode; } else { // 就是在链表中尾插元素 last.next = newNode; newNode.prev = last; last = last.next; } size++; return true; } // 删除并获取对头元素 public Integer poll() { // 链表为空就返回null if (head == null) { return null; } else { int x = head.val; size--; // 链表中只有一个元素就直接删除 if (head.next == null) { head = null; last = null; return x; } else { // 链表中有多个节点 head = head.next; return x; } } } // 获取对头元素 public Integer peek() { // 模范源码的写法 return head == null ? null : head.val; } // 获取节点个数 public int size() { return size; } // 检测链表是否为空 public boolean isEmpty() { return head == null; } } 上面是用链表模拟实现,队列用链表实现时,就可以把队列看成是一个链表,我们就可以用实现链表的方式来实现队列。又因为链表是用节点组成,因此,我们就要创建节点,来操作链表。
接下来,我们就可以尝试用数组来实现队列。
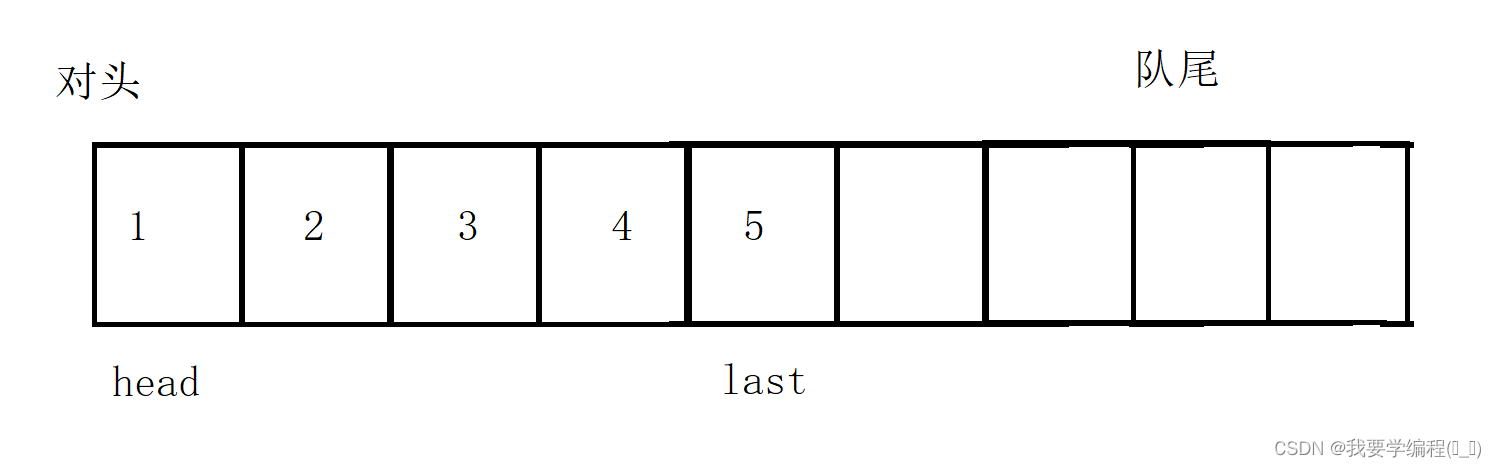
上面这个数组看起来虽然可以实现队列,但是我们如果去写队列的方法时,根本无法实现。因为删除对头元素时,last到底要不要 -1 呢?如果 -1,那么last 就会指向5位置的下标,不符合要求;如果不 -1,那么对头元素该怎么办呢?有小伙伴可能会说,直接把元素从后往前覆盖,然后再把 last -1,不就完事了吗? 但又有一个问题:移动数组元素所付出的时间是非常大的,因为队列中出队的元素永远是数组的首元素,在移动数组时,全部的元素都得移动,这就会浪费很多的时间。因此上面这种方法是不可行的,就得用一种全新的数组来解决:循环数组。用循环数组实现的队列也叫作循环队列。
循环队列的模拟实现
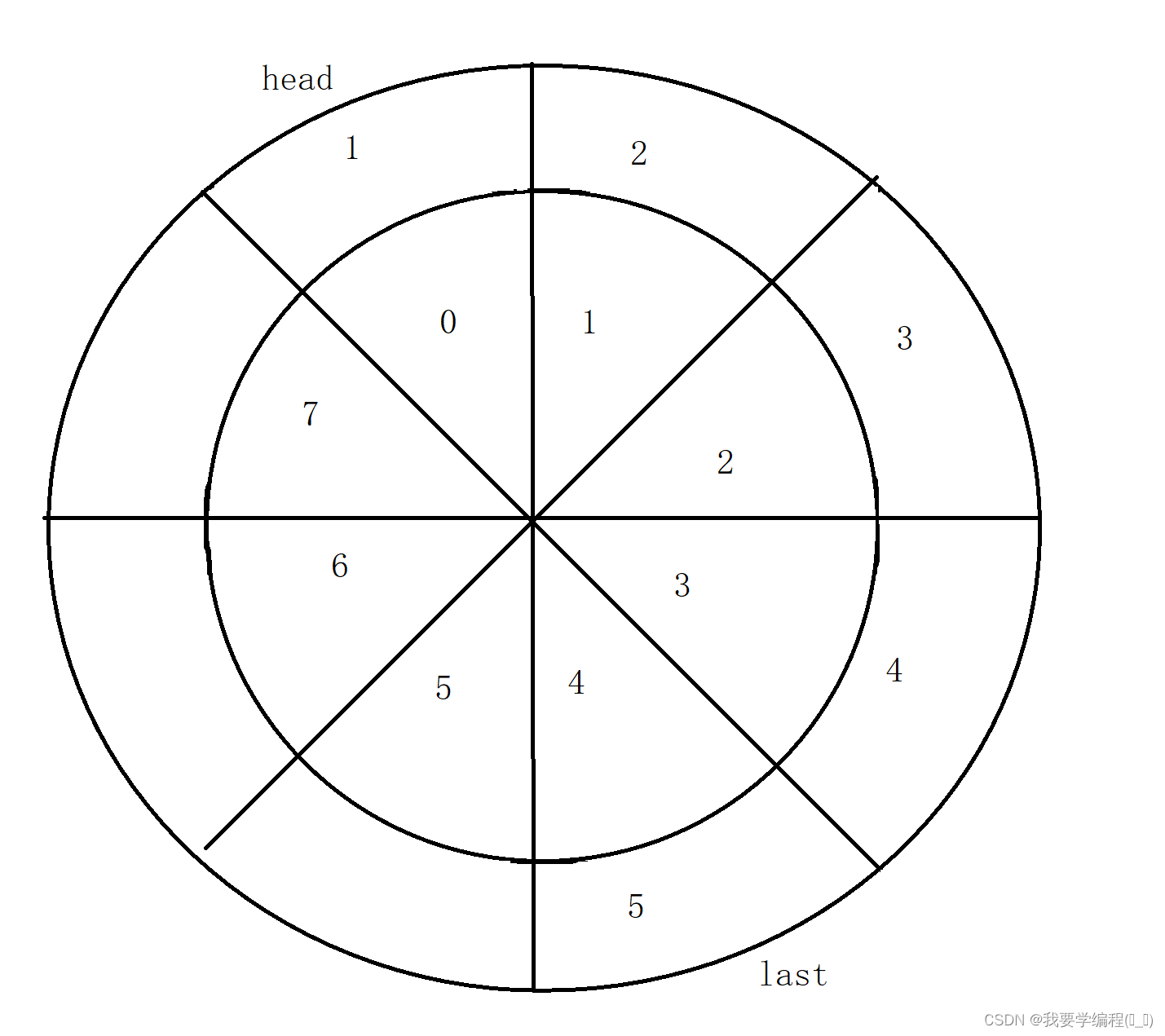
循环队列有几个要解决的难题:
1、怎么判断这个队列是空还是有元素?
可能有小伙伴会说:看head 与 last 两者的下标是否相等,如果相等,就说明队列为空;如果不相等就说明队列不为空。但是很巧不巧:当队列满了的时候,这个head 与 last 指向的位置还是一样的啊。有三种解决方案:1、使用usedSize 来记录元素的个数。当head 与 last 相遇时,看看usedSize 是否为0,不为0,就说明的确是满了;否则,就没满。2、浪费一个空间来阻止其相遇。既然当两者相遇时,不知道到底是空还是满,那我们就阻止其相遇即可,当last 的下一个位置是head时,就说明队列已经满了,则不往这个位置存放元素。3、使用标记的方式。就是通过维护一个额外的变量,来判断这个队列是否满了。例如:定义一个isEmpty的变量,初始化为true,只要执行了入队操作,就把其变为false,如果在之后的入队操作中,遇到head == last ,并且isEmpty 为false,那么就说明满了。其实这个就是排除了刚开始 head == last的情况。
2、当这个last 或者是 head 为7 时,怎么把其变为 0呢?也就是说怎么把这个下标给正常化?
大佬们给出的方法是 last = (last+1) % Queue.size();
极端情况:0 = (7+1) % 8 正常情况:1 = (0+1) % 8 、 6 = (5+1) % 8
两种难题都已经解决了,就可以开始着手写循环队列了。
622. 设计循环队列
设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
MyCircularQueue(k): 构造器,设置队列长度为 k 。Front: 从队首获取元素。如果队列为空,返回 -1 。Rear: 获取队尾元素。如果队列为空,返回 -1 。enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。isEmpty(): 检查循环队列是否为空。isFull(): 检查循环队列是否已满。示例:
MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3 circularQueue.enQueue(1); // 返回 true circularQueue.enQueue(2); // 返回 true circularQueue.enQueue(3); // 返回 true circularQueue.enQueue(4); // 返回 false,队列已满 circularQueue.Rear(); // 返回 3 circularQueue.isFull(); // 返回 true circularQueue.deQueue(); // 返回 true circularQueue.enQueue(4); // 返回 true circularQueue.Rear(); // 返回 4提示:
- 所有的值都在 0 至 1000 的范围内;
- 操作数将在 1 至 1000 的范围内;
- 请不要使用内置的队列库。
思路:其实把上面的难题解决之后,循环队列也就容易实现了。
class MyCircularQueue { // 用数组来实现循环队列 public int[] elem; // 循环数组 public int usedSize; // 记录数组的有效元素的个数 public int head; // 记录对头的位置 public int last; // 记录队尾的位置 public int lastValue; // 获取队尾的值 public MyCircularQueue(int k) { this.elem = new int[k]; } public boolean enQueue(int value) { // 如果满了,就插入失败 if (isFull()) { return false; } // 往数组中插入元素 elem[last] = value; lastValue = elem[last]; last = (last+1) % elem.length; // 注意:不能简单的++了 usedSize++; return true; } public boolean deQueue() { if (isEmpty()) { return false; } // 删除对头元素 // head 往后走就行,其余不用管 head = (head+1) % elem.length; usedSize--; return true; } public int Front() { if (isEmpty()) { return -1; } else { return elem[head]; } } public int Rear() { if (isEmpty()) { return -1; } else { return lastValue; } } public boolean isEmpty() { return usedSize == 0; } public boolean isFull() { return usedSize == elem.length; } }注意:因为这里 last 的位置会在插入元素之后发生改变, 因此,我们得把改变前的位置存起来或者把改变前的队尾值存起来,以便后面的 Rear() 方法。
这里我用的是usedSize 记录位置看是否满,也可以用其他的方法。下面是用浪费一个空间的方法:(为了更好的观察,就只给出了改动代码)
class MyCircularQueue { public MyCircularQueue(int k) { // 既然浪费了一个空间,那么我们就偷偷地多申请一个空间 this.elem = new int[k+1]; } public boolean isEmpty() { // 两者只有在队列为空时,才能相遇 return head == last; } public boolean isFull() { // 如果 last+1 == head,说明此时队列已经满了 return (last+1) % elem.length == head; } }双端队列
前面我们学习的队列都是队尾进,对头出。现在我们来学习一种全新的队列:双端队列。
双端队列(deque)是指允许两端都可以进行入队和出队操作的队列,deque 是 “double ended queue” 的简称。 那就说明元素可以从队头出队和入队,也可以从队尾出队和入队。

从上图也可以看出Deque 拓展了 Queue 的功能,并且 ArrayList 与 LinkedList 都是实现了该接口的,也就说明既有 线性的双端队列,也有链式的双端队列。
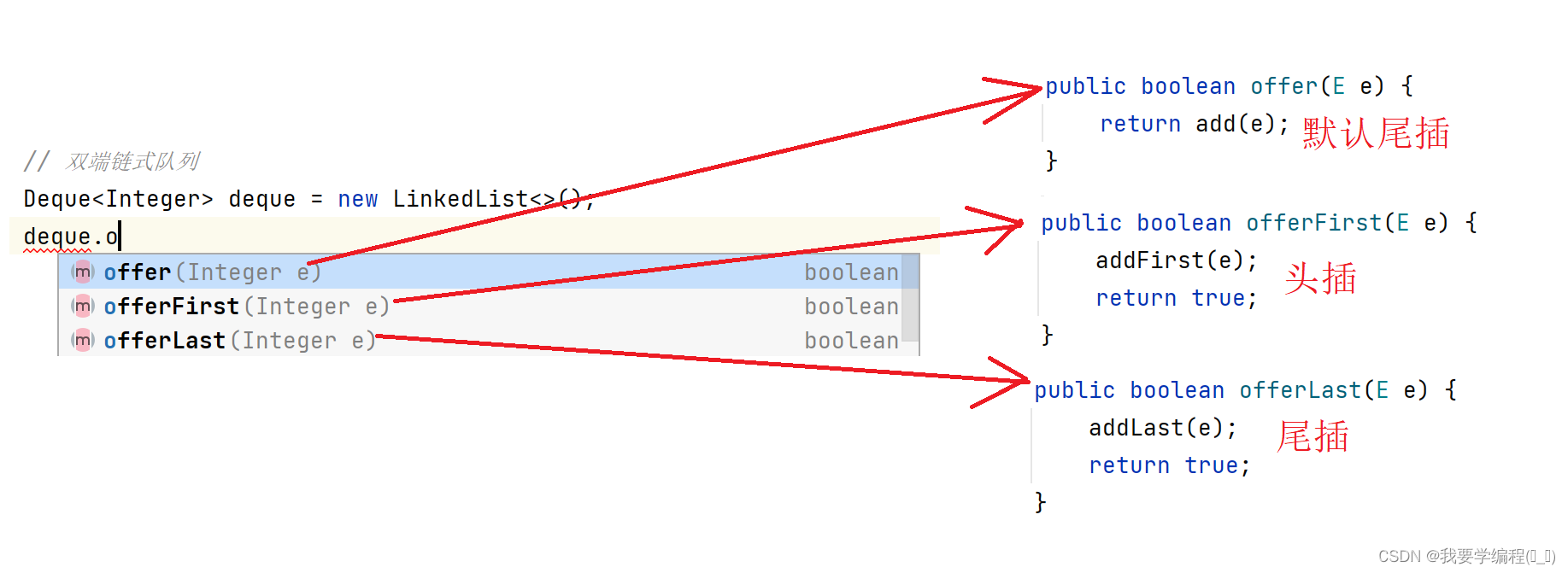
其他的方法与我们在上面的方法差不多,都是这样的,这里就不过多的赘述了。

上面是ArrayDeque 的offer() 方法。
注意:Java 8 和 Java 17 在针对ArrayDeque的无参构造方法上设计的有些不一样。

上面这个就是在浪费一个空间作为判断循环队列是否已满的情况。和我们前面的处理是一样。
由于双端队列可以在一端进,一端出,这也就表明其可以作为栈来使用了。
栈与队列相互转换
232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(
push、pop、peek、empty):实现
MyQueue类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false说明:
- 你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。- 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例 1:
输入: ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 1, 1, false] 解释: MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false提示:
1 <= x <= 9- 最多调用
100次push、pop、peek和empty- 假设所有操作都是有效的 (例如,一个空的队列不会调用
pop或者peek操作)
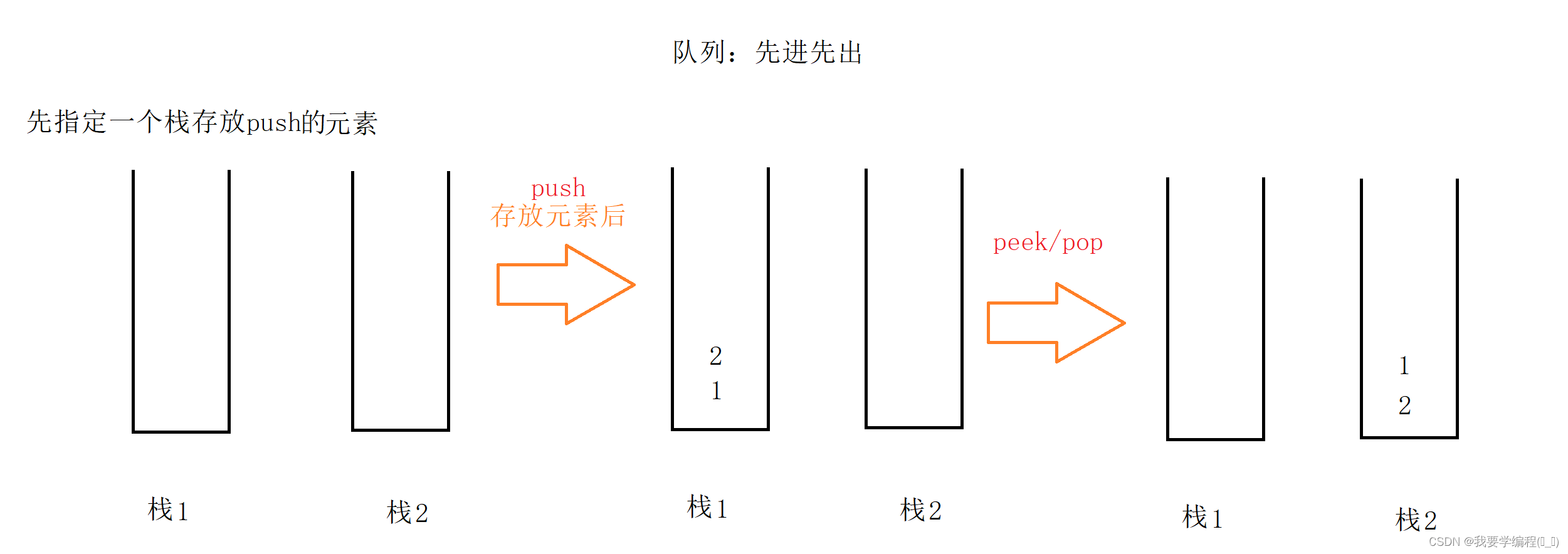
思路:先取一个栈让其作为第一次存放元素的栈, 如果进行peek 或者 pop 操作,就把有元素的栈中所有元素出栈到另一个空栈中即可,empty 就是看两个栈是否都为空。
class MyQueue { public Stack<Integer> stack1; public Stack<Integer> stack2; public MyQueue() { stack1 = new Stack<>(); stack2 = new Stack<>(); } public void push(int x) { // 如果两个栈都为空,随便选取一个作为存放元素的栈 if (empty()) { stack1.push(x); } else if (!stack1.empty()) { // 如果栈1不为空,存放到栈1中,反之则存放到栈2中 stack1.push(x); } else { stack2.push(x); } } public int pop() { // 把有元素的栈中所有元素存放到另一个栈中 if (!stack1.empty()) { int size = stack1.size(); for (int i = 0; i < size; i++) { stack2.push(stack1.pop()); } // 再颠倒过来 int x = stack2.pop(); size = stack2.size(); for (int i = 0; i < size; i++) { stack1.push(stack2.pop()); } return x; } else { int size = stack2.size(); for (int i = 0; i < size; i++) { stack1.push(stack2.pop()); } // 再颠倒过来 int x = stack2.pop(); size = stack2.size(); for (int i = 0; i < size; i++) { stack1.push(stack2.pop()); } return x; } } public int peek() { // 把有元素的栈中所有元素存放到另一个栈中 if (!stack1.empty()) { int size = stack1.size(); for (int i = 0; i < size; i++) { stack2.push(stack1.pop()); } // 再颠倒过来 // 这个peek()方法的顺序没有关系 int x = stack2.peek(); size = stack2.size(); for (int i = 0; i < size; i++) { stack1.push(stack2.pop()); } return x; } else { int size = stack2.size(); for (int i = 0; i < size; i++) { stack1.push(stack2.pop()); } // 再颠倒过来 int x = stack2.peek(); size = stack2.size(); for (int i = 0; i < size; i++) { stack1.push(stack2.pop()); } return x; } } public boolean empty() { // 当两个栈同时为空时,才为空 return stack1.empty() && stack2.empty(); } }上面这个代码有些过于繁琐了,可以简化为下面这样:
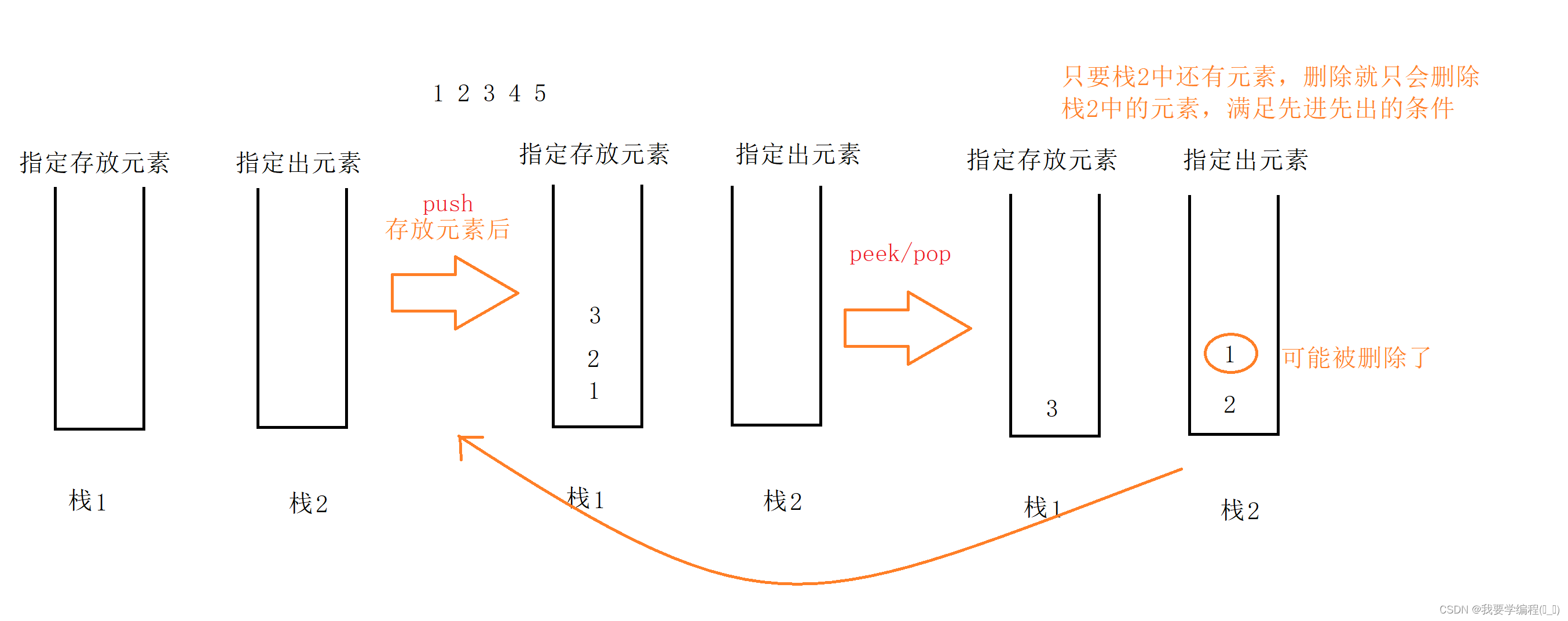
class MyQueue { public Stack<Integer> stack1; public Stack<Integer> stack2; public MyQueue() { stack1 = new Stack<>(); stack2 = new Stack<>(); } public void push(int x) { // 指定在一个中存放 stack1.push(x); } public int pop() { while (stack2.empty()) { while (!stack1.empty()) { stack2.push(stack1.pop()); } } return stack2.pop(); } public int peek() { while (stack2.empty()) { while (!stack1.empty()) { stack2.push(stack1.pop()); } } return stack2.peek(); } public boolean empty() { // 当两个栈同时为空时,才为空 return stack1.empty() && stack2.empty(); } } 这个代码就是把一个栈专门用来存放元素,另一个栈专门用来出元素。
225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(
push、top、pop和empty)。实现
MyStack类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。注意:
- 你只能使用队列的标准操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。- 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 2, 2, false] 解释: MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // 返回 2 myStack.pop(); // 返回 2 myStack.empty(); // 返回 False提示:
1 <= x <= 9- 最多调用
100次push、pop、top和empty- 每次调用
pop和top都保证栈不为空
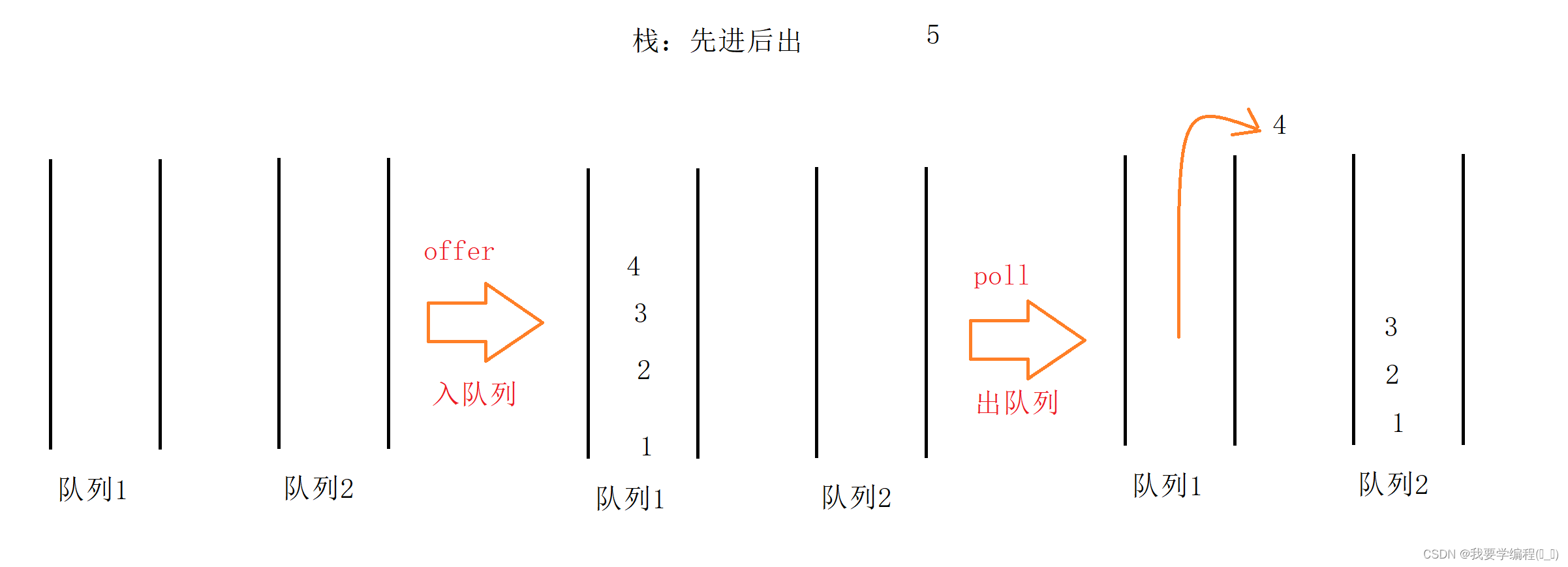
思路:一个队列存放元素,在pop时,把有元素的队列的前n-1个元素给到新队列,再根据需要处理最后一个元素即可。
class MyStack { public Queue<Integer> queue1; public Queue<Integer> queue2; public MyStack() { queue1 = new LinkedList<>(); queue2 = new LinkedList<>(); } public void push(int x) { // 如果两个都为空,则任选一个 if (!empty()) { queue1.offer(x); } else if (!queue1.isEmpty()) { queue1.offer(x); } else { queue2.offer(x); } } public int pop() { // 把不为空的队列的前n-1个元素出队 if (!queue1.isEmpty()) { int size = queue1.size(); for (int i = 0; i < size-1; i++) { queue2.offer(queue1.poll()); } // 将原队列的队尾元素出队 return queue1.poll(); } else { int size = queue2.size(); for (int i = 0; i < size-1; i++) { queue1.offer(queue2.poll()); } return queue2.poll(); } } public int top() { // 把不为空的队列的前n-1个元素出队 if (!queue1.isEmpty()) { int size = queue1.size(); for (int i = 0; i < size-1; i++) { queue2.offer(queue1.poll()); } // 得到原队列的队尾元素,并插入新队列 int x = queue1.peek(); queue2.offer(queue1.poll()); return x; } else { int size = queue2.size(); for (int i = 0; i < size-1; i++) { queue1.offer(queue2.poll()); } int x = queue2.peek(); queue1.offer(queue2.poll()); return x; } } public boolean empty() { // 两个都为空,则返回空 return queue1.isEmpty() && queue2.isEmpty(); } }当然本题可以使用双端队列,只不过题目要求要用两个队列,而且双端队列来实现栈比用两个队列更为简单,因为只需要维护一个队列即可。
双端队列 思路:创建一个双端队列,正常入队元素,但出队是从队尾出。
综上:栈与队列之间的相互转换还是不难的,只要掌握了栈与队列的特点,再根据各自的特点去实现即可。
好啦!本期 数据结构之探索“队列”的奥秘 的学习之旅就到此结束了,我们下一期再一起学习吧!
