一、问题
给你一个只包含正整数的非空数组nums。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。

二、求解思路1
动态规划解决
这题不能使用回溯算法来解决,如果数据量大的话就会超时。我们可以使用动态规划。
这题判断把数组分成两份,这两份的元素和是否相等。首先我们需要计算数组中所有元素的和sum,然后判断sum是否是偶数:如果不是偶数,说明不可能分割成完全相等的两份,直接返回false。
如 果 是 偶 数 , 我 们 只 需 要 判 断 是 否 存 在 一 些 元 素 的 和 等 于 sum/2 , 如 果 等 于sum/2,那么剩下的肯定也等于sum/2,说明我们可以把数组分为元素和相等的两部分。
那么这个时候问题就很明朗了,假设sum/2是一个背包的容量,我们只需要找出一些元素把他放到背包中,如果背包中元素的最大和等于sum/2,说明我们可以把数组分成完成相等的两份。这不就是经典的0-1背包问题吗。背包问题系列之-基础背包问题,具体可以看下,这里就不在重复介绍。我们在来找一下他的递推公式,定义dp[i][j]表示把第i个物品放到容量为j的背包中所获得的的最大值。
第i个物品的值是nums [i -1]:
如果nums [i -1]>j,说明背包容量不够,第i件物品放不进去,所以我们不能选择第i个物品,那么
dp[i][j]=dp[i -1][j];
如 果 nums [i -1]<=j , 说 明 可 以 把 第 j 个 物 品 放 到 背 包 中 , 我 们 可 以 选择放也可以选择不放,取最大值即可,如果放就会占用一部分背包容量,最大价值是
dp[i][j]=dp[i-1][j-nums[i-1]]+nums[i-1]
如果不放
dp[i][j]=dp[i -1][j];
取两者的最大值
最终递推公式和代码如下:
#include <vector> bool canPartition(std::vector<int>& nums) { // 计算数组中所有元素的和 int sum = 0; for (int num : nums) { sum += num; } // 如果sum是奇数,说明数组不可能分成完全相等的两份 if ((sum & 1) == 1) { return false; } // sum除以2 int target = sum >> 1; int length = nums.size(); std::vector<std::vector<int>> dp(length + 1, std::vector<int>(target + 1, 0)); for (int i = 1; i <= length; ++i) { for (int j = 1; j <= target; ++j) { // 下面是递推公式 if (j >= nums[i - 1]) { dp[i][j] = std::max(dp[i - 1][j], dp[i - 1][j - nums[i - 1]] + nums[i - 1]); } else { dp[i][j] = dp[i - 1][j]; } } } // 判断背包最大是否能存放和为target的元素 return dp[length][target] == target; } 我们还可以这样写,二维数组dp是boolean类型,dp[i][j]表示数组中前i个元素的和是否可以组成和为j,很明显dp[0][0]=true,表示前0个元素(也就是没有元素)可以组成和为0。代码如下
#include <vector> bool canPartition(std::vector<int>& nums) { // 计算数组中所有元素的和 int sum = 0; for (int num : nums) { sum += num; } // 如果sum是奇数,说明数组不可能分成完全相等的两份 if ((sum & 1) == 1) { return false; } // sum除以2得到target int target = sum >> 1; int length = nums.size(); std::vector<std::vector<bool>> dp(length + 1, std::vector<bool>(target + 1, false)); // base case dp[0][0] = true; for (int i = 1; i <= length; ++i) { for (int j = 0; j <= target; ++j) { // 递推公式 if (j >= nums[i - 1]) { dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]]; } else { dp[i][j] = dp[i - 1][j]; } } } // 返回能否找到和为target的子集 return dp[length][target]; } 我们看到上面二维数组计算的时候当前值只和上面一行有关,所以我们可以把它改成一维的,注意第二个for循环要倒叙,否则会把前面的值给覆盖掉导致结果错误,仔细看一下
dp[j] = (dp[j] || dp[j - nums [i - 1]]);
就明白了,相当于同一行后面的值依赖前面的,如果不是倒叙,前面的值被修改了,在计算后面的就会导致错误。我们来看下代码
#include <vector> bool canPartition(std::vector<int>& nums) { // 计算数组中所有元素的和 int sum = 0; for (int num : nums) { sum += num; } // 如果sum是奇数,说明数组不可能分成完全相等的两份 if ((sum & 1) == 1) { return false; } // sum除以2得到target int target = sum >> 1; int length = nums.size(); std::vector<bool> dp(target + 1, false); // base case dp[0] = true; for (int i = 0; i < length; ++i) { // 注意这里j要倒序 for (int j = target; j >= nums[i]; --j) { // 递推公式 dp[j] = dp[j] || dp[j - nums[i]]; } } // 返回能否找到和为target的子集 return dp[target]; } 三、求解思路2
DFS算法解决
每种元素可以选择也可以不选择,只需要判断他所有的可能组合中,元素和是否有等于sum/2的,我们可以把它看做是一棵二叉树,左子节点表示选择当前元素,右子节点表示不选择当前元素,如下图所示,橙色节点表示选择当前元素,蓝色表示不选择。
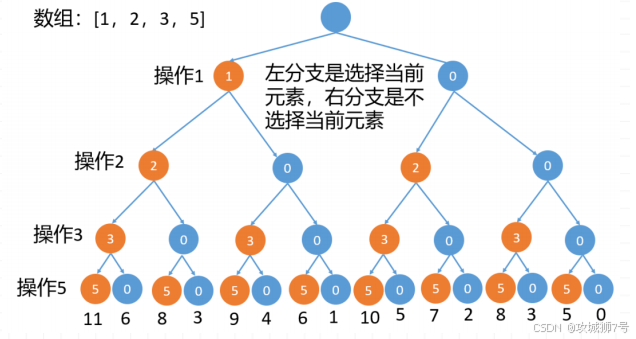
我们先看看初步实现代码
#include <vector> bool dfs(const std::vector<int>& nums, int target, int index) { // target等于0,说明存在一些元素的和等于sum/2,直接返回true if (target == 0) return true; // 如果数组元素都找完了,或者target小于0,直接返回false if (index == nums.size() || target < 0) return false; // 选择当前元素和不选择当前元素两种情况 return dfs(nums, target - nums[index], index + 1) || dfs(nums, target, index + 1); } bool canPartition(std::vector<int>& nums) { // 计算数组中所有元素的和 int sum = 0; for (int num : nums) sum += num; // 如果sum是奇数,说明数组不可能分成完全相等的两份 if ((sum & 1) == 1) return false; // 调用dfs函数 return dfs(nums, sum >> 1, 0); } 但很遗憾的是,因为计算量太大,会导致运行超时,我们可以优化一下,来看下代码
#include <vector> bool dfs(const std::vector<int>& nums, int index, int target, std::vector<std::vector<int>>& map) { // target等于0,说明存在一些元素的和等于sum/2,直接返回true if (target == 0) return true; // 如果数组元素都找完了,或者target小于0,直接返回false if (index >= nums.size() || target < 0) return false; // 如果此子问题已经被计算过,直接返回结果 if (map[index][target] != -1) return map[index][target] == 1; // 选择当前元素 bool select = dfs(nums, index + 1, target - nums[index], map); // 不选择当前元素 bool unSelect = dfs(nums, index + 1, target, map); // 存储结果,并返回 map[index][target] = select || unSelect ? 1 : 0; return select || unSelect; } bool canPartition(std::vector<int>& nums) { // 计算数组中所有元素的和 int sum = 0; for (int num : nums) sum += num; // 如果sum是奇数,说明数组不可能分成完全相等的两份 if (sum % 2 != 0) return false; // sum除以2 int target = sum / 2; std::vector<std::vector<int>> map(nums.size(), std::vector<int>(target + 1, -1)); return dfs(nums, 0, target, map); } 四、求解思路3
位运算解决
这里能使用位运算,关键在于题中的一些限制条件,比如正整数的非空数组,每个数组中的元素不会超过 100,数组的大小不会超过 200等。
原理很简单,我们只需要申请一个大小为 sum+1 的数组bits[ sum+1 ],数组中的数字只能是0和1,我们可以把它想象为一个很长的二进制位,因为int和long类型太短了,我们这里使用的是数组。然后每遍历数组中的一个元素比如m,就把二进制位往左移m位然后在和原来的二进制位进行或运算。最后判断bits[ sum/2 ]是否是1,如果是1就返回true。文字叙述不是很直接,我们就以示例1为例来画个图看一下
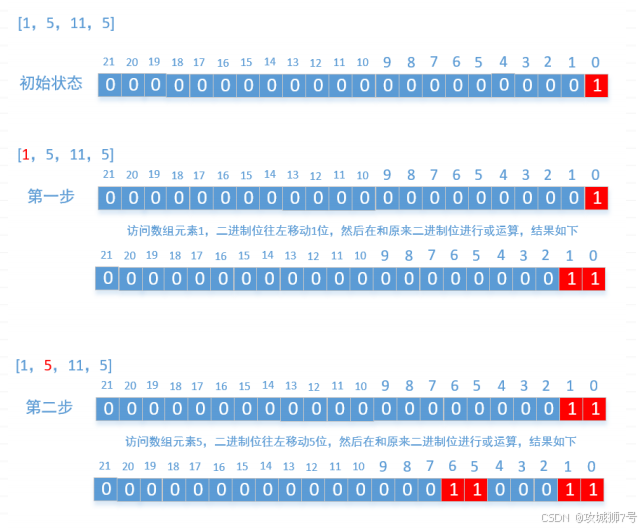
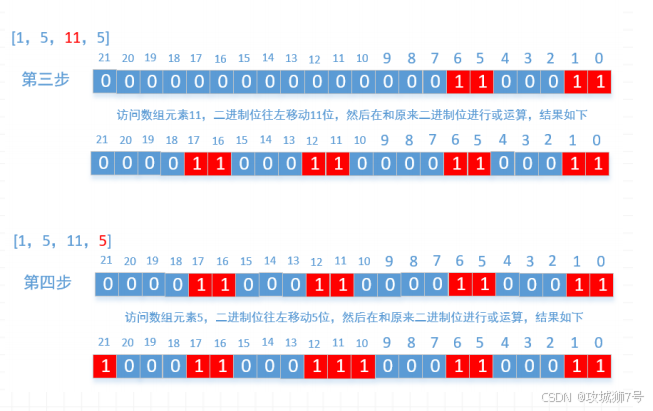
最后你会发现一个规律,就是最后运算的结果只要是1的位置,都可以使用数组中的元素组合而成,只要是0的都不能使用数组中的元素组合而成,搞懂了上面的过程,代码就很容易写了。因为我们只需要判断二进制位中中间的那个值是否为1,所以我们只需要计算低位,高位完全不用计算,因为是往左移动的,高位不会对中间的值产生任何影响,所以这里能做一点优化,最后再来看下代码。
#include <vector> bool canPartition(std::vector<int>& nums) { // 计算数组中所有数字的和 int sum = 0; for (int n : nums) { sum += n; } // 如果sum是奇数,直接返回false if ((sum & 1) == 1) { return false; } int len = sum / 2; // 这里bits的长度是len+1,因为我们只需要计算低位就行了,没必要计算所有的 std::vector<char> bits(len + 1, 0); bits[0] = 1; for (int num : nums) { for (int j = len - num; j >= 0; j--) { bits[j + num] |= bits[j]; } // 判断中位数如果是1,说明可以分成两种相等的子集,直接返回true,不需要再计算了 if ((bits[len] & 1) != 0) { return true; } } return false; } 