数学建模·Topsis优劣解&距离法

Topsis优劣解

一种新的评价方法，特点就是利用原有数据，客观性强。

相较于模糊评价和层次评价

更加客观，充分利用原有数据，精确反映方案差距

基本原理

离最优解最近，离最劣解越远

具体步骤

正向化

代码与原理与熵权法类同，不多赘述

标准化

标准化的目的是为了消除计量单位不同的影响
标准化的计算方式不是算数平均，而是平方数的平均

*优劣解打分

• 1.优先计算最优解和最劣解，作为行向量存在
  
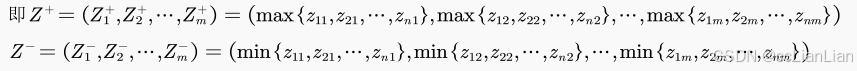
• 2.分别计算每一个对象i的j指标相对优劣解的距离
  
• 3.按照公式得出对象的得分进行归一化

带权值的优劣解计算

• 距离之差表现在矩阵乘法上作为矩阵
• 这个权值表现在矩阵乘法上是作为列向量，原因很简单：线性组合。这点很重要！
  
  w向量形式如下图
  
  公式中的"距离之差的平方"形式如下图
  

如果你运行不成功可能是变量名不一样，matlab支持一步步运行代码。

权重的计算：

熵权法/层次分析法
在需要计算时，直接跳转熵权法代码运行这一节即可(保持变量名统一)

%% 概率矩阵P、计算信息熵和熵权 P=Stand_X./repmat(sum(Stand_X),n,1); for i=1:n     for j=1:m         if P(i,j)==0             P(i,j)=0.000001         end     end end H=sum(-P.*log(P)); e=H./log(n); d=1-e; d=d./sum(d); disp("计算完成,下面是计算得出的权重矩阵"); disp(d); temp=input("是否需要正向矩阵、标准矩阵？输入1表示需要，其他表示不需要"); if temp==1     disp(X);     disp(Stand_X); end 

Topsis代码如下

%% 读取数据 X=xlsread("工作簿1.xlsx"); X=X(:,[2:5]);%注意读取时不要误读，可以直接范围所有 disp("成功读取！"); %% 正向化 disp("现在进行正向化操作，请按照提示操作") vec_col=input("请输入需要正向化的列数，以数组的形式输入\n"); for i=1:size(vec_col,2)%1是行数2是列数 flag = input(['第' num2str(vec_col(i)) '列是哪类数据(【1】:极小型 【2】：中间型 【3】：区间型)，请输入序号：\n']);     if flag==1         X(:,vec_col(i))=Min2Max(X(:,vec_col(i)));     elseif flag==2         best=input("请你传入最佳值\n");         X(:,vec_col(i))=Mid2Max(X(:,vec_col(i)),best);     else         arr=input("请你输入区间的左右端点，以数组的形式\n");         X(:,vec_col(i))=Interval2Max(X(:,vec_col(i)),arr(1),arr(2));     end end disp("正向化完成！"); %% 标准化 [n,m]=size(X); Square_X=X.*X; Sum_X=sum(Square_X).^0.5; Stand_X=X./repmat(Sum_X,n,1); disp("标准化完成！") %% 优劣解打分 min_X=min(Stand_X,[],1);%[C,index] = max(A,[],dim); max_X=max(Stand_X,[],1); disp("正在使用优劣解打分"); temp=ones(m); weight=temp(:,1);%默认权值 need_w_flag=input("是否需要手动输入权值？如果需要请输入1\n"); if need_w_flag==1     weight=input("请将权值以列的形式给出！"); end Z_plus=repmat(max_X,n,1); Z_sub=repmat(min_X,n,1); D_plus=sum((Z_plus-Stand_X).^2*weight,2).^2; %根据公式weight一定要右乘 D_sub=sum((Z_sub-Stand_X).^2*weight,2).^2; S=D_sub./(D_sub+D_plus); %归一化 S=S./sum(S); disp("评分如下"); disp(S); xlswrite("工作簿1.xlsx",S,'F2:F26'); 

距离法

基本原理

根据每一个元素与最大值最小值的距离打分，比较朴素，一般不使用这个方法评

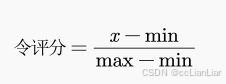
代码如下

%% 读取数据 X=xlsread("工作簿1.xlsx"); X=X(:,[2:5]);%注意读取时不要误读，可以直接范围所有 disp("成功读取！"); %% 正向化 disp("现在进行正向化操作，请按照提示操作") vec_col=input("请输入需要正向化的列数，以数组的形式输入\n"); for i=1:size(vec_col,2)%1是行数2是列数 flag = input(['第' num2str(vec_col(i)) '列是哪类数据(【1】:极小型 【2】：中间型 【3】：区间型)，请输入序号：\n']);     if flag==1         X(:,vec_col(i))=Min2Max(X(:,vec_col(i)));     elseif flag==2         best=input("请你传入最佳值\n");         X(:,vec_col(i))=Mid2Max(X(:,vec_col(i)),best);     else         arr=input("请你输入区间的左右端点，以数组的形式\n");         X(:,vec_col(i))=Interval2Max(X(:,vec_col(i)),arr(1),arr(2));     end end disp("正向化完成！"); %% 标准化 [n,m]=size(X); Square_X=X.*X; Sum_X=sum(Square_X).^0.5; Stand_X=X./repmat(Sum_X,n,1); disp("标准化完成！") %% 距离法打分 min_X=min(Stand_X,[],1);%[C,index] = max(A,[],dim); max_X=max(Stand_X,[],1); res1=(Stand_X-repmat(min_X,n,1))./(repmat(max_X,n,1)-repmat(min_X,n,1)); disp(res1);